UR3机器人运动学分析之逆运动学分析_ur3运动学

前往我的博客阅读体验更佳：本文链接

2 逆运动学分析

  逆运动学就是已知末端执行器相对于基坐标系的位置和姿态，求对应的六个关节角度。设末端执行器相对于基坐标系的位姿矩阵为：
T 6 0 = [ n x o x a x p x n y o y a y p y n z o z a z p z 0 0 0 1 ] (1) T^0_6 =

$$\begin{bmatrix} n_x & o_x & a_x & p_x \\ n_y & o_y & a_y & p_y \\ n_z & o_z & a_z & p_z \\ 0 & 0 & 0 & 1 \end{bmatrix}$$ \tag{1} T60​= ​nx​ny​nz​0​ox​oy​oz​0​ax​ay​az​0​px​py​pz​1​ ​(1)

2.1 逆运动学求解

2.1.1 关节1的求解

已知
T 6 0 = [ n x o x a x p x n y o y a y p y n z o z a z p z 0 0 0 1 ] = T 1 0 ⋅ T 2 1 ⋅ T 3 2 ⋅ T 4 3 ⋅ T 5 4 ⋅ T 6 5 (2) T^0_6 =

$$\begin{bmatrix} n_x & o_x & a_x & p_x \\ n_y & o_y & a_y & p_y \\ n_z & o_z & a_z & p_z \\ 0 & 0 & 0 & 1 \end{bmatrix}$$ =T^0_1·T^1_2·T^2_3·T^3_4·T^4_5·T^5_6 \tag{2} T60​= ​nx​ny​nz​0​ox​oy​oz​0​ax​ay​az​0​px​py​pz​1​ ​=T10​⋅T21​⋅T32​⋅T43​⋅T54​⋅T65​(2)
将式(2)两边分别左乘$(T_1^0{)}^{-1}$和右乘$(T_6^5{)}^{-1}$，有：
$$(T_1^0{)}^{-1}\ast T_6^0\ast (T_6^5{)}^{-1}=T_2^1\cdot T_3^2\cdot T_4^3\cdot T_5^4\text{\hspace{1em}(3)}$$
因为：
$$(T_1^0{)}^{-1}=\left[\begin{array}{cccc}{c}_1& s_1& 0& 0\\ -s_1& c_1& 0& 0\\ 0& 0& 1& -d_1\\ 0& 0& 0& 1\end{array}\right]\text{\hspace{1em}(4)}$$

( T 6 5 ) − 1 = [ c 6 0 − s 6 0 − s 6 0 − c 6 0 0 1 0 − d 6 0 0 0 1 ] (5) (T^5_6)^{-1} =

$$\begin{bmatrix} c_6 & 0 & -s_6 & 0 \\ -s_6 & 0 & -c_6 & 0 \\ 0 & 1 & 0 & -d_6 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$ \tag{5} (T65​)−1= ​c6​−s6​00​0010​−s6​−c6​00​00−d6​1​ ​(5)

所以有：
( T 1 0 ) − 1 ∗ T 6 0 ∗ ( T 6 5 ) − 1 = [ q 11 q 12 q 13 q 14 q 21 q 22 q 23 q 24 q 31 q 32 q 33 q 34 0 0 0 1 ] (6) (T^0_1)^{-1}*T^0_6*(T^5_6)^{-1}=

$$\begin{bmatrix} q_{11} & q_{12} & q_{13} & q_{14} \\ q_{21} & q_{22} & q_{23} & q_{24} \\ q_{31} & q_{32} & q_{33} & q_{34} \\ 0 & 0 & 0 & 1 \end{bmatrix}$$ \tag{6} (T10​)−1∗T60​∗(T65​)−1= ​q11​q21​q31​0​q12​q22​q32​0​q13​q23​q33​0​q14​q24​q34​1​ ​(6)
式(6)中，各简式分别为：
$$\{\begin{array}{l}{q}_{11}=c_6(c_1{n}_x+s_1{n}_y)-s_6(c_1{o}_x+s_1{o}_y)\\ q_{12}=c_1{a}_x+s_1{a}_y\\ q_{13}=-c_6(c_1{o}_x+s_1{o}_y)-s_6(c_1{n}_x+s_1{n}_y)\\ q_{14}=c_1{p}_x+s_1{p}_y-(c_1{a}_x+s_1{a}_y)d_6\\ q_{21}=c_6(c_1{n}_y-s_1{n}_x)-s_6(c_1{o}_y-s_1{o}_x)\\ q_{22}=c_1{a}_y-s_1{a}_x\\ q_{23}=c_6(s_1{o}_x-c_1{o}_y)-s_6(c_1{n}_y-s_1{n}_x)\\ q_{24}=c_1{p}_y-s_1{p}_x+d_6(s_1{a}_x-c_1{a}_y)\\ q_{31}=c_6{n}_z-s_6{o}_z\\ q_{32}=a_z\\ q_{33}=-s_6{n}_z-c_6{o}_z\\ q_{34}=p_z-d_1-a_z{d}_6\end{array}\text{\hspace{1em}(7)}$$
而式(3)右边结果为：
$$T_2^1\cdot T_3^2\cdot T_4^3\cdot T_5^4=\left[\begin{array}{cccc}{c}_{234}{c}_5& -c_{234}{s}_5& s_{234}& c_{23}{a}_3+c_2{a}_2+s_{234}{d}_5\\ -s_5& -c_5& 0& -d_2-d_4\\ s_{234}{c}_5& -s_{234}{s}_5& -c_{234}& s_{23}{a}_3+s_2{a}_2-c_{234}{d}_5\\ 0& 0& 0& 1\end{array}\right]\text{\hspace{1em}(8)}$$
由式(6)和式(8)第二行第四列元素相等，可以得到：
$$\begin{array}{rl}-d_2-d_4& =c_1{p}_y-s_1{p}_x+d_6(s_1{a}_x-c_1{a}_y)\\ & =(p_y-a_y{d}_6)c_1-(p_x-a_x{d}_6)s_1\end{array}\text{\hspace{1em}(9)}$$
令$m=p_y-a_y{d}_6,n=p_x-a_x{d}_6$，则式(9)可化为：
$$m{c}_1-n{s}_1=-d_2-d_4\text{\hspace{1em}(10)}$$
利用辅助角公式可将上式化为：
$$\sqrt{m^2+n^2}\sin (\phi -{\theta }_1)=-d_2-d_4\text{\hspace{1em}(11)}$$
即：
$$\sin (\phi -{\theta }_1)=\frac{-d_2-d_4}{\sqrt{m^2+n^2}}\text{\hspace{1em}(12)}$$
其中，$\sin (\phi )=\frac{m}{\sqrt{m^2+n^2}}$，$\cos (\phi )=\frac{n}{\sqrt{m^2+n^2}}$，则：
$$\phi =Atan2(m,n)\text{\hspace{1em}(13)}$$
由式(12)可得：
$$\cos (\phi -{\theta }_1)=\pm \sqrt{1-(\frac{-d_2-d_4}{\sqrt{m^2+n^2}}{)}^2}\text{\hspace{1em}(14)}$$
由式(12)和式(14)可得：
$$\phi -{\theta }_1=Atan2(-d_2-d_4,\pm \sqrt{m^2+n^2-(d_2+d_4{)}^2})\text{\hspace{1em}(15)}$$
即：
$${\theta }_1=\phi -Atan2(-d_2-d_4,\pm \sqrt{m^2+n^2-(d_2+d_4{)}^2})\text{\hspace{1em}(16)}$$
将式(13)代入上式可求得${\theta }_1$：
$${\theta }_1=Atan2(m,n)-Atan2(-d_2-d_4,\pm \sqrt{m^2+n^2-(d_2+d_4{)}^2})\text{\hspace{1em}(17)}$$

共两个解。

2.1.2 关节5的求解

由式(6)和式(8)第二行第二列元素相等，可以得到：
$$-c_5=c_1{a}_y-s_1{a}_x\text{\hspace{1em}(18)}$$
由于${\theta }_1$已知，则可求得${\theta }_5$为：
$${\theta }_5=\pm \arccos (s_1{a}_x-c_1{a}_y)\text{\hspace{1em}(19)}$$
共两个解。

2.1.3 关节6的求解

由式(6)和式(8)第二行第一列元素相等，可以得到：
$$-s_5=c_6(c_1{n}_y-s_1{n}_x)-s_6(c_1{o}_y-s_1{o}_x)\text{\hspace{1em}(20)}$$
由式(6)和式(8)第二行第三列元素相等，可以得到：
$$0=c_6(s_1{o}_x-c_1{o}_y)-s_6(c_1{n}_y-s_1{n}_x)\text{\hspace{1em}(21)}$$
令$s=c_1{n}_y-s_1{n}_x$，$t=c_1{o}_y-s_1{o}_x$，式(20)和式(21)可写成：
$$s{c}_6-t{s}_6=-s_5\text{\hspace{1em}(22)}$$
$$s{s}_6+t{c}_6=0\text{\hspace{1em}(23)}$$
当$s_5\ne 0$时，将式(22)和式(23)两边平方后相加，可得：
$$s^2+t^2=s_5^2\text{\hspace{1em}(24)}$$
由于式(22)和式(10)形式类似，因此，可得到${\theta }_6$：
θ 6 = A t a n 2 ( s , t ) − A t a n 2 ( − s 5 , ± s 2 + t 2 − s 5 2 ) = A t a n 2 ( s , t ) − A t a n 2 ( − s 5 , 0 ) (25)

$$\begin{aligned} \theta_6 & =\mathrm{Atan2}(s,t)-\mathrm{Atan2}(-s_5,\pm\sqrt{s^2+t^2-s_5^2}) \\ & =\mathrm{Atan2}(s,t)-\mathrm{Atan2}(-s_5,0) \end{aligned}$$ \tag{25} θ6​​=Atan2(s,t)−Atan2(−s5​,±s2+t2−s52​ ​)=Atan2(s,t)−Atan2(−s5​,0)​(25)

共一个解。

若$s_5=0$，此时机器人处于奇异位置。

2.1.4 关节3的求解

对式(3)两边同时右乘$(T_5^4{)}^{-1}$可得：
$$(T_1^0{)}^{-1}\ast T_6^0\ast (T_6^5{)}^{-1}\cdot (T_5^4{)}^{-1}=T_2^1\cdot T_3^2\cdot T_4^3\text{\hspace{1em}(26)}$$
因为$(T_5^4{)}^{-1}$为：
( T 5 4 ) − 1 = [ c 5 0 s 5 0 − s 5 0 c 5 0 0 − 1 0 − d 5 0 0 0 1 ] (27) (T^4_5)^{-1} =

$$\begin{bmatrix} c_5 & 0 & s_5 & 0 \\ -s_5 & 0 & c_5 & 0 \\ 0 & -1 & 0 & -d_5 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$ \tag{27} (T54​)−1= ​c5​−s5​00​00−10​s5​c5​00​00−d5​1​ ​(27)
所以式(26)左边为：
$$(T_1^0{)}^{-1}\ast T_6^0\ast (T_6^5{)}^{-1}\ast (T_5^4{)}^{-1}=\left[\begin{array}{cccc}{r}_{11}& r_{12}& r_{13}& r_{14}\\ r_{21}& r_{22}& r_{23}& r_{24}\\ r_{31}& r_{32}& r_{33}& r_{34}\\ 0& 0& 0& 1\end{array}\right]\text{\hspace{1em}(28)}$$
式(28)中部分简式如下：
$$\{\begin{array}{l}{r}_{14}=c_1{p}_x+s_1{p}_y-d_6(s_1{a}_y+c_1{a}_x)+d_5[c_6(c_1{o}_x+s_1{o}_y)+s_6(c_1{n}_x+s_1{n}_y)]\\ r_{34}=p_z-d_1-a_z{d}_6+d_5(s_6{n}_z+c_6{o}_z)\end{array}\text{\hspace{1em}(29)}$$

由于下述计算过程并未使用矩阵中其它元素，故此处未给出。

式(26)右边为：
T 2 1 ⋅ T 3 2 ⋅ T 4 3 = [ c 234 − s 234 0 c 23 a 3 + c 2 a 2 0 0 − 1 − d 2 − d 4 s 234 c 234 0 s 23 a 3 + s 2 a 2 0 0 0 1 ] (30) T^1_2·T^2_3·T^3_4=

$$\begin{bmatrix} c_{234} & -s_{234} & 0 & c_{23}a_3+c_2a_2 \\ 0 & 0 & -1 & -d_2-d_4 \\ s_{234} & c_{234} & 0 & s_{23}a_3+s_2a_2 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$ \tag{30} T21​⋅T32​⋅T43​= ​c234​0s234​0​−s234​0c234​0​0−100​c23​a3​+c2​a2​−d2​−d4​s23​a3​+s2​a2​1​ ​(30)
由式(28)和式(30)第一行第四列元素和第三行第四列元素分别相等，得：
$$\{\begin{array}{l}{a}_3{c}_{23}+a_2{c}_2=r_{14}\\ a_3{s}_{23}+a_2{s}_2=r_{34}\end{array}\text{\hspace{1em}(31)}$$
两边平方后相加得到：
$$a_3^2+a_2^2+2a_2{a}_3(c_{23}{c}_2+s_{23}{s}_2)=r_{14}^2+r_{34}^2\text{\hspace{1em}(32)}$$
注意到$c_{23}{c}_2+s_{23}{s}_2=\cos ({\theta }_2+{\theta }_3)\cos ({\theta }_2)+\sin ({\theta }_2+{\theta }_3)\sin ({\theta }_2)=\cos ({\theta }_2+{\theta }_3-{\theta }_2)=\cos ({\theta }_3)$.
所以${\theta }_3$为：
$${\theta }_3=\pm \arccos (\frac{r_{14}^2+r_{34}^2-a_3^2-a_2^2}{2a_2{a}_3})\text{\hspace{1em}(33)}$$

共两个解。

2.1.5 关节2的求解

利用三角函数公式，方程组式(31)可以化为：
{ ( a 3 c 3 + a 2 ) s 2 + a 3 s 3 c 2 = r 14 − a 3 s 3 s 2 + ( a 3 c 3 + a 2 ) c 2 = r 34 (34) \left\{

$$\begin{array}{lr} (a_3c_3+a_2)s_2+a_3s_3c_2 = r_{14} \\ -a_3s_3s_2+(a_3c_3+a_2)c_2 = r_{34} \end{array}$$ \right.\tag{34} {(a3​c3​+a2​)s2​+a3​s3​c2​=r14​−a3​s3​s2​+(a3​c3​+a2​)c2​=r34​​(34)
求解方程组式(34)，结果如下：
$$\{\begin{array}{l}{s}_2=\frac{(a_3{c}_3+a_2)r_{34}-a_3{s}_3{r}_{14}}{a_3^2+a_2^2+2a_2{a}_3{c}_3}\\ c_2=\frac{a_3{s}_3{r}_{34}+(a_3{c}_3+a_2)r_{14}}{a_3^2+a_2^2+2a_2{a}_3{c}_3}\end{array}\text{\hspace{1em}(35)}$$
则${\theta }_2$为：
$${\theta }_2=Atan2(s_2,c_2)\text{\hspace{1em}(36)}$$

共一个解。

2.1.6 关节4的求解

由式(6)和式(8)第一行第三列元素和第三行第三列元素分别相等，可以得到：
{ s 234 = − s 6 ( c 1 n x + s 1 n y ) − c 6 ( c 1 o x + s 1 o y ) c 234 = s 6 n z + c 6 o z (37) \left\{

$$\begin{array}{lr} s_{234}=-s_6(c_1n_x+s_1n_y)-c_6(c_1o_x+s_1o_y) \\ c_{234}=s_6n_z+c_6o_z \end{array}$$ \right.\tag{37} {s234​=−s6​(c1​nx​+s1​ny​)−c6​(c1​ox​+s1​oy​)c234​=s6​nz​+c6​oz​​(37)
则${\theta }_4$为：
$${\theta }_4=Atan2(s_{234},c_{234})-{\theta }_2-{\theta }_3\text{\hspace{1em}(38)}$$
共一个解。

2.1.7 总结

综上所述，可以得到六个关节角的解析解表达式如下：
$${\theta }_1=Atan2(m,n)-Atan2(-d_2-d_4,\pm \sqrt{m^2+n^2-(d_2+d_4{)}^2})\text{\hspace{1em}(39)}$$
其中，$m=p_y-a_y{d}_6$，$n=p_x-a_x{d}_6$。
$${\theta }_5=\pm \arccos (s_1{a}_x-c_1{a}_y)\text{\hspace{1em}(40)}$$
$${\theta }_6=Atan2(s,t)-Atan2(-s_5,0)\text{\hspace{1em}(41)}$$
其中，$s=c_1{n}_y-s_1{n}_x$，$t=c_1{o}_y-s_1{o}_x$。
$${\theta }_3=\pm \arccos (\frac{r_{14}^2+r_{34}^2-a_3^2-a_2^2}{2a_2{a}_3})\text{\hspace{1em}(42)}$$
其中，$r_{14}=c_1{p}_x+s_1{p}_y-d_6(s_1{a}_y+c_1{a}_x)+d_5[c_6(c_1{o}_x+s_1{o}_y)+s_6(c_1{n}_x+s_1{n}_y)]$，$r_{34}=p_z-d_1-a_z{d}_6+d_5(s_6{n}_z+c_6{o}_z)$。
$${\theta }_2=Atan2(s_2,c_2)\text{\hspace{1em}(43)}$$
其中，$s_2=\frac{(a_3{c}_3+a_2)r_{34}-a_3{s}_3{r}_{14}}{a_3^2+a_2^2+2a_2{a}_3{c}_3}$，$c_2=\frac{a_3{s}_3{r}_{34}+(a_3{c}_3+a_2)r_{14}}{a_3^2+a_2^2+2a_2{a}_3{c}_3}$。
$${\theta }_4=Atan2(s_{234},c_{234})-{\theta }_2-{\theta }_3\text{\hspace{1em}(44)}$$

其中，$s_{234}=-s_6(c_1{n}_x+s_1{n}_y)-c_6(c_1{o}_x+s_1{o}_y)$，$c_{234}=-s_6{n}_z-c_6{o}_z$。

  在上述求解公式中，由于${\theta }_1$、${\theta }_5$、${\theta }_3$存在“$\pm$”号的影响，所以该机器人对同一种末端位姿可能存在八组解。

2.2 程序编写

  在2.1.7节中已经给出各个关节角的解析解表达式，利用表达式编写逆运动学求解程序，由于UR3机器人位姿表示方法采用旋转矢量形式，因此程序有齐次变换矩阵及旋转矢量两种输入方式，程序流程图如下图所示。

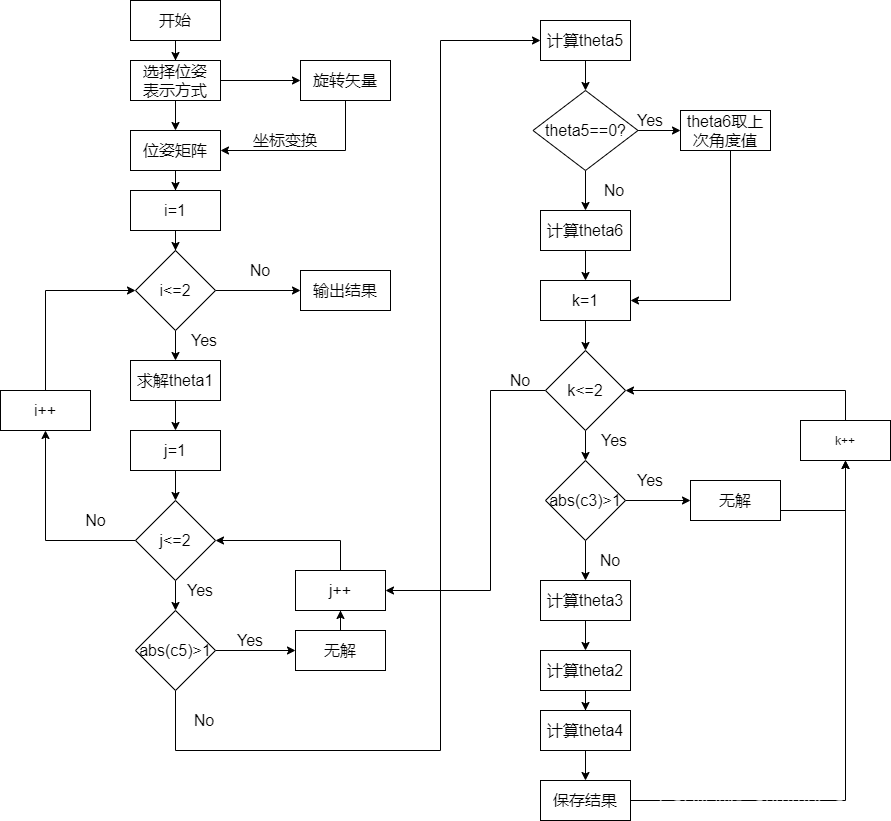
  注意到求解${\theta }_5$的表达式为：
$${\theta }_5=\pm \arccos (s_1{a}_x-c_1{a}_y)\text{\hspace{1em}(45)}$$
如果
$$|\cos {\theta }_5|=|s_1{a}_x-c_1{a}_y|>1\text{\hspace{1em}(46)}$$

但是余弦函数的值域为$[-1,1]$，所以式(46)无意义，这种情况下解不存在。同理，求解${\theta }_3$时也存在同样的问题。也就是说，八组解析解并不一定全都存在。

  同时，由于计算机内部存储数据类型的原因，当求解出的角度为零时实际存储的数值并不一定是零，由于误差的累计，后面角度的求解结果会产生较大的偏差，因此在每个角度求解完毕后需要添加如下程序块进行手动判零：

if abs(theta_5) < eps
	theta_5 = 0;
end
1
2
3

2.3 验证

  采用正逆运动学相互求解的方法验证解的正确与否。首先利用正运动学求得关节角为$\Theta ={\left[15^{\circ }15^{\circ }15^{\circ }15^{\circ }15^{\circ }15^{\circ }\right]}^T$时的位姿矩阵为：
T 6 0 = [ 0.5252 − 0.8478 0.0732 − 313.9360 − 0.1181 − 0.1578 − 0.9804 − 280.8134 0.8428 0.5062 − 0.1830 − 91.7142 0 0 0 1.0000 ] (47) T^0_6=

$$\begin{bmatrix} 0.5252 & -0.8478 & 0.0732 & -313.9360 \\ -0.1181 & -0.1578 & -0.9804 & -280.8134 \\ 0.8428 & 0.5062 & -0.1830 & -91.7142 \\ 0 & 0 & 0 & 1.0000 \end{bmatrix}$$ \tag{47} T60​= ​0.5252−0.11810.84280​−0.8478−0.15780.50620​0.0732−0.9804−0.18300​−313.9360−280.8134−91.71421.0000​ ​(47)
  利用上述位姿矩阵进行逆运动学求解，求得八组解如下所示:

  分别将每一组解利用正运动学计算位姿矩阵，发现得到的位姿矩阵同初始位姿矩阵相同，证明逆运动学解析解表达式无误。