当前位置: article > 正文

智能反射面| 宽带情况的智能反射面信道估计——arxiv上的最新paper阅读笔记_智能反射面接收的信号表示

作者：Cpp五条 | 2024-05-05 19:00:00

踩

智能反射面接收的信号表示

原文标题：Broadband Channel Estimation for Intelligent
Reflecting Surface Aided mmWave Massive MIMO Systems
地址： https://arxiv.org/pdf/2002.01629.pdf

前言：智能反射面的工作中，个人认为信道估计举足轻重。因为其他的诸如波束成形的设计等，都基于较好的CSI（信道信息）前提下。最近arxiv上，信道估计的文章也开始如雨后春笋冒出，之所以挑这篇文章在疫情期间写，是因为这是我看到的第一篇考虑了宽带情形的信道估计——众所周知，在毫米波信道假设下，宽带才是更合理的场景。

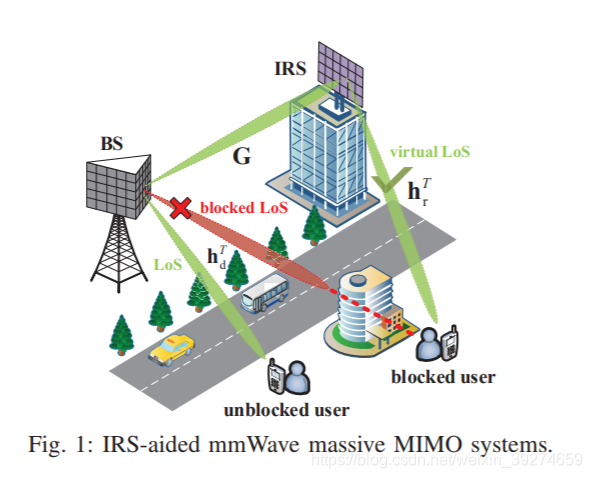
在这里插入图片描述

系统与信道模型

本文考虑的场景如上图所示，即通过智能发射面，使得一些直射路径被障碍物遮蔽的用户，可以接收到反射的信号来改善通信。

这篇文章考虑的信道模型主要有两个特点：

考虑了毫米波信道的稀疏性。即多径数是有限的。有些paper里假设的是瑞利或者莱斯信道，这里是有区别的。
考虑了宽带情况，即各径之间是有时延差的。

要估计的信道，其实分为2个路径， 3个部分

基站直接到用户的信道： $h_d$
基站通过反射面到用户：分为基站-反射面： $G$ , 反射面-用户： $h_r$

信道建模方面，文章选用了最常见的模型:
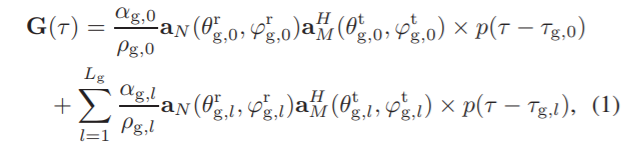
在这里插入图片描述
右边的第一项代表了主径（LOS径），第二项代表了多条非主径(NLOS)径的叠加。作者考虑的是基站与智能反射面均为UPA的情形。因此，式子里也有 $\theta$ 和 $\phi$ ，即俯角和仰角。具体就不展开了，这是最标准的毫米波S-V信道模型。

需要注意的是相比于窄带系统，每一项后面都乘上了一个 $p$ ，代表信道的时延。

文章假设了使用OFDM系统，也就是说将上述的信道再写成子载波信道的形式如下：

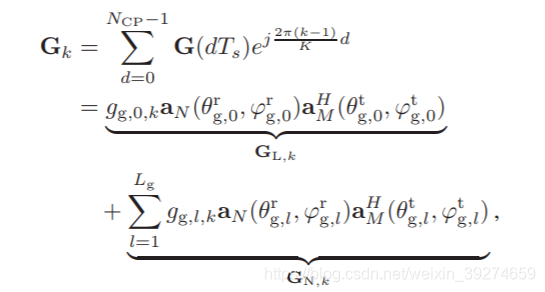
在这里插入图片描述
相同的推导可以得到 $h_d$ 和 $h_r$ ，不再赘述。

一个重要假设

文章中提出了一个全文至关重要的假设：基站-反射面之间的信道，可以认为是已知的。

这一点非常关键。首先，由于智能反射面默认不配备RF chain，因此是无法做信道估计的。许多其他文献往往智能将基站-反射面信道与反射面-用户的信道合并估计，但显然大大增加了复杂度，降低了准确度。如果这一假设成立的话，问题会变得容易很多，因为最难估计的一部分可以认为是已知的。

作者紧接着解释了这一假设的合理性。其实核心就是一点： 基站与智能反射面通常是固定的。 与用户随时可能移动不同，基站和智能反射面之间的信道，一般是固定不变的。同时，由于LOS径可以由基站与只能反射面的空间几何关系算出，完全可以认为是可以先验得到。而NLOS径的能量则可以认为远远小于LOS径，可以建模为高斯噪声。

在这一假设下，问题就变得简单了很多，即只需估计 $h_d$ 和 $h_r$ 。

估计方法

文章考虑的是下行估计。第 $i$ 时刻，用户端接收到的信号可以表示为：
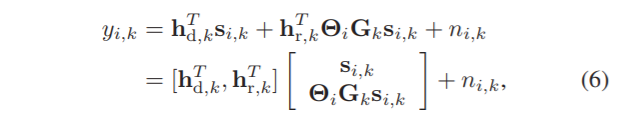
在这里插入图片描述
右边第一行的第一项代表直射路径的到达信号，第二项是经过智能反射面反射得到的信号。其中，

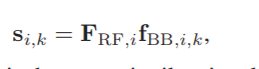
这里可能默认发送的pilot的信号为1.

考虑连续发 $N_p$ 个信号，可以表示为：
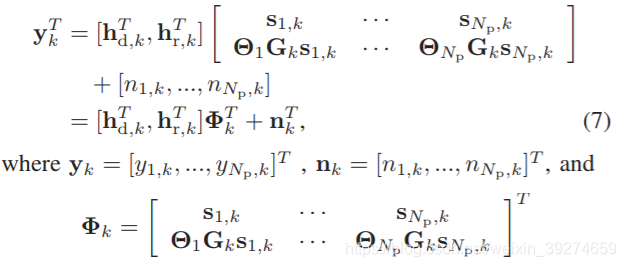
在这里插入图片描述
这里和学长讨论后，认为这个假设其实有点牵强。因为他假设了BS-IRS的信道是LOS dominated，但是在后续的估计IRS-UE中，又没有了这个假设，还是按多径来估计。

压缩感知

在前面的信道模型中，已经提到，作者假设信道是稀疏的。而一种最常见的求解方法就是利用压缩感知。

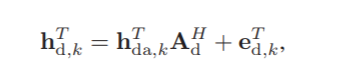
在这里插入图片描述

$A_d$ 是一个冗余的字典矩阵， $h_{da}$ 则是一个稀疏向量，其非零值就代表了真实存在的信道的径。由于毫米波的稀疏性，非零值也就较少，因此是稀疏向量。 $e_d$ 代表量化误差。因为字典矩阵是离散的，而真实的信道角度是连续的，因此会有误差。这也是压缩感知方法的通病。具体的压缩感知的知识可以自行百度，也可以参看我们之前的几篇博客中，毫米波信道使用压缩感知估计。

DOMP （ distributed orthogonal matching pursuit）

需要注意的是，与普通的窄带压缩感知估计不同，宽带情况下，有K个子载波都需要估计，但需要满足一个条件：
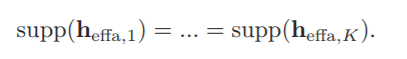
在这里插入图片描述
这个式子的意思就是，所有子载波信道其实都是由稀疏的时域信道变换得来，也就是说其支撑集是一致的——所有子载波信道所对应的稀疏向量中非零值的位置是一致的，但非零值可能是不等的。

因此，作者提出了DOMP算法，和OMP算法唯一的区别其实是在第三步：

在这里插入图片描述
即在求解时将所有子载波的相关值加和起来计算。

码字的设计

本文的重心不在于码字的设计，作者直接选用了恒1的数字波束成形和随机生成的模拟波束成形与智能反射面反射因子。理论上是有优化空间的。

字典的设计

作者提出使用高分辨率字典，即字典数大于天线数。这一点我之前也考虑过，理论上字典做的越细，即码字数量越多，那么分辨率就会越高，性能也会越好。

仿真

作者最后展示了一下性能。因为这个题材很新，尤其是宽带的估计，因此对比算法非常少，就简单的与LS算法进行了对比。

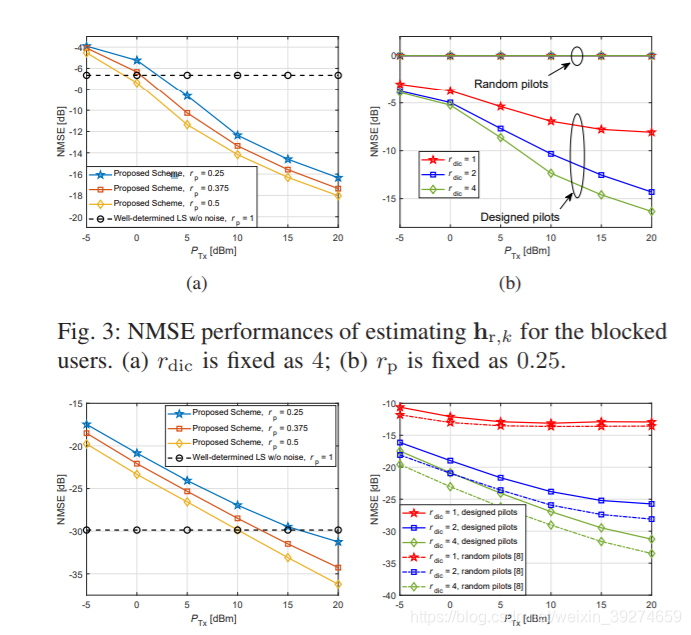
在这里插入图片描述

总体而言这篇文章还是给予了一些启发的。

总结

本文的几个亮点

考虑了宽带稀疏信道模型
假设了BS-IRS（基站-反射面）的信道先验已知
使用了DOMP算法来求解宽带信道估计问题

智能反射面| 宽带情况的智能反射面信道估计——arxiv上的最新paper阅读笔记_智能反射面接收的信号表示

系统与信道模型

一个重要假设

估计方法

压缩感知

DOMP （ distributed orthogonal matching pursuit）

码字的设计

字典的设计

仿真

总结

相关阅读