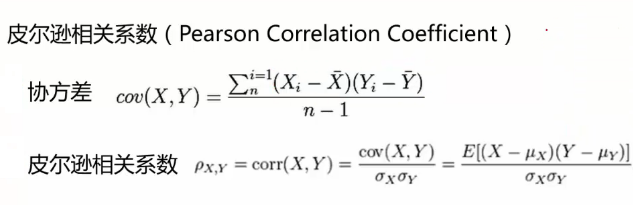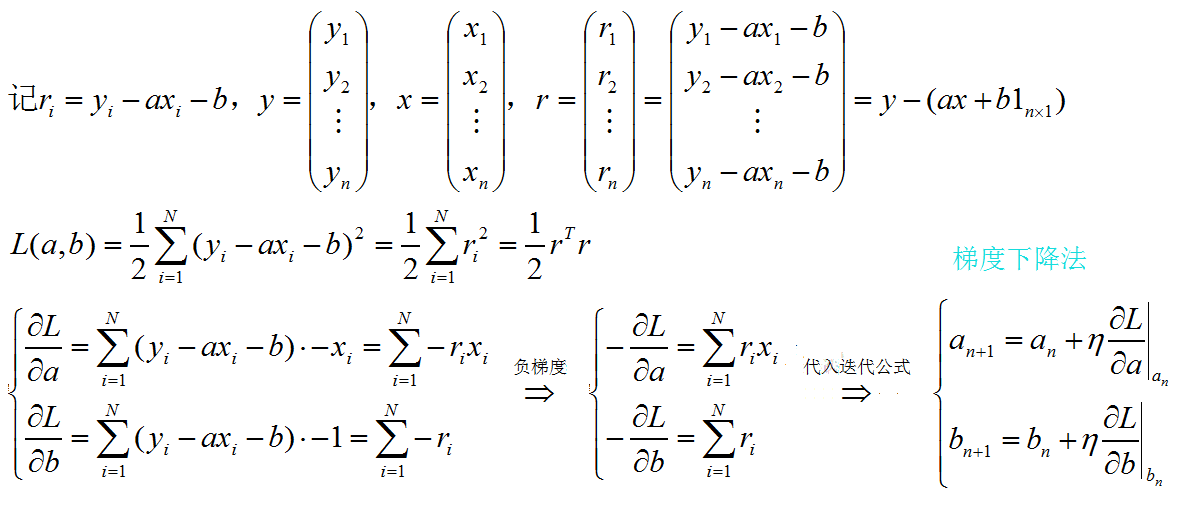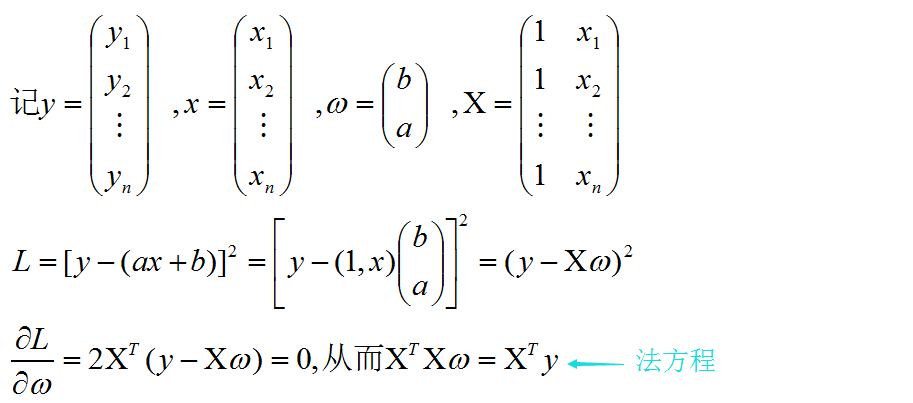Python机器学习库sklearn几种回归算法建模及分析(实验)_sklearn中都有哪些回归算法regression

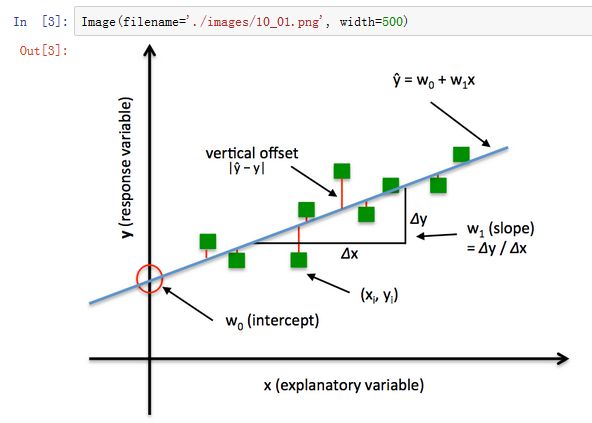
最简单的回归模型就是线性回归

数据导入与可视化分析

from IPython.display import Image
%matplotlib inline
# Added version check for recent scikit-learn 0.18 checks
from distutils.version import LooseVersion as Version
from sklearn import __version__ as sklearn_version

#原数据网址变了，新换的数据地址需要处理http://lib.stat.cmu.edu/datasets/boston
import pandas as pd
import numpy as np
#df = pd.read_csv('http://lib.stat.cmu.edu/datasets/boston',header=19,sep='\s{1,3}')
#df.head()
dfnp=np.genfromtxt('boston.txt')
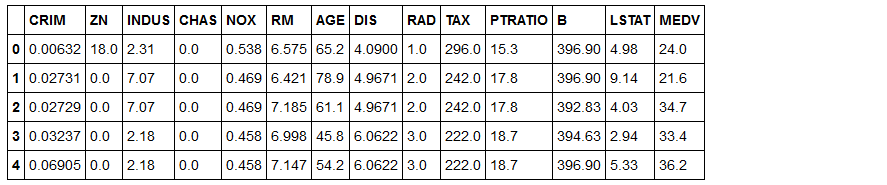
df=pd.DataFrame(dfnp,columns = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV'])
df.to_csv('boston.csv')
df.head()

import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='whitegrid', context='notebook')   #style控制默认样式,context控制着默认的画幅大小
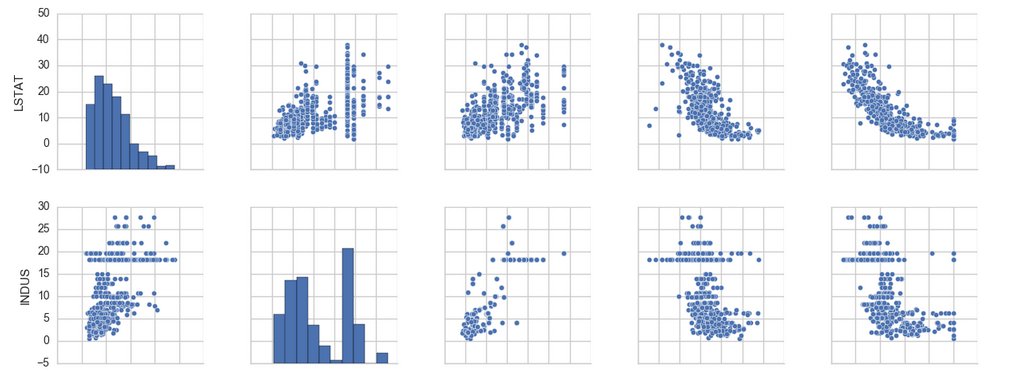
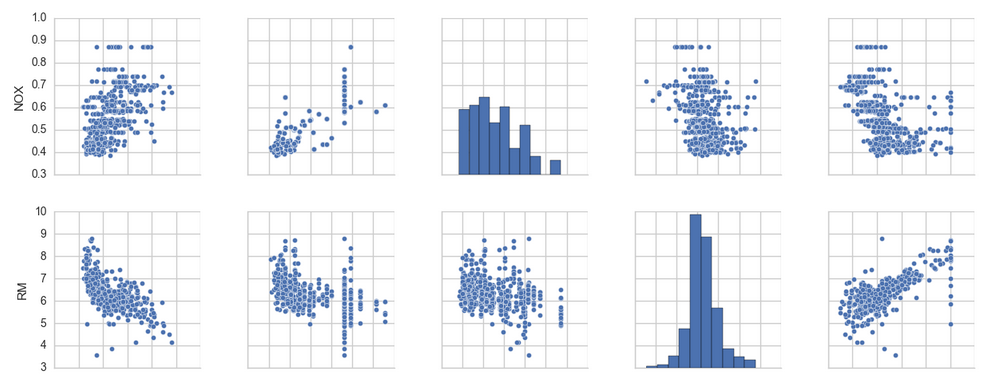
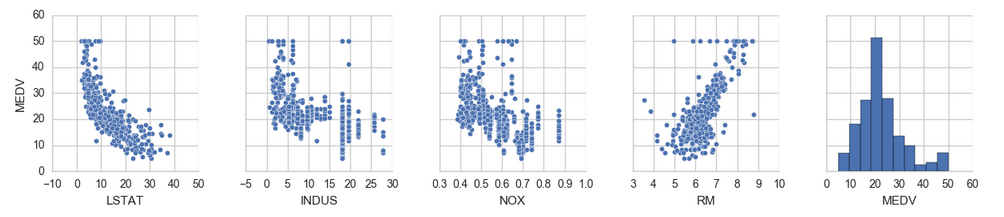
cols = ['LSTAT', 'INDUS', 'NOX', 'RM', 'MEDV']
sns.pairplot(df[cols], size=2.5)
plt.tight_layout()
# plt.savefig('./figures/scatter.png', dpi=300)
plt.show()

import numpy as np
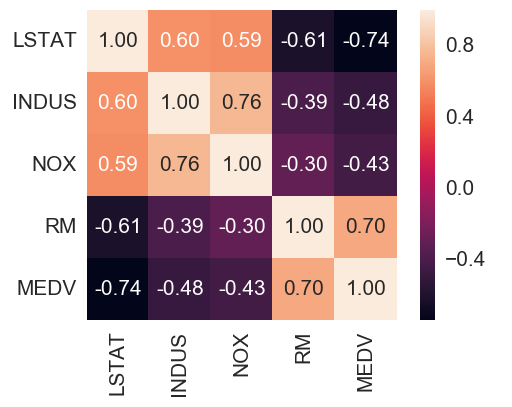
cm = np.corrcoef(df[cols].values.T)   #corrcoef方法按行计算皮尔逊相关系数,cm是对称矩阵
#使用np.corrcoef(a)可计算行与行之间的相关系数,np.corrcoef(a,rowvar=0)用于计算各列之间的相关系数,输出为相关系数矩阵。
sns.set(font_scale=1.5)   #font_scale设置字体大小
hm = sns.heatmap(cm,cbar=True,annot=True,square=True,fmt='.2f',annot_kws={'size': 15},yticklabels=cols,xticklabels=cols)
# plt.tight_layout()
# plt.savefig('./figures/corr_mat.png', dpi=300)
plt.show()

sns.reset_orig()   #将参数还原为seaborn作图前的原始值
%matplotlib inline

线性回归的最小二乘法

#编制最小二乘法类
class LinearRegressionGD(object):
    def __init__(self, eta=0.001, n_iter=20):
        self.eta = eta
        self.n_iter = n_iter
    def fit(self, X, y):   #X是列向量,y是行向量
        self.w_ = np.zeros(1 + X.shape[1])   #初始化(1,2)全0的行向量,存迭代过程拟合直线的两个系数
        self.cost_ = []
        for i in range(self.n_iter):
            output = self.net_input(X)
            errors = (y - output)   #与y同维度的行向量,errors是误差项
            self.w_[1:] += self.eta * X.T.dot(errors)   #拟合直线的一次项系数
            self.w_[0] += self.eta * errors.sum()   #拟合直线的常数项
            cost = (errors**2).sum() / 2.0   #残差的平方和一半——目标函数
            self.cost_.append(cost)
        return self
    def net_input(self, X):
        return np.dot(X, self.w_[1:]) + self.w_[0]   
    def predict(self, X):
        return self.net_input(X)
#cost_是每次迭代的残差平方和一半的统计列表，w_包含每次迭代直线的两个参数，errors是每次迭代的残差

X = df[['RM']].values   #X是(*,1)维列向量
y = df['MEDV'].values   #y是(*, )行向量
from sklearn.preprocessing import StandardScaler
sc_x = StandardScaler()
sc_y = StandardScaler()
X_std = sc_x.fit_transform(X)   
#fit_transform方法可以拆分成StanderdScalar里的fit和transform两步,这里为了区别LinearRegressionGD类将两步合并
y_std = sc_y.fit_transform(y[:, np.newaxis]).flatten()   
#y[:, np.newaxis]作用等同于y[np.newaxis].T,也就是df[['MEDV']].values；flatten方法的作用是变回成1*n的向量
#fit_transform方法是对“列向量”直接规范化
lr = LinearRegressionGD()
lr.fit(X_std, y_std)   #这里的fit是LinearRegressionGD类的,注意区分sklearn里不同类的fit方法使用环境
#Output:<__main__.LinearRegressionGD at 0x16add278>
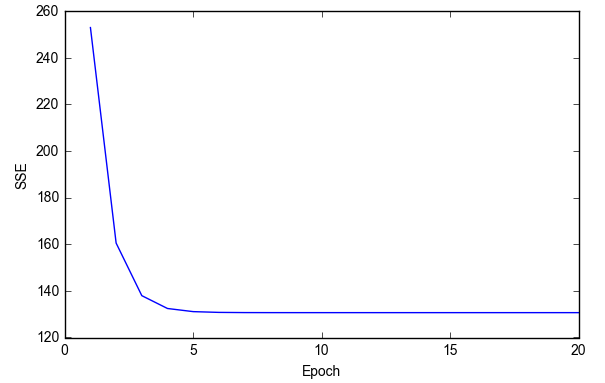
plt.plot(range(1, lr.n_iter+1), lr.cost_)
plt.ylabel('SSE')
plt.xlabel('Epoch')
plt.tight_layout()
# plt.savefig('./figures/cost.png', dpi=300)
plt.show()

def lin_regplot(X, y, model):
    plt.scatter(X, y, c='lightblue')
    plt.plot(X, model.predict(X), color='red', linewidth=2)    
    return 

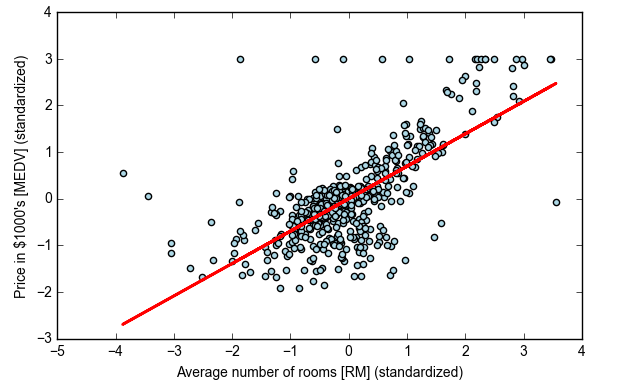
lin_regplot(X_std, y_std, lr)
plt.xlabel('Average number of rooms [RM] (standardized)')
plt.ylabel('Price in $1000\'s [MEDV] (standardized)')
plt.tight_layout()
# plt.savefig('./figures/gradient_fit.png', dpi=300)
plt.show()

print('Slope: %.3f' % lr.w_[1])   #ax+b里的a
print('Intercept: %.3f' % lr.w_[0])   #ax+b里的b
#Output:
#Slope: 0.695
#Intercept: -0.000
num_rooms_std = sc_x.transform(np.array([[5.0]]))   #与建模时数据进行同样的标准化转化
price_std = lr.predict(num_rooms_std)   #a*num_rooms_std+b
print("Price in $1000's: %.3f" % sc_y.inverse_transform(price_std))
#Output:
#Price in $1000's: 10.840

#用sklearn完成回归并查看系数，与上面自己编写的LinearRegressionGD对比
from sklearn.linear_model import LinearRegression
slr = LinearRegression()
slr.fit(X, y)
y_pred = slr.predict(X)
print('Slope: %.3f' % slr.coef_[0])
print('Intercept: %.3f' % slr.intercept_)
#Output:
#Slope: 9.102
#Intercept: -34.671
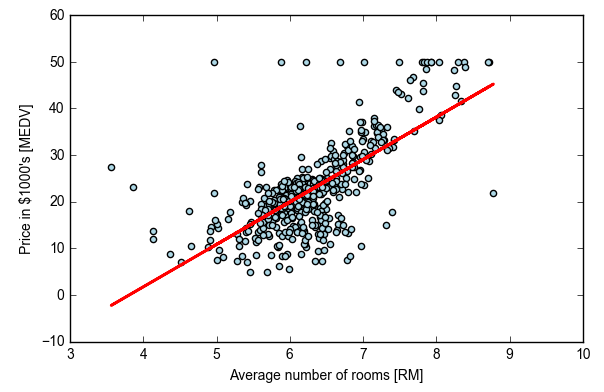
lin_regplot(X, y, slr)
plt.xlabel('Average number of rooms [RM]')
plt.ylabel('Price in $1000\'s [MEDV]')
plt.tight_layout()
# plt.savefig('./figures/scikit_lr_fit.png', dpi=300)
plt.show()

下面利用法方程求解拟合直线系数

# adding a column vector of "ones"
Xb = np.hstack((np.ones((X.shape[0], 1)), X))   #在X前加一列1
w = np.zeros(X.shape[1])
z = np.linalg.inv(np.dot(Xb.T, Xb))   
#np.linalg.inv方法利用线性代数包求逆，np.dot(Xb.T, Xb)是2*2方阵
w = np.dot(z, np.dot(Xb.T, y))
 
print('Slope: %.3f' % w[1])
print('Intercept: %.3f' % w[0])
#Output:
#Slope: 9.102
#Intercept: -34.671
#从上面结果可见:Logistic Regression求拟合直线的原理就是利用法方程

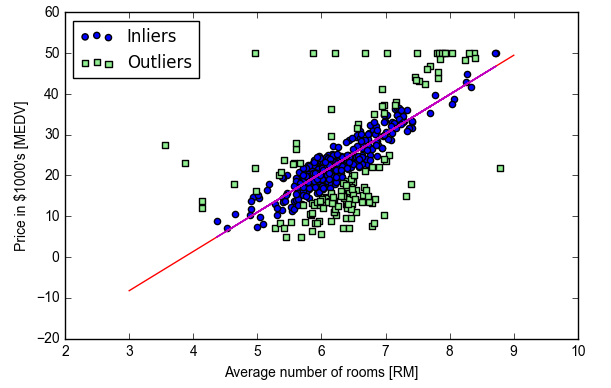
使用sklearn的RANSAC提高鲁棒性

去除噪声点，利用完全数据的有效内点子集做回归a subset of inliers（对应outliers是离群点）

from sklearn.linear_model import RANSACRegressor
#http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.RANSACRegressor.html#sklearn.linear_model.RANSACRegressor
#RANSACRegressor是从样本总体中随机取无噪声子集，回归拟合直线
if Version(sklearn_version) < '0.18':
    ransac = RANSACRegressor(LinearRegression(), max_trials=100, min_samples=50, 
                             residual_metric=lambda x: np.sum(np.abs(x), axis=1), 
                             residual_threshold=5.0, random_state=0)
else:
    ransac = RANSACRegressor(LinearRegression(), max_trials=100, min_samples=50, 
                             loss='absolute_loss', residual_threshold=5.0, random_state=0)
#base_estimator基本估计器对象默认为LR，max_trials随机样本子集选择的最大迭代次数，
#min_samples最少需要取样的点数，loss是样本损失判定准则，residual_threshold是检测离群点的样本损失阈值
ransac.fit(X, y)
inlier_mask = ransac.inlier_mask_   #将ransac对象的inliers标注为True
outlier_mask = np.logical_not(inlier_mask)   #取非，numpy库里避免python本身含有的not重载
 
line_X = np.arange(3, 10, 1)
line_y_ransac = ransac.predict(line_X[:, np.newaxis])   #构造出的验证ransac预测点
 
plt.scatter(X[inlier_mask], y[inlier_mask], c='blue', marker='o', label='Inliers')
plt.scatter(X[outlier_mask], y[outlier_mask], c='lightgreen', marker='s', label='Outliers')
 
plt.plot(line_X, line_y_ransac, color='red')   #构造出的预测点做的回归线
plt.plot(X[inlier_mask],ransac.predict(X[inlier_mask]),color='m')   #用于建模的inliers点做的回归线
plt.xlabel('Average number of rooms [RM]')
plt.ylabel('Price in $1000\'s [MEDV]')
plt.legend(loc='upper left')
 
plt.tight_layout()
# plt.savefig('./figures/ransac_fit.png', dpi=300)
plt.show()

print('Slope: %.3f' % ransac.estimator_.coef_[0])
print('Intercept: %.3f' % ransac.estimator_.intercept_)
#Output:
#Slope: 9.621
#Intercept: -37.137

评估回归模型的性能

if Version(sklearn_version) < '0.18':
    from sklearn.cross_validation import train_test_split
else:
    from sklearn.model_selection import train_test_split
 
X = df.iloc[:, :-1].values   #除去最后一列,其余都作为特征考虑范围
y = df['MEDV'].values
 
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
slr = LinearRegression()
slr.fit(X_train, y_train)
y_train_pred = slr.predict(X_train)
y_test_pred = slr.predict(X_test)
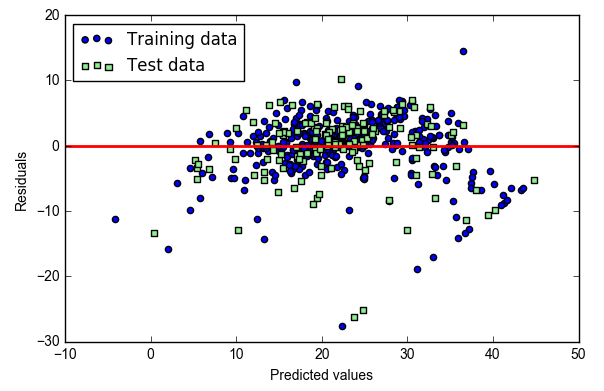
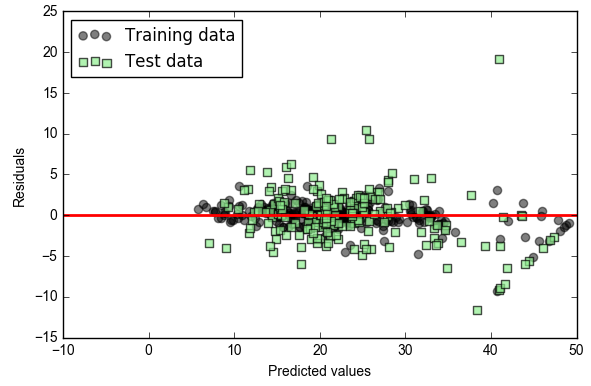
plt.scatter(y_train_pred, y_train_pred - y_train, c='blue', marker='o', label='Training data')
plt.scatter(y_test_pred, y_test_pred - y_test, c='lightgreen', marker='s', label='Test data')
#预测值与偏差的关系
plt.xlabel('Predicted values')
plt.ylabel('Residuals')
plt.legend(loc='upper left')
plt.hlines(y=0, xmin=-10, xmax=50, lw=2, color='red')
plt.xlim([-10, 50])
plt.tight_layout()
# plt.savefig('./figures/slr_residuals.png', dpi=300)
plt.show()

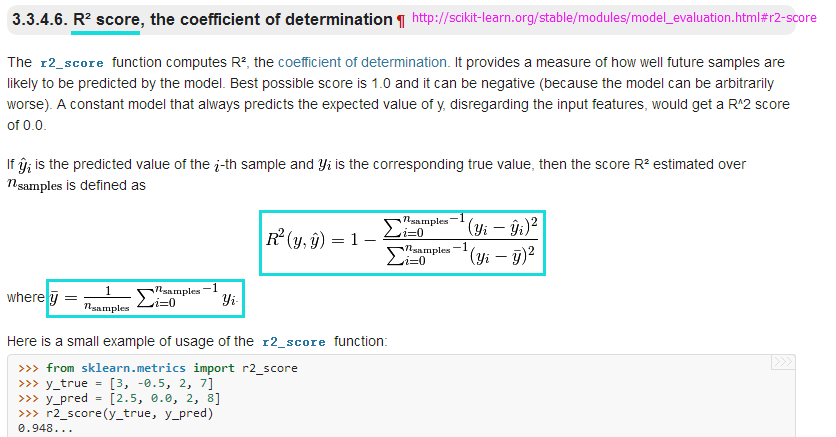
from sklearn.metrics import r2_score
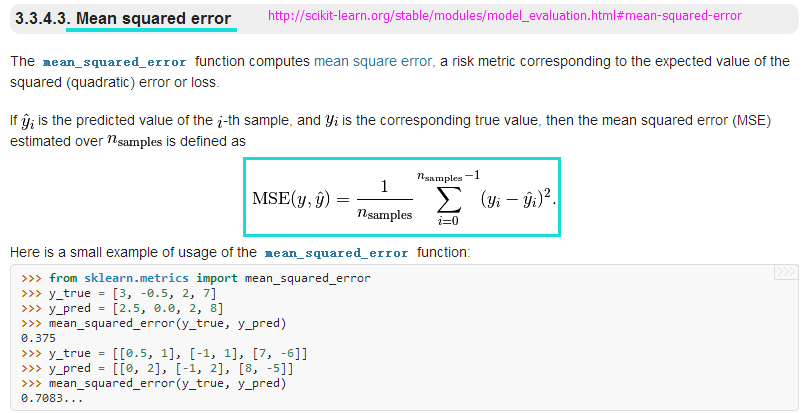
from sklearn.metrics import mean_squared_error   #均方误差回归损失
#http://scikit-learn.org/stable/modules/generated/sklearn.metrics.mean_squared_error.html#sklearn.metrics.mean_squared_error
print('MSE train: %.3f, test: %.3f' % (mean_squared_error(y_train, y_train_pred),mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (r2_score(y_train, y_train_pred),r2_score(y_test, y_test_pred)))
#Output:
#MSE train: 19.958, test: 27.196
#R^2 train: 0.765, test: 0.673

添加正则化项

from sklearn.linear_model import Lasso
#http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Lasso.html#sklearn.linear_model.Lasso
lasso = Lasso(alpha=0.1)   #L1正则化系数
lasso.fit(X_train, y_train)
y_train_pred = lasso.predict(X_train)
y_test_pred = lasso.predict(X_test)
print(lasso.coef_)
print('MSE train: %.3f, test: %.3f' % (mean_squared_error(y_train, y_train_pred),mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (r2_score(y_train, y_train_pred),r2_score(y_test, y_test_pred)))
#Output:
#[-0.11311792  0.04725111 -0.03992527  0.96478874 -0.          3.72289616
# -0.02143106 -1.23370405  0.20469    -0.0129439  -0.85269025  0.00795847
# -0.52392362]
#MSE train: 20.926, test: 28.876
#R^2 train: 0.753, test: 0.653

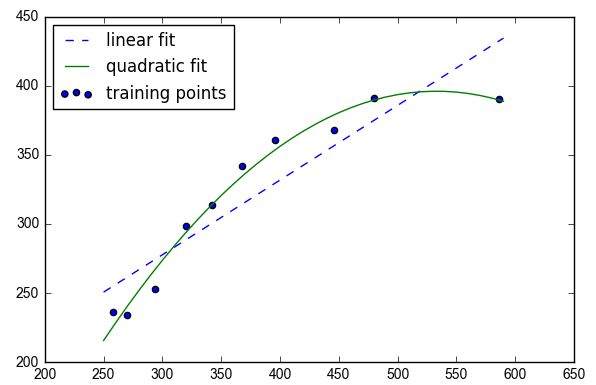
多项式回归与曲线拟合

X = np.array([258.0, 270.0, 294.0, 320.0, 342.0, 368.0, 396.0, 446.0, 480.0, 586.0])[:, np.newaxis]
y = np.array([236.4, 234.4, 252.8, 298.6, 314.2, 342.2, 360.8, 368.0, 391.2, 390.8])
from sklearn.preprocessing import PolynomialFeatures   #生成多项式特征,不是直接用多项式模型拟合
#http://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.PolynomialFeatures.html#sklearn.preprocessing.PolynomialFeatures
lr = LinearRegression()
pr = LinearRegression()
quadratic = PolynomialFeatures(degree=2)   #degress设置多项式拟合中多项式的最高次数
X_quad = quadratic.fit_transform(X)   #X列向量，fit_transform是对X按列求[1, X, X^2]，即构造二次项数据
#For example, if an input sample is two dimensional and of the form [a, b], the degree-2 polynomial features are [1, a, b, a^2, ab, b^2].
# fit linear features
lr.fit(X, y)
X_fit = np.arange(250, 600, 10)[:, np.newaxis]   #X_fit是构造的预测数据,X是训练数据
y_lin_fit = lr.predict(X_fit)   #利用线性回归对构造的X_fit数据预测
 
# fit quadratic features
pr.fit(X_quad, y)   #X_quad是训练数据,使用它进行建模得多项式系数
y_quad_fit = pr.predict(quadratic.fit_transform(X_fit))   #利用二次多项式对构造的X_fit数据预测
 
# plot results
plt.scatter(X, y, label='training points')
plt.plot(X_fit, y_lin_fit, label='linear fit', linestyle='--')
plt.plot(X_fit, y_quad_fit, label='quadratic fit')
plt.legend(loc='upper left')
 
plt.tight_layout()
# plt.savefig('./figures/poly_example.png', dpi=300)
plt.show()

#验证pr.fit(X_quad, y)可以借助LinearRegression类中的判定边界构造部分求多项式系数
pr.fit(X_quad, y)
pr.coef_
#Output:
#array([  0.00000000e+00,   2.39893018e+00,  -2.25020109e-03])
y_lin_pred = lr.predict(X)   #用训练数据集训练的线性模型，对训练数据集进行线性预测(因为线性模型建模时,就不是100%学习到了精确模型)
y_quad_pred = pr.predict(X_quad)
print('Training MSE linear: %.3f, quadratic: %.3f' % (mean_squared_error(y, y_lin_pred),mean_squared_error(y, y_quad_pred)))
print('Training R^2 linear: %.3f, quadratic: %.3f' % (r2_score(y, y_lin_pred),r2_score(y, y_quad_pred)))
#Output:
#Training MSE linear: 569.780, quadratic: 61.330
#Training R^2 linear: 0.832, quadratic: 0.982

X = df[['LSTAT']].values
y = df['MEDV'].values
regr = LinearRegression()
# create quadratic features
quadratic = PolynomialFeatures(degree=2)
cubic = PolynomialFeatures(degree=3)
X_quad = quadratic.fit_transform(X)
X_cubic = cubic.fit_transform(X)
# fit features
X_fit = np.arange(X.min(), X.max(), 1)[:, np.newaxis]
 
regr = regr.fit(X, y)   #X,y训练数据集建模；X_fit测试数据集预测；对训练数据集测试得分(因为有时根本不知道测试数据集对应的真实y值)
y_lin_fit = regr.predict(X_fit)
linear_r2 = r2_score(y, regr.predict(X))
 
regr = regr.fit(X_quad, y)
y_quad_fit = regr.predict(quadratic.fit_transform(X_fit))
quadratic_r2 = r2_score(y, regr.predict(X_quad))
 
regr = regr.fit(X_cubic, y)
y_cubic_fit = regr.predict(cubic.fit_transform(X_fit))
cubic_r2 = r2_score(y, regr.predict(X_cubic))
 
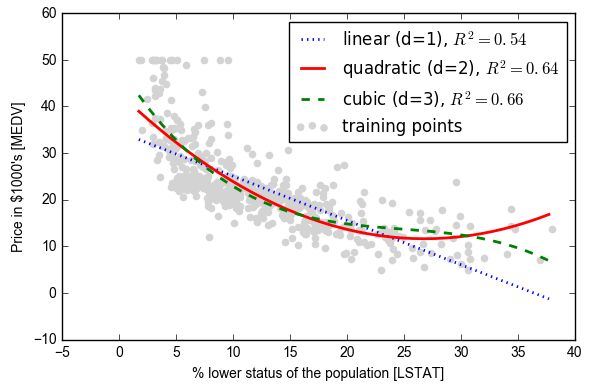
# plot results
plt.scatter(X, y, label='training points', color='lightgray')
plt.plot(X_fit, y_lin_fit, label='linear (d=1), $R^2=%.2f$' % linear_r2, color='blue', lw=2, linestyle=':')
plt.plot(X_fit, y_quad_fit, label='quadratic (d=2), $R^2=%.2f$' % quadratic_r2, color='red', lw=2, linestyle='-')
plt.plot(X_fit, y_cubic_fit, label='cubic (d=3), $R^2=%.2f$' % cubic_r2, color='green', lw=2, linestyle='--')
plt.xlabel('% lower status of the population [LSTAT]')
plt.ylabel('Price in $1000\'s [MEDV]')
plt.legend(loc='upper right')
plt.tight_layout()
# plt.savefig('./figures/polyhouse_example.png', dpi=300)
plt.show()

import numpy
from sklearn.tree import DecisionTreeRegressor
#http://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeRegressor.html#sklearn.tree.DecisionTreeRegressor
X = df[['LSTAT']].values
y = df['MEDV'].values
 
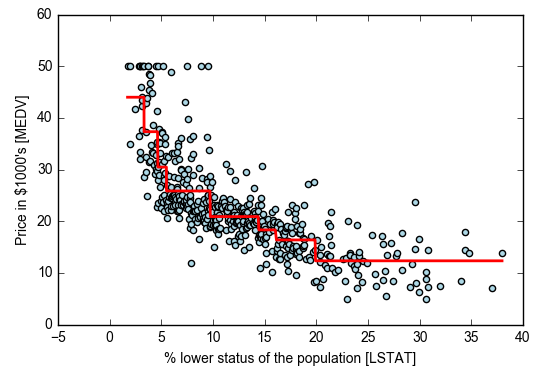
tree = DecisionTreeRegressor(max_depth=3)   #max_depth设置树深
tree.fit(X, y)   #参考官网attributes部分了解建模后得到的各种属性:树，使用的特征及特征重要性
 
sort_idx = X.flatten().argsort()   #X中最小元素到最大元素的索引构成的向量
 
lin_regplot(X[sort_idx], y[sort_idx], tree)
plt.xlabel('% lower status of the population [LSTAT]')
plt.ylabel('Price in $1000\'s [MEDV]')
# plt.savefig('./figures/tree_regression.png', dpi=300)
plt.show()
#水平红线表示c值，竖直红线表示特征列选择的切分点

随机森林回归

X = df.iloc[:, :-1].values   #13个特征列
y = df['MEDV'].values
 
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1)
from sklearn.ensemble import RandomForestRegressor
forest = RandomForestRegressor(n_estimators=1000, criterion='mse', random_state=1, n_jobs=-1)
forest.fit(X_train, y_train)
y_train_pred = forest.predict(X_train)
y_test_pred = forest.predict(X_test)
 
print('MSE train: %.3f, test: %.3f' % (mean_squared_error(y_train, y_train_pred),mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (r2_score(y_train, y_train_pred),r2_score(y_test, y_test_pred)))
#Output:
#MSE train: 1.642, test: 11.052
#R^2 train: 0.979, test: 0.878
plt.scatter(y_train_pred, y_train_pred - y_train, c='black', marker='o', s=35, alpha=0.5, label='Training data')
plt.scatter(y_test_pred, y_test_pred - y_test, c='lightgreen', marker='s', s=35, alpha=0.7, label='Test data')
plt.xlabel('Predicted values')
plt.ylabel('Residuals')
plt.legend(loc='upper left')
plt.hlines(y=0, xmin=-10, xmax=50, lw=2, color='red')
plt.xlim([-10, 50])
plt.tight_layout()
# plt.savefig('./figures/slr_residuals.png', dpi=300)
plt.show()

关注公众号：瑞行AI，欢迎交流AI算法、数据分析、leetcode刷题等技术，提供技术方案咨询和就业指导服务！