论文《Efficient Large-Scale Stereo Matching》学习

摘要

我们的方法通过对一组可进行鲁棒匹配的支撑点进行三角剖分，减少了剩余支撑点的匹配模糊性，从而在差异的基础上建立了先验。这允许有效地利用不均匀搜索空间，产生精确的密集重建而不需要全局优化。

1. 介绍

双目图像的深度估计是低层视觉的核心问题，是多视点重建等领域的重要组成部分。为了在自动驾驶等应用中具有实际应用价值，视差估计方法的运行速度应该类似于其他低级的视觉处理技术，例如边缘提取或兴趣点检测。由于深度误差随距离[1]呈二次增长，因此需要高分辨率图像来获得准确的三维表示。虽然高分辨率图像的优点在结构运动、目标识别和场景分类等方面已经得到了充分的利用，但只有少数双目立体方法能够有效地处理大图像。

基于局部对应的立体算法[2,3]通常速度较快，但需要适当选择窗口大小。如图1所示，这导致了小窗口大小的低匹配比和大窗口大小的边界出血伪影之间的权衡。因此，低纹理和模糊的表面不能一致匹配。

基于全局对应的算法[4-9]通过对正则化能量函数形式的差异施加平滑约束，克服了上述问题。由于这种基于mrf的能量函数的优化一般都是NP-hard，因此提出了多种近似算法，如图切割[4,5]或信念传播[6]。然而，即使是在低分辨率图像上，通常也需要大量的计算工作和高内存容量。例如，存储100万像素图像对的所有消息需要超过3gb的RAM[10]。在这些方法中，通常需要提前知道视差范围，正确选择正则化参数至关重要。此外，当提高图像分辨率时，广泛使用的基于二元势的先验不能重建纹理较差和倾斜的表面，因为它们倾向于正面平行的平面。最近开发的基于高阶团簇[7]的冰毒ods克服了这些问题，但对计算的要求更高。

本文提出了一种基于生成概率的立体匹配模型ELAS (Efficient scale stereo) ，该模型通过减少匹配的模糊性，实现了与小聚合窗口的密集匹配。我们的方法通过在一组称为“支持点”的鲁棒匹配对应项上形成三角剖分，在视差空间上建立先验。由于我们的先验是分段线性的，所以我们不会在纹理较差和倾斜的表面出现问题。这导致一个有效的算法，减少搜索空间，可以很容易地并行化。正如我们的实验所证明的，我们的方法能够实现最先进的性能，与流行的方法相比，速度显著提高了三个数量级;我们在一个CPU核心上获得300 MDE/s(每秒百万次视差评估)。

深度误差随距离呈二次增长

本文提出了一种用于立体匹配的生成概率模型ELAS,通过减少对应项上的歧义，允许与小聚合窗口进行密集匹配。我们的方法通过在一组称为“支持点”的鲁棒匹配对应项上形成三角剖分，在视差空间上建立先验。

2. Efficient Large-Scale Stereo Matching

我们的做法如下:
首先，利用全视差范围计算稀疏支持点集的视差。
然后，使用支持点的图像坐标通过Delaunay三角剖分创建一个二维网格。
通过计算先验值来消除匹配问题的歧义，将搜索限制在可信区域，从而提高了搜索效率。

2.1 support points

作为支持点，我们表示像素，因为它们的纹理和唯一性，可以进行很强的匹配。我们发现，利用9×9像素窗口的水平和垂直Sobel滤波器响应串联形成的向量之间的L1距离来匹配规则网格上的支持点是有效。

For robustness we impose consistency，只有当从左到右和从右到左匹配时，才保留通信。为了消除模糊匹配,我们排除了最佳匹配和次佳匹配之间的比例超过固定阈值的所有点,$\tau$= 0.9。通过删除所有显示与周围支持点不相似的视差值的所有点，可以消除虚假的不匹配。为了覆盖整个图像，我们在图像角上添加了额外的支持点，这些支持点的视差被认为是其最近邻居的视差。

2.2 Generative Model for Stereo Matching

我们现在描述我们的概率生成模型，给出一个参考图像和支持点，可以用来从另一个图像中提取样本。正式一点来讲：

令 S = { s 1 , . . . , s M } S = \left\{s_1 ,...,s_M \right\} S={s1​,...,sM​}为一组鲁棒匹配的支持点。每个支持点$s_m={\left(u_m,v_m,d_m\right)}^T$定义为其图像坐标$(u_m,v_m)\in {\mathbb{N}}^2$及其视差$d_m\in {\mathbb{N}}^2$的串联。设 O = { o 1 , . . . , o N } O = \left\{o_1 ,...,o_N \right\} O={o1​,...,oN​}为一组图像观测值，每个观测值$o_n=(u_n,v_n,fn{)}^T$构成其图像坐标$(u_n,v_n)\in {\mathbb{N}}^2$和特征向量$f_n\in {\mathbb{R}}^Q$的串联，例如，从一个小邻域计算出像素的强度或低维描述符。我们分别将$o_n^{(l)}$和$o_n^{(r)}$表示为左右图像中的观察值。在不失一般性的前提下，我们将左边的图像作为参考图像。

假设观测值$\left\{o_n^{(l)},o_n^{(r)}\right\}$和支持点S在给定视差$d_n$的情况下是有条件独立的。联合分布用$p(d_n|S,o_n^{(l)})$先验和$p(o_n^{(r)}|o_n^{(l)},d_n)$图像似然分解。

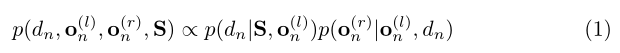
图2(a)描述了我们的方法的图形化模型。特别地，我们将先验值与均匀分布和采样高斯的组合成比例，用$\mu (S,o_n^{(l)})$表示连接支持点和观测值的平均函数，$N_S$是在一个20×20像素的小邻域$(u_n^{(l)},v_n^{(l)})$中所有支持点差异的集合。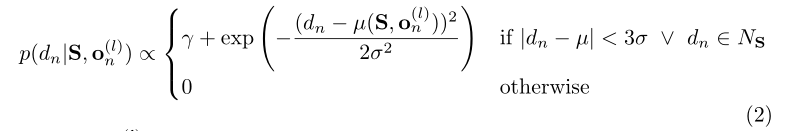
我们通过从平均值中排除所有大于3σ的视差值来提高效率。条件$d_n$∈$N_S$使得先验局部扩展其范围，更好地处理可能违反线性假设的视差不连续点。

我们将$\mu (S,o_n^{(l)})$表达为一个线性函数，它利用在支撑点上计算的Delaunay三角剖分法来插值这些视差。对于每个三角形，我们得到一个平面：

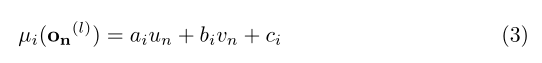
其中i是像素($u_n,v_n$)所在三角形的下标，$o_n=(u_n,v_n,fn{)}^T$是一个观察值。对于每个三角形，通过求解一个线性系统可以很容易地得到平面参数($a_i,b_i,c_i$)。因此，所提议的先验模式，μ，是支撑点视差之间的线性插值，用作粗略表示。

我们将图像的似然表示为一个受约束的拉普拉斯分布：

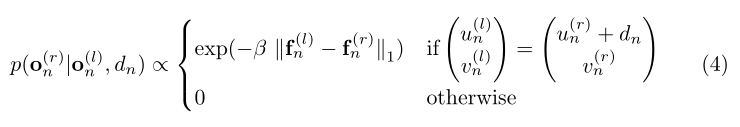
其中$f_n^{(l)},f_n^{(r)}$分别是左右图像的特征向量，并且$\beta$是常量值。如果条件确保对应位于同一极线上，并通过视差$d_n$进行匹配。在我们的实验中，将特征$f_n$作为一个5×5像素的邻域($u_n,v_n$)中图像导数的串联，根据Sobel滤波器响应计算，得到2×5×5=50维特征向量。根据经验，我们发现基于Sobel响应的特征比基于Laplacian-of-Gaussian (LoG)滤波器的特征工作得明显更好。

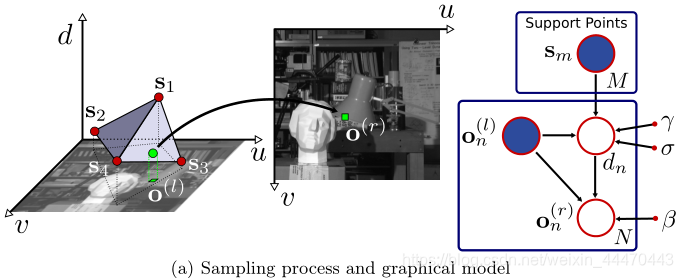
生成模型的一个优点是我们可以使用它来绘制样本，如图2(a)所示。给定左图中的支撑点和观测值，得到右图中相应观测值的样本如下:
1.给定S和$o_n^{(l)}$从$p(d_n|S,o_n^{(l)})$中得出视差$d_n$。
2.给定$o_n^{(l)}$和$d_n$从$p(o_n^{(r)}|o_n^{(l)},d_n)$得到观测值$o_n^{(r)}$

图2(b-d)描述了左侧输入图像，以及给定左侧图像和支持点，从右侧图像中提取的样本均值。为了在图2中得到一个全面的可视化，这里我们使用像素强度作为特征，每个像素绘制100个样本。如预期的那样，样本平均值对应于右侧图像的模糊版本。

2.3 Disparity Estimation(视差估计)

在前一节中，我们提出了一种用于立体匹配的先验和图像似然。我们还展示了如何绘制右图像的样本给定支持点和左图像中的观察值。然而，在推断时，我们感兴趣的是估计给定的左右图像的视差图。我们依靠最大后验(MAP)估计来计算视差：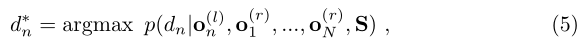
其中$o_1^{(r)}$，…，$o_N^{(r)}$表示右图中位于$o_n^{(l)}$极外线的所有观测值。后验可以分解为：

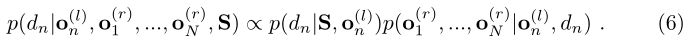
右图上沿极外线的观测是结构化的，即给定与$o_n^{(l)}$相关的视差，存在一个确定性映射，观测在该映射上具有非零概率。我们通过对沿极线所有观测值的分布进行建模来捕捉这一特性：

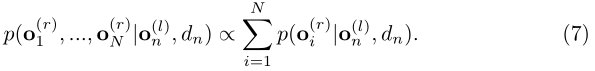
从式(4)中可知，对于每个$d_n$只有一个非零概率的观测值。将Eq.(2)和Eq.(4)代入Eq.(6)，取负对数得到一个能量函数，这个能量函数很容易最小化：

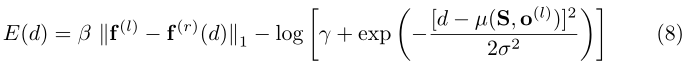
用$f^{(r)}(d)$表示特征向量位于像素($u^{(l)}-d,v^{(l)}$)处。注意，根据图像可能性的定义，仅当$|d-\mu |<3\sigma$，或d是相邻支撑点差异的一个元素时，才需要评估能量E(d)。重要的是，这可以对每个像素进行并行处理，因为支持点解耦了不同的观测值。
虽然在本节中我们着重于获取右侧图像的视差图，但是同样可以获得左侧视差图。在实践中，我们对两幅图像都应用了我们的方法，并执行左/右一致性检查，以消除遮挡区域中的虚假不匹配和差异。我们还删除了面积小于50像素的小片段。

3 Experimental Evaluation

在本节中，我们将比较我们的方法与最先进的方法在精度和运行时间方面的差异。在所有实验我们组$\beta$= 0.03,$\sigma$= 3,$\gamma$= 15和$\tau$= 0.9发现实证表现良好。我们使用库’ Triangle '[25]来计算三角形。所有的实验都是在一个运行在2.66 GHz的i7 CPU核心上进行的。由于我们的目标是在高分辨率图像上实现接近实时的速率，所以我们比较了在Middlebury数据集中处理大型图像的所有方法。这与文献中常用的450×375分辨率形成对比。