1.27马尔科夫链，抽样蒙特卡洛模拟（逆转化方法，接受拒绝矩阵），马尔科夫链蒙特卡洛MCMC，隐马尔科夫（HMM(V算法剪枝优化），NLP）_逆变换抽样、马尔可夫链蒙特卡罗(mcmc)方法和生成对抗网络(gans)

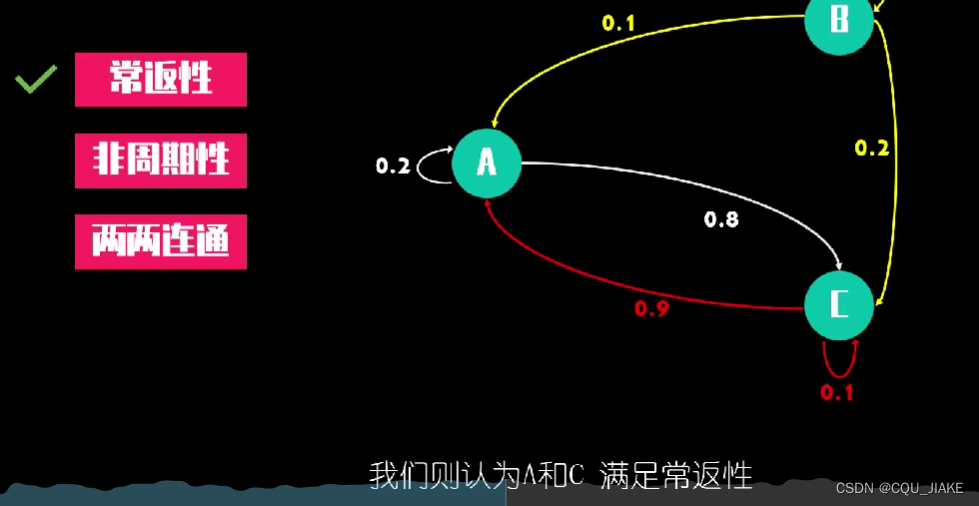
 马尔科夫链

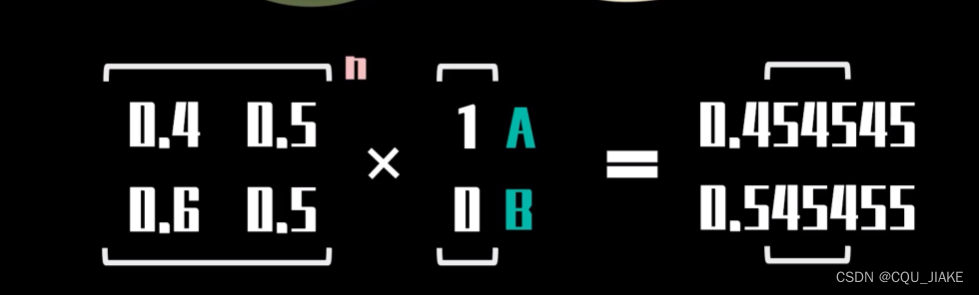
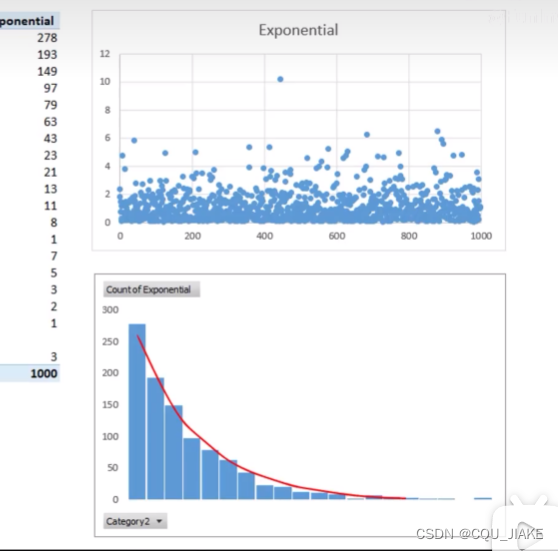
蒙特卡洛法模拟

抽样，逆转换方法

就是说由系统自带的随机函数RANDOM，通过下面这个方法，可以变为对应的随机模拟函数

 

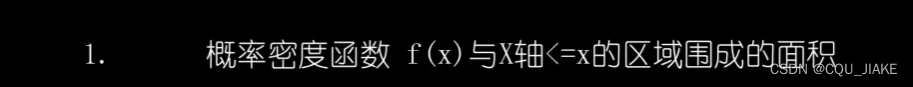
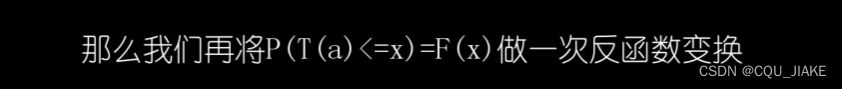
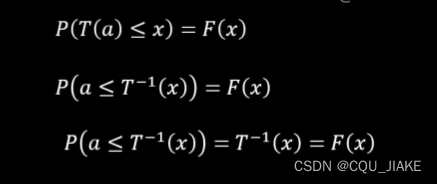
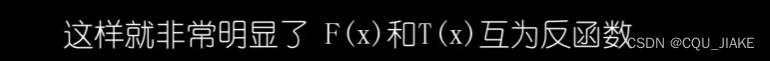
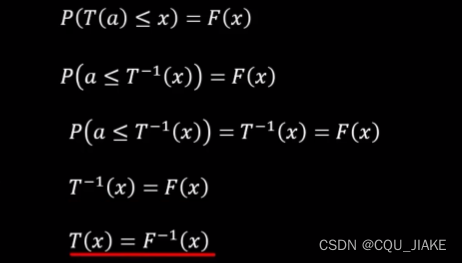
就是说要实现蒙特卡洛模拟，是要先有一个概率表达式，然后基于这个概率表达式，通过自带的随机RANDROM函数进行转换，最后实现这个表达式

而这个转换函数就是表达式的反函数

接受拒绝抽样

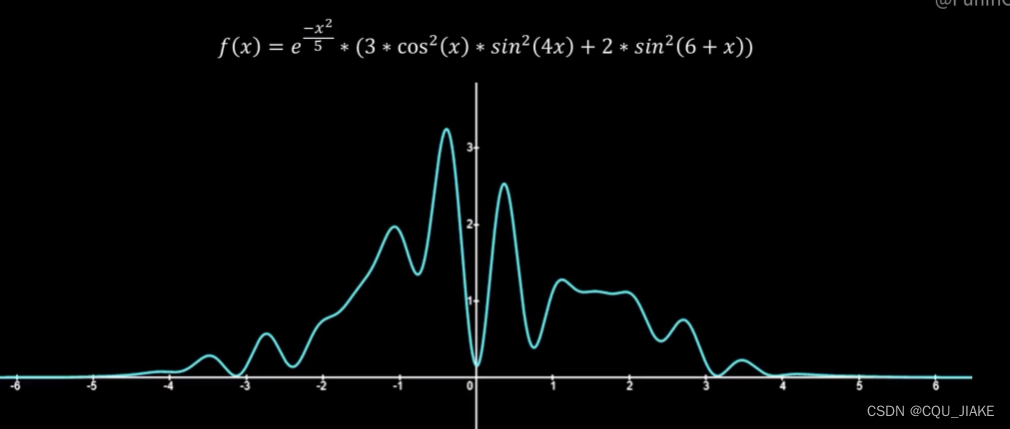
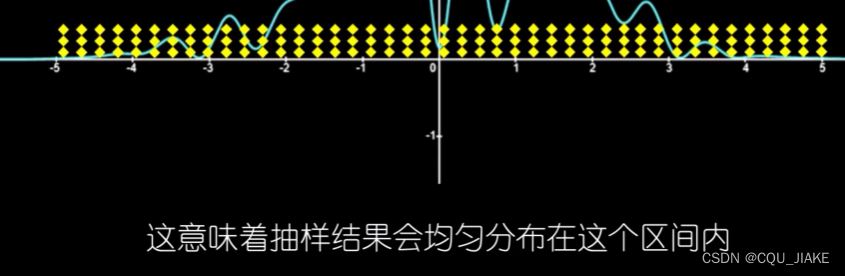
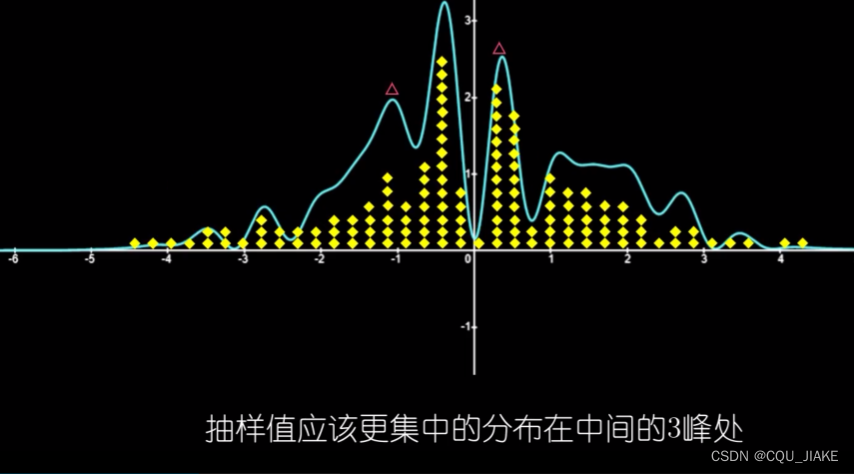
接受拒绝抽样

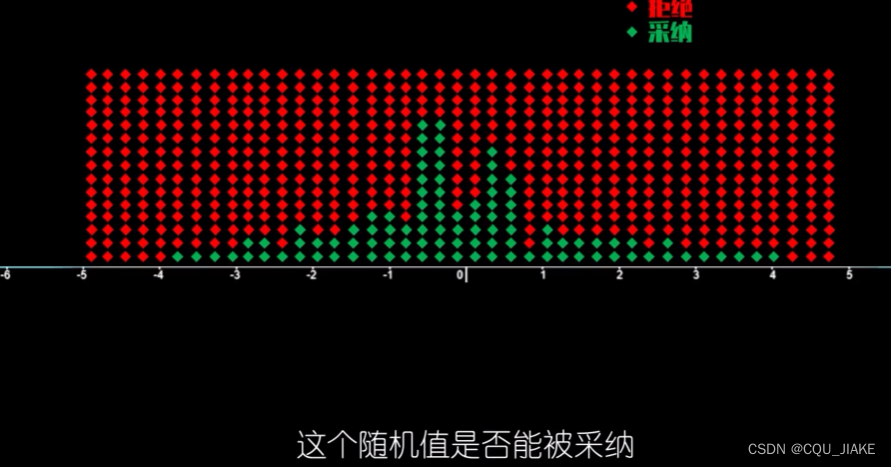
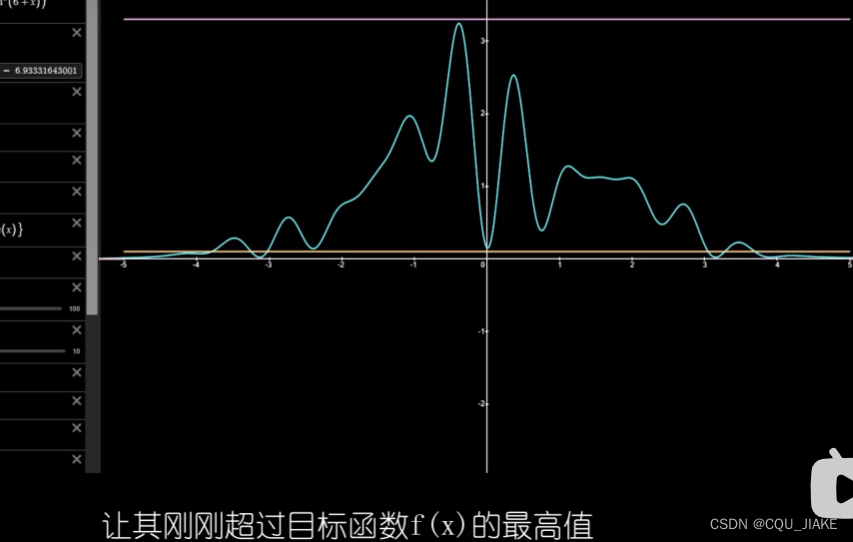
就是说要实现二维的随机模拟，就是要两个随机均匀分布函数，第一个是实现在-5到5的区间内，最大值为1的随机抽样，计为gx，它

就是先在定义域里随机取一个值a,然后计算目标函数在a下的值，接着由在0到最大值*ga上取一个值b，如果满足条件就接受a,不然就不接受；

就是第一次随机取样是水平的，取完后能确定一个横坐标，以及目标函数的纵坐标；第二次是在第一次取样的基础上再竖直上的取的，来判断第一次取的点能不能要

就是说第一次取样确定横坐标a，第二次取样确定纵坐标b，最后的取样点为(a,b)

1,如果a,b被采纳，就使横坐标a上对应的高度++，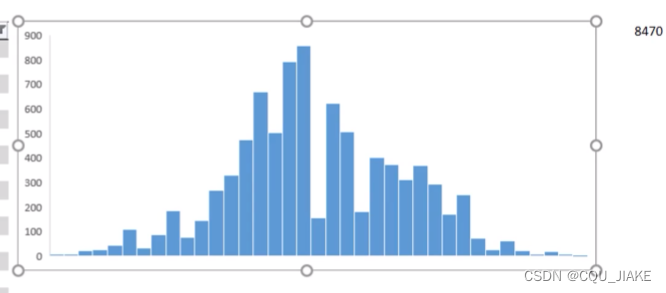

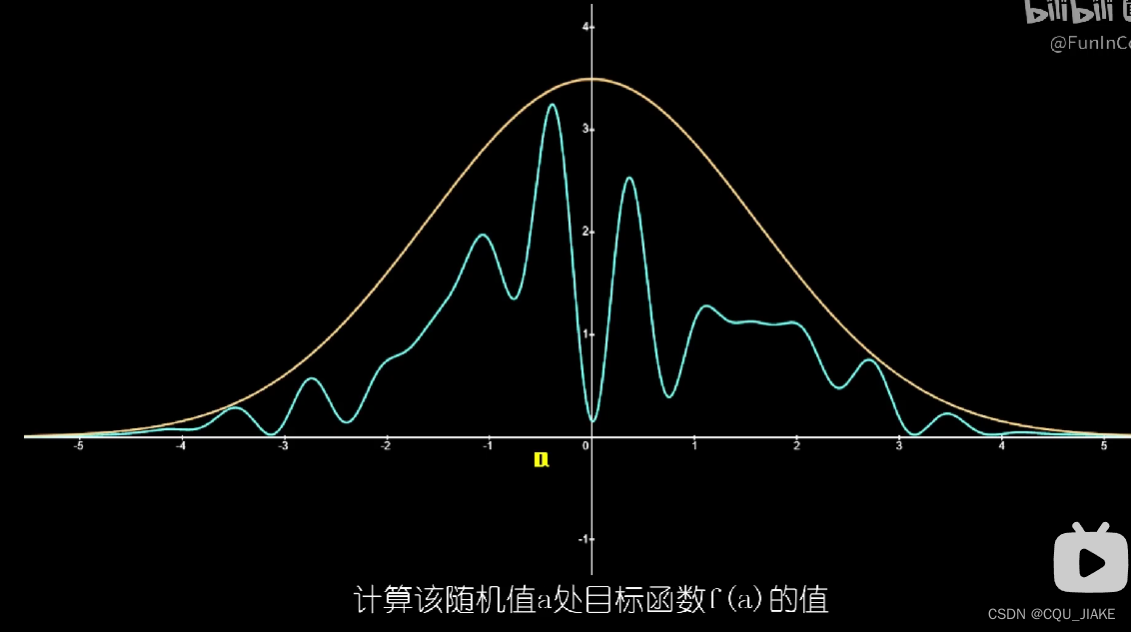
就是说第一步还是随机在定义域上选，然后在确定纵坐标时，上界不再是一个常数，而也是一个动态变化的天花板ZX,这样就能提高通过率

马尔科夫链蒙特卡洛法MCMC

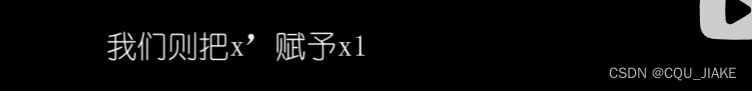
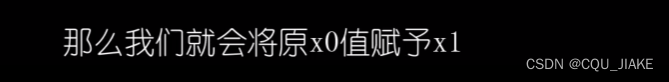
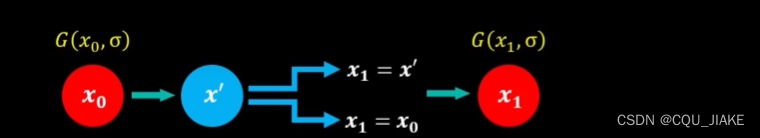
MH算法

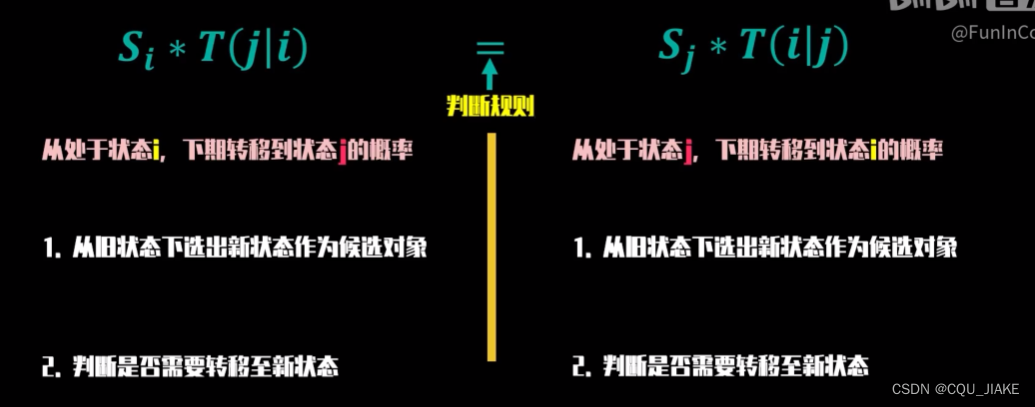
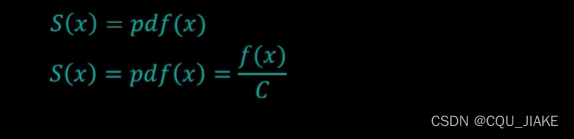
隐马尔可夫HMM

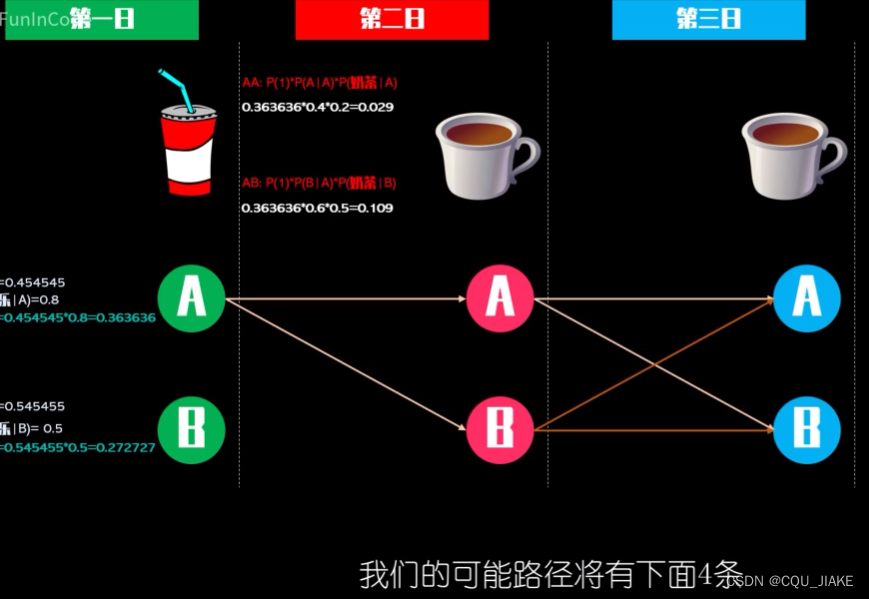
隐马尔可夫在NLP

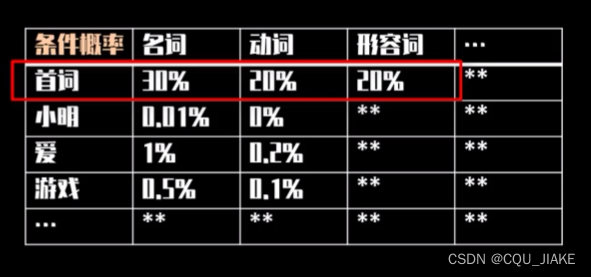
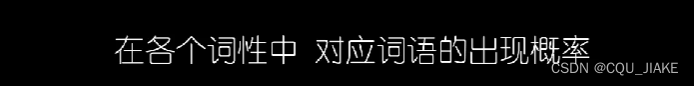
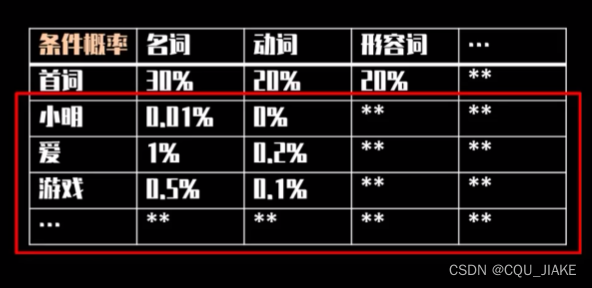
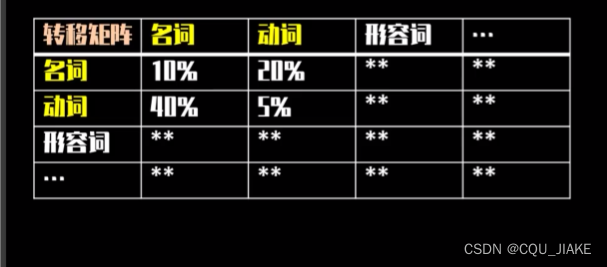
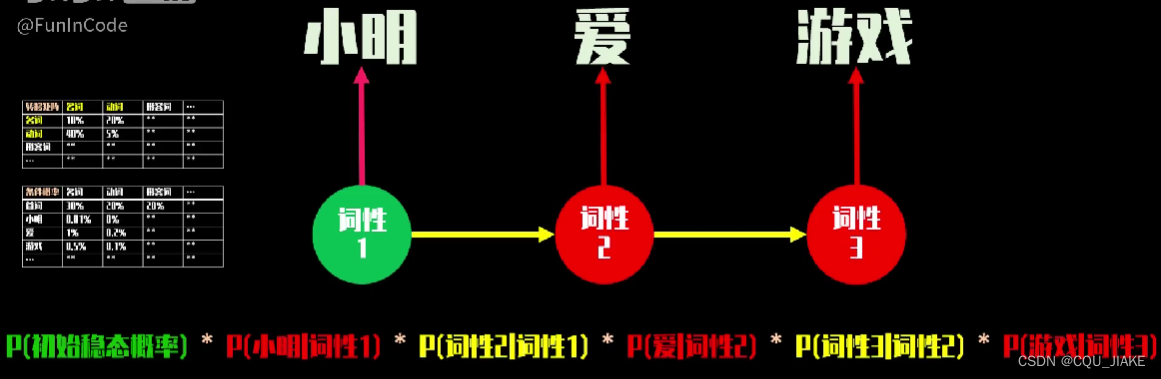
就是说，一个矩阵是描述整个句子结构构成的概率

另一个矩阵是在确定矩阵结构基础上，去选词，来确定这个句子的具体含义