- 1[精选]Kimi到底是什么,将带来什么?
- 2YOLOV7:OSError: [WinError 1455] 页面文件太小,无法完成操作的 最终解决方案_oserror: [winerror 1455] 页面文件太小,无法完成操作。 error load
- 3Git Bash 上传本地文件到Gitee(AI助力解决问题)_git bash gitee
- 4工赋开发者社区 | 「新一代知识图谱关键技术」最新2022进展综述_郭伟鹏 , 沈松雨 . 基于 bert 模型的领域知识图谱构建 研究 [j]. 科技创新与应用
- 5NLP全路径学习推荐
- 6屏幕距离识别加语音提醒
- 7深度学习-第T11周——优化器对比实验_优化器对比试验
- 8Stream流_using stream stream = new stream(stream)
- 9Anaconda 安装pytorch CUDA cudnn_anaconda pythorch cuda环境
- 10Transformer硬件实现第一篇:算法结构拆解_nv transformer硬件实现
SM2椭圆曲线公钥密码算法--密钥对与数字签名_sm2算法
赞
踩
1. SM2国密算法介绍
SM2算法全称是SM2椭圆曲线公钥密码算法(SM是商用密码的拼音缩写),是一种基于“椭圆曲线”的密码ECC(Elliptic Curve Cryptography)。2016年,SM2成为中国国家密码标准。 在商用密码体系中,SM2主要用于替换RSA加密算法。
SM2为非对称加密,基于ECC。该算法已公开。由于该算法基于ECC,故其签名速度与秘钥生成速度都快于RSA。ECC 256位(SM2采用的就是ECC 256位的一种)安全强度比RSA 2048位高,但运算速度快于RSA。旧标准的加密排序C1C2C3 新标准 C1C3C2,C1为65字节第1字节为压缩标识,这里固定为0x04,后面64字节为xy分量各32字节。C3为32字节。C2长度与原文一致。
国密SM2算法也是基于椭圆曲线公钥算法,椭圆曲线上的运算都是和国际算法一样的,国密SM2规范中给出了推荐曲线,所以首先需要加载国密推荐参数。
国密 SM2 的算法基础是椭圆曲线,公式:
算法是基于数学的,SM2 定义曲线上的群运算加减乘,通过SM2公私钥的生成理解。
-
首选一条椭圆曲线,即固定 a、b 的值,假设选择的是上图所示曲线。
-
随机选择一个点 P 为基点,曲线做切线,经过 Q 点,切点 R1。
-
基于 x 轴做 R1 的对称点 R,则 SM2 定义加法为 P + Q = R,这就是椭圆曲线加法。
-
求 2 倍点,当 P = Q 时,即 P + P = R = 2P,则 R 是 P 的 2 倍点。
-
求 3 倍点,3P = P + 2P = P + R,经过 P、R 做直线,交于椭圆曲线点 M1, 基于 x 轴对称点 M 则是 3 倍点,依次类推。
-
求 d 倍点,假设我们同样次数为 d,运算倍点为 Q。
-
d 为私钥,Q 为公钥。所以私钥是一个大整数,公钥是一个点坐标。
上面的几何推理是为了方便理解,实际取值都是在质数有限域上。密码专家们经过推理和运算,已经为我们选择了质数有限域上的最优椭圆曲线,除非有特殊需要,否则不需要自定义曲线。

2. 数据格式
ASN.1数据类型定义表
| Tag (decimal) | Tag (hex) | Type |
|---|---|---|
| 2 | 02 | INTEGER |
| 3 | 03 | BIT STRING |
| 4 | 04 | OCTET STRING |
| 5 | 05 | NULL |
| 6 | 06 | OBJECT IDENTIFIER |
| 12 | 0C | UTF8String |
| 16 | 10 (and 30)* | SEQUENCE and SEQUENCE OF |
| 17 | 11 (and 31)* | SET and SET OF |
| 19 | 13 | PrintableString |
| 22 | 16 | IA5String |
| 23 | 17 | UTCTime |
| 24 | 18 | GeneralizedTime |
2.1 密钥数据格式
2.1.1 私钥数据格式
SM2算法私钥数据格式的ASN.1定义为:
SM2PrivateKey ::= INTEGER
生成私钥:带“EC PARAMETERS”与不带“EC PARAMETERS”,只需要增加参数-noout。
- openssl ecparam -genkey -name SM2 -out sm2.key #带ec parameter
-
- -----BEGIN EC PARAMETERS-----
- BggqgRzPVQGCLQ==
- -----END EC PARAMETERS-----
- -----BEGIN EC PRIVATE KEY-----
- MHcCAQEEINlSELboVsYit7SgBFlM5Zny24X9a7TnyUaK5cTVydPMoAoGCCqBHM9V
- AYItoUQDQgAEw2I0OMqw39s0oin/S53J63C/GkFkWVR7H0b6063HqiInNVBEpfRF
- AWysN5eJydvHtwDJ6G6g5UbNp9lMjDXfCQ==
- -----END EC PRIVATE KEY-----
-
- openssl ecparam -genkey -name SM2 -out sm2.key -noout #不带ec parameter
-
- -----BEGIN EC PRIVATE KEY-----
- MHcCAQEEINlSELboVsYit7SgBFlM5Zny24X9a7TnyUaK5cTVydPMoAoGCCqBHM9V
- AYItoUQDQgAEw2I0OMqw39s0oin/S53J63C/GkFkWVR7H0b6063HqiInNVBEpfRF
- AWysN5eJydvHtwDJ6G6g5UbNp9lMjDXfCQ==
- -----END EC PRIVATE KEY-----

openssl ecparam默认生成SM2私钥格式是PEM,可以选择输出格式为DER。
openssl ec -in sm2.key -outform DER -out sm2_pri.der查看私钥密钥格式ASN.1内容
- openssl asn1parse -in sm2.key
-
- 0:d=0 hl=2 l= 119 cons: SEQUENCE
- 2:d=1 hl=2 l= 1 prim: INTEGER :01
- 5:d=1 hl=2 l= 32 prim: OCTET STRING [HEX DUMP]:D95210B6E856C622B7B4A004594CE599F2DB85FD6BB4E7C9468AE5C4D5C9D3CC
- 39:d=1 hl=2 l= 10 cons: cont [ 0 ]
- 41:d=2 hl=2 l= 8 prim: OBJECT :sm2
- 51:d=1 hl=2 l= 68 cons: cont [ 1 ]
- 53:d=2 hl=2 l= 66 prim: BIT STRING
-
- #ASN.1 Dump 私钥数据二进制文件
- dumpasn1 sm2_pri.der
-
- offset length
- 0 119: SEQUENCE {
- 2 1: INTEGER 1
- 5 32: OCTET STRING
- : D9 52 10 B6 E8 56 C6 22 B7 B4 A0 04 59 4C E5 99
- : F2 DB 85 FD 6B B4 E7 C9 46 8A E5 C4 D5 C9 D3 CC
- 39 10: [0] {
- 41 8: OBJECT IDENTIFIER sm2ECC (1 2 156 10197 1 301)
- : }
- 51 68: [1] {
- 53 66: BIT STRING
- : 04 C3 62 34 38 CA B0 DF DB 34 A2 29 FF 4B 9D C9
- : EB 70 BF 1A 41 64 59 54 7B 1F 46 FA D3 AD C7 AA
- : 22 27 35 50 44 A5 F4 45 01 6C AC 37 97 89 C9 DB
- : C7 B7 00 C9 E8 6E A0 E5 46 CD A7 D9 4C 8C 35 DF
- : 09
- : }
- : }
-
- 0 warnings, 0 errors.
-
- #hexdump 私钥二进制文件
- hexdump -v -e '/1 "%02x " ' -e '16/1 "" "\n"' sm2_pri.der
-
- 30 77 02 01 01 04 20 d9 52 10 b6 e8 56 c6 22 b7
- b4 a0 04 59 4c e5 99 f2 db 85 fd 6b b4 e7 c9 46
- 8a e5 c4 d5 c9 d3 cc a0 0a 06 08 2a 81 1c cf 55
- 01 82 2d a1 44 03 42 00 04 c3 62 34 38 ca b0 df
- db 34 a2 29 ff 4b 9d c9 eb 70 bf 1a 41 64 59 54
- 7b 1f 46 fa d3 ad c7 aa 22 27 35 50 44 a5 f4 45
- 01 6c ac 37 97 89 c9 db c7 b7 00 c9 e8 6e a0 e5
- 46 cd a7 d9 4c 8c 35 df 09

2.1.2公钥数据格式
公钥有两大种表示,通常是压缩或未压缩
2.1.2.1 未压缩公钥
通常以前缀04开头,后跟两个256位数字;一个用于点的x坐标,另一个用于点的y坐标。前缀04用于区分未压缩的公共密钥和以02或03开头的压缩公共密钥
即04||x||y
2.1.2.2 压缩公钥
因为方程式的左侧是,所以y的解是平方根,它可以具有正值或负值。所得的y坐标可以在x轴之上或之下。因为该曲线是对称的,所以它在x轴上像镜子一样反射。因此,我们必须存储y的符号(正数或负数);因为每个选项代表一个不同的点和一个不同的公钥。在素数为p的有限域上用二进制算术计算椭圆曲线时,y坐标为偶数或奇数,对应于前面所述的正/负号。所以为了区分y的两个可能值,如果y为偶数,则存储压缩的公钥,前缀为02,如果奇数为03,则允许软件从x坐标正确推断出y坐标,然后解压缩指向该点的完整坐标的公钥。
SM2算法公钥数据格式的ASN.1定义为:
SM2PublicKey ::= BIT STRING
SM2PublicKey为BIT STRING类型,内容为04‖X‖Y,其中,X和Y分别标识公钥的x分量和y分量,其长度各为256位。
生成公钥:
- openssl ec -in sm2.key -pubout -outform PEM -out sm2_pub.key
-
- -----BEGIN PUBLIC KEY-----
- MFkwEwYHKoZIzj0CAQYIKoEcz1UBgi0DQgAEw2I0OMqw39s0oin/S53J63C/GkFk
- WVR7H0b6063HqiInNVBEpfRFAWysN5eJydvHtwDJ6G6g5UbNp9lMjDXfCQ==
- -----END PUBLIC KEY-----
选择输出格式为DER
openssl ec -in sm2.key -pubout -outform DER -out sm2_pub.der查看私钥密钥格式ASN.1内容
- openssl asn1parse -in sm2_pub.key
-
- 0:d=0 hl=2 l= 89 cons: SEQUENCE
- 2:d=1 hl=2 l= 19 cons: SEQUENCE
- 4:d=2 hl=2 l= 7 prim: OBJECT :id-ecPublicKey
- 13:d=2 hl=2 l= 8 prim: OBJECT :sm2
- 23:d=1 hl=2 l= 66 prim: BIT STRING
-
- #ASN.1 Dump 公钥数据二进制文件
- dumpasn1 sm2_pub.der
-
- offset length
- 0 89: SEQUENCE {
- 2 19: SEQUENCE {
- 4 7: OBJECT IDENTIFIER ecPublicKey (1 2 840 10045 2 1)
- 13 8: OBJECT IDENTIFIER sm2ECC (1 2 156 10197 1 301)
- : }
- 23 66: BIT STRING
- : 04 C3 62 34 38 CA B0 DF DB 34 A2 29 FF 4B 9D C9
- : EB 70 BF 1A 41 64 59 54 7B 1F 46 FA D3 AD C7 AA
- : 22 27 35 50 44 A5 F4 45 01 6C AC 37 97 89 C9 DB
- : C7 B7 00 C9 E8 6E A0 E5 46 CD A7 D9 4C 8C 35 DF
- : 09
- : }
-
- 0 warnings, 0 errors.
-
- #hexdump 公钥二进制文件
- hexdump -v -e '/1 "%02x " ' -e '16/1 "" "\n"' sm2_pub.der
-
- 30 59 30 13 06 07 2a 86 48 ce 3d 02 01 06 08 2a
- 81 1c cf 55 01 82 2d 03 42 00 04 c3 62 34 38 ca
- b0 df db 34 a2 29 ff 4b 9d c9 eb 70 bf 1a 41 64
- 59 54 7b 1f 46 fa d3 ad c7 aa 22 27 35 50 44 a5
- f4 45 01 6c ac 37 97 89 c9 db c7 b7 00 c9 e8 6e
- a0 e5 46 cd a7 d9 4c 8c 35 df 09

2.2 加密数据格式
SM2算法加密后的数据格式的ASN.1定义为:
| SM2Cipher ::= SEQENCE { | ||
|---|---|---|
| XCoordinate | INTEGER, | -- x分量 |
| YCoordinate | INTEGER, | -- y分量 |
| HASH | OCTET STRING SIZE(32), | -- 杂凑值 |
| CipherText | OCTET STRING | -- 密文 |
| } |
其中,HASH为使用SM3算法对明文数据运算得到的杂凑值,其长度固定为256位。CipherText是与明文等长的密文。
参考sm2_demo.c加解密样例代码。
编译sm2_demo.c
gcc sm2_demo.c -L /usr/lib -lssl -lcrypto -o sm2_demo运行./sm2_demo 生成sm2_encrypt.bin文件。
- ./sm2_demo
- SM2 private key (in hex form):
- D95210B6E856C622B7B4A004594CE599F2DB85FD6BB4E7C9468AE5C4D5C9D3CC
-
- x coordinate in SM2 public key (in hex form):
- C3623438CAB0DFDB34A229FF4B9DC9EB70BF1A416459547B1F46FAD3ADC7AA22
-
- y coordinate in SM2 public key (in hex form):
- 27355044A5F445016CAC379789C9DBC7B700C9E86EA0E546CDA7D94C8C35DF09
-
- Message length: 16 bytes.
- Message:
- 0x00 0x01 0x02 0x03 0x04 0x05 0x06 0x07 0x08 0x09 0x0a 0x0b 0x0c 0x0d 0x0e 0x0f
-
- Ciphertext length: 123 bytes.
- Ciphertext (ASN.1 encode):
- 0x30
- 0x79 0x02 0x20 0x15 0xd6 0x7f 0xc3 0x84 0x21 0x7a 0x28 0xd5 0x89 0xaf 0x3a 0x09
- 0x32 0xf8 0xdf 0x03 0xd9 0xaa 0x3e 0x13 0x0b 0x46 0x17 0xe6 0x8d 0x0d 0x10 0xce
- 0xe9 0xe7 0x08 0x02 0x21 0x00 0xc5 0x60 0x37 0xbe 0x2a 0x33 0x84 0xb5 0x06 0xdd
- 0x48 0x6b 0x2c 0x3e 0xd2 0x2b 0xc1 0x81 0x6e 0x76 0x6b 0x7d 0x9d 0x69 0xcc 0x81
- 0x57 0x31 0x52 0xd5 0x1f 0xb1 0x04 0x20 0x26 0xfd 0xa6 0x66 0xf5 0x87 0x77 0x67
- 0x99 0x93 0x2a 0x5f 0x14 0x33 0x21 0x17 0xe9 0x0d 0x9d 0x1d 0xf3 0x81 0x8b 0x65
- 0x70 0xc3 0x79 0xa9 0xb7 0xd1 0xc7 0x96 0x04 0x10 0x3b 0x63 0x89 0x5a 0x35 0x7c
- 0x3d 0x4d 0x1f 0xad 0x73 0x0a 0xa1 0x89 0xc2 0x5f
-
- Decrypted plaintext length: 16 bytes.
- Decrypted plaintext:
- 0x00
- 0x01 0x02 0x03 0x04 0x05 0x06 0x07 0x08 0x09 0x0a 0x0b 0x0c 0x0d 0x0e 0x0f
-
- Encrypt and decrypt data succeeded!

查看加密数据格式ASN.1内容
- #ASN.1 Dump 加密数据二进制文件
- dumpasn1 sm2_encrypt.bin
-
- offset length
- 0 121: SEQUENCE {
- 2 32: INTEGER
- : 15 D6 7F C3 84 21 7A 28 D5 89 AF 3A 09 32 F8 DF
- : 03 D9 AA 3E 13 0B 46 17 E6 8D 0D 10 CE E9 E7 08
- 36 33: INTEGER
- : 00 C5 60 37 BE 2A 33 84 B5 06 DD 48 6B 2C 3E D2
- : 2B C1 81 6E 76 6B 7D 9D 69 CC 81 57 31 52 D5 1F
- : B1
- 71 32: OCTET STRING
- : 26 FD A6 66 F5 87 77 67 99 93 2A 5F 14 33 21 17
- : E9 0D 9D 1D F3 81 8B 65 70 C3 79 A9 B7 D1 C7 96
- 105 16: OCTET STRING 3B 63 89 5A 35 7C 3D 4D 1F AD 73 0A A1 89 C2 5F
- : }
-
- 0 warnings, 0 errors.
-
- #hexdump 数字签名二进制文件
- hexdump -v -e '/1 "%02x " ' -e '16/1 "" "\n"' sm2_encrypt.bin
-
- 30 79 02 20 15 d6 7f c3 84 21 7a 28 d5 89 af 3a
- 09 32 f8 df 03 d9 aa 3e 13 0b 46 17 e6 8d 0d 10
- ce e9 e7 08 02 21 00 c5 60 37 be 2a 33 84 b5 06
- dd 48 6b 2c 3e d2 2b c1 81 6e 76 6b 7d 9d 69 cc
- 81 57 31 52 d5 1f b1 04 20 26 fd a6 66 f5 87 77
- 67 99 93 2a 5f 14 33 21 17 e9 0d 9d 1d f3 81 8b
- 65 70 c3 79 a9 b7 d1 c7 96 04 10 3b 63 89 5a 35
- 7c 3d 4d 1f ad 73 0a a1 89 c2 5f

2.3 签名数据格式
SM2 签名一般有两种数据格式,国标(GM/T 0009-2012 SM2 密码算法使用规范)规定签名数据格式,使用ASN.1 格式定义,具体格式如下: 通常使用硬件加密机加签产生的数字数字签名将会使用这种格式。SM2 数字签名另外一种方式就比较简单,格式为R|S,即直接将两者拼接在一起表示。
SM2算法签名数据格式的ASN.1定义为:
| SM2Signature ::= SEQUENCE{ | ||
|---|---|---|
| R | INTEGER, | -- 签名值的第一部分 |
| S | INTEGER | -- 签名值的第二部分 |
| } |
R和S的长度各为256位。
对SM2公钥SM3杂凑值进行数字签名:
- openssl sm3 sm2_pub.der
- SM3(sm2_pub.der)= a760be75c573ac4c0a2350da375b52265ebb2623774c58a446c1b8751c8fbcf8
-
- #生成SM2公钥SM3杂凑值二进制文件
- openssl dgst -sm3 -binary sm2_pub.der > sm3_pub.bin
-
- hexdump -v -e '/1 "%02x " ' -e '16/1 "" "\n"' sm3_pub.bin
-
- a7 60 be 75 c5 73 ac 4c 0a 23 50 da 37 5b 52 26
- 5e bb 26 23 77 4c 58 a4 46 c1 b8 75 1c 8f bc f8
-
- #生成数字签名二进制文件
- openssl dgst -sign sm2.key -out sm2_pk_sm3.sign sm3_pub.bin
-
- #ASN.1 Dump 数字签名二进制文件
- dumpasn1 sm2_pk_sm3.sign
-
- offset length
- 0 68: SEQUENCE {
- 2 32: INTEGER
- : 21 80 5A 21 15 C7 68 31 06 80 6D 7B E7 44 F3 BD
- : 1A EF 23 04 97 81 6D 3C 2C FD 90 83 BE AC 9F 0B
- 36 32: INTEGER
- : 1A DC 37 70 B6 5D 31 7B 2C 65 8B 81 96 6A 2E F8
- : C6 A5 FD A7 BA DA 7F 0D 69 42 6E D3 A7 1C CA E2
- : }
- 0 warnings, 0 errors.
-
- #hexdump 数字签名二进制文件
- hexdump -v -e '/1 "%02x " ' -e '16/1 "" "\n"' sm2_pk_sm3.sign
-
- 30 44 02 20 21 80 5a 21 15 c7 68 31 06 80 6d 7b
- e7 44 f3 bd 1a ef 23 04 97 81 6d 3c 2c fd 90 83
- be ac 9f 0b 02 20 1a dc 37 70 b6 5d 31 7b 2c 65
- 8b 81 96 6a 2e f8 c6 a5 fd a7 ba da 7f 0d 69 42
- 6e d3 a7 1c ca e2

3. SM2数字签名与验签算法流程
3.1 数字签名算法符号定义:
A,B:使用公钥密码系统的两个用户。
dA:用户A的私钥。
E(Fq): Fq上椭圆曲线E 的所有有理点(包括无穷远点O)组成的集合。
e:密码杂凑函数作用于消息M的输出值。
e′:密码杂凑函数作用于消息M ′的输出值。
Fq:包含q个元素的有限域。
G:椭圆曲线的一个基点,其阶为素数。
Hv():消息摘要长度为v比特的密码杂凑函数。
IDA:用户A的可辨别标识。
M:待签名的消息。
M′:待验证消息。
modn:模n运算。例如, 23mod7=2。
n:基点G的阶(n是#E(Fq)的素因子)。
O:椭圆曲线上的一个特殊点,称为无穷远点或零点,是椭圆曲线加法群的单位元。
PA:用户A的公钥。
q:有限域Fq中元素的数目。
a,b: Fq中的元素,它们定义Fq上的一条椭圆曲线E。
x ∥ y: x与y的拼接,其中x、 y可以是比特串或字节串。
ZA:关于用户A的可辨别标识、部分椭圆曲线系统参数和用户A公钥的杂凑值。
(r,s):发送的签名。
(r′,s′):收到的签名。
[k]P:椭圆曲线上点P的k倍点,即, [k]P= P + P + · · · + P(k个P, k是正整数)。
[x,y]:大于或等于x且小于或等于y的整数的集合。
数字签名算法由一个签名者对数据产生数字签名,并由一个验证者验证签名的可靠性。每个签名者有一个公钥和一个私钥,其中私钥用于产生签名,验证者用签名者的公钥验证签名。在签名的生成程之前,要用密码杂凑算法对 M(包含和待签消息 M)进行压缩;在验证过程之前,要用密码杂凑算法对 M'(包含
和待验证消息 M')进行压缩。作为签名者的用户 A 具有长度为entlenA比特的可辨别标识IDA,记ENTLA 是由整数entlenA 转换而成的两个字节,在本部分规定的椭圆曲线数字签名算法中,签名者和验证者都需要用密码杂凑算法求得用户 A 的杂凑值
。按 GB/T32918.1—2016中4.2.6和4.2.5给出的方法,将椭圆曲线方程参数a、b、G 的坐标
、
和
的坐标
、
,
的数据类型转换为比特串。
3.2 数字签名的生成算法及流程
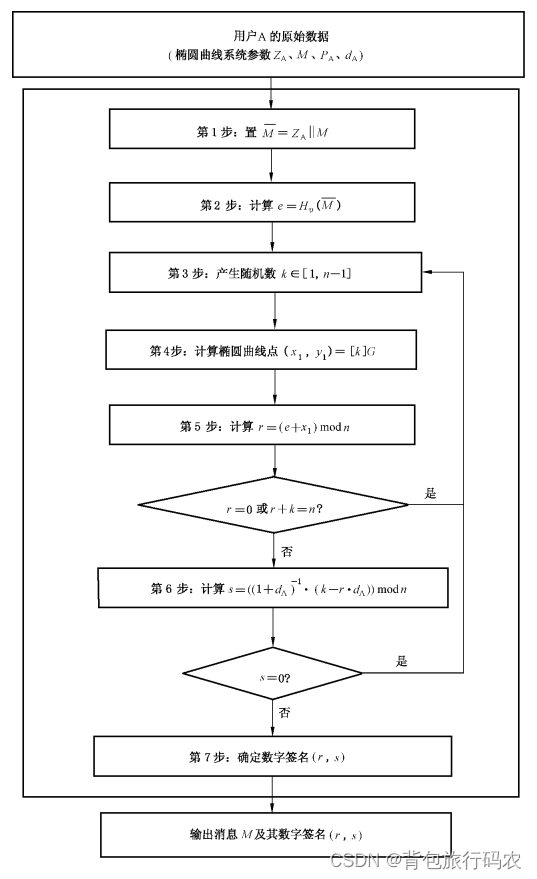
3.2.1 数字签名的生成算法
设待签名的消息为 M,为了获取消息 M 的数字签名(r,s),作为签名者的用户 A 应实现以下运算步骤:

3.2.2 数字签名生成算法流程
3.3 数字签名的验证算法及流程
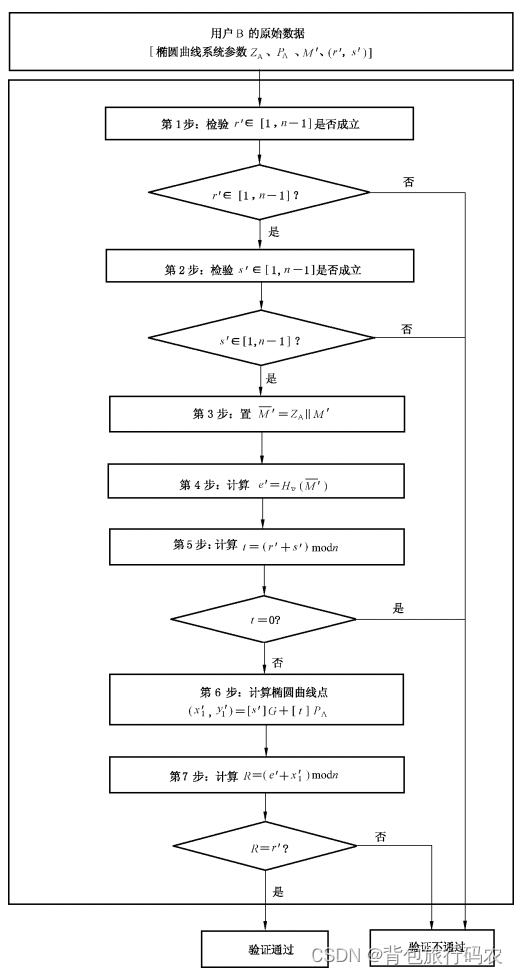
3.3.1 数字签名的验证算法
为了检验收到的消息 M' 及其数字签名(r',s'),作为验证者的用户 B应实现以下运算步骤:

3.3.2 数字签名验证算法流程
参考文献
SM2国密算法/椭圆曲线密码学ECC之数学原理 - 简书 (jianshu.com)
Elliptic Curve Cryptography: a gentle introduction - Andrea Corbellini


