- 1PS2游戏操纵杆_ps2摇杆模块的使用
- 2从零开始使用react+Ant Design撸一个后台管理系统(一)_ant design +react 后台管理项目
- 314 个实用的 SQL 拿来就用语句实例!_sql实例
- 4如何远程访问 RabbitMQ_rabbitmq开启远程访问
- 5【郭东白架构课 模块二:创造价值】17|通用技能(下):架构师如何保障交付与沉淀知识?_郭东白 架构
- 6vue+百度语音合成(TTS)实现语音播报功能_vue 监听百度tts语音播报
- 7喜报 | 英码科技顺利通过2023年度广东省工程技术研究中心认定
- 8C++11 call_once/once_flag 使用_std::once_flag 重置方法
- 9真的,kafka 入门看这一篇准没错!_partition is not a recognized option
- 10catboost模型建立
蚁群(ACO)算法简介
赞
踩
前言
生活中我们总能看到一群蚂蚁按照一条非常有规律的路线搬运食物回到巢穴,而且每只蚂蚁的路线都是近似相同且较优的,这种方法如果运用到我们的优化计算中效果会不会很好呢?
一、 ACO简介
1. 起源
蚁群系统(Ant System或Ant Colony System)是由意大利学者Dorigo、Maniezzo等人于20世纪90年代首先提出来的。他们在研究蚂蚁觅食的过程中,发现单个蚂蚁的行为比较简单,但是蚁群整体却可以体现一些智能的行为。
百度百科定义:蚁群算法是一种用来寻找优化路径的概率型算法。它由Marco Dorigo于1992年在他的博士论文中提出,其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。
2. 思想
将起点到食物源的路径视为待优化问题,蚂蚁行走的路径视为问题的可行解,整体蚂蚁群体的所有路径构成问题的解空间;
蚂蚁群体之所以能找最短路径,主要依赖于信息素这一机制,蚂蚁在行走过程中会释放信息素,每次往返时间最短的蚂蚁重复频率最快,在路径上所留下的信息素最多,久而久之,对应的路径上的信息素越来越多,其他蚂蚁根据信息素的浓度会优先选择浓度最高的路径,也就是最短路径。
3. 基本概念
3.1 并行
蚁群算法中每只蚂蚁的搜索相对独立,可以同时在多点开始进行独立的解搜索,有效地提高了全局搜索能力
3.2 禁忌表
禁忌表,用于存放第 k k k 只蚂蚁已经走过的城市
3.3 启发式信息
蚂蚁 k k k 从城市 i i i 转移到 j j j 的期望程度(即概率)
4. 流程
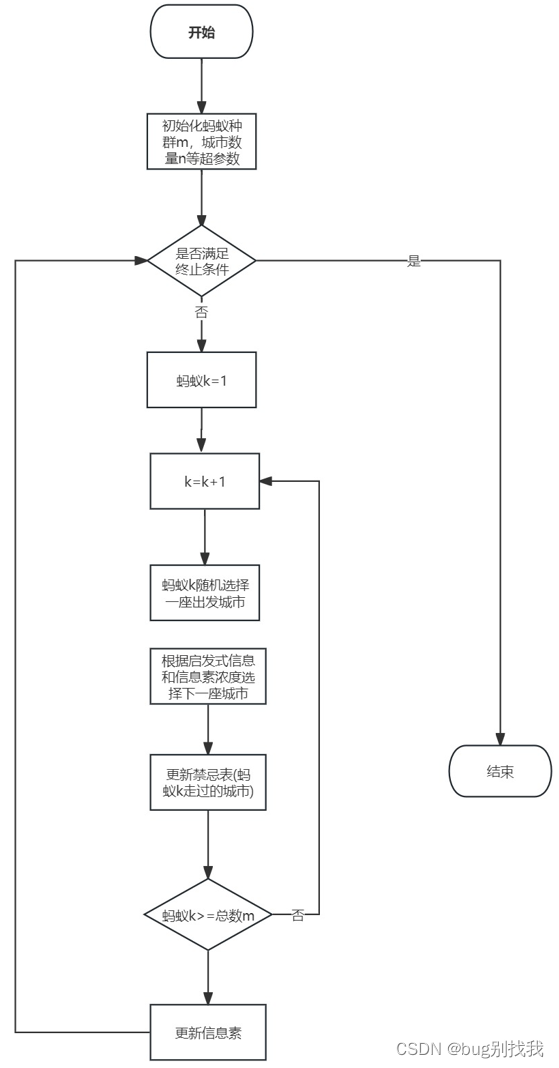
-
初始化蚂蚁群体数量 m m m,城市数量 n n n,信息素重要程度因子 α α α,启发式函数重要因子 β β β,信息素挥发因子 ρ ρ ρ
-
每只蚂蚁随机选择一座城市并行出发
-
根据信息素浓度和启发式信息选择下一座城市,下为蚂蚁 k k k 从城市 i i i 转移到城市 j j j 的概率公式
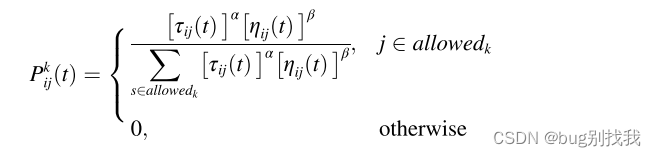
τ i , j ( t ) τ_{i,j}(t) τi,j(t)为时间为 t t t 时城市 i i i 到城市 j j j 的信息素浓度, α α α 为信息素重要程度因子(超参数);
η i , j ( t ) η_{i,j}(t) ηi,j(t)为时间为 t t t 时从第 i i i 座城市到第 j j j 座城市的启发信息, β β β为启发式函数重要因子(超参数);
η i , j ( t ) = 1 / d i , j η_{i,j}(t)=1/{d_{i,j}} ηi,j(t)=1/di,j, d i , j d_{i,j} di,j为第 i i i 座城市到第 j j j 座城市的欧几里得距离;
a l l o w e d k allowed_k allowedk为蚂蚁k在城市 i i i 的可选择后续城市集合。 -
每只蚂蚁从第 i i i 座城市走到第 j j j 座城市进行局部信息素更新
τ i , j ( t ) = ( 1 − ϑ ) τ i , j ( t ) + ϑ τ 0 τ_{i,j}(t) = (1− ϑ)τ_{i,j}(t)+ϑτ_0 τi,j(t)=(1−ϑ)τi,j(t)+ϑτ0
ϑ为局部信息素更新因子 -
当所有蚂蚁都完成了一次循环,进行全局信息素更新
τ i , j ( t + 1 ) = ( 1 − ρ ) τ i , j ( t ) + ρ Δ τ i , j ( t ) τ_{i,j}(t+1) = (1− ρ)τ_{i,j}(t)+ρΔτ_{i,j}(t) τi,j(t+1)=(1−ρ)τi,j(t)+ρΔτi,j(t)Δ τ i , j ( t ) = ∑ k = 1 m Δ τ i , j k ( t ) Δτ_{i,j}(t) =∑^m_{k =1}Δτ^k_{i,j}(t) Δτi,j(t)=∑k=1mΔτi,jk(t)
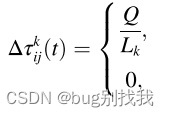
Q是信息素强度的初始值; L k L_k Lk是蚂蚁 k k k 的迭代路径的总长度, ρ ρ ρ为信息素挥发因子 。


