【算法】莫队算法

莫队算法概述：

莫队算法是由莫涛发明的算法，所以称为莫队算法。
莫队算法是一个对于区间、树或其他结构离线（在线）维护的算法，此算法基于一些基本算法，例如暴力维护，树状数组，分块，最小曼哈顿距离生成树，对其进行糅合从而产生的算法
其主要用来处理离线的区间问题，如区间和。看到这你会想到线段树，但是他与线段树相比，优点就是可以处理离散的信息，而且代码量小。

算法过程：

• 对于多段区间的询问,先将询问区间离线存储下来,然后再从左到右扫一遍,在过程中维护一段区间,就可以得到每个寻问区间的答案.
• 但是暴力扫肯定不行，所以在扫之前，要对所有询问区间进行一番操作——sort！使得能够在移动次数最少的情况下,得到所有询问的区间.
• sort之前要先分块：为每一个询问区间添加一个变量——块号。将数轴上的n个数字分为 $\sqrt{n}$ 块，每一块内有 $\sqrt{n}$ 个数字，每一个询问区间的块号就是该区间的左端点所在的块号。
• sort的规则：对于两个询问区间，若其块号相同（即 l 所在的块相同），那么将其 r 作为关键字从小到大排序；若其块号不同（即 l 所在的块不相同），就将 l 作为关键字从小到大排序。
• 这样排序后，维护全局的左右指针，使得它每次指向询问区间的左端点和右端点。从左到右扫一遍，处理每一个询问区间，计算答案了。

排序后的询问区间的移动如下图中蓝色区间向绿色区间的移动。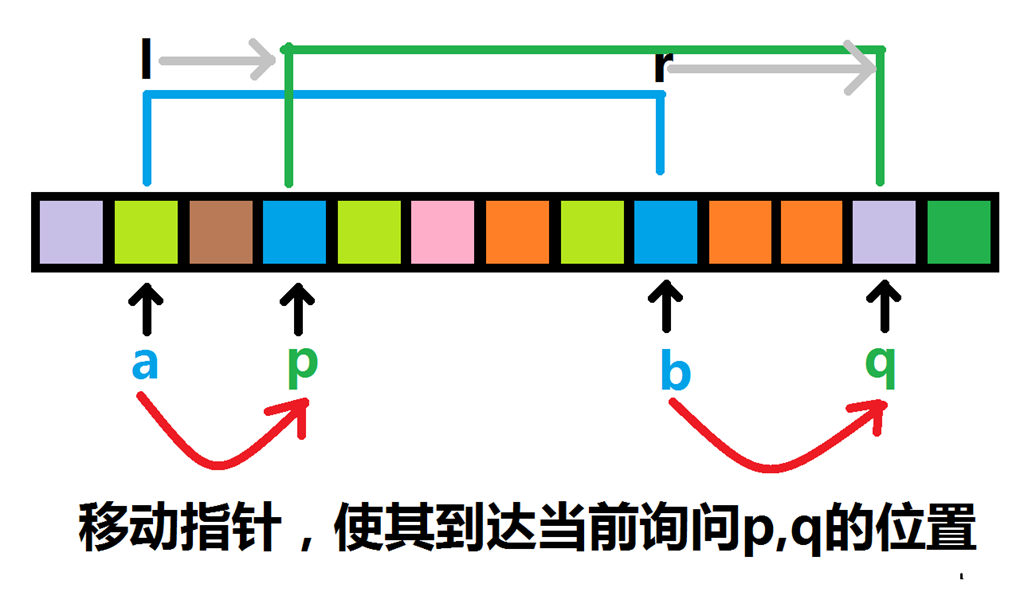

时间复杂度：

假设有n个点，m个询问区间，分块大小为 size = $\sqrt{n}$。

分类讨论：

① $l$ 的移动：若下一个询问与当前询问的 $l$ 所在的块不同，那么只需要经过最多$2\ast size$步可以使得$l$成功到达目标。复杂度为：$O(m\ast size)$

② $r$ 的移动：$r$ 只有在区间的块号相同时才会有序，其余时候还是疯狂地乱跳，那么每一次最坏就要跳$n$次！对于每一个块，排序执行第二关键字：$r$。所以这里面的r是单调递增的，所以枚举完一个块，$r$ 最多移动 $n$ 次。总共有 $n/size$ 个块:复杂度为：$O(n\ast n/size)$

总结：$O(n\ast size+n\ast n/size)$（n,m 同级，所以统一使用n）

当 $size=\sqrt{n}$ 时，莫队算法的真正复杂度：$O(n\ast \sqrt{n})$

例题：

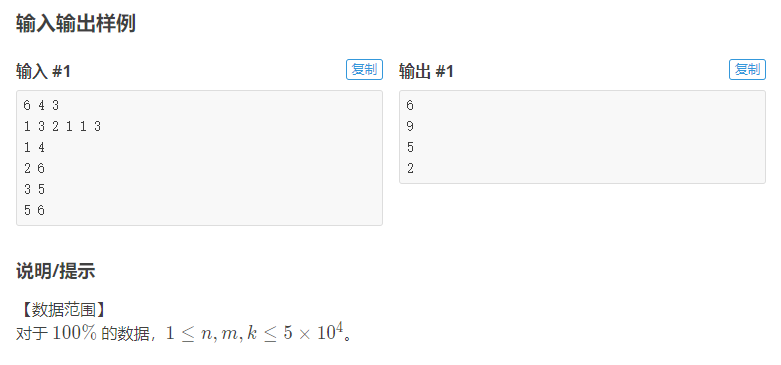
1.洛谷P2709 小B的询问

代码思路：

1.对于询问区间的离线化分块处理

struct Query{
	int l,r,id,block;//区间左端点 区间右端点 询问的序号 所属的块号
	bool operator < (const Query& q)const//重写<运算符适应sort的规则
	{
		if(block==q.block)
			return r<q.r;
		else
			return block<q.block;
	}
}q[MAXN];
1
2
3
4
5
6
7
8
9
10

2.求取每一个区间的答案（先展示暴力的思路）

//a[i]：第i位的数字 cnt[i]：数字i出现的次数
for(int i=l;i<=r;i++)
{
	tmp-=(cnt[a[i]]*cnt[a[i]]);
	cnt[a[i]]++;
	tmp+=(cnt[a[i]]*cnt[a[i]]);
}
1
2
3
4
5
6
7
8

3.指针移动（莫队核心）

for(int i=2;i<=m;i++)
	{
		while(l<q[i].l)//l右移 
		{
			tmp-=(cnt[a[l]]*cnt[a[l]]);
			cnt[a[l]]--;
			tmp+=(cnt[a[l]]*cnt[a[l]]);
			l++;
		}
		while(l>q[i].l)//l左移 
		{
			l--;
			tmp-=(cnt[a[l]]*cnt[a[l]]);
			cnt[a[l]]++;
			tmp+=(cnt[a[l]]*cnt[a[l]]);
		}
		while(r<q[i].r)//r右移 
		{
			r++;
			tmp-=(cnt[a[r]]*cnt[a[r]]);
			cnt[a[r]]++;
			tmp+=(cnt[a[r]]*cnt[a[r]]);
		}
		while(r>q[i].r)//r左移 
		{
			tmp-=(cnt[a[r]]*cnt[a[r]]);
			cnt[a[r]]--;
			tmp+=(cnt[a[r]]*cnt[a[r]]);
			r--;
		}
		ans[q[i].id]=tmp;
		l=q[i].l;
		r=q[i].r;
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

完整代码：

#include <bits/stdc++.h>
#include <iostream>
#include <string.h>
#define ll long long
#define qc ios::sync_with_stdio(false); cin.tie(0);cout.tie(0)
using namespace std;
const int MAXN = 5e4 + 7;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;

struct Query{
	int l,r,id,block;
	bool operator < (const Query& q)const
	{
		if(block==q.block)
			return r<q.r;
		else
			return block<q.block;
	}
}q[MAXN];

int a[MAXN],n,m,k;
ll cnt[MAXN],ans[MAXN];

int main()
{
//	freopen("in.txt", "r", stdin);
	qc;
	cin>>n>>m>>k;
	int size=sqrt(n);
	for(int i=1;i<=n;i++)
		cin>>a[i];
	int l,r;
	for(int i=1;i<=m;i++)
	{
		cin>>l>>r;
		q[i].l=l;
		q[i].r=r;
		q[i].id=i;
		q[i].block=(l-1)/size+1;// l/r上取整 
	}
	sort(q+1,q+m+1);
	l=r=1; 
	ll tmp=0;
	for(int i=q[1].l;i<=q[1].r;i++)//暴力计算第一个询问区间答案 
	{
		tmp-=(cnt[a[i]]*cnt[a[i]]);
		cnt[a[i]]++;
		tmp+=(cnt[a[i]]*cnt[a[i]]);
	}
	l=q[1].l;
	r=q[1].r;
	ans[q[1].id]=tmp;
	for(int i=2;i<=m;i++)
	{
		while(l<q[i].l)//l右移 
		{
			tmp-=(cnt[a[l]]*cnt[a[l]]);
			cnt[a[l]]--;
			tmp+=(cnt[a[l]]*cnt[a[l]]);
			l++;
		}
		while(l>q[i].l)//l左移 
		{
			l--;
			tmp-=(cnt[a[l]]*cnt[a[l]]);
			cnt[a[l]]++;
			tmp+=(cnt[a[l]]*cnt[a[l]]);
		}
		while(r<q[i].r)//r右移 
		{
			r++;
			tmp-=(cnt[a[r]]*cnt[a[r]]);
			cnt[a[r]]++;
			tmp+=(cnt[a[r]]*cnt[a[r]]);
		}
		while(r>q[i].r)//r左移 
		{
			tmp-=(cnt[a[r]]*cnt[a[r]]);
			cnt[a[r]]--;
			tmp+=(cnt[a[r]]*cnt[a[r]]);
			r--;
		}
		ans[q[i].id]=tmp;
		l=q[i].l;
		r=q[i].r;
	}
	for(int i=1;i<=m;i++)
		cout<<ans[i]<<endl;
	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92

2.HDU - 6959 zoto

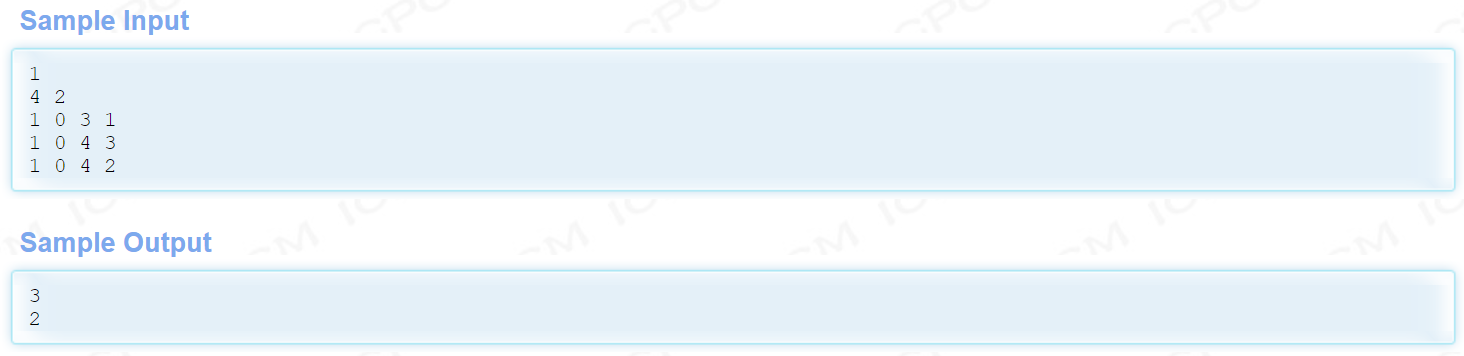
题目大意：

给你 $n$ 个数的序列 $x_i$，代表 $n$ 个点的纵坐标，横坐标是他们在序列中的位置，即 $(i,x_i)$ 构成 $n$ 个点。有 $m$ 次询问，每次给出一个矩形的左下方坐标 $x_0,y_0$ ，右上方坐标 $x_1,y_1$ ，求问在这个矩形内的点（包括边界）有多少纵坐标不同的点。

代码思路：

1.分块
将x轴分块，方便使用莫队算法计算区间答案

struct 	Query{
	int lx,ly,rx,ry,id,block;//左下角x坐标 左下角y坐标 右上角x坐标 右上角y坐标 询问的序号 所属块号
	bool operator < (const Query& q)const
	{
		if(block!=q.block)//块号不同，按照块号排序 
			return block<q.block;
		else//块号相同 ，按照右边界x坐标排序 
			return rx<q.rx;
	}
}q[MAXN];
1
2
3
4
5
6
7
8
9
10

将y轴分块，方便计算该块中，有多少个不同的y坐标，如果询问区间跨越多个块，那么中间的整块就可以直接计算，两头零散的点暴力计算一遍即可。

//cnt[i]:纵坐标i出现的次数  lazy[i]:第i块中不同纵坐标的数量 
void add(int y)
{
	if(++cnt[y]==1)//先将该纵坐标出现次数加1 
		lazy[y/size]++;//如果次数等与1，即刚出现的纵坐标，则该块的数量加1 
}

void dec(int y)
{
	if(--cnt[y]==0)
		lazy[y/size]--;
}

//计算纵坐标 0~y 内不同的纵坐标数 
int cal(int y)
{
	int now=0;
	for(int i=0;i<y/size;i++)
		now+=lazy[i];
	for(int i=(y/size)*size;i<=y;i++)
		now+=(cnt[i]>=1);
	return now;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

由于x,y都要分块，x的最大值是n，但是y的最大值并不确定，所以为方便起见，将分块的大小固定为 $\sqrt{100000}\approx 313$，即 $size=313$。

完整代码：

//#include <bits/stdc++.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#define ll long long
#define qc ios::sync_with_stdio(false); cin.tie(0);cout.tie(0)
using namespace std;
const int MAXN = 1e5 + 7;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
int t,n,m,size,a[MAXN],cnt[MAXN],lazy[MAXN],ans[MAXN];

struct 	Query{
	int lx,ly,rx,ry,id,block;
	bool operator < (const Query& q)const
	{
		if(block!=q.block)//块号不同，按照块号排序 
			return block<q.block;
		else//块号相同 ，按照右边界x坐标排序 
			return rx<q.rx;
	}
}q[MAXN];

//cnt[i]:纵坐标i出现的次数  lazy[i]:第i块中不同纵坐标的数量 
void add(int y)
{
	if(++cnt[y]==1)//先将该纵坐标出现次数加1 
		lazy[y/size]++;//如果次数等与1，即刚出现的纵坐标，则该块的数量加1 
}

void dec(int y)
{
	if(--cnt[y]==0)
		lazy[y/size]--;
}

//计算纵坐标 0~y 内不同的纵坐标数 
int cal(int y)
{
	int now=0;
	for(int i=0;i<y/size;i++)
		now+=lazy[i];
	for(int i=(y/size)*size;i<=y;i++)
		now+=(cnt[i]>=1);
	return now;
}

int main()
{
//	freopen("in.txt", "r", stdin);
	qc;
	cin>>t;
	while(t--)
	{
		memset(cnt,0,sizeof(cnt));
		memset(lazy,0,sizeof(lazy));
	//	memset(ans,0,sizeof(ans));
		cin>>n>>m;
		size=313;//x y都要分块 根号100000 = 313
		for(int i=1;i<=n;i++)
			cin>>a[i];
		int x1,y1,x2,y2;
		for(int i=1;i<=m;i++)
		{
			cin>>x1>>y1>>x2>>y2;
			q[i].lx=x1;
			q[i].ly=y1;
			q[i].rx=x2;
			q[i].ry=y2;
			q[i].id=i;
			q[i].block=(x1-1)/size+1;
		}
		sort(q+1,q+1+m);
		x1=q[1].lx;
		x2=q[1].rx;
		//先暴力求出第一个区间的答案 
		for(int i=x1;i<=x2;i++)
			add(a[i]);
		ans[q[1].id]=cal(q[1].ry)-cal(q[1].ly-1);
		//左右指针移动 
		for(int i=2;i<=m;i++)
		{
			while(x1>q[i].lx)//l左移 
			{
				x1--;
				add(a[x1]); 
			}
			while(x1<q[i].lx)//l 右移 
			{
				dec(a[x1]);
				x1++;
			}
			while(x2<q[i].rx)//r右移 
			{
				x2++;
				add(a[x2]);
			} 
			while(x2>q[i].rx)//r左移 
			{
				dec(a[x2]);
				x2--; 
			}
			ans[q[i].id]=cal(q[i].ry)-cal(q[i].ly-1);
		}
		for(int i=1;i<=m;i++)
			cout<<ans[i]<<endl;
	}
	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110