NLP基础--single-pass 聚类算法_singlepass聚类算法

在介绍single-pass聚类方法之前，我们先来了解一下最有名的聚类算法k-means。

1. k-means聚类

所谓聚类算法是指将一堆没有标签的数据自动划分成几类的方法，属于无监督学习方法，这个方法要保证同一类的数据有相似的特征，根据样本之间的距离或者说是相似性（亲疏性），把越相似、差异越小的样本聚成一类（簇），最后形成多个簇，使同一个簇内部的样本相似度高，不同簇之间差异性高。

聚类算法有很多种（几十种），K-Means是聚类算法中的最常用的一种，算法最大的特点是简单，好理解，运算速度快。

下面来介绍一下k-means聚类算法的基本流程：

给定一个集合，集合中包含所有需要聚类的样本

1. 首先输入k的值，即我们希望将数据集经过聚类得到k个分组。
2. 从数据集中随机选择k个数据点作为初始的簇中心（质心，Centroid）
3. 对于集合中的每一个样本（除簇中心外的所有样本），计算其与每一个簇中心的距离（距离的含义有很多，后面再详细介绍），离哪个簇中心距离近，就先将该样本分为该簇。
4. 一轮迭代之后，此时集合中每个样本都属于某一个簇了。
5. 然后需要对每一个簇重新计算簇中心（通过算法选出新的质心），
   5.1 如果新的簇中心与旧的簇中心之间的距离小于某一个设置的阈值（表明重新计算的质心位置变化不大，趋于稳定，或者说收敛），可以认为我们进行的聚类已经达到期望的结果，算法终止。
   5.2 如果新的簇中心与旧的簇中心之间的距离大于设置的阈值，则需要继续迭代步骤3-5.

例子
使用一个简单的例子，来更好的理解k-means聚类算法。

现在有6个点 { p 1 , p 2 , p 3 , p 4 , p 5 , p 6 } \{p_1, p_2, p_3, p_4, p_5, p_6\} {p1​,p2​,p3​,p4​,p5​,p6​}（这6个点即为我们的样本集合），从图上看应该分成两类，前三个点一类儿，后三个点是另一类。

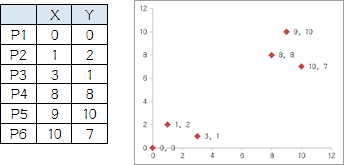
现在按照算法的步骤执行K-Means算法，体会一下过程，同时看看结果是不是和预期一致。

首先随机选出两个点作为初始的簇中心：假设选出的两个点为$p_1,p_2$
然后就需要计算集合中其他点距离这两个簇中心的距离，计算结果如下表。从表中可以看出，此时$p_3,p_4,p_5,p_6$四个点都是距离$p_2$更近一些。那么此时两个簇分别为：簇1： { p 1 } \{p_1\} {p1​}，簇2： { p 2 ， p 3 , p 4 , p 5 , p 6 } \{p_2，p_3, p_4, p_5, p_6\} {p2​，p3​,p4​,p5​,p6​}

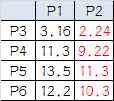
接下来就需要重新计算簇中心。簇1不需要计算，簇中心还是$p_1$，簇2有五个点，（计算新的簇中心的方法是每个点X坐标的平均值和Y坐标的平均值组成的新的点，为新的簇中心，也就是说这个新的簇中心是“虚拟的”）。因此，簇2选出新簇中心的坐标为：$p_2^{\prime }$:（（1+3+8+9+10）/5，（2+1+8+10+7）/5）=（6.2，5.6）。 综合两组，新簇中心为$p_1:(0,0)，p_2^{\prime }:(6.2,5.6)$。

再次计算各个样本到簇中心的距离 ，如下表。此时$p_2,p_3$距离簇中心$p_1$更近，而$p_4,p_5,p_6$距离簇中心$p_2^{\prime }$更近。则此时的簇1： { p 1 , p 2 , p 3 } \{p_1, p_2, p_3\} {p1​,p2​,p3​}，簇2： { p 4 , p 5 , p 6 } \{p_4, p_5, p_6\} {p4​,p5​,p6​}

接着更新两个簇的簇中心：新簇中心为$p_1^{\prime }:(1.33,1)，p_2^{\prime \prime }:(9,8.33)$。

再次计算各个样本到簇中心的距离 ，如下表。这次聚类的结果和上次没有任何变化了，说明已经收敛，聚类结束，聚类结果和我们最开始设想的结果完全一致。

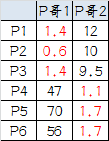
从上面的例子中可以看出k-means聚类算法的细节问题：

1. **k值如何确定。**分几类主要取决于个人的经验与感觉，通常的做法是多尝试几个K值，看分成几类的结果更好解释。
2. 初始的K个质心怎么选？ 最常用的方法是随机选，初始质心的选取对最终聚类结果有影响，因此算法一定要多执行几次，哪个结果更reasonable，就用哪个结果。 当然也有一些优化的方法，第一种是选择彼此距离最远的点，具体来说就是先选第一个点，然后选离第一个点最远的当第二个点，然后选第三个点，第三个点到第一、第二两点的距离之和最小，以此类推。第二种是先根据其他聚类算法（如层次聚类）得到聚类结果，从结果中每个分类选一个点。
3. K-Means会不会陷入一直选质心的过程，永远停不下来？ 答：不会，有数学证明K-Means一定会收敛，大致思路是利用SSE的概念（也就是误差平方和），即每个点到自身所归属质心的距离的平方和，这个平方和是一个函数，然后能够证明这个函数是可以最终收敛的函数。
4. 判断每个点归属哪个质心的距离怎么算？ 答： 第一种，欧几里德距离，这个距离就是平时我们理解的距离，如果是两个平面上的点，也就是$(x_1,y_1),(x_2,y_2)$，那这俩点距离是$\sqrt{(}{x}_1-x_2{)}^2+(y_1-y_2{)}^2$；推广到高维空间公式就以此类推。可以看出，欧几里德距离真的是数学加减乘除算出来的距离，因此这就是只能用于连续型变量的原因。 第二种，余弦相似度，余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。相比距离度量，余弦相似度更加注重两个向量在方向上的差异，而非距离或长度上。下图表示余弦相似度的余弦是哪个角的余弦，A，B是三维空间中的两个向量，这两个点与三维空间原点连线形成的角，如果角度越小，说明这两个向量在方向上越接近，在聚类时就归成一类：
   
   另外也还有很多距离度量的方法：
   
5. 还有一个重要的问题是，大家的单位要一致！ 比如X的单位是米，Y也是米，那么距离算出来的单位还是米，是有意义的 但是如果X是米，Y是吨，用距离公式计算就会出现“米的平方”加上“吨的平方”再开平方，最后算出的东西没有数学意义，这就有问题了。 还有，即使X和Y单位一致，但是如果数据中X整体都比较小，比如都是1到10之间的数，Y很大，比如都是1000以上的数，那么，在计算距离的时候Y起到的作用就比X大很多，X对于距离的影响几乎可以忽略，这也有问题。 因此，如果K-Means聚类中选择欧几里德距离计算距离，数据集又出现了上面所述的情况，就一定要进行数据的标准化（normalization），即将数据按比例缩放，使之落入一个小的特定区间。去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行计算和比较。 标准化方法最常用的有两种：min-max标准化（离差标准化）：对原始数据进行线性变换，是结果落到【0，1】区间，转换方法为 X’=（X-min）/（max-min），其中max为样本数据最大值，min为样本数据最小值。z-score标准化（标准差标准化）：处理后的数据符合标准正态分布（均值为0，方差为1），转换公式：X减去均值，再除以标准差
6. 每一轮迭代如何选出新的质心？ 答：各个维度的算术平均，比如（X1，Y1，Z1）、（X2，Y2，Z2）、（X3，Y3，Z3），那就新质心就是【（X1+X2+X3）/3，（Y1+Y2+Y3）/3，（Z1，Z2，Z3）/3】，这里要注意，新质心不一定是实际的一个数据点。
7. 关于离群值？ 答：离群值就是远离整体的，非常异常、非常特殊的数据点，在聚类之前应该将这些“极大”“极小”之类的离群数据都去掉，否则会对于聚类的结果有影响。但是，离群值往往自身就很有分析的价值，可以把离群值单独作为一类来分析。

2. single-pass 聚类

Single-pass clustering，中文名一般译作“单遍聚类”，它是一种简洁且高效的文本聚类算法。它不需要向k-means那样迭代每一个样本的状态，计算速度非常快。在文本主题聚类中，Single-pass聚类算法比K-means来的更为有效。Single-pass聚类算法不需要指定类目数量，可以通过设定相似度阈值来限定聚类数量。

Single-pass聚类算法同时是一种增量聚类算法（Incremental Clustering Algorithm），每个文档只需要流过算法一次，它可以很好的应用于话题监测与追踪、在线事件监测等社交媒体大数据领域，特别适合流式数据（Streaming Data），比如微博的帖子信息，因此适合对实时性要求较高的文本聚类场景。

处理步骤

Single-pass算法顺序处理文本，以第一篇文档为种子，建立一个新主题。之后再进行新进入文档与已有主题的相似度，将该文档加入到与它相似度最大的、且大于一定阈值的主题中。如果与所有已有话题相似度都小于阈值，则以该文档为聚类种子，建立新的主题类别。其算法流程如下：

1. 以第一篇文档为种子，建立一个主题；
2. 将文档X向量化；
3. 将文档X与已有的所有话题均做相似度计算，可采用欧氏距离、余弦距离等距离度量方法
4. 找出与文档X具有最大相似度的已有主题；
5. 若相似度值大于阈值$\theta$，则把文档X加入到有最大相似度的主题中，跳转至 7；
6. 若相似度值小于阈值$\theta$， 则文档X不属于任一已有主题， 需创建新的主题类别，同时将当前文本归属到新创建的主题类别中；
7. 聚类结束，等待下一篇文档进入

参考

1. https://www.jianshu.com/p/4f032dccdcef
2. https://zhuanlan.zhihu.com/p/74810166