算法学习——LeetCode力扣补充篇8（146. LRU 缓存、 215. 数组中的第K个最大元素、25. K 个一组翻转链表）

算法学习——LeetCode力扣补充篇8

146. LRU 缓存

146. LRU 缓存 - 力扣（LeetCode）

描述

请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类：
LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

示例

示例：

输入
[“LRUCache”, “put”, “put”, “get”, “put”, “get”, “put”, “get”, “get”, “get”]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]

解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4

提示

1 <= capacity <= 3000
0 <= key <= 10000
0 <= value <= 105
最多调用 2 * 105 次 get 和 put

代码解析

链表法（超时）

class LRUCache {
public:

    list<pair<int,int>> my_list;
    int max_size = 0;
    LRUCache(int capacity) {
        max_size = capacity;
    }
    
    int get(int key) {
        auto it = my_list.begin();
        for(int i=0 ; i<my_list.size() ;i++,it++)
        {
            if(it->first == key) 
            {
                pair<int,int> tmp = *it;
                my_list.erase(it);
                my_list.push_front(tmp);
                return tmp.second;
            }
        }
        return -1;
    }
    
    void put(int key, int value) {
        
        auto it = my_list.begin();
        for(int i=0 ; i<my_list.size() ;i++,it++)
        {
            if(it->first == key)
            {
                my_list.erase(it);
                break;
            }
        }
        my_list.push_front({key,value});
        if(my_list.size() > max_size) my_list.pop_back();
        return ;
    }
};

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache* obj = new LRUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

自制双向链表

class LRUCache {
public:
    struct  Node
    {
        int key;
        int value;
        Node* pre;
        Node* next;
        Node():key(0),value(0),pre(nullptr),next(nullptr) {}
        Node(int x,int y):key(x),value(y),pre(nullptr),next(nullptr) {}
    };

    LRUCache(int capacity) {
        _capacity = capacity;
        head = new Node();
        tail = new Node();
        head->next = tail;
        tail->pre  = head;
    }
    
    int get(int key) {
        if(my_map.find(key) == my_map.end() ) return -1;

        Node* tmp = my_map[key];
        remove_node(tmp);
        add_head(tmp);
        return tmp->value;

    }
    
    void put(int key, int value) {
         if(my_map.find(key) == my_map.end() ) //不存在
         {
             Node* new_node = new Node(key,value);
             my_map[key] = new_node;
             add_head(new_node);
             size++;
             if(size > _capacity)
             {
                 my_map.erase(tail->pre->key);
                 remove_node(tail->pre);
             }
         }else
         {
             Node* tmp = my_map[key];
             tmp->value = value;
             remove_node(tmp);
             add_head(tmp);
         }
    }
    void add_head(Node* new_node)
    {
        new_node->pre = head;
        new_node->next = head->next;
        head->next->pre = new_node;
        head->next = new_node;
    }
    void remove_node(Node* node)
    {
        node->pre->next = node->next;
        node->next->pre = node->pre;
    }
private:
    int _capacity;
    Node* head;
    Node* tail;
    int size=0;
    unordered_map<int,Node*> my_map;

};

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache* obj = new LRUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77

215. 数组中的第K个最大元素

215. 数组中的第K个最大元素 - 力扣（LeetCode）

描述

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例

示例 1:

输入: [3,2,1,5,6,4], k = 2
输出: 5

示例 2:

输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4

提示

1 <= k <= nums.length <= 105
-104 <= nums[i] <= 104

代码解析

库函数

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        sort(nums.begin(),nums.end());
        return nums[nums.size()-k];
    }
};
1
2
3
4
5
6
7

快速排序

class Solution {
public:
    void swap(int &a , int &b)
    {
        int tmp = b;
        b = a;
        a = tmp;
    }
    int part(vector<int>& nums , int left , int right)
    {
        int key = nums[left];
        while(left<right)
        {
            while(left < right && nums[right] <= key) right--;
            swap(nums[left] , nums[right]);

            while(left < right && nums[left] >= key) left++;
            swap(nums[left] , nums[right]);
        }
        return left;
    }
    void quick_sort(vector<int>& nums , int left , int right)
    {
        if(left > right) return;
        int mid = part(nums,left,right);
        quick_sort(nums,left,mid-1);
        quick_sort(nums,mid+1,right);
    }
    int findKthLargest(vector<int>& nums, int k) {
        quick_sort(nums,0,nums.size()-1);
        return nums[k-1];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

快速排序

class Solution {
public:
    void quickSort(vector<int>& arr, int left, int right) 
    {
    // 定义枢轴
    int pivot = arr[(left + right) / 2];
    //int pivot = arr[left]; 也可以
    // 定义两个指针
    int i = left;
    int j = right;
    // 当左指针比右指针小时继续循环
    while (i <= j)
    {
        // 左指针从左往右扫描，直到找到一个元素比枢轴大
        while (arr[i] > pivot) i++;
        // 右指针从右往左扫描，直到找到一个元素比枢轴小
        while (arr[j] < pivot) j--;
        // 如果两个指针没有相遇，交换它们所指向的元素
        if (i <= j)
         {
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
            i++;
            j--;
        }
    }
    // 如果左边还有元素，递归左边的排序
    if (left < j) quickSort(arr, left, j);
    // 如果右边还有元素，递归右边的排序
    if (i < right) quickSort(arr, i, right);
    
    }
    int findKthLargest(vector<int>& nums, int k) {
        quickSort(nums,0,nums.size()-1);
        return nums[k-1];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

25. K 个一组翻转链表

25. K 个一组翻转链表 - 力扣（LeetCode）

描述

给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

示例

示例 1：

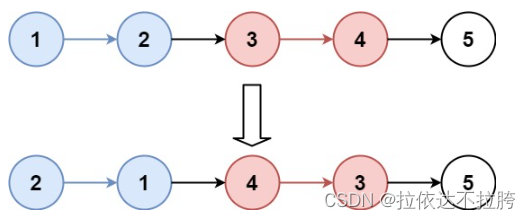
输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]

示例 2：

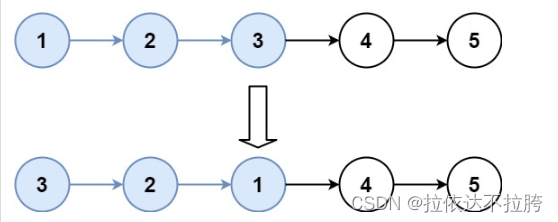
输入：head = [1,2,3,4,5], k = 3
输出：[3,2,1,4,5]

提示

链表中的节点数目为 n
1 <= k <= n <= 5000
0 <= Node.val <= 1000

进阶：你可以设计一个只用 O(1) 额外内存空间的算法解决此问题吗？

代码解析

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        stack<int> my_stack;
        vector<int> v_nums;
        ListNode* tmp = head;
        int num = 0;
        
        while(tmp != nullptr && num < k)
        {
            num++;
            v_nums.push_back(tmp->val);
            my_stack.push(tmp->val);
            if(num == k)
            {
                while(num--) v_nums.pop_back();
                num = k;
                while(num--)
                {
                    v_nums.push_back(my_stack.top());
                    my_stack.pop();
                }
                cout<<num<<' ';
                num = 0;
            }
            tmp = tmp->next;
        }
        tmp = head;
        int i=0;
        while(tmp != nullptr)
        {
            tmp->val = v_nums[i];
            tmp = tmp->next;
            i++;
        }
        return head;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48