寻找环形链表的入口点

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，我们使用整数来表示链表尾连接到链表中的位置（索引从 0 开始）。
先定义一个节点：

struct ListNode {
     int val;
     struct ListNode *next;
 };
1
2
3
4

1.判断是否为环形链表

寻找环形链表入口点的第一步，要先判断该链表是否为环形链表，环形链表的尾指针指向的位置是不确定的，可能指向首元素，这样的形成的链表环就是很大，也可能指向链表中间的随机元素，也可能指向尾节点本身，新形成的环很小。
带有环的链表如图所示：

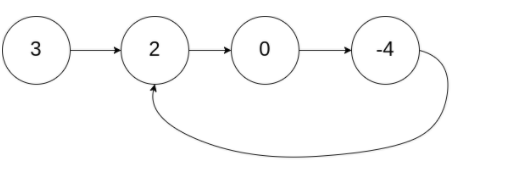
判断是否为环形链表，我们采用双指针的方法，即快慢指针，慢指针一次移动一个节点，快指针一次移动两个节点。如果该链表带环，快指针和慢指针就会在环里相遇，否则快指针就会走到尾部。判断是否带环的代码如下：
如果链表中存在环，则返回 true ，否则返回 false

bool hasCycle(struct ListNode *head) 
{
        struct ListNode* slow=head;
        struct ListNode* fast=head;
        while(fast&&fast->next)
        {
            slow=slow->next;
            fast=fast->next->next;

            if(slow==fast)
            return true;
        }
        return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

2.快慢指针延伸问题

对于以上代码我们提出两个问题；

（1）为什么slow走一步，fast走两步，他们一定会在环里相遇吗，会不会永远追不上，为什么？

答：他们一定会在环里相遇，不会追不上。
假设slow进环的时候，slow和fast的距离是N，紧接着在追击的过程中，fast往前走2步，slow往前走1步。他们每走一次，他们之间的距离聚就会缩小1.

N , N-1 , N-2…2 , 1 , 0
当N为0时slow和fast相遇。

（2）slow走1步，fast走3步行不行，走4步行不行，走x步行不行，为什么？

答：假设slow进环的是时候，fast和slow的距离是N，假设slow走1步，fast走3步。由（1）可知，在追击的过程中，fast往前走3步，slow往前走1步，他们每次之间的距离缩短2。
如果N是偶数：N , N-2 , N-4…2 , 0；则可以相遇。
如果N是奇数：N , N-2 , N-4…1 , -1；此时差距为C-1（C为环的长度），如果C-1恰好也是奇数，那么就永远也追不上。
***总结：如果slow进环时，slow和fast的差距N是奇数，且环的长度是偶数（C-1为奇数），那么他们两在环里面就会一直打圈，永远追不上。

（3）求环的入口点

假设起点到入口点的距离是L，
假设相遇点到入口点的距离是X，
假设环的大小是C

所以慢指针走的路程：L+X
快指针走的路程：L+NC+X（N为快指针在相遇之前走了多少圈，如果环很大，可能再相遇之前一圈没有走完，如果环很小，可能在相遇之前快指针已经在环里走过很多圈）
由以上可以推出：L=NC-X
***总结：一个指针从相遇点走，一个指针从起点走，他们会在入口点相遇。
找到环形链表的入口点的代码如下：

struct ListNode* detectCycle(struct ListNode* head)
{
    struct ListNode* slow = head;
    struct ListNode* fast = head;
    while (fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
        if (fast == slow)
        {
            struct ListNode* meet = fast;
            while (meet != head)
            {
                meet = meet->next;
                head = head->next;
            }
            return meet;
        }
    }
    return NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

实现如上代码，给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。