数学建模——非线性规划

目录

基本概念

凸规划

判别定理

二次规划模型

非线性规划的求解

无约束极值问题

有约束极值问题

基于求解器的解法

基于问题的求解

其他

---

非线性规划：描述目标函数或约束条件条件的数学表达式中，至少有一个是非线性函数。

基本概念

记是n维欧式空间中的一个点（n维向量），，，是定义在上的实值函数。若f,g,h函数中至少有一个是x的非线性函数，则称如下为非线性规划模型的一般形式：

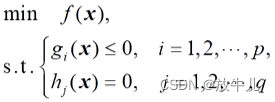
 全局最优解：若，并且都有，则称为全局最优解。

 局部最优解：x的邻域内（也包含于可行域），x所对应的函数值是最小的，则x为局部最优解。

无约束非线性规划问题可以具体表示为：

凸规划

凸规划是一类特殊的非线性规划问题，可以求得全局最优解。

凸集：

 凸函数：

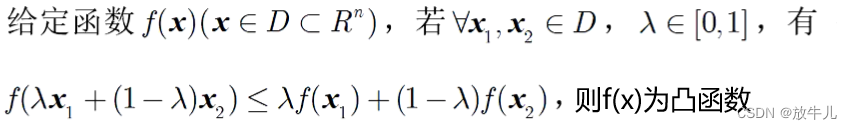
定义在凸集上的有限个凸函数的非负线性组合仍为凸函数

判别定理

半正定矩阵的行列式非负。

黑塞矩阵：

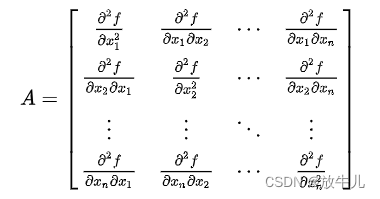
 对于非线性规划模型的一般形式，若f(x)为凸函数，g(x)为凸函数，h(x)为线性函数，则称该非线性规划问题为凸规划。凸规划局部最优解即为全局最优解，最优解的集合形成一个凸集。当目标函数为严格凸函数时，其最优解必定唯一。

例子

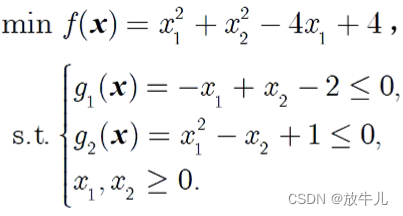
f(x)和g2(x)的黑塞矩阵的行列式：

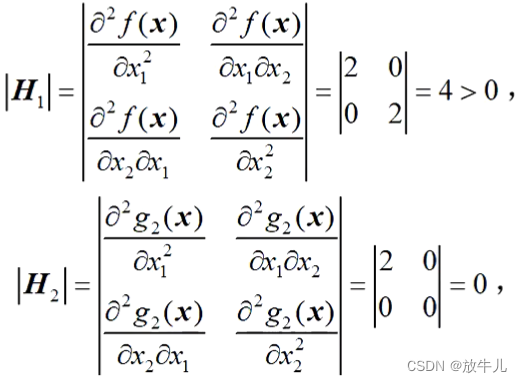
 其他约束条件为线性函数，所以是一个凸规划问题

clc,clear
prob = optimproblem;
x = optimvar('x',2,'LowerBound',0);
prob.Objective = sum(x.^2)-4*x(1)+4;
con = [-x(1)+x(2)-2 <= 0
    x(1)^2-x(2)+1 <= 0];
prob.Constraints.con = con;
x0.x = rand(2,1)%非线性规划必须赋初值，x0名字随便取
[s,f,flag,o] = solve(prob,x0);
s.x

ans =

    0.5536
    1.3064

二次规划模型

目标函数是关于决策向量的二次函数，约束条件是线性的，则该模型称为二次规划模型，一般形式：

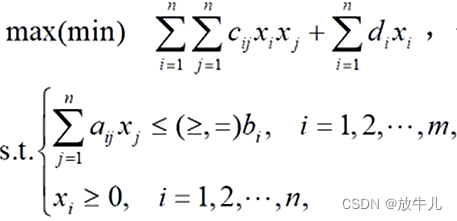
 其中：

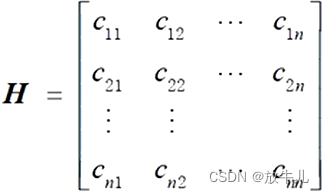
 当H正定时，目标函数最小化时，模型为凸二次规划，凸二次规划局部最优解就是全局最优解。如果不是凸规划，则建议使用fmincon函数。

例子

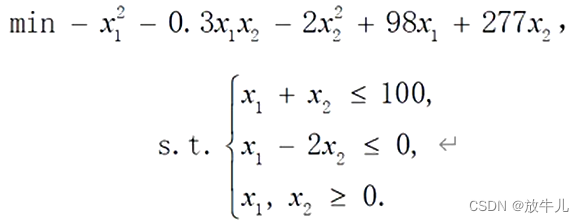
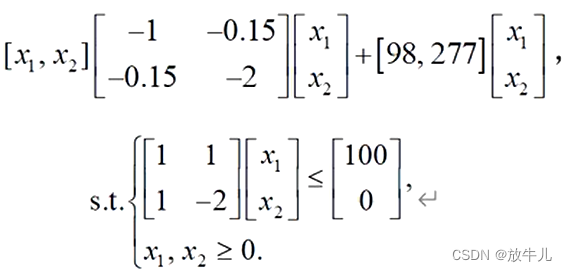
目标函数是最小化，但是H为负定矩阵，所以不是凸规划。

clc,clear
x = optimvar('x',2,'LowerBound',0);
h = [-1,-0.15;-0.15,-2];
f = [98;277];
a = [1,1;1,-2];
b = [100;0];
prob = optimproblem('Objective',x'*h*x+f'*x);
prob.Constraints = a*x <= b;
[s,f,flag,o] = solve(prob);
s.x

ans =

     1
     1

[1,1]是局部最优解，使用fmincon函数：

fx = @(x)x'*h*x+f'*x;
[x,y] = fmincon(fx,rand(2,1),a,b,[],[],[0;0],[])

x =

   1.0e-07 *

    0.2533
    0.3400
y =

   1.1901e-05

非线性规划的求解

无约束极值问题

MATLAB工具箱中用于求解无约束极小值的函数有：

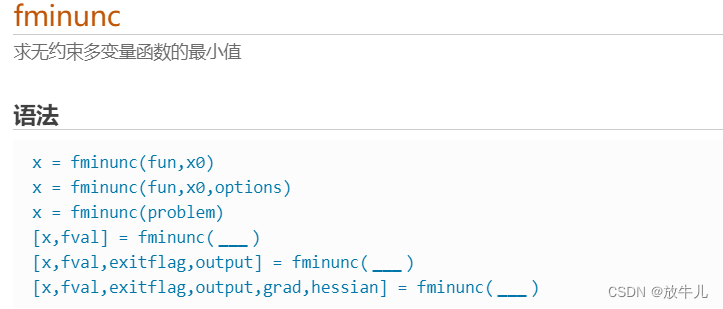
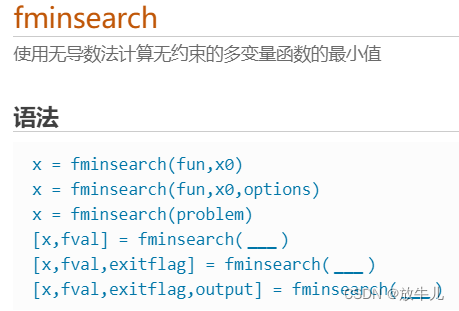
 例子

clc,clear
f = @(x) x(1)^3-x(2)^3+3*x(1)^2+3*x(2)^2-9*x(1);
g = @(x) -f(x);
[m1,n1] = fminunc(f,[0,0])%求极小值
[m2,n2] = fminsearch(g,[0,0]);%求极大值
m2,-n2

m1 =

    1.0000   -0.0000
n1 =

    -5
m2 =

   -3.0000    2.0000
ans =

   31.0000

有约束极值问题

同样有基于求解器的求解方法和基于问题的求解方法

基于求解器的解法

数学模型的标准形式为：

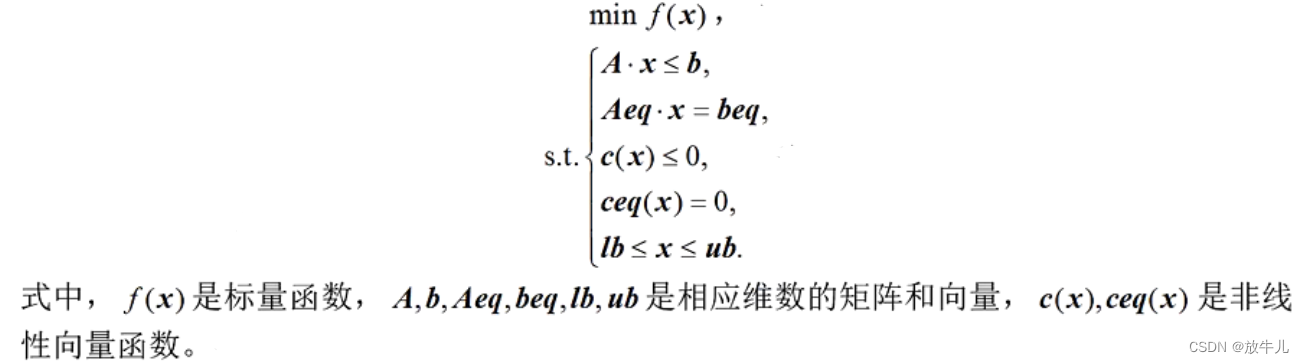
 例：

clc,clear
fun1 = @(x) sum(x.^2)+8;
[x,y] = fmincon(fun1,rand(3,1),[],[],[],[],zeros(3,1),[],@fun2)
 
function [c,ceq] = fun2(x)
c = [-x(1)^2+x(2)-x(3)^2
    x(1)+x(2)^2+x(3)^3-20];
ceq = [-x(1)-x(2)^2+2
    x(2)+2*x(3)^2-3];
end

基于问题的求解

clc,clear
x = optimvar('x',3,'LowerBound',0);
prob = optimproblem('Objective',sum(x.^2)+8);
con1 = [-x(1)^2+x(2)-x(3)^2 <= 0
    x(1)+x(2)^2+x(3)^3 <= 20];
con2 = [-x(1)-x(2)^2+2 == 0
    x(2)+2*x(3)^2 == 3];
prob.Constraints.con1 = con1;
prob.Constraints.con2 = con2;
x0.x = rand(3,1);
[s,f,flag,out] = solve(prob,x0);
s.x,f

 

其他

匿名函数的返回值只能有一个，可以是向量。