Cpp五条

这个屌丝很懒，什么也没留下！

热门标签

基于遗传算法的BP神经网络优化算法(matlab实现)_遗传算法改进前馈神经网络

作者：Cpp五条 | 2024-05-08 13:36:59

踩

遗传算法改进前馈神经网络

1 理论基础

1.1 BP神经网络概述

BP网络是一类多层的前馈神经网络。它的名字源于在网络训练的过程中，调整网络的权值的算法是误差的反向传播的学习算法，即为BP学习算法。BP算法是Rumelhart等人在1986年提出来的。由于它的结构简单，可调整的参数多，训练算法也多，而且可操作性好，BP神经网络获得了非常广泛的应用。据统计，有80??90??神经网络模型都是采用了BP网络或者是它的变形。BP网络是前向网络的核心部分，是神经网络中最精华、最完美的部分。

BP神经网络虽然是人工神经网络中应用最广泛的算法，但是也存在着一些缺陷，例如学习收敛速度太慢、不能保证收敛到全局最小点、网络结构不易确定。另外，网络结构、初始连接权值和阈值的选择对网络训练的影响很大，但是又无法准确获得，针对这些特点可以采用遗传算法对神经网络进行优化。

1.2 遗传算法的基本要素

遗传算法的基本要素包括染色体编码方法、适应度函数、遗传操作和运行参数，本案例中遗传算法部分使用Sheffield遗传算法工具箱，之前已经有详细介绍，此处不再赘述。

2 案例背景

2.1 问题描述

本节以某型拖拉机的齿轮箱为工程背景，介绍使用基于遗传算法的BP神经网络进行齿轮箱故障的诊断。统计表明，齿轮箱故障中60??右都是由齿轮故障导致的，所以这里只研究齿轮故障的诊断。对于齿轮的故障，这里选取了频域中的几个特征量。频域中齿轮故障比较明显的是在啮合频率处的边缘带上。所以在频域特征信号的提取中选取了在2、4、6挡时，1、2、3轴的边频带族fs±nfz处的幅值Ai,j1、Ai,j2和Ai,j3;,其中fs为齿轮的啮合频率，fz为轴的转频，n=1,2,3,i=2,4,6表示挡位，j=1,2,3表示轴的序号。由于在2轴和3轴上有两对齿轮啮合，所以1、2分别表示两个啮合频率。这样，网络的输入就是一个15维的向量。因为这些数据具有不同的量纲和量级，所以在输入神经网络之前首先进行归一化处理。表1和表2列出了归一化后的齿轮箱状态样本数据。

表1 齿轮箱样本数据

从表中可以看出齿轮状态有三种故障模式，因此可以采用如下的形式来表示输出。无故障：(1,0,0)。齿根裂纹：(0,1,0)。断齿：(0,0,1)。

为了对训练好的网络进行测试，另外再给出三组新的数据作为网络的测试数据，如表2所列。

表2 测试集数据

2.2 解题思路及步骤

1.算法流程

遗传算法优化BP神经网络算法流程如图1所示。

图1 算法流程

遗传算法优化BP神经网络主要分为：BP神经网络结构确定、遗传算法优化权值和阈值、BP神经网络训练及预测。其中，BP神经网络的拓扑结构是根据样本的输入/输出参数个数确定的，这样就可以确定遗传算法优化参数的个数，从而确定种群个体的编码长度。因为遗传算法优化参数是BP神经网络的初始权值和阈值，只要网络结构已知，权值和阈值的个数就已知了。神经网络的权值和阈值一般是通过随机初始化为[-0.5,0.5]区间的随机数，这个初始化参数对网络训练的影响很大，但是又无法准确获得，对于相同的初始权重值和阈值，网络的训练结果是一样的，引入遗传算法就是为了优化出最佳的初始权值和阈值。

2.神经网络算法实现

针对本章的案例，下面详细介绍BP网络算法的实现。

(1)网络创建

BP网络结构的确定有以下两条比较重要的指导原则。

①对于一般的模式识别问题，三层网络可以很好地解决问题。

②在三层网络中，隐含层神经网络个数n2和输入层神经元个数n1之间有近似关系：

本案例中，由于样本有15个输入参数，3个输出参数，所以这里n?取值为31,设置的BP神经网络结构为15-31-3,即输入层有15个节点，隐含层有31个节点，输出层有3个节点，共有15×31+31×3=558个权值，31+3=34个阈值，所以遗传算法优化参数的个数为558+34=592。使用表3-1中的9个样本作为训练数据，用于网络训练，表2中的3个样本作为测试数据。把测试样本的测试误差的范数作为衡量网络的一个泛化能力(网络的优劣),再通过误差范数计算个体的适应度值，个体的误差范数越小，个体适应度值越大，该个体越优。

神经网络的隐含层神经元的传递函数采用S型正切函数tansig(),输出层神经元的传递函数采用S型对数函数logsig(),这是由于输出模式为0-1,正好满足网络的输出要求。假定输入样本矩阵为P,创建网络可以使用以下代码：

net= newff(minmax(P),[31,3],('tansig','logsig'},'trainlm');

(2)网络训练和测试

网络训练是一个不断修正权值和阈值的过程，通过训练，使得网络的输出误差越来越小。训练函数trainlm()是利用Levenberg-Marquardt算法对网络进行训练的，通过以下代码调用函数trainlm()以及网络的参数设置：


% 训练练次数为1000,训练目标为0.01,学习速率为0.1
net.trainParam.epochs =1000;
net.trainParam.goal=0.01; 
LP.1r=0.1;
% 训练网络以及测试网络
net = train(net,P,T);

网络训练之后，需要对网络进行测试。例如测试样本数据矩阵为P_test,则测试代码如下：

Y= sim(net,P_test);

3.遗传算法实现

遗传算法优化BP神经网络是用遗传算法来优化BP神经网络的初始权重值和阈值，使优化后的BP神经网络能够更好地进行样本预测。遗传算法优化BP神经网络的要素包括种群初始化、适应度函数、选择算子、交叉算子和变异算子。

(1)种群初始化

个体编码使用二进制编码，每个个体均为一个二进制串，由输入层与隐含层连接权值、隐含层阈值、隐含层与输出层连接权值、输出层阈值四部分组成，每个权值和阈值使用M位的二进制编码，将所有权值和阈值的编码连接起来即为一个个体的编码。例如，本例的网络结构是15-31-3,所以权值和阈值的个数如表3所列。

表3 权值和阈值的个数

假定权值和阈值的编码均为10位二进制数，那么个体的二进制编码长度为5920。其中，前4650位为输入层与隐含层连接权值编码；4651～4960位为隐含层阈值编码；4961～5890位为隐含层与输出层连接权值编码；5891～5920位为输出层阈值编码。

(2)适应度函数

本案例是为了使BP网络在预测时，预测值与期望值的残差尽可能小，所以选择预测样本的预测值与期望值的误差矩阵的范数作为目标函数的输出。适应度函数采用排序的适应度分配函数：FitnV=ranking(obj),其中obj为目标函数的输出。

(3)选择算子

选择算子采用随机遍历抽样(sus)。

(4)交叉算子

交叉算子采用最简单的单点交叉算子。

(5)变异算子

变异以一定概率产生变异基因数，用随机方法选出发生变异的基因。如果所选的基因的编码为1,则变为0;反之，则变为1。

本案例的遗传算法运行参数设定如表4所列。

表4 遗传算法参数

3.matlab代码实现

完整代码可以从以下链接中获取：

基于遗传算法的BP神经网络优化算法

4.运行结果分析

输出结果如下：

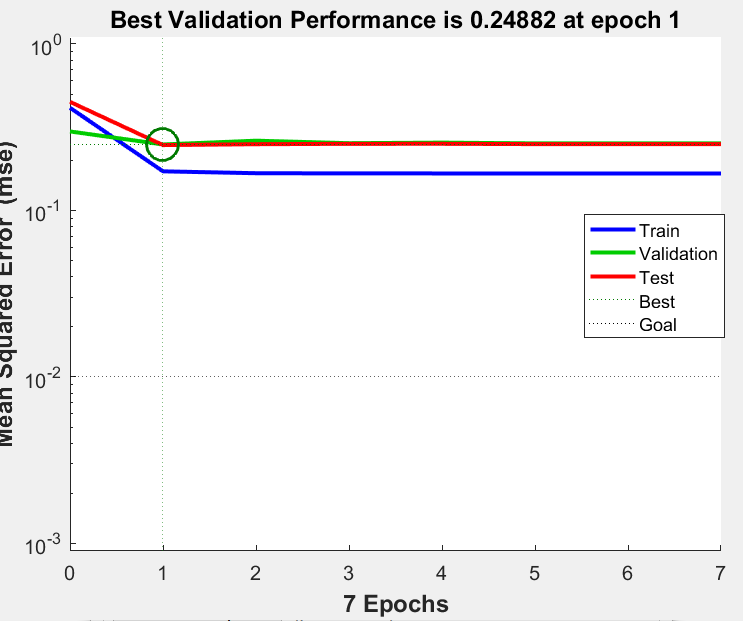
5结论

遗传算法优化BP神经网络的目的是通过遗传算法得到更好的网络初始权值和阈值，其基本思想就是用个体代表网络的初始权值和阈值，把预测样本的BP神经网络的测试误差的范数作为目标函数的输出，进而计算该个体的适应度值，通过选择、交叉、变异操作寻找最优个体，即最优的BP神经网络初始权值和阈值。除了遗传算法之外，还可以采用粒子群算法、蚁群算法等优化BP神经网络初始权值和阈值。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/Cpp五条/article/detail/554851?site