可能是最全的机器学习模型评估指标总结_balanced accuracy

目录：

• 分类模型的度量
  accuracy（准确率）
  balanced accuracy （均衡准确率）
  brier score （brier 分数）
  0-1 loss （0-1 损失）
  Hamming loss（汉明损失）
  Confusion matrix （混淆矩阵）
  precision（精确率、查准率）和 recall（召回率、查全率）
  F1_score（F1 分数）
  F${}_{\beta }$_score（F${}_{\beta }$ 分数）
  receiver_operating_characteristic_curve（ROC 曲线）
  precision_recall_curve（PR 曲线）
  cross-entropy loss（交叉熵损失）
  Hinge loss（铰链损失）
  Matthews correlation coefficient（马修斯相关系数）
  Jaccard similarity coefficients（Jaccard 相似系数）
• 回归模型的度量
  explained variance（可解释方差）
  max error（最大误差）
  mean absolute error（MAE，平均绝对值误差，l1正则损失）
  mean squared error（MSE，均方误差）
  root mean squared error（RMSE，均方根误差）
  mean_squared_log_error（MSLE，均方对数误差）
  median absolute error（中位绝对误差）
  R2（可决系数）

符号定义：

$y$：真实值，$\hat{y}$：预测值，$n$：样本数

指示函数：
1 ( x ) = { 1 x=true 0 x=false 1(x)=

$$\begin{cases} 1& \text{x=true}\\ 0& \text{x=false} \end{cases}$$ 1(x)={10​x=truex=false​

一、分类模型的度量

分类问题按照标签的属性不同一般可以分为三种：

1. binary classification 二分类：标签只有两个类别，如正类和负类。每个样本有一个标签。
2. multiclass classification 多分类：标签有多个类别，如小猫，小狗，小兔子。每个样本有一个标签。
3. multilabel classification 多标签分类：每个样本有一个或多个标签。

1.accuracy（准确率）

预测正确的样本占全部样本的比例。公式为：
$$\text{accuracy}(y,\hat{y})=\frac{1}{n}\sum _{i=1}^{n}1({\hat{y}}_i=y_i)$$

简单示例：

>>> from sklearn.metrics import accuracy_score
>>> y_true = [0, 0, 0, 0, 0, 0, 0, 1]
>>> y_pred = [0, 0, 0, 0, 0, 0, 1, 0]
>>> accuracy_score(y_true, y_pred)
0.75
1
2
3
4
5

2.balanced_accuracy （均衡准确率）

在实际场景中有时候数据集会不均衡，例如罕见疾病的预测。假设有一个包含 10000 个样本的训练集，其中正类的样本有 9900 个，负类的样本只有 100 个，如果用常规的 accuracy 度量模型的表现，可能会给出夸大的评估，表现为模型在训练集上正类负类的 accuracy 都很高，但是拿到测试集上做预测时，只有正类的 accuracy 很高，而负类的 accuracy 很低。所以引入 balanced_accuracy，它定义为每个类别中预测正确的比例的算术平均值。公式为：
$$\text{balanced-accuracy}(y,\hat{y})=\frac{1}{k}\sum _{i=1}^k\sum _{j=1}^{m_i}1(\widehat{y_{ij}}=y_{ij})$$
其中$k$为类别数，$m$为每个类别中的样本数。当数据集是均衡的时候，balanced_accuracy 和 accuracc 等价，计算的结果相同。

简单示例：

>>> from sklearn.metrics import balanced_accuracy_score
>>> y_true = [0, 0, 0, 0, 0, 0, 0, 1]
>>> y_pred = [0, 0, 0, 0, 0, 0, 1, 0]
>>> balanced_accuracy_score(y_true, y_pred)
0.42857142857142855
1
2
3
4
5

3.brier_score （brier 分数，仅用于二分类任务）

衡量模型预测的类别的概率与真实值之间的误差，它要求模型预测的结果是概率值，如 logistic 回归模型。如果把正类记作 1（也可以记作其它数值），负类记作 0，则预测的概率值介于 0 和 1 之间，越大则越可能为正类，越小则越可能为负类。brier 分数的公式为：
$$\text{brier-score}(y,p)=\frac{1}{n}\sum _{i=1}^n(p_i-y_i{)}^2$$
其中 $p$ 为模型预测的概率值。

简单示例：

>>> import numpy as np
>>> from sklearn.metrics import brier_score_loss
>>> y_true = np.array([0, 1, 1, 0])
>>> y_pred_prob = np.array([0.1, 0.9, 0.8, 0.4])
>>> brier_score_loss(y_true, y_pred_prob)
0.055
>>> # 将正类记作 0，结果是一样的
>>> brier_score_loss(y_true, 1 - y_pred_prob, pos_label = 0)
0.055
1
2
3
4
5
6
7
8
9

4.0-1 loss （0-1 损失）

表示预测值与真实值不一致的个数，公式为：
$$L_{0-1}(y,\hat{y})=\frac{1}{n}\sum _{i=1}^{n}1({\hat{y}}_i\ne y_i)$$
或
$$L_{0-1}(y,\hat{y})=\sum _{i=1}^{n}1({\hat{y}}_i\ne y_i)$$
简单示例：

>>> from sklearn.metrics import zero_one_loss
>>> y_true = [2, 2, 3, 4]
>>> y_pred = [1, 2, 3, 4]
>>> zero_one_loss(y_true, y_pred)
0.25
>>> zero_one_loss(y_true, y_pred, normalize=False)
1
1
2
3
4
5
6
7

5.Hamming loss（汉明损失）

用于多标签分类问题的模型评估。公式为：
$$\text{Hamming-loss}(y,\hat{y})=\frac{1}{n}\sum _{i=1}^n(\frac{1}{m}\sum _{j=1}^{m_i}1(\widehat{y_{ij}}\ne y_{ij}))$$
其中，m 为每个样本的标签个数。汉明距离也可以用于常规的单标签问题，即 $m=1$ 。这时候等价于 0-1 损失。

简单示例：

>>> from sklearn.metrics import hamming_loss
>>> import numpy as np

>>> # 多标签
>>> y_true = np.array([[1, 1], [1, 1]])
>>> y_pred = np.array([[0, 1], [1, 1]])
>>> hamming_loss(y_true, y_pred)
0.25

>>> # 单标签
>>> y_true = [2, 2, 3, 4]
>>> y_pred = [1, 2, 3, 4]
>>> hamming_loss(y_true, y_pred)
0.25
1
2
3
4
5
6
7
8
9
10
11
12
13
14

6.Confusion matrix （混淆矩阵）

每个类别预测正确和错误的情况。

简单示例：

>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
       [0, 0, 1],
       [1, 0, 2]])
1
2
3
4
5
6
7

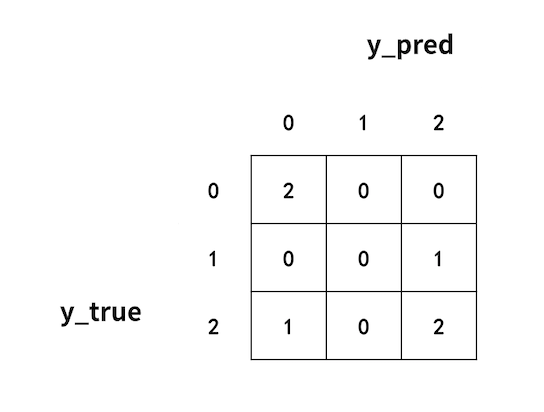
如图所示，真实值为 0，预测值为 0 的有 2 个；真实值为 0，预测值为 1 的有 0 个；真实值为 0，预测值为 2 的有 0 个，所以第一行依次为 2，0，0。第二、三行同理。

如果是二分类问题，有一种特定的记法：

• TP（true positive）：将正类预测为正类的样本数
• FN（false negative）：将正类预测为负类的样本数
• FP（false positive）：将负类预测为正类的样本数
• TN（true negative）：将负类预测为负类的样本数

混淆矩阵为：

7.precision（精确率、查准率）和 recall（召回率、查全率）

• 精确率是被预测为某一类的样本中有多少真实值也是这一类（查准）
• 召回率是所有真实值是某一类的样本中有多少被预测为这一类（查全）

在二分类问题中，一般特指正类，即：精确率是所有被预测为正类的样本中，真实值也是正类的比例，即 $\frac{TP}{TP+FP}$。召回率是所有真实值是正类的样本中，被预测为正类的比例，即 $\frac{TP}{TP+FN}$。

简单示例：

>>> from sklearn.metrics import accuracy_score, recall_score
>>> # 设1为正类
>>> y_true = [1, 1, 0, 1, 1]
>>> y_pred = [1, 0, 1, 1, 0]
>>> precision_score(y_true, y_pred)
0.6666666666666666
>>> recall_score(y_true,y_pred)
0.5
1
2
3
4
5
6
7
8

分析：TP=2，FP=1，FN=2，所以 $precision=\frac{2}{2+1}=0.6667$，$recall=\frac{2}{2+2}=0.5$。

为了扩展到多分类问题，可以使用 macro（宏平均）和 micro（微平均）。

宏平均：先对每个类别分别计算 precision 和 recall，然后对每个类别的 precision 和 recall 求算术平均，得到 macro precision 和 macro recall。

微平均：首先定义记号 T0 为 “真0”（预测值和真实值都是“0”），F0 为 “假0”（预测值是“0”但真实值不是“0”），T1 为 “真1”（预测值和真实值都是“1”），以此类推。然后对全部 Tn 求算术平均得到 T ，全部 Fn 求算术平均得到 F。最后用 T 和 F 求总体的 precision 和 recall。micro precision 和 micro recall 相等，都是 $\frac{T}{T+F}$。

简单示例：

>>> from sklearn.metrics import precision_score, recall_score

>>> y_true = [1, 1, 2, 0, 2]
>>> y_pred = [1, 0, 1, 2, 1]

>>> precision_score(y_true, y_pred, average='macro')
0.1111111111111111
>>> recall_score(y_true, y_pred, average='macro')
0.16666666666666666
>>> precision_score(y_true, y_pred, average='micro')
0.2
>>> recall_score(y_true, y_pred, average='micro')
0.2
1
2
3
4
5
6
7
8
9
10
11
12
13

分析：
宏平均：被预测为 “0” 的样本有 1 个，其中 0 个真实值是 “0”，所以 “0” 的 precision 为 0，同理可算出 “1” 的 precision 为 1/3，“2” 的 precision 为 0，它们的算术平均为 1/9=0.11111，所以 macro precision 为 0.11111。macro recall 计算方式类似，结果为 0.166666。

微平均：
T0=0，F0=1，T1=1，F1=2，T2=0，F2=1，则 T=1/3，F=4/3，所以 micro precision 和 micro recall 为 0.2。

8.F1_score（F1 分数）

通常 precision 和 recall 不能兼得，查准率高了查全率可能会偏低，查全率高了查准率可能会偏低，使用 F1 分数可以综合考虑它们二者，F1 分数是 precision 和 recall 的调和平均数（倒数平均数），将它们看成同等重要。
$$F_1=\frac{2}{\frac{1}{precision}+\frac{1}{recall}}=\frac{2\times precision\times recall}{precision+recall}$$
简单示例：

>>> from sklearn.metrics import recall_score, precision_score,f1_score
>>> # 设1为正类
>>> y_true = [1, 1, 0, 1, 1]
>>> y_pred = [1, 0, 1, 1, 0
>>> precision_score(y_true, y_pred)
0.6666666666666666
>>> recall_score(y_true, y_pred)
0.5
>>> f1_score(y_true,y_pred)
0.5714285714285715
1
2
3
4
5
6
7
8
9
10

macro F1 score：使用 macro precision 和 macro recall 计算得到的 F1。
micro F1 score：使用 micro precision 和 micro recall 计算得到的 F1。

简单示例：

>>> from sklearn.metrics import f1_score
>>> # 设1为正类
>>> y_true = [1, 1, 0, 1, 1]
>>> y_pred = [1, 0, 1, 1, 0]
>>> f1_score(y_true, y_pred, average='macro')
0.28571428571428575
>>> f1_score(y_true, y_pred, average='micro')
0.4000000000000001
1
2
3
4
5
6
7
8

9.F${}_{\beta }$_score（F${}_{\beta }$ 分数）

有时候 precision 和 recall 的重要程度是不同的，例如在广告推荐中，为了尽可能少打扰用户，更希望推荐内容是用户感兴趣的，此时查准率更重要；而在逃犯追捕中，更希望少遗漏，此时查全率更重要。$F_{\beta }$ 是 $F_1$ 的一般形式：
$$F_{\beta }=\frac{(1+{\beta }^2)\times precision\times recall}{({\beta }^2\times precision)+recall}$$
其中，$\beta >0$ 是一个自定义的参数，表示查全率对查准率的相对重要性，$\beta =1$ 时退化为标准的 $F_1$ 分数，$\beta >1$ 时查全率更重要，$\beta <1$ 时查准率更重要。

简单示例：

>>> from sklearn.metrics import fbeta_score
>>> # 设1为正类
>>> y_true = [1, 1, 0, 1, 1]
>>> y_pred = [1, 0, 1, 1, 0]

>>> fbeta_score(y_true,y_pred,beta=2)
0.5263157894736842
>>> fbeta_score(y_true,y_pred,beta=1)
0.5714285714285715
>>> fbeta_score(y_true,y_pred,beta=0.5)
0.625
1
2
3
4
5
6
7
8
9
10
11

macro $F_{\beta }$ score：使用 macro precision 和 macro recall 计算得到的 $F_{\beta }$。
micro $F_{\beta }$ score：使用 micro precision 和 micro recall 计算得到的 $F_{\beta }$。

简单示例：

>>> from sklearn.metrics import fbeta_score
>>> # 设1为正类
>>> y_true = [1, 1, 0, 1, 1]
>>> y_pred = [1, 0, 1, 1, 0]
>>> fbeta_score(y_true, y_pred, beta=2, average='macro')
0.2631578947368421
>>> fbeta_score(y_true, y_pred, beta=2, average='micro')
0.4
1
2
3
4
5
6
7
8

10.receiver_operating_characteristic_curve（ROC 曲线，仅用于二分类任务）

有些模型预测的结果是概率值，如 logistic 回归模型。将预测值与一个分类阈值比较，大于阈值则分为正类，否则为负类，这个概率预测结果的好坏决定了模型的泛化能力。根据这个概率预测结果将样本排序，最可能是正类的排在最前面，最不可能是正类的排在最后面，这样分类过程就相当于在这个排序中以某个截断点将样本分为两部分，前一部分是正类，后一部分是负类。可以根据不同的任务采用不同的截断点，如果更注重查准率，可以选择比较靠前的位置截断；如果更注重查全率，可以选择比较靠后的位置截断。

把“真正类的比例”（true positive rate，记作 TPR）作为纵坐标，“假正类的比例”（false positive rate，记作 FPR）作为横坐标作图，就得到了 ROC 曲线。
$$TPR=\frac{TP}{TP+FN}，FPR=\frac{FP}{TN+FP}$$

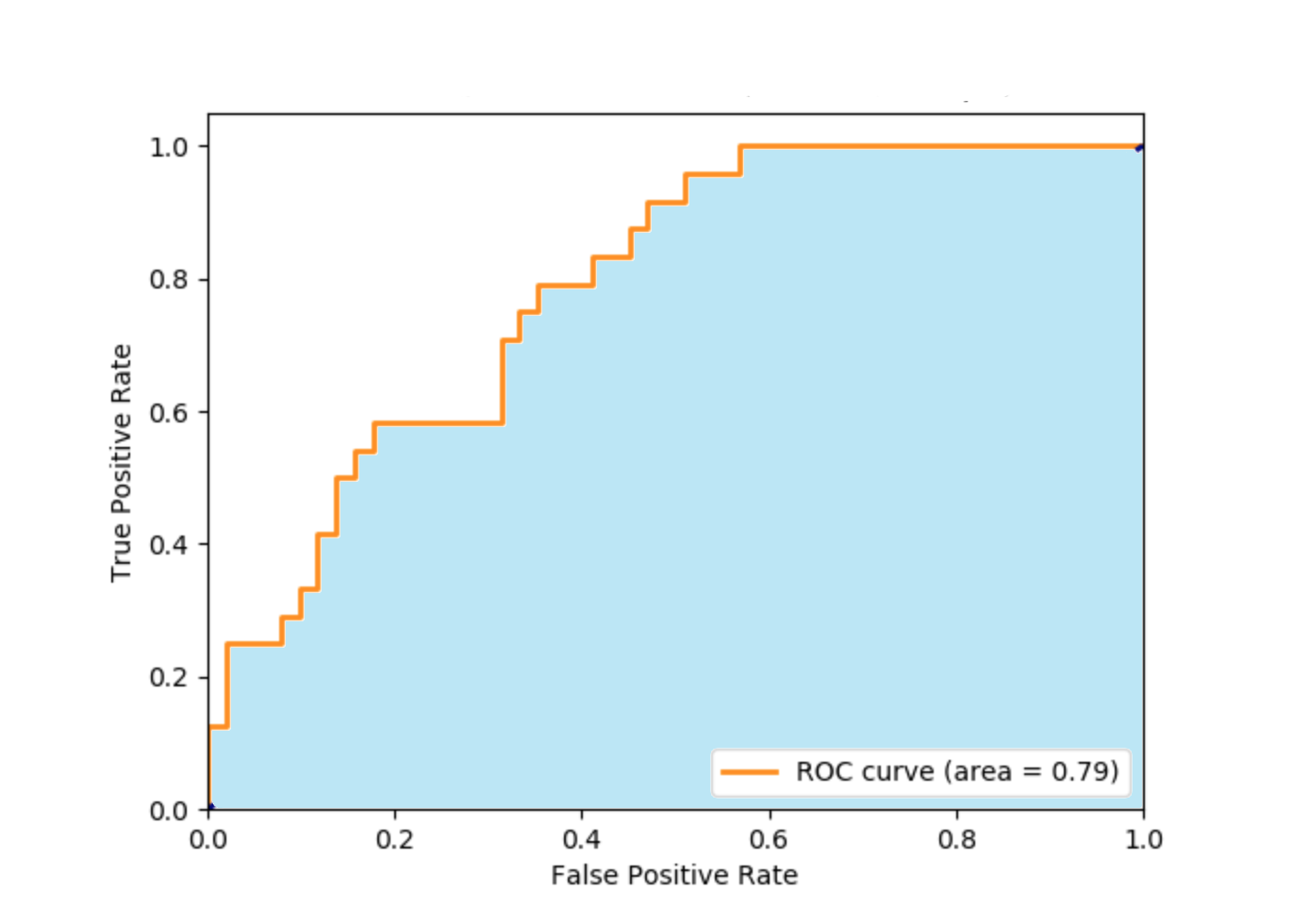
图中黄色曲线为 ROC 曲线，曲线下方的蓝色区域的面积表示了模型的分类能力，面积越大分类能力越强，这个面积叫作 Area Under ROC Curve，即 AUC。

11.precision_recall_curve（PR 曲线，仅用于二分类任务）

和 ROC 曲线类似，先根据预测的概率结果对样本排序，最可能是正类的样本在前，最不可能是正类的样本在后，然后按顺序逐个把样本作为正类进行预测，每次预测后可以计算出当前已预测的样本的查全率和查准率，以查准率作为纵坐标，以查全率作为横坐标作图，就得到了 PR 曲线。越往后，查的越全，查的越不准。

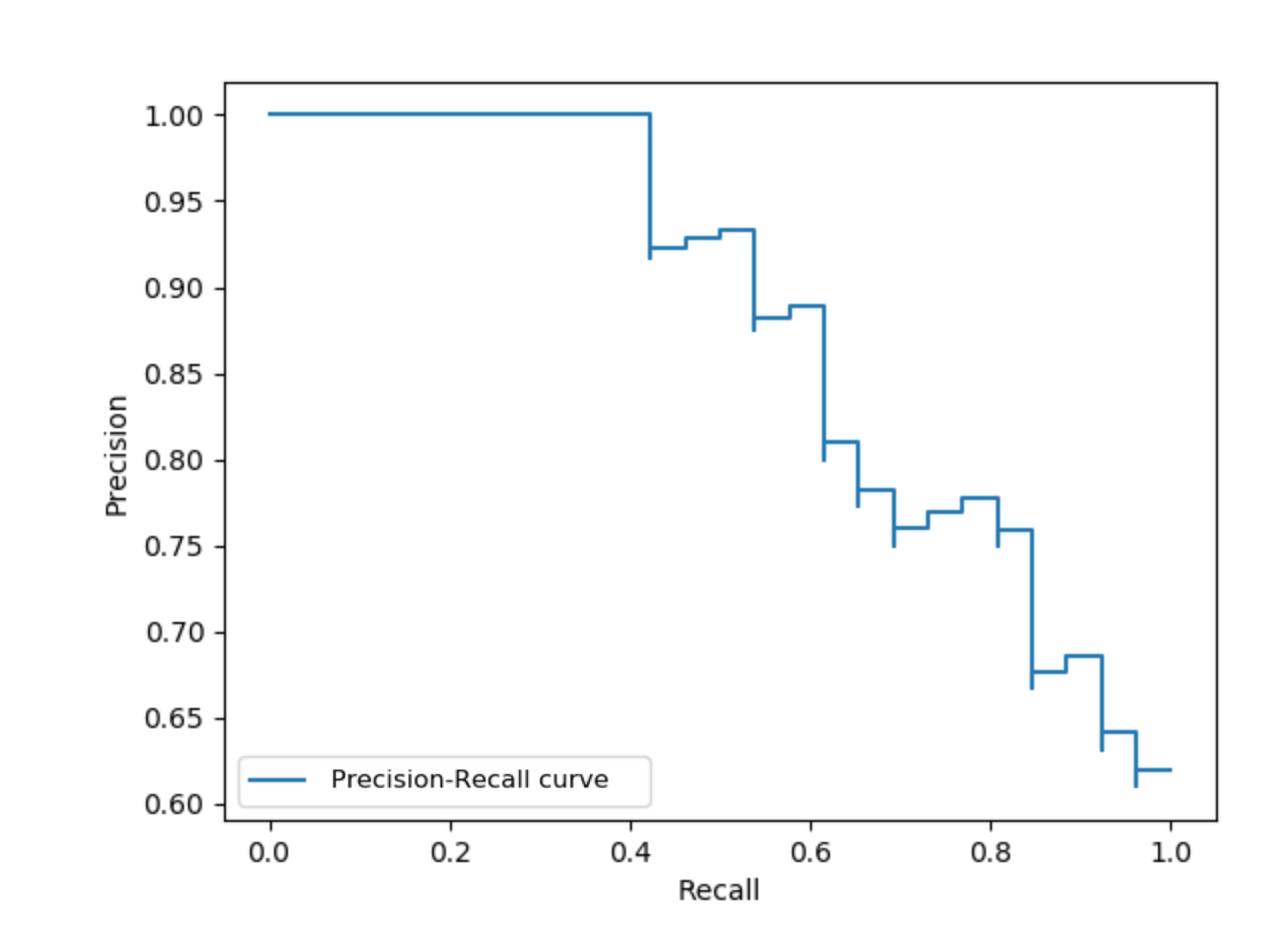
12.cross-entropy loss（交叉熵损失）

也叫 logistic regression loss，log loss，是一个概率估计的定义。通常用于 logistic 回归、神经网络和一些基于期望最大化的模型，可以用来评估预测值为概率值的模型的性能。

对于二分类问题，真实值 y ∈ { 0 , 1 } y \in \{0,1\} y∈{0,1}，预测值 $p=P(y=1)$，单个样本的交叉熵损失为 p 对 y 的条件概率的负对数。

$$L_{cross\_entropy}(y,p)=-\log \mathrm{Pr}(y|p)=-(y\log (p)+(1-y)\log (1-p))$$

对于多分类（类别总数为 k）问题，将样本标签编码为 k 维向量（one-hot）Y，模型预测样本属于每个类别的概率，组成一个概率估计矩阵 P，则公式为：
$$L_{\log }(Y,P)=-\log \mathrm{Pr}(Y|P)=-\frac{1}{N}\sum _{i=0}^{N-1}\sum _{k=0}^{K-1}{y}_{i,k}\log p_{i,k}$$

简单示例：

>>> from sklearn.metrics import log_loss
>>> y_true = [0, 0, 1, 1]
>>> y_pred = [[.9, .1], [.8, .2], [.3, .7], [.01, .99]]
>>> log_loss(y_true, y_pred)
0.1738...
1
2
3
4
5

分析：y_pred 中的第一项 [.9, .1] 表示第一个样本是 “0” 的概率是 0.9，是 “1” 的概率是 0.1。

13.Hinge loss（铰链损失）

用于最大间隔分类器，如 SVM。样本真实值 y ∈ { + 1 , − 1 } y \in \{+1,-1\} y∈{+1,−1}，模型输入为 $w$，则铰链损失为：
L Hinge ( y , w ) = max ⁡ { 1 − w y , 0 } = ∣ 1 − w y ∣ + L_\text{Hinge}(y, w) = \max\left\{1 - wy, 0\right\} = \left|1 - wy\right|_+ LHinge​(y,w)=max{1−wy,0}=∣1−wy∣+​

简单示例：

>>> from sklearn import svm
>>> from sklearn.metrics import hinge_loss
>>> X = np.array([[0], [1], [2], [3]])
>>> Y = np.array([0, 1, 2, 3])
>>> labels = np.array([0, 1, 2, 3])
>>> est = svm.LinearSVC()
>>> est.fit(X, Y)
LinearSVC()
>>> pred_decision = est.decision_function([[-1], [2], [3]])
>>> y_true = [0, 2, 3]
>>> hinge_loss(y_true, pred_decision, labels)
0.56...
1
2
3
4
5
6
7
8
9
10
11
12

14.Matthews correlation coefficient（马修斯相关系数，仅用于二分类任务）

考虑了 TP，FP，FN，TN，是一种比较平衡的度量，在数据集标签类别特别不均衡时也能使用。

二分类问题的公式为：
$$MCC=\frac{tp\times tn-fp\times fn}{\sqrt{(tp+fp)(tp+fn)(tn+fp)(tn+fn)}}.$$

对于多分类问题，首先定义：

• $t_k={\sum }_i^K{C}_{ik}$
• $p_k={\sum }_i^K{C}_{ki}$
• $c={\sum }_k^K{C}_{kk}$
• $s={\sum }_i^K{\sum }_j^K{C}_{ij}$

则公式为：
$$MCC=\frac{c\times s-{\sum }_k^K{p}_k\times t_k}{\sqrt{(s^2-{\sum }_k^K{p}_k^2)\times (s^2-{\sum }_k^K{t}_k^2)}}$$

简单示例：

>>> from sklearn.metrics import matthews_corrcoef
>>> y_true = [+1, +1, +1, -1]
>>> y_pred = [+1, -1, +1, +1]
>>> matthews_corrcoef(y_true, y_pred)
-0.33...
1
2
3
4
5

15.Jaccard similarity coefficients（Jaccard 相似系数）

本身用于二分类问题，可以通过宏平均和微平均扩展到多分类问题。

公式为：
$$J(y_i,{\hat{y}}_i)=\frac{|y_i\cap {\hat{y}}_i|}{|y_i\cup {\hat{y}}_i|}.$$

简单示例：

>>> import numpy as np
>>> from sklearn.metrics import jaccard_score
>>> y_true = np.array([[0, 1, 1],
...                    [1, 1, 0]])
>>> y_pred = np.array([[1, 1, 1],
...                    [1, 0, 0]])
>>> jaccard_score(y_true[0], y_pred[0])
0.6666...
1
2
3
4
5
6
7
8

二、回归模型的度量

1.explained_variance（可解释方差）

公式为：
e x p l a i n e d _ v a r i a n c e ( y , y ^ ) = 1 − V a r { y − y ^ } V a r { y } explained\_{}variance(y, \hat{y}) = 1 - \frac{Var\{ y - \hat{y}\}}{Var\{y\}} explained_variance(y,y^​)=1−Var{y}Var{y−y^​}​

简单示例：

>>> from sklearn.metrics import explained_variance_score
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> explained_variance_score(y_true, y_pred)
0.957...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> explained_variance_score(y_true, y_pred, multioutput='raw_values')
array([0.967..., 1.        ])
>>> explained_variance_score(y_true, y_pred, multioutput=[0.3, 0.7])
0.990...

1
2
3
4
5
6
7
8
9
10
11
12

2.max_error（最大误差）

公式为：
$$\text{Max Error}(y,\hat{y})=max(|y_i-{\hat{y}}_i|)$$

简单示例：

>>> from sklearn.metrics import max_error
>>> y_true = [3, 2, 7, 1]
>>> y_pred = [9, 2, 7, 1]
>>> max_error(y_true, y_pred)
6
1
2
3
4
5

3.mean_absolute_error（平均绝对值误差，l1 正则损失）

公式为：
$$\text{MAE}(y,\hat{y})=\frac{1}{n}\sum _{i=0}^{n-1}\left|y_i-{\hat{y}}_i\right|.$$

简单示例：

>>> from sklearn.metrics import mean_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_absolute_error(y_true, y_pred)
0.5
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> mean_absolute_error(y_true, y_pred)
0.75
>>> mean_absolute_error(y_true, y_pred, multioutput='raw_values')
array([0.5, 1. ])
>>> mean_absolute_error(y_true, y_pred, multioutput=[0.3, 0.7])
0.85...
1
2
3
4
5
6
7
8
9
10
11
12
13

4.mean_squared_error（均方误差）

公式为：
$$\text{MSE}(y,\hat{y})=\frac{1}{n}\sum _{i=0}^{n-1}(y_i-{\hat{y}}_i{)}^2.$$

简单示例：

>>> from sklearn.metrics import mean_squared_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_squared_error(y_true, y_pred)
0.375
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> mean_squared_error(y_true, y_pred)
0.7083...
1
2
3
4
5
6
7
8
9

5.root_mean_squared_error（均方根误差，l2 正则损失）

公式为：
$$\text{RMSE}(y,\hat{y})=\sqrt{\frac{1}{n}\sum _{i=0}^{n-1}(y_i-{\hat{y}}_i{)}^2}.$$

>>> from sklearn.metrics import mean_squared_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_squared_error(y_true, y_pred, squared=False)
0.612...
1
2
3
4
5

6.mean_squared_log_error（均方对数误差）

公式为：
$$\text{MSLE}(y,\hat{y})=\frac{1}{n}\sum _{i=0}^{n-1}({\log }_e(1+y_i)-{\log }_e(1+{\hat{y}}_i){)}^2.$$

简单示例：

>>> from sklearn.metrics import mean_squared_log_error
>>> y_true = [3, 5, 2.5, 7]
>>> y_pred = [2.5, 5, 4, 8]
>>> mean_squared_log_error(y_true, y_pred)
0.039...
>>> y_true = [[0.5, 1], [1, 2], [7, 6]]
>>> y_pred = [[0.5, 2], [1, 2.5], [8, 8]]
>>> mean_squared_log_error(y_true, y_pred)
0.044...
1
2
3
4
5
6
7
8
9

7.median_absolute_error（中位绝对误差）

鲁棒性更强，因为使用中位数。公式为：
$$\text{MedAE}(y,\hat{y})=\text{median}(\mid y_1-{\hat{y}}_1\mid ,\dots ,\mid y_n-{\hat{y}}_n\mid ).$$

简单示例：

>>> from sklearn.metrics import median_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> median_absolute_error(y_true, y_pred)
0.5
1
2
3
4
5

8.R2（可决系数）

公式为：
$$R^2(y,\hat{y})=1-\frac{{\sum }_{i=1}^n(y_i-{\hat{y}}_i{)}^2}{{\sum }_{i=1}^n(y_i-\bar{y}{)}^2}$$
其中 $\bar{y}=\frac{1}{n}{\sum }_{i=1}^n{y}_i$ 且 ${\sum }_{i=1}^n(y_i-{\hat{y}}_i{)}^2={\sum }_{i=1}^n{ϵ}_i^2$

简单示例：

>>> from sklearn.metrics import r2_score
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> r2_score(y_true, y_pred)
0.948...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> r2_score(y_true, y_pred, multioutput='variance_weighted')
0.938...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> r2_score(y_true, y_pred, multioutput='uniform_average')
0.936...
>>> r2_score(y_true, y_pred, multioutput='raw_values')
array([0.965..., 0.908...])
>>> r2_score(y_true, y_pred, multioutput=[0.3, 0.7])
0.925...
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17