- 1Opencv 图像金字塔----高斯和拉普拉斯_高斯拉普拉斯金字塔
- 2大数据面试系列之——Hadoop_搞定hadoop面试
- 3Oracle 11g完整安装教程_oracle11g
- 4软考-高项-关键要点整理(背诵三)_软考 质量核对单
- 5Spring Boot+VUE集成科大讯飞语音在线合成解决方案_springboot调用讯飞在线语音合成
- 6公司来了个00后,我愿称之为卷王之王,卷的让人崩溃...
- 7elment ui 组件bug总结_elementui表单的bug
- 8Flink中关于Window API 演示以及时间窗口详解_flink datastream api代对数据流设置时间滚动口,窗口大小为1分钟val windo
- 9NLTK下载使用问题_nltkdownloader教程
- 10Ubuntu16.04.06 LTS -bash 进程占用cpu很高,中了挖矿病毒_/proc/3961982/exe -> '/tmp/crond/-bash (deleted)
深圳大学算法导论实验一排序算法性能与分析
赞
踩
一.实验目的
- 掌握选择排序、冒泡排序、合并排序、快速排序、插入排序算法原理
- 掌握不同排序算法时间效率的经验分析方法,验证理论分析与经验分析的一致性。
二.实验步骤与结果
2.1 问题描述
利用选择排序、冒泡排序、合并排序、快速排序、插入排序按照升序通过给大量样本进行排序,统计不同排序算法的时间效率与输入规模的关系。
-
- 算法原理描述与核心伪代码
- 选择排序
- 算法原理描述
- 选择排序
- 算法原理描述与核心伪代码
- 从数列最左边开始,对未排序数列进行遍历,找到比其小的数并交换位置,执行一遍后找到最小的数,并向右一格继续找第二小的数。
- 全部遍历一遍后就得到最后结果。
-
-
- 核心伪代码
-
-
Select_sort(A)
for i=0 to A.length
for j=i+1 to A.length
if A[i]>A[j]
mid=A[i]
A[i]=A[j]
A[j]=mid
2.2.2 冒泡排序
2.2.2.1 算法原理描述
- 从未排序数列最左边开始,比较该位置右边是否比左边大,是则换位,否则不换。
② 如此循环遍历一遍,这样一次可以选择出一个最大的数。
③ 重复以上步骤,除了最后一个,随着循环进行,每次循环的数会越来越少,直到最后排序完成。
2.2.2.2 核心伪代码
Bubble_sort(A)
for i=0 to (A.length)-1
for j=0 to (A.length)-1-i
if A[j]>A[j+1]
mid=A[i]
A[j]=A[j+1]
A[j+1]=mid
2.2.3 插入排序
2.2.3.1 算法原理描述
① 从未排序数列第二个元素开始,向前面一一比对大小,若比该元素大,而更左边元素又比他小,则将该元素放在其之间。
② 运用上述方法完成一个循环,到最后一个元素完成时即可。
2.2.3.2 核心伪代码
Insert_sort(A)
for i=1 to A.length
aim=A[i]
for j=i-1 to 0
if aim<A[j]
A[j+1]=A[j]
else break
if aim!=A[i]
A[j+1]=aim
2.2.4 合并排序
2.2.4.1 算法原理描述
①运用递归将数组不断地二分,直到只剩一个元素为止。
②在最后一个二分所得数字进行排序,然后合并进入上一个二分步骤,与另一个元素进行排序。
③如此一直递归到最开始的时候,由于有两个数组没排序,各自将最左边元素比较,小的元素提取出来放到一个新数组。
④到后面会出现只剩一个数组,另一个数组没元素的情况,此时将剩下数组放入新数组,排序即完成
2.2.4.2 核心伪代码
Divide(A,left,right)
If left == right
Return
If left < right
mid=(left+right)/2
Divide(A,left,mid)
Divide(A,mid+1,right)
Combine(A,left,right)
Combine(A,left,right)
Left0=left
mid=(left+right)/2
midr=mid+1;
While left<=mid and k<=right
If A[left] < A[midr]
B[i++]=A[left++]
Else
B[i++]=A[left0++]
If left > mid
For midr to right
B[i++]=A[midr]
If midr>right
For left to mid
B[i++]=A[left]
For j=0 to A.length
A[left0++]=B[j]
2.2.5 快速排序
2.2.5.1 算法原理描述
① 先将第一个元素数值保存,将未排序数组的第一个元素当做排序目标,从最右边往前开始遍历,若有小于第一个元素的则替换,然后从左边开始遍历,找到比最右数值大的,然后进行替换。
② 安装上述操作一直循环,最后会指向中间或者超过中间,此时位置即为第一个元素的位置。
③ 重复上述操作,不断递归直到最后即可。
2.2.5.2 核心伪代码
Quick_sort(A,left,right)
If left<right
i=left
j=right
x=A[left]
while i<j and A[i]<A[j]
j--;
if A[j]<=A[i]
A[i++]=A[j]
while i<j and A[i]<A[j]
i++
if A[i]>=A[j]
A[j--]=A[i]
A[i]=x;
Quick_sort(A,left,i-1)
Quick_sort(A,i+1,right)
2.3 算法测试结果及效率分析
2.3.1 选择排序结果分析
| 数组长度 | 10000 | 20000 | 30000 | 40000 | 50000 |
| 排序方法 | |||||
| 选择排序 | 14.65 | 60.55 | 144.95 | 244.3 | 391.4 |
表2.3.1.1
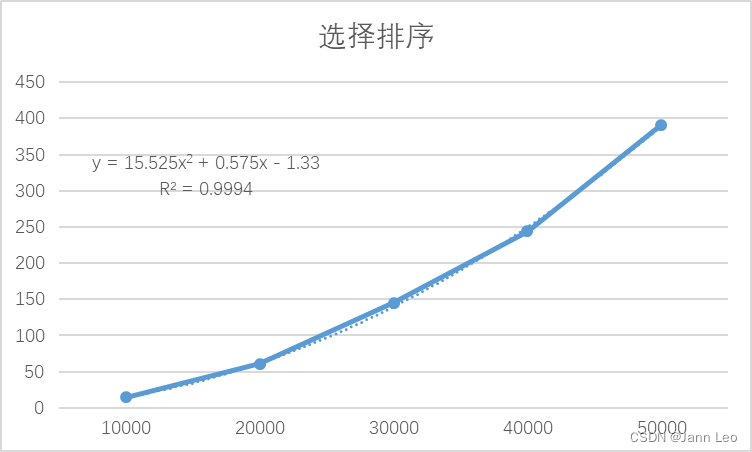
图2.3.1.1
2.3.1.1 算法复杂度理论分析:
每次循环分别比较N-1次,N-2次,N-3次,……,共比较的次数是 (N - 1) + (N - 2) + ... + 1。求和,得N(N-1)/ 2,其时间复杂度为 O(N2)。
-
-
-
- 结果分析:
-
-
图2.3.1.2中使用2阶多项式函数拟合,可决系数R^2高达0.9994,表明实测值和理论分析的变化趋势几乎相同。
2.3.2 冒泡排序结果分析
| 数组长度 | 10000 | 20000 | 30000 | 40000 | 50000 |
| 冒泡排序 | 12.75 | 58.45 | 138.8 | 246.9 | 389.05 |
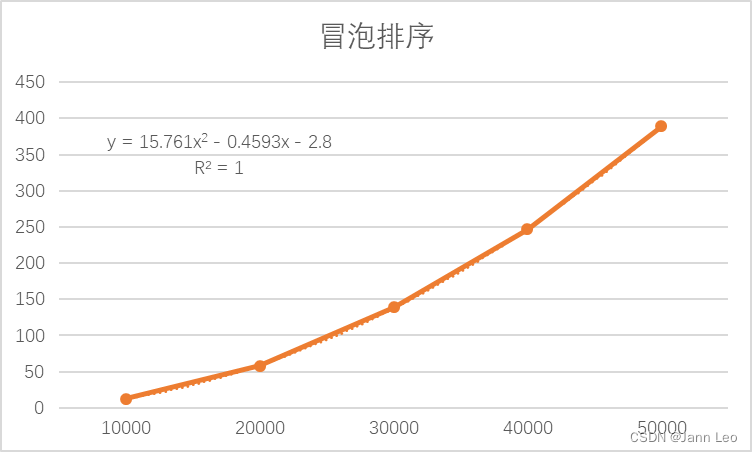
图2.3.2.2
2.3.2.1算法复杂度理论分析:
若不考虑优化的情况,则外层循环执行 N - 1次,内层循环最多的时候执行N次,最少的时候执行1次,平均执行 (N+1)/2次,一共执行 (N - 1)(N + 1) / 2 = (N^2 - 1)/2次,故复杂度为O(N^2)。
2.3.2.2结果分析:
图2.3.2.2中使用2阶多项式函数拟合,可决系数R^2高达1,表明实测值和理论分析的变化趋势完全相同。
2.3.3 插入排序结果分析
| 数组长度 | 10000 | 20000 | 30000 | 40000 | 50000 |
| 插入排序 | 5.2 | 15.75 | 39.45 | 65.95 | 109.8 |
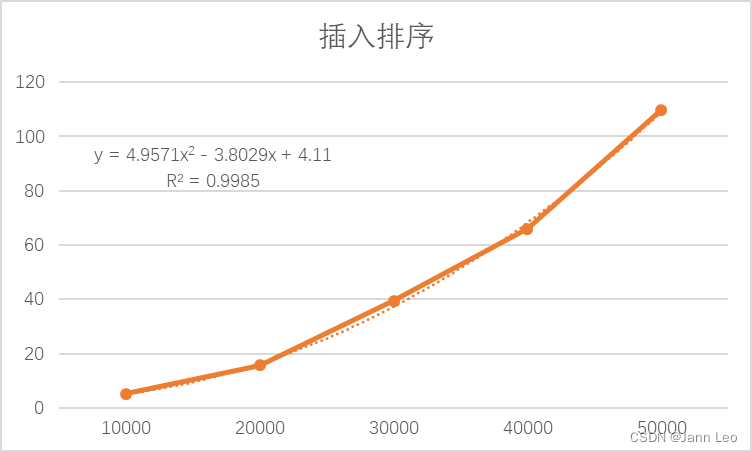
图2.3.3.1
2.3.3.1算法复杂度理论分析:
最优的情况:当待排序数组完全有序时,只需当前数跟后一位数比较一次即可,一共需要要比较N-1次,时间复杂度:O(N)
最坏的情况:待排序数组是逆序的,此时需要比较总次数为1+2+3+…+N-1的求和,所以,插入排序最坏情况下的时间复杂度:O(N2)
现实情况往往是最优与最坏情况取平均,A[1..j-1]中的一半元素小于A[j],一半元素大于A[j],故平均时间复杂度依然为O(N2)
2.3.3.2结果分析:
图2.3.3.1中使用2阶多项式函数拟合,可决系数R^2高达0.9985,表明实测值和理论分析的变化趋势几乎相同。
2.3.4 合并排序结果分析
| 数组长度 | 10000 | 20000 | 30000 | 40000 | 50000 |
| 排序方法 | |||||
| 合并排序 | 0.1 | 0.15 | 0.3 | 0.35 | 0.6 |
| log10(t) | -1 | -0.82391 | -0.52288 | -0.45593 | -0.22185 |
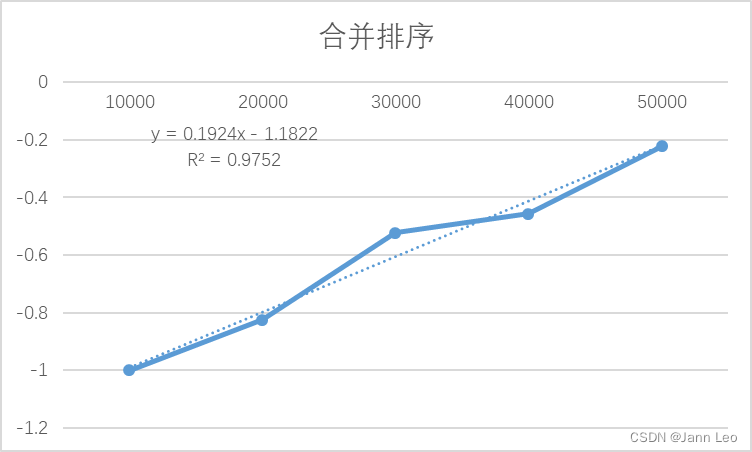
2.3.4.1算法复杂度理论分析:

从这个递归树可以看出,第一层时间复杂度为O(n),第二层时间复杂度为O(n/2+n/2)=O(n),不难发现往下每层代价均为n。共有[log10n]+1层,故总的时间代价为n*(log10n+1),时间复杂度是O(nlog10n)
2.3.4.2结果分析:
从图中可以看出对于5万以内的数据,归并排序可在一秒之内,而曲线存在波动,推测是因为对于归并排序来说,万级数据规模太小,运行时间太短,导致数据量变化对实验结果影响没有实验环境带来的扰动大,所以对实验环境带来的扰动非常敏感。
2.3.5 快速排序结果分析
| 数组长度 | 10000 | 20000 | 30000 | 40000 | 50000 |
| 排序方法 | |||||
| 合并排序 | 0.1 | 0.25 | 0.55 | 0.9 | 1 |
| log10(t) | -1 | -0.60206 | -0.25964 | -0.04576 | 0 |
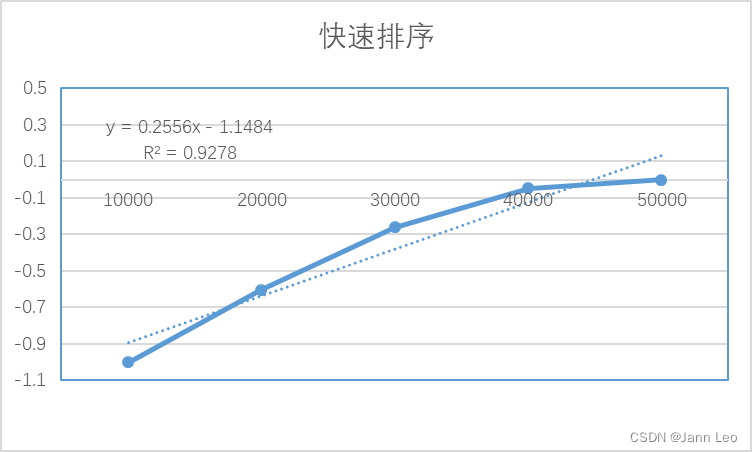
2.3.5.1算法复杂度理论分析:
在最优情况下,左子树和右边子树严格二分,递归树的深度为log2n + 1,即仅需递归log2n次,需要时间为T(n)。此时分析过程与归并排序相同,时间复杂度为O(nlog10n)
在最坏的情况下,待排序的序列为正序或者逆序,递归树为长为n的直线。所以需要递归n‐1次,每次比较次数为N - 1次,N-2次,N-3次,……,共比较的次数是 (N - 1) + (N - 2) + ... + 1。求和,得N(N-1) / 2,其时间复杂度为 O(N2)。
易知,平均的情况时间复杂度为O(nlog10n)
2.3.5.2结果分析:
和归并排序情况一样,曲线存在波动,推测是由于数据规模太小,运行时间太短,当数据比较小时即使偏差很小表现出来的误差还是很大,对实验环境带来的扰动非常敏感。推测原因是快排本身对数据的起始排列顺序等因素很敏感,有时可能遇到递归树失衡的情况。
在代码中分别以t=10000 20000 30000 40000 50000 随机产生相应数量的数字元素,并对各种算法进行测试,得到如下运行时间表:
表2.3.1.1 各个算法运行时间表(ms)
| t\ms | 冒泡排序 | 选择排序 | 插入排序 | 快速排序 | 合并排序 |
| 10000 | 12.75 | 14.65 | 5.2 | 0.1 | 0.1 |
| 20000 | 58.45 | 60.55 | 15.75 | 0.25 | 0.15 |
| 30000 | 138.8 | 144.95 | 39.45 | 0.55 | 0.3 |
| 40000 | 246.9 | 244.3 | 65.95 | 0.9 | 0.35 |
| 50000 | 389.05 | 391.4 | 109.8 | 1 | 0.6 |
由表2.3.1.1 可作出效率曲线图如下:
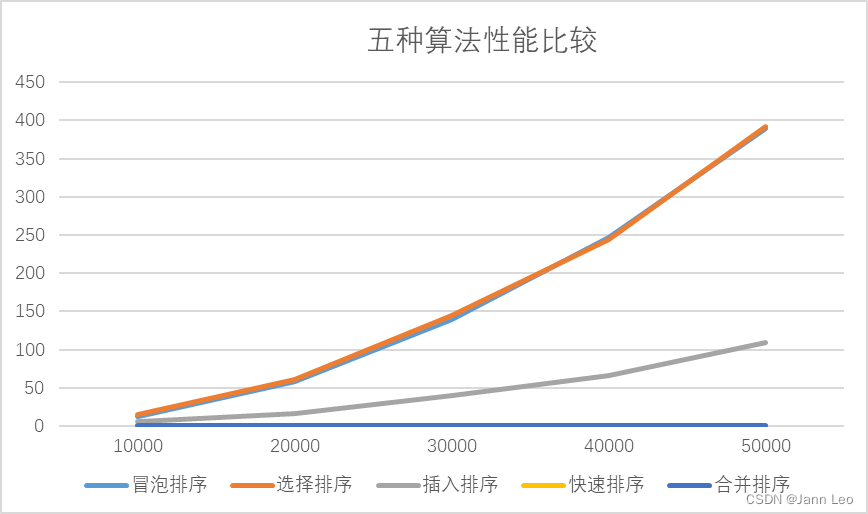
三.实验心得
通过本次实验,加深了我对排序算法的认识,学习了快速排序、合并排序、插入排序等新的排序方法,同时也学习了通过理论和实测分析算法的时间效率,验证了理论分析与经验分析的一致性。
同时,在进行算法设计中,对于随机数来说,在计算机中没有可以生成完全随机数的方法,在使用rand()函数进行取数时,如果数目想等的话,取出来的数就是相同的,导致20次不同数据的排序计算要求就达不到,所以提前了解rand函数的机制很重要。


