路径规划算法_j路径规划算法

一、Dijkstra算法

求解单源最短路径的非常经典的一种算法，是基于贪心思想实现的，用于计算一个节点到其他节点的最短路径，即从起始点为中心向外层层扩展（广度优先搜索思想），直到扩展到终点为止。

基本步骤是：首先将起始点到所有点的距离记录下来（能直接到达的点的距离为相对应的值，不能直接到达的点的距离为无穷），找到其中最短的距离，然后到达那个点，更新这个新到达的点到其他点的距离，继续重复操作，直到终点。

二、Floyd算法

求解任意两点之间的最短路径问题，由于每次先将中间节点作为当前节点进行考虑，再按照不同的中间节点进行循环，所以被称为多源最短路径算法。求解过程主要是先准备2维数组，一个一个点的加入，然后去修改权重，最后得到结果，如果顶点多的话会比较麻烦。下面这篇博客的实例讲得比较清楚。

最短路径之Floyd(弗洛伊德)算法，以及显示完整路径_floyd最短路径算法-CSDN博客

三、A*算法

是一种启发式搜索算法，结合了Dijkstra算法的广度优先搜索和启发式函数的评估，以提高搜索效率。

启发式搜索是利用启发函数来对搜索进行指导，从而实现高效的搜索。

基本概念：

1. 节点评估：每个节点都有一个估价函数，用于评估该节点到目标节点的距离。这个估价函数通常使用启发式函数来估计距离，例如曼哈顿距离或欧几里得距离；
2. 开放列表和关闭列表：A*算法使用两个列表来跟踪搜索过程中的节点。开放列表存储待扩展的节点，关闭列表存储已经搜索过的节点；
3. 估价函数和总代价：每个节点都有一个估价函数值，表示从起始节点到该节点的估计代价。总代价则是节点的估价函数值加上从起始节点到该节点的实际代价；
4. 启发式搜索：A*算法在扩展节点时，选择总代价最小的节点进行扩展。这样可以优先选择路径估计最优的节点，以期望更快地找到最短路径；
5. 路径重构：一旦找到目标节点，A*算法可以通过回溯父节点的方式，从目标节点开始重构最短路径。

 A*算法通过F = G + H 来计算每个节点的优先级。

其中：

• F是节点n的综合优先级（即该点的总耗费）。当我们选择下一个要遍历的节点时，我们会选择优先级最高（即值最小）的节点；
• G是节点n距离起点的代价；
• H是节点距离终点的预计代价，也就是A*算法的启发函数。

基本流程：

1. 起始节点加入开放列表，并设置其 g(n) 值为0。
2. 当开放列表不为空时，重复以下步骤：（开放列表就是放还没有走过的点，不为终点就可以找）
3. 从开放列表中选择 f(n) 值最小的节点 n。（即优先级最高的点）
4. 将节点 n 从开放列表中移除，并加入关闭列表。（说明这个点走过了）
5. 如果节点 n 是目标节点，算法终止，路径找到。
6. 对于节点 n 的所有相邻节点 m，执行以下操作：
7. 如果节点 m 不在开放列表和关闭列表中，将节点 m 加入开放列表，并计算它的 g(m) 和 h(m) 值。
8. 如果节点 m 已经在开放列表中，比较新的 g(m) 值与当前 g(m) 值的大小，选择更小的值作为 g(m)，并更新节点 m 的父节点为节点 n。
9. 如果节点 m 已经在关闭列表中，比较新的 g(m) 值与当前 g(m) 值的大小，选择更小的值作为 g(m)，并重新将节点 m 加入开放列表。

A*算法的难点在于估价函数的设置。 

四、D*算法 

D*算法是增量式路径规划算法，是A*算法的扩展，可以在动态环境中更新和重新规划路径，有效地应对环境状态的变化。类似的是，D*算法通过维护一个开放队列（Openlist）来对场景中的路径节点进行搜索；不同的是，D*算法不是从起始点开始，而是从目标开始，不断向起始点方向搜索路径，并根据环境的变化动态更新路径。

增量式搜索是对以前的搜索结果信息进行再利用来实现高效搜索，大大减少搜索范围和时间。

D*算法采用反向搜索的目的在于后期需要重新规划路径的时候，能够用到先前搜索到的最短路径信息，减少搜索量。因为以目标向起始点进行搜索得到的最短路径图，是以目标点为中心辐射出的最短路径图，图上目标点到各点之间都是最短路径，为此其在既定路径上遇到问题需要重新路径规划的时候，可以很好的利用原先得到的信息。而以起始点向目标搜索得到的最短路径图是以起始点为中心辐射出的最短路径图，当沿着既定路径前行遇到障碍物之后，需要重新进行路径规划时，没有办法很好的利用原先搜索得到的信息。

我的理解是，如果给无人机做路径规划的时候，无人机突然遇到一个障碍物挡住了现在正在前进的路，那他就要重新计算一遍A*，但D*就能解决这个问题。它是最开始的静态环境中找到目标路径后，将搜索过程记录下来，之后在遇到障碍物的时候，就能通过之前的保存下来的信息快速规划出新的路径。

基本概念：

1. 基于图的路径规划： D* 算法将路径规划问题抽象为一个有向图，图的节点表示位置或状态，图的边表示连接两个节点的可能移动或转换方式；
2. 状态和代价： 每个节点都有一个状态和对应的代价值。状态表示节点在环境中的位置或状态信息，代价值表示到达该节点的成本，通常使用距离或时间作为代价；
3. 开放列表（Openlist）：存储待扩展的节点；
4. 代价图（Costmap）：存储每个节点的当前代价值；
5. 局部更新： D* 算法通过局部更新操作来快速响应环境的变化。当环境发生变化时，只需要更新与变化相关的节点和边的代价，而不必重新计算整个路径；
6. 反向搜索： D* 算法使用反向搜索来更新路径和代价信息。通过从目标节点开始反向搜索，沿着当前路径反向更新每个节点的代价值，使得路径适应环境变化；
7. 重规划： 当环境状态发生变化时，D* 算法会重新规划路径。它从起始节点开始，通过局部更新和反向传播逐步更新路径和代价信息，直到找到一条新的最短路径。

基本流程： 

1. 初始化：将终点作为当前节点，将起点的代价f(x)置为0；
2. 扩展节点：从当前节点开始向相邻节点搜索路径，计算路径的代价，更新相邻节点的代价和f(x)值；
3. 路径更新：如果某个节点的代价发生变化，就更新它的相邻节点的f(x)值，并将它们添加到路径列表中；
4. 重复步骤2和3，直到找到起点为止。

与A*算法的比较：

D*算法分为两个阶段，第一个阶段是使用Dijkstra/A*算法找到从目标点到起始点的静态可行路径，然后机器人开始从起点向目标点运动。第二个阶段是动态避障搜索阶段，主要用于修正若干个受障碍物影响而导致价值发生变化的那些节点信息。

在初始化的时候：D*算法是将目标点放入Openlist中，而A*算法是将起始点放到Openlist中。

之后在搜索的过程中：

1.D*算法是从Openlist中找到K值最小的节点，并将该节点从Openlist 中移除，并放到Closelist列表中；而A*是从Openlist中找到F值(F=G+H)最小的节点进行拓展。

K值是什么？在D*算法中是从目标点向起始点进行搜索，我们将从目标点到当前点的代价记为H（其实从原理上来看与这里的H与A * 中 的G更为相似，都是从搜索开始的点到当前点累计的代价值），在D*中没有使用从当前点到起始点的估计值，也就是没有使用启发信息，从这一点上来看，D*与Dijkstra算法更为相似。D*是针对动态环境设计的算法，由于环境的改变某点处的H值可能发生改变，而某点处的K值其实记录的就是该点的最小H值 ，也就是说，对于还未遍历到的点，K=H=inf；对于标识为open或closed的点，K=min {K , H_new}。

思考：为什么不选用最小的H值节点来作为拓展点，而是使用K值呢？

动态环境下，假如某个节点变成了障碍物，此时其H值会被修改为inf，我们需要将这种变化传递下去，若采用H值作为选取标准，该节点会被置于openList中的最后。也就是说，此时路径规划会从openList中剩余的处于OPEN状态的节点开始，一直扩张至全图都没有不可达节点之后，才会访问该节点。这显然并不合理，因为我们的目的就是要在节点状态动态变化的时候减少搜索的空间，提高搜索效率。 而用最小的H值也就是K值在openList中进行排序，表示这里曾有一条捷径，那么就会优先在这附近进行搜索。

 2.判断当前拓展点的K值是否与该点的H值相同。

在D*算法中每个节点还有Lower态和Raise态两种状态，若H=K，记为Lower态﹔若H>K,记为Raise态，当该节点处于Raise态时表明有更优的路径。

（1）若K < H，说明该节点已经受到了动态障碍物的影响，那么就遍历该节点的相邻节点，看是否能够以某个相邻节点作为父节点，来使该节点的H值减小。我们用x表示该节点，用y表示其某个相邻节点，即若H(y) < K(x),且H(x) > H(y) + C(y ,x),则将当前点x的父节点改为y，并将该点的H值更改为H(x) = H(y) + C(y ,x)，其中C(y ,x)代表从y点到x点的代价值。

（2）若K = H，则按照以下准则进行节点的拓展：遍历每个相邻节点，若出现以下三种情况之一，则将该相邻节点的父节点设为当前点，并将该相邻节点的H值设为H(x) + C(x,y)，放到OpenList中。

   ①若该相邻节点从未被拓展过，即该相邻节点还未进OpenList；

   ②若该相邻节点的父节点是当前点，且H(y) ≠ H(x) + C(x,y)；

   ③若该相邻节点的父节点不是当前点，且H(y) >  H(x) + C(x,y)。

以上三种情况中，情况①和③与 A*算法的拓展方式相同，较容易理解，而第②种情况，是D*算法考虑动态障碍物后新增的，我们可以这样理解，该相邻节点的父节点是当前点，也就是说正常情况下H(y) = H(x) + C(x,y)，而此时不等于则说明，环境已经发生了改变，使得H(x)变大了，所以相应的由x点拓展出来的子节点y的H值也要进行更新，并将其重新放到OpenList中，对由y拓展出来的点进行更新，以此更新下去。

（3）执行完K < H之后再判断K是否=H，若还是不等，则按照以下准则进行节点的拓展：

   ①该相邻节点从未被拓展过，即该相邻节点还未进OpenList；

        ②该相邻节点的父节点是当前点，且H(y) ≠ H(x) + C(x,y)， 若该相邻节点y是以上两种情况，则将该相邻节点的父节点设为当前点，并将该相邻节点的H值设为H(x) + C(x,y)，放到OpenList中。

   ③若该相邻节点的父节点不是当前点，且H(y) > H(x) + C(x,y)，则将当前点x加入到OpenList。

这里为什么不将y的父节点设定为当前点x，并对其H(y)进行更新呢？往OpenList里面放到为什么不是y，而是x呢？

此时的当前点x处于Raise态，即当前x处的代价值不是最优的，所以，我们将x放到OpenList中，等待下一次循环，当前点的代价值变成最优的后，再对该相邻节点进行处理，以此来保证传递下去的代价值是最小的。

   ④若该相邻节点的父节点不是当前点，且H(x) > H(y) + C(x,y)，且该相邻点y在closedlist中，且H(y) > K，则将y重新放到OpenList中。

怎么理解呢？ 我们每次从OpenList取点时，取的是K最小的，既然y已经在closedlist中，说明y比当前点先拓展，即K(y) <= K(x)，而现在H(y) > K(x)，说明y受到了障碍物的影响，使得H(y)变大了，因此需要将y放到OpenList进行考察。

3.循环往复，拓展后通过路径回溯找到所需的路径。

4.如果按照规划的路径进行移动的过程中，若当前点为x，且探测到要走的下一个节点y存在障碍，或者节点y本来存在障碍物，但是继续行进到x的时候，障碍物被移除。这时就要调用modify_cost(x,y,val)函数，将最新的cost(x,y)以及H(y)的值进行变更，若此时x已经位于closedlist，则需要将其重新放到openlist中，并反复执行process_state()函数用于传播节点h值变更信息和路径搜索直到process_state()函数返回的openList中所有节点的K值中的最小K值(K_{min}) >= H(x) 或者openList没有任何节点时，表示重新路径规划完成，或者无法找到别的路径从x点规划到目标点G。

思考：为何重新进行路径规划的时候，当执行到 (k_{min}) >= h(y) 时停止？

因为process_state()函数的功能是用邻居节点来减低自身节点的H值的，当所有处于OPEN状态的节点中的K值的最小值 (K_{min}) 也要大于等于H(y)时，表示不可能再通过process_state()函数的执行来降低H(y)值了，那么自然就没有再搜索的必要，且已经完成了路径的修正。

相关资料：

D-star算法简介及相关思考_d星算法-CSDN博客

D*算法详解 一看就会 手把手推导 完整代码注释 - 知乎 (zhihu.com)

D star路径搜索算法_dstart 算法详解-CSDN博客

数学建模6——路径规划的各种算法(Dijkstra、Floyd、A*、D*、RRT*、LPA*)_路径规划算法分类-CSDN博客

D*算法原理与程序详解（Python）-CSDN博客

如果目标点的位置不断发生变化，D*算法的使用需要进行一些调整，可能要将移动后的位置添加到地图中，并更新所有受影响的路径节点，重新计算最短路径。

或者预测目标点的位置，预测其在未来一点时间内的移动轨迹？

还有一种方法是使用动态窗口法，将搜索窗口动态地调整到目标点当前地位置，并在这个窗口内进行路径搜索。

五、RRT算法 

如果目标点的位置一直在变化，RRT算法可能更适合用在这种情景下。

RRT算法是一种基于采样的路径规划算法，全称是快速扩展随机树算法，它的想法是从根节点长出一棵树，然后当树枝长到终点的时候，就能从终点找到一条到根节点的唯一的路径。

基本流程：

1. 首先进行初始化，包括起点和终点的设置；
2. 进入for循环，执行Sample函数在空间中随机选择一个点Xrand；
3. Near函数寻找距离点Xrand的距离最近的节点Xnear；
4. 之后开始树的具体生长，会把Xnear和Xrand两个点连接起来作为树生长的方向，设置一个步长作为树枝的长度，然后就会产生一个新的节点Xnew，会将树枝的节点和根节点加在一起作为所有的节点；
5. 之后继续进行采样，如果两个点之间的连线会接触到障碍物，则会抛弃这次生长（这里比较有意思的判断方法是计算点和直线之间的距离，看是否大于障碍物的半径）；
6. 循环往复，直到生长到终点。（但这个概率是非常小的，所以设置一个提前停止的条件，每次产生一个Xnew节点，这个Xnew节点会和终点进行连线，然后判断之间的距离是否比步长小且中间没有障碍物，这样就可以直接连接起来）

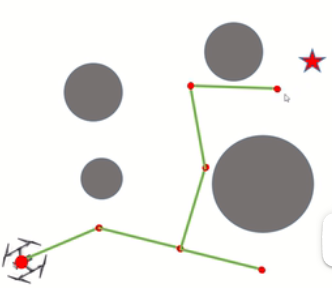
小技巧：假设我们有一定概率选择终点作为采样点的话，我们就可以直接导向终点，这样加快算法导向终点的速度。但假设终点和起点之间有障碍物的话，向终点走的过程中就会碰到障碍物而无法到达终点，所以还需要向外围进行扩展。一般设置5%-10%的概率选择终点作为采样点。

思考：这样求解出来的算法应该不是最优的吧？而且即使目标点固定不动，这个路径也是随机的，每一次生成的可能都不同。

六、RRT*算法 

正如前文中所提到的那样，RRT算法随机生成路径，并不是最优的，所以在此之上进行改进，提出RRT*算法。

在新生长树的时候还是和RRT算法一样，改进主要体现在两个方面：一是在生长完一段新的路径之后，会为新节点重新选择父节点，限定一个范围（需要之间指定），在范围内节点会作为新节点的父节点，来判断这条路径是否会更优；

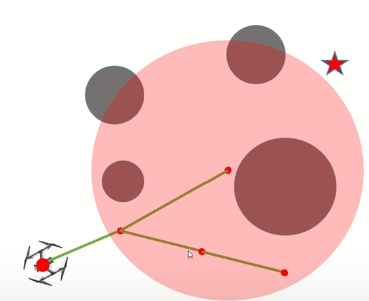
二是通过范围内的节点重新连接改进已经在树上的节点的路径。

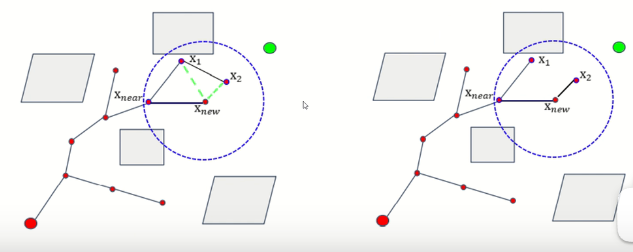
一直迭代后，最终的路径渐进最优。

 七、Informed RRT*算法 

 Informed RRT*算法提出的动机是能否增加渐进最优的速度。

限制采样的范围。找到一条路径后，采样点就会落在椭圆范围内，椭圆会越来越小，采样范围也越来越小，加快渐进最优的速度。

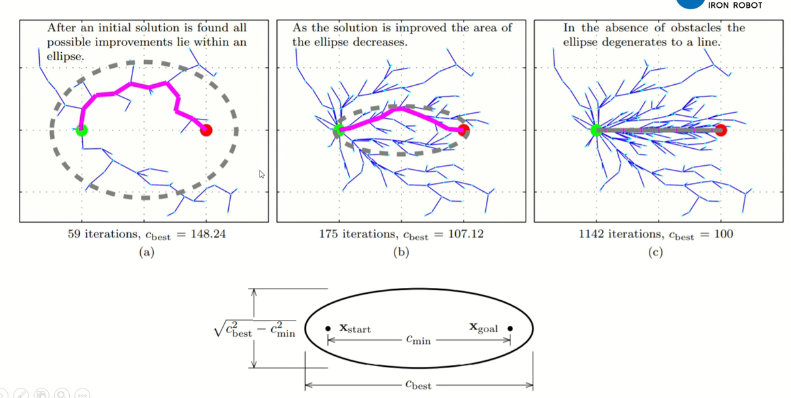
主要是在Sample函数上有所改进。先在单位圆里面采样，之后对这个单位圆进行旋转、变换和平移变成椭圆。