MATLAB | 实用(离谱)小技巧大合集：仅隐藏轴线 | 复杂公式刻度标签 | 渐变背景 | 半透明图例... ..._matlab 隐藏坐标轴

看到阿昆的科研日常写了一篇如何将轴线隐藏而不隐藏刻度的推送，使用了XRuler中的Axle对象来实现，但我试了一下R2023A版本中不太能直接用，解决了一下，同时讲一下这些有趣的隐藏对象及其其他的用法。

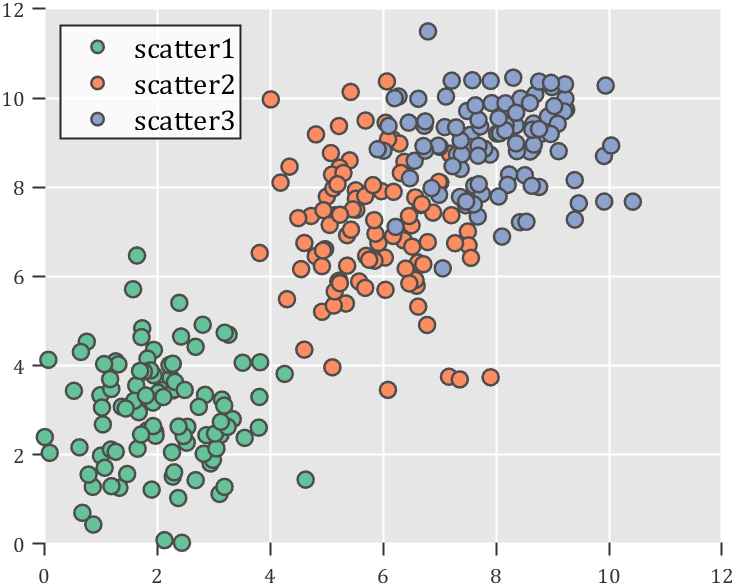
1 隐藏轴框线

假设我们编写了如下代码：

rng(12)
% 生成随机点
mu = [2 3; 6 7; 8 9];
S  = cat(3,[1 0; 0 2],[1 0; 0 2],[1 0; 0 1]);
r1 = abs(mvnrnd(mu(1,:),S(:,:,1),100));
r2 = abs(mvnrnd(mu(2,:),S(:,:,2),100));
r3 = abs(mvnrnd(mu(3,:),S(:,:,3),100));
% 绘制散点图
hold on
propCell={'LineWidth',1.2,'MarkerEdgeColor',[.3,.3,.3],'SizeData',60};
scatter(r1(:,1),r1(:,2),'filled','CData',[0.40 0.76 0.60],propCell{:});
scatter(r2(:,1),r2(:,2),'filled','CData',[0.99 0.55 0.38],propCell{:});
scatter(r3(:,1),r3(:,2),'filled','CData',[0.55 0.63 0.80],propCell{:});
% 增添图例
lgd=legend('scatter1','scatter2','scatter3');
lgd.Location='northwest';
lgd.FontSize=14;
% 半透明图例
pause(1e-6)
lgd.BoxFace.ColorType='truecoloralpha';
lgd.BoxFace.ColorData=uint8(255*[1;1;1;.8]);
% 坐标区域基础修饰
ax=gca; grid on
ax.FontName   = 'Cambria';
ax.Color      = [0.9,0.9,0.9];
ax.Box        = 'off';
ax.TickDir    = 'out';
ax.GridColor  = [1 1 1];
ax.GridAlpha  = 1;
ax.LineWidth  = 1;
ax.XColor     = [0.2,0.2,0.2];
ax.YColor     = [0.2,0.2,0.2];
ax.TickLength = [0.015 0.025];
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

在代码最后加入以下代码即可隐藏轴线：

% 隐藏轴线
ax=gca;
pause(1e-6)
ax.XRuler.Axle.LineStyle='none';
ax.YRuler.Axle.LineStyle='none';
1
2
3
4
5

注意对于比较新的版本，Axle不会直接被显示为XRuler的子对象，需要pause一下过段时间才会生成对象并被添加为XRuler的子对象，这是与老版本不同的地方。当然不设置线条格式，直接将其可见性调成否也是一种方法：

% 隐藏轴线
ax=gca;
pause(1e-6)
ax.XRuler.Axle.Visible='off';
ax.YRuler.Axle.Visible='off';
1
2
3
4
5

而如果设置线条格式，不仅仅可以设置为’none’还可以设置为’solid’ | ‘dashed’ | ‘dotted’ | ‘dashdot’ | 'none’等类型(注意观察下图x 轴)

---

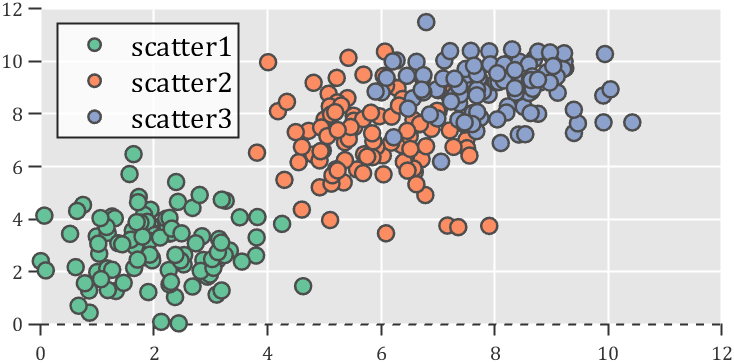
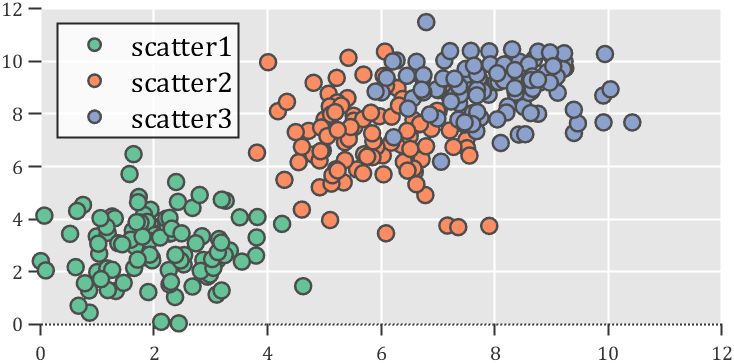
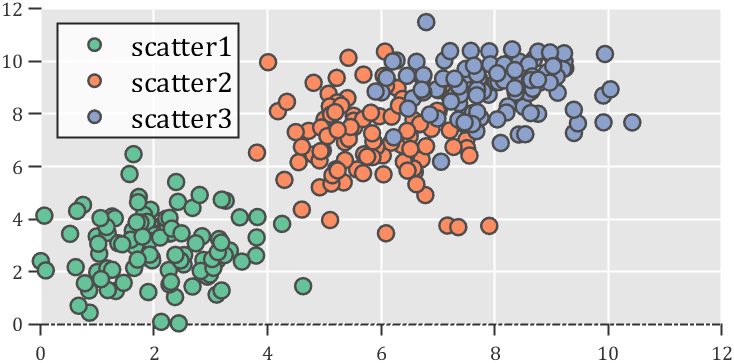
2 对数坐标轴

一般绘制对数坐标轴图可以使用下面几个函数，但是绘制出来的都是线图：

• loglog 双对数刻度图
• semilogx 半对数图（x 轴有对数刻度）
• semilogy 半对数图（y 轴有对数刻度）

怎么样其他绘图类型也使用对数刻度呢？？还是使用上面那段代码，比如我们在最后加上如下代码即可将x轴变成对数刻度(y 轴同理)：

ax=gca;
ax.XRuler.Scale='log';
1
2

有个更简单的等价方法：

ax=gca;
ax.XScale='log';
1
2

再比如填充图的对数坐标轴：

x = logspace(-1,2,1000);
y = 5 + 3*sin(x);
fill([x x(end)],[y y(1)],[0.40 0.76 0.60],'FaceAlpha',.2,...
    'LineWidth',1,'EdgeColor',[0.40 0.76 0.60])
% 坐标区域基础修饰
ax=gca; grid on;
ax.FontName  = 'Cambria';
ax.TickDir   = 'out';
ax.LineWidth = .8;
ax.Box       = 'off';
% 对数坐标轴
ax=gca;
ax.XScale='log';
1
2
3
4
5
6
7
8
9
10
11
12
13

---

3 无刻度Box框

我们box on操作后显示的框上也有刻度：

t  = linspace(pi/100,4*pi,500);
y1 = cos(t).^2;
y2 = sin(t).^2./t;
% 基础绘图
hold on
area(y1,'LineWidth',.8,'FaceColor',[0,0,.9],'FaceAlpha',.2)
area(y2,'LineWidth',.8,'FaceColor',[.8,0,0],'FaceAlpha',.2)
% 坐标区域基础修饰
ax=gca; grid on; box on
ax.FontName  = 'Cambria';
ax.TickDir   = 'out';
ax.LineWidth = 1.2;
1
2
3
4
5
6
7
8
9
10
11
12

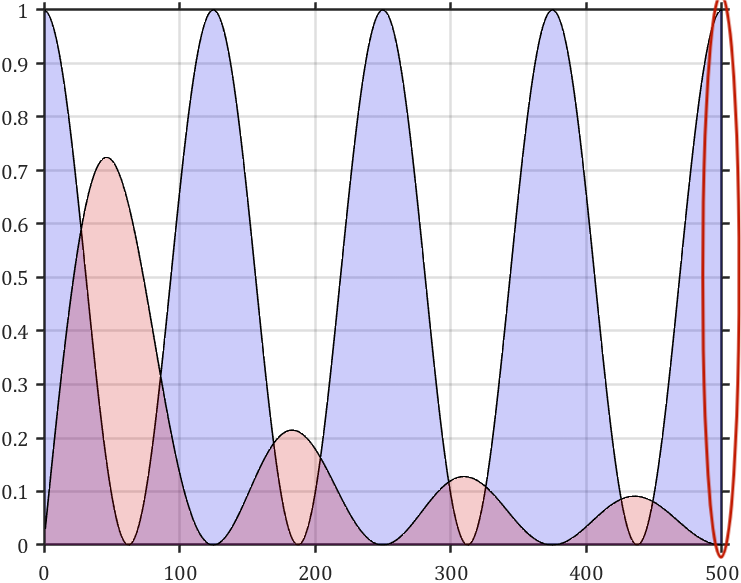
有没有啥办法不显示这个刻度呢？？虽然我们能够获取BoxFrame但这玩意并没有刻度属性，因此我们想到了直接画直线，同时为了拖动图像时直线的位置依旧在边框应该待的地方，我们为当前坐标区域增添监听，大概这样：

function testBox
t  = linspace(pi/100,4*pi,500);
y1 = cos(t).^2;
y2 = sin(t).^2./t;
% 基础绘图
hold on
area(y1,'LineWidth',.8,'FaceColor',[0,0,.9],'FaceAlpha',.2)
area(y2,'LineWidth',.8,'FaceColor',[.8,0,0],'FaceAlpha',.2)
% 坐标区域基础修饰
ax=gca; grid on; box on
ax.FontName  = 'Cambria';
ax.TickDir   = 'out';
ax.LineWidth = 1;
% 绘制可跟随移动的框线
ax=gca; box off
XLineHdl=plot(ax,ax.XLim([1,2]),ax.YLim([2,2]),'LineWidth',1,'Color',[0,0,0]);
YLineHdl=plot(ax,ax.XLim([2,2]),ax.YLim([1,2]),'LineWidth',1,'Color',[0,0,0]);
addlistener(ax,'MarkedClean',@changeLinePos)
function changeLinePos(~,~)
    set(XLineHdl,'XData',ax.XLim([1,2]),'YData',ax.YLim([2,2]))
    set(YLineHdl,'XData',ax.XLim([2,2]),'YData',ax.YLim([1,2]))
end
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

当然我们这么用不咋方便，我们可以将其封装为函数：

function addBox
ax=gca; box off
XLineHdl=plot(ax,ax.XLim([1,2]),ax.YLim([2,2]),'LineWidth',ax.LineWidth,'Color',ax.XColor);
YLineHdl=plot(ax,ax.XLim([2,2]),ax.YLim([1,2]),'LineWidth',ax.LineWidth,'Color',ax.YColor);
addlistener(ax,'MarkedClean',@changeLinePos)
function changeLinePos(~,~)
    set(XLineHdl,'XData',ax.XLim([1,2]),'YData',ax.YLim([2,2]))
    set(YLineHdl,'XData',ax.XLim([2,2]),'YData',ax.YLim([1,2]))
end
end
1
2
3
4
5
6
7
8
9
10

这样画完图之后在最后加一行addBox()即可，框的颜色及粗细会和轴的颜色相图：

t  = linspace(pi/100,4*pi,500);
y1 = cos(t).^2;
y2 = sin(t).^2./t;
% 基础绘图
hold on
area(y1,'LineWidth',.8,'FaceColor',[0,0,.9],'FaceAlpha',.2)
area(y2,'LineWidth',.8,'FaceColor',[.8,0,0],'FaceAlpha',.2)
% 坐标区域基础修饰
ax=gca; grid on; box on
ax.FontName  = 'Cambria';
ax.TickDir   = 'out';
ax.LineWidth = 1;
ax.XColor    = [0,0,.8];
ax.YColor    = [.8,0,0];

addBox()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

---

4 三维框的颜色

假设我们编写了如下代码：

% 获取数据
X1=normrnd(2,2,1,50);
X2=[normrnd(4,4,1,50),normrnd(5,2,1,50)];
X3=[normrnd(6,2,1,50),normrnd(8,4,1,50)];
X4=[normrnd(12,1,1,50),normrnd(12,4,1,50)];
X5=[normrnd(10,2,1,50),normrnd(10,4,1,50)];
X6=[normrnd(7,2,1,50),normrnd(7,4,1,50)];
X7=[normrnd(4,2,1,50),normrnd(4,4,1,50)];
Data={X1,X2,X3,X4,X5,X6,X7};
Y=zeros(7,500);
for i=1:length(Data)
    tX=Data{i};tX=tX(:)';
    [F,Xi]=ksdensity(tX,linspace(-5,10,500));
    Y(i,:)=F;
end
X=Xi;

YLim=[min(min(Y)),max(max(Y))];
% 构造并绘制网格
[XMesh,YMesh]=meshgrid(X,linspace(YLim(1),YLim(2),1000));
hold on
for i=1:size(Y,1)
    YMeshA=repmat(Y(i,:),[1000,1]);
    CMesh=nan.*XMesh;
    YMeshD=YMeshA-YLim(1);
    CMesh(YMesh>=YLim(1)&YMesh<=YMeshA)=YMeshD(YMesh>=YLim(1)&YMesh<=YMeshA);
    surf(XMesh,XMesh.*0+i,YMesh,'EdgeColor','none','CData',CMesh,'FaceColor','flat','FaceAlpha',.8)
end

% 绘制折线图
for i=1:size(Y,1)
    plot3(X,X.*0+i,Y(i,:),'LineWidth',1,'Color',[0,0,0,.8])
end

% 设置配色
colorList=turbo(64);
% colorList=slanCM(110,64);
colormap(colorList)
colorbar

% 坐标区域修饰
ax=gca;hold on;box on
ax.XGrid='on';
ax.YGrid='on';
ax.XMinorTick='on';
ax.YMinorTick='on';
ax.LineWidth=.8;
ax.GridLineStyle='-.';
ax.FontName='Cambria';
ax.FontSize=12;
ax.GridAlpha=.03;
ax.Projection='perspective';
ax.GridAlpha=.05;
ax.BoxStyle='full';
view(16,36)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

可以通过boxFrame属性设置每个框线的颜色：

% 设置框线颜色
ax=gca;
pause(1e-6);
ax.BoxFrame.XColor=[1,0,0];
ax.BoxFrame.YColor=[0,1,0];
ax.BoxFrame.ZColor=[0,0,1];
1
2
3
4
5
6

可以看到仅仅框线变色，轴线不变色，此属性仅仅为显示属性，保存时无法保留颜色，因此建议绘制折线硬画：

---

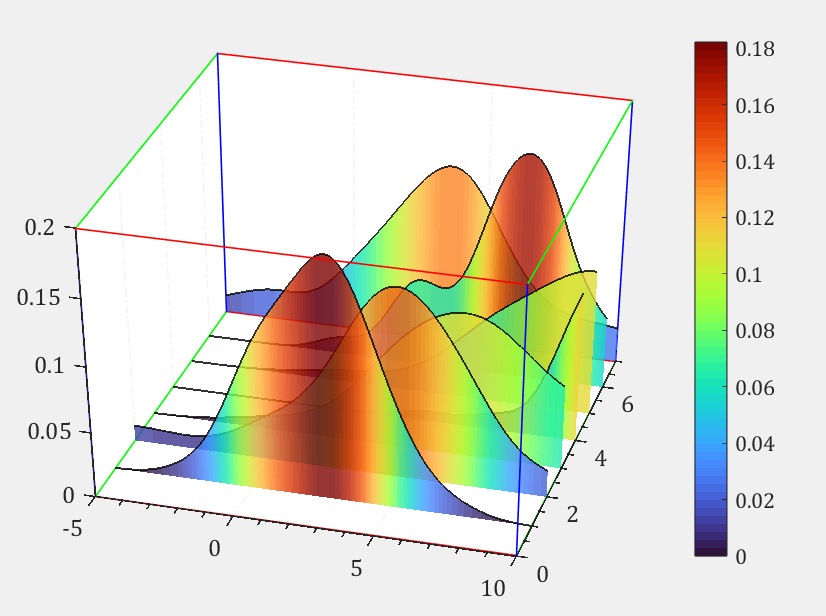
把之前写的一小部分东西拿过来再提一下：

5 更改3D图轴位置

对于hAxes=gca

• hAxes.XRuler.FirstCrossoverValue
  X轴在Y轴上的位置
• hAxes.XRuler.SecondCrossoverValue
  X轴在Z轴上的位置
• hAxes.YRuler.FirstCrossoverValue
  Y轴在X轴上的位置
• hAxes.YRuler.SecondCrossoverValue
  Y轴在Z轴上的位置
• hAxes.ZRuler.FirstCrossoverValue
  Z轴在X轴上的位置
• hAxes.ZRuler.SecondCrossoverValue
  Z轴在Y轴上的位置

一个实例：

N = 49;
X = linspace(-10,10,N);
Z = peaks(N);
mesh(X,X,Z);

hAxes=gca;
hAxes.LineWidth=1.5;
hAxes.XRuler.FirstCrossoverValue  = 0; % X轴在Y轴上的位置 
hAxes.YRuler.FirstCrossoverValue  = 0; % Y轴在X轴上的位置 
hAxes.ZRuler.FirstCrossoverValue  = 0; % Z轴在X轴上的位置 
hAxes.ZRuler.SecondCrossoverValue = 0; % Z轴在Y轴上的位置 
1
2
3
4
5
6
7
8
9
10
11

---

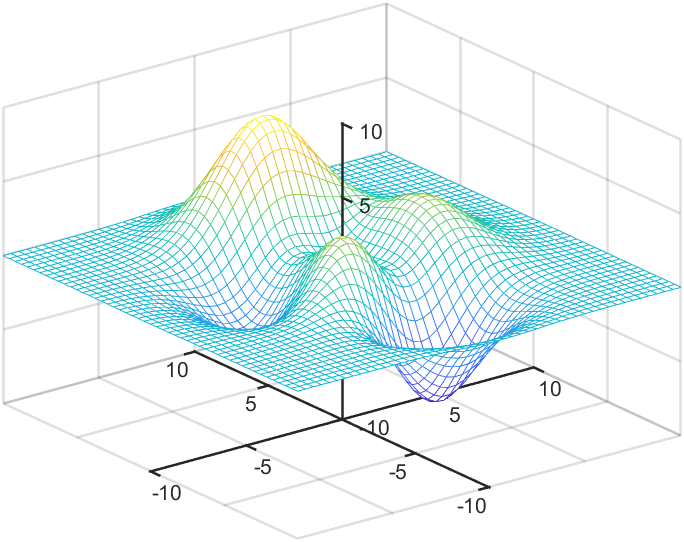
6 修改坐标区域背景

我们知道可以通过设置

set(gca,'Color',[1,0,0])
1

类似的形式设置背景颜色，但这只是纯色，那么有啥办法把背景色换成渐变色？

t=0.2:0.01:3*pi;

hold on
plot(t,cos(t)./(1+t),'LineWidth',4)
plot(t,sin(t)./(1+t),'LineWidth',4)
plot(t,cos(t+pi/2)./(1+t+pi/2),'LineWidth',4)
plot(t,cos(t+pi)./(1+t+pi),'LineWidth',4)
legend


ax=gca;pause(1e-16);% Backdrop建立需要一定时间因此pause一下很重要
% 四列分别为四个角的颜色
% 使用4xN大小颜色矩阵
% 四行分别是R,G,B,和透明度
colorData = uint8([255, 150, 200, 100; ... 
                   255, 100,  50, 200; ...
                     0,  50, 100, 150; ...
                   102, 150, 200,  50]);
set(ax.Backdrop.Face, 'ColorBinding','interpolated','ColorData',colorData);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

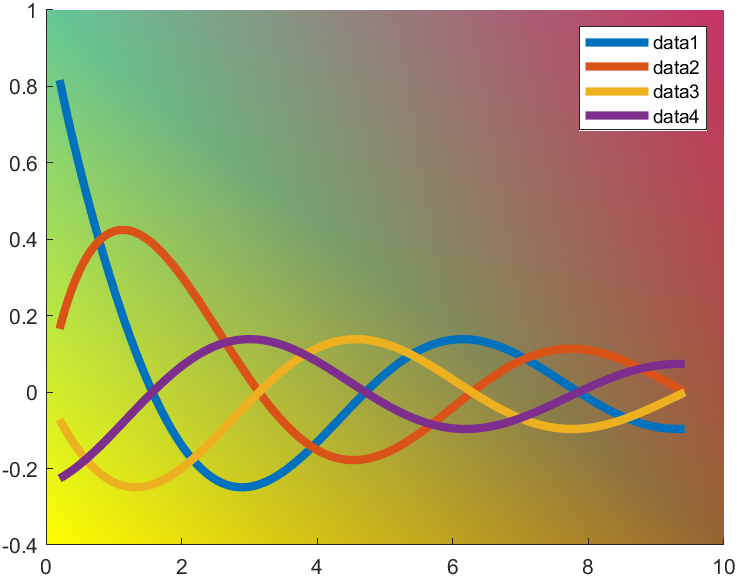
7 半透明及渐变图例

t=0.2:0.01:3*pi;

hold on
plot(t,cos(t)./(1+t),'LineWidth',4)
plot(t,sin(t)./(1+t),'LineWidth',4)
plot(t,cos(t+pi/2)./(1+t+pi/2),'LineWidth',4)
plot(t,cos(t+pi)./(1+t+pi),'LineWidth',4)
hLegend=legend();
% 设置图例为半透明
pause(1e-16)
set(hLegend.BoxFace,'ColorType','truecoloralpha','ColorData',uint8(255*[1;1;1;.5])); 

set(gca,'Color',[0,0,.18]);
1
2
3
4
5
6
7
8
9
10
11
12
13

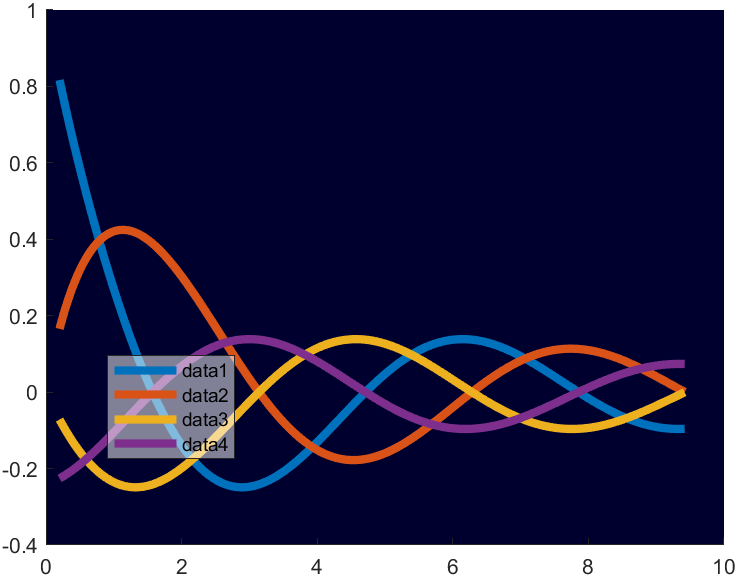
当然也可以花里胡哨：

t=0.2:0.01:3*pi;
hold on
plot(t,cos(t)./(1+t),'LineWidth',4)
plot(t,sin(t)./(1+t),'LineWidth',4)
plot(t,cos(t+pi/2)./(1+t+pi/2),'LineWidth',4)
plot(t,cos(t+pi)./(1+t+pi),'LineWidth',4)
hLegend=legend();

% 设置图例为渐变色
pause(1e-16)
colorData = uint8([255, 150, 200, 100; ... 
                   255, 100,  50, 200; ...
                     0,  50, 100, 150; ...
                   102, 150, 200,  50]);
set(hLegend.BoxFace,'ColorBinding','interpolated','ColorData',colorData)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

---

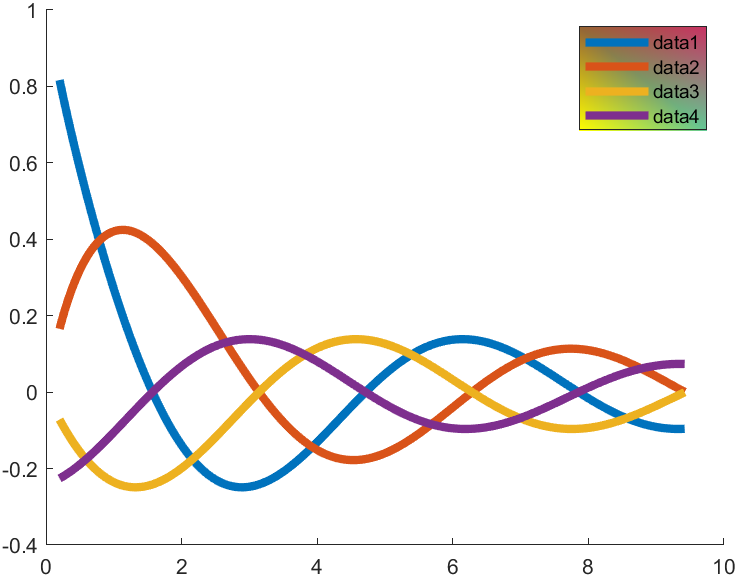
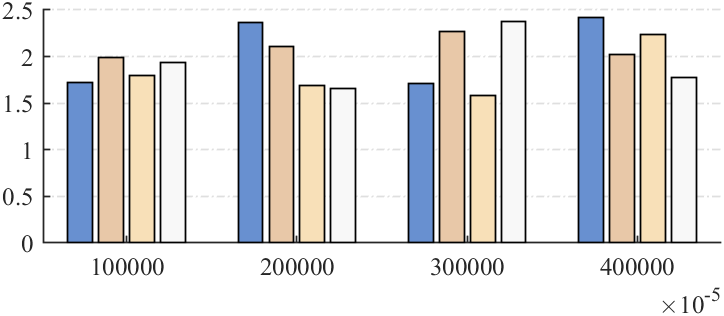
8 轴标签的科学计数法

我们想将刻度值用科学计数法表示咋办，假如编写了如下代码：

rng(5)
% 随机生成数据
X=1.5+rand(4,4);
% 基础绘图
ax=gca;hold on;
bHdl=bar(X,'LineWidth',.8);
% 修改配色
CList=[0.4078    0.5647    0.8157
    0.9098    0.7843    0.6588
    0.9725    0.8784    0.7216
    0.9725    0.9725    0.9725];
bHdl(1).FaceColor=CList(1,:);
bHdl(2).FaceColor=CList(2,:);
bHdl(3).FaceColor=CList(3,:);
bHdl(4).FaceColor=CList(4,:);
% 坐标区域修饰
ax.FontName='Times New Roman';
ax.LineWidth=.8;
ax.FontSize=12;
ax.YGrid='on';
ax.GridLineStyle='-.';
ax.XTick=1:4;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

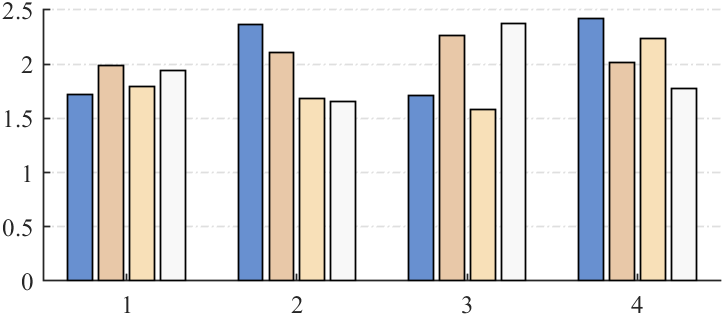
在最后编写如下代码使用科学计数法：

ax=gca;
ax.XRuler.Exponent=-5;
1
2

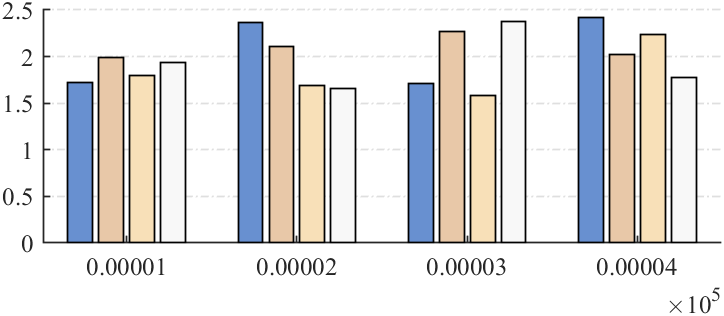
ax=gca;
ax.XRuler.Exponent=5;
1
2

---

9 更复杂的标签公式

刻度标签也可以改成支持latex，还是上面的绘图函数，在最后加上：

ax.XRuler.TickLabelInterpreter='latex';
ax.XTickLabel={'$\Delta A B C$','$\frac{n!}{r!(n-r)!} $','$\left(\begin{array}{cc}A& B\\C& D\end{array}\right)$','$E = n{{ \Delta \Phi } \over {\Delta {t} }}  $'}
1
2

---

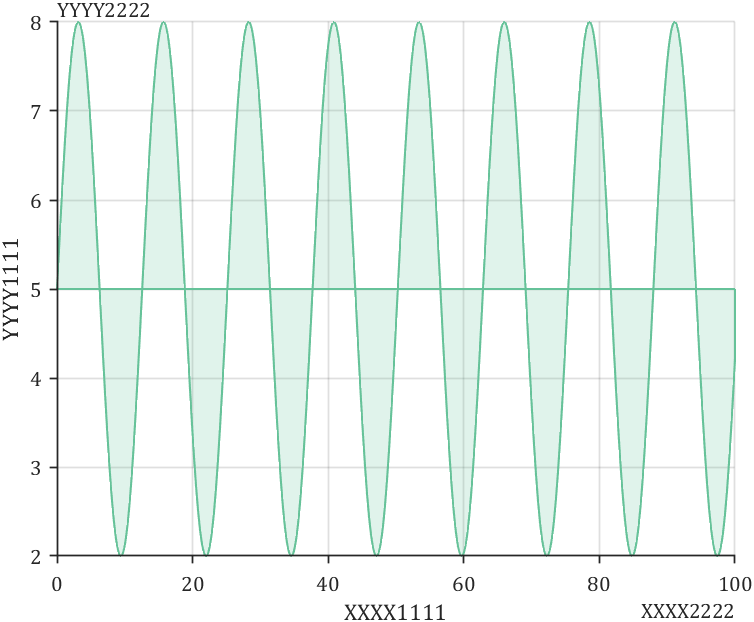
10 显示次标签

最后讲一下如何显示X轴及Y轴次标签：

x = linspace(0,100,1000);
y = 5 + 3*sin(x./2);
fill([x x(end)],[y y(1)],[0.40 0.76 0.60],'FaceAlpha',.2,...
    'LineWidth',1,'EdgeColor',[0.40 0.76 0.60])
% 坐标区域基础修饰
ax=gca; grid on;
ax.FontName  = 'Cambria';
ax.TickDir   = 'out';
ax.LineWidth = .8;
ax.Box       = 'off';

% 显示次标签
ax=gca;
% X轴主次标签
xlabel('XXXX1111')
ax.XRuler.SecondaryLabel.String='XXXX2222';
ax.XRuler.SecondaryLabel.Visible='on';
% Y轴主次标签
ylabel('YYYY1111')
ax.YRuler.SecondaryLabel.String='YYYY2222';
ax.YRuler.SecondaryLabel.Visible='on';
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

---

完

本期已经足够长了，等有下期可能会补充其他的MATLAB中的离谱操作！！！