C语言与密码学算法实现：RSA、AES、ECC等公钥与对称加密算法详解（二）_rsa模密运算c语言

目录

一、RSA公钥加密算法详解与C语言实现

RSA原理

密钥生成过程

RSA加密与解密流程

二、AES对称加密算法详解与C语言实现

AES原理

密钥扩展过程

加密/解密的多轮操作

AES优缺点与适用场景

---

一、RSA公钥加密算法详解与C语言实现

RSA原理

RSA算法基于数论中的几个核心概念，主要包括欧拉函数、欧拉定理、以及模逆运算。

欧拉函数（Euler's totient function）记为φ(n)，表示小于n且与n互素（即最大公约数为1）的正整数个数。对于两个大素数p和q的乘积n = pq，欧拉函数φ(n)可简化为φ(n) = (p-1)(q-1)。

欧拉定理指出，若a与n互素，则a的φ(n)次方与1模n同余，即a^(φ(n)) ≡ 1 (mod n)。

模逆运算是指在整数模运算中寻找一个数b的逆元c，使得a*b ≡ 1 (mod n)。对于RSA而言，就是找到满足ed ≡ 1 (mod φ(n))的整数d，即d为e关于φ(n)的模逆。

密钥生成过程

RSA密钥生成步骤如下：

1. 选择两个大素数 p 和 q。通常选取的素数足够大以保证安全性，如接近512位或更长。

2. 计算乘积 n = p*q。n是公钥和私钥共有的部分，公开给所有通信方。

3. 计算欧拉函数 φ(n) = (p-1)*(q-1)。φ(n)用于后续确定公钥和私钥的指数关系。

4. 选择公钥指数 e。e是一个与φ(n)互素的整数，且满足1 < e < φ(n)。通常e取一个较小的素数（如65537），以提高计算效率。

5. 计算私钥指数 d。使用扩展欧几里得算法或其他模逆计算方法找到d，使得d * e ≡ 1 (mod φ(n))。d是私钥的一部分，必须保密。

最终，公钥为(e, n)，私钥为(d, n)。

RSA加密与解密流程

RSA加密过程： 给定明文m和公钥(e, n)，加密过程通过幂模运算完成：

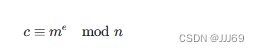
其中，c为加密后的密文。

RSA解密过程： 持有私钥(d, n)的接收者对密文c进行解密：

通过幂模运算，原始明文m得以恢复。

C语言实现RSA算法

由于篇幅限制，这里仅概述关键函数与数据结构设计，而不直接提供完整的源代码片段。实际实现时，通常需要借助大整数库来处理超过常规整数类型的数值。

关键函数与数据结构：

• 密钥生成函数：实现上述密钥生成过程，包括素数检测、乘积计算、欧拉函数计算、公钥指数选择、模逆计算，最后封装公钥和私钥。

• 加密函数：接受明文m、公钥(e, n)，执行幂模运算，返回密文c。

• 解密函数：接受密文c、私钥(d, n)，执行幂模运算，返回明文m。

编程挑战与解决方案：

• 大整数运算：标准C语言并不直接支持大整数运算。开发者需要自行实现或使用第三方库进行大数加减乘除、幂运算以及模运算。实现时需要注意数据结构设计（如数组、链表、或专门的大整数类）、溢出处理、运算效率优化等。

• 模逆计算：求解模逆是一个相对复杂的数学问题。常用的方法包括扩展欧几里得算法、快速傅里叶变换（FFT）加速的中国剩余定理（CRT）等。确保算法正确性和高效性至关重要，特别是对于大素数情况下φ(n)的计算。

总结来说，RSA公钥加密算法基于坚实的数论基础，通过精心设计的密钥生成过程确保了安全性。C语言实现时，需重点解决大整数运算和模逆计算的难题，可以借助成熟的库或算法来提高实现效率和准确性。实际应用中，RSA常与其他加密算法结合使用，以平衡安全性与计算效率。

二、AES对称加密算法详解与C语言实现

AES（Advanced Encryption Standard，高级加密标准）是一种广泛使用的对称密钥加密算法，以其高效性、安全性、标准化程度高等优点，在众多信息安全领域中占据重要地位。本节将详细介绍AES的基本结构、密钥扩展过程以及加密/解密的多轮操作，并探讨其优缺点及典型应用场景。

AES原理

基本结构

AES采用分组密码体制，其核心结构包括迭代模式、轮函数、以及四个基本操作：SubBytes、ShiftRows、MixColumns、AddRoundKey。

迭代模式：AES对明文数据按128位（16字节）分组进行处理。对于更长的明文，通常使用CBC（Cipher Block Chaining）、CFB（Cipher Feedback）、OFB（Output Feedback）或CTR（Counter）等模式实现分组间的链接，确保整体加密的保密性和完整性。

轮函数：AES加密过程包括若干轮（取决于密钥长度：10轮 for AES-128，12轮 for AES-192，14轮 for AES-256）的重复计算。每一轮由以下四个基本操作组成：

1. SubBytes：将每个分组中的每个字节替换为S盒（S-Box）中对应的字节，实现非线性变换，增强了抵抗代数攻击的能力。S盒的设计基于复杂的数学运算，确保了良好的扩散性和混淆性。

2. ShiftRows：将分组内的字节行进行循环移位，使得每一行中的元素与其在其他行的对应元素错开，增加了数据的相关性，进一步扩散了输入变化的影响。

3. MixColumns：对分组内的每一列（四个字节视为一个四元多项式）应用固定的线性混合操作，实现跨列的扩散。此操作增强了密码强度，即使输入的微小变化也会在输出中产生显著差异。

4. AddRoundKey：将当前轮密钥与分组进行异或操作（XOR），将密钥信息直接融入加密过程中。每一轮的密钥不同，由初始密钥经过密钥扩展算法生成。

密钥扩展过程

初始密钥（长度为128、192或256位）经过密钥扩展算法生成一系列子密钥（round keys），每个子密钥用于对应的一轮加密或解密操作。密钥扩展过程涉及轮密钥的复制、循环移位和异或操作，确保生成的子密钥之间具有足够的独立性和相关性。

加密/解密的多轮操作

• 加密：首先，明文分组与初始轮密钥进行AddRoundKey操作。接着进行多次（根据密钥长度确定轮数）的轮函数计算，每轮包括SubBytes、ShiftRows、MixColumns和AddRoundKey。最后一轮省略MixColumns操作，以保持加密的扩散度和混淆度平衡。最后，再次执行AddRoundKey，使用最后一个子密钥完成加密过程。

• 解密：解密过程与加密过程类似，但轮函数的操作顺序反转且使用对应的逆操作。具体而言，先进行AddRoundKey（使用最后一个子密钥），然后进行多轮解密轮函数，包括InvSubBytes（SubBytes的逆操作）、InvShiftRows（ShiftRows的逆操作）、InvMixColumns（MixColumns的逆操作），并在最后一轮省略InvMixColumns。最后，使用初始密钥进行最后一次AddRoundKey，恢复明文。

AES优缺点与适用场景

优点：

• 安全性：AES经过严格的安全性评估，目前未发现有效的已知攻击，能够在合理的时间内保证数据的安全。
• 效率：AES设计时考虑了硬件和软件的高效实现，无论是基于专用硬件加速器还是通用处理器，都能达到较高的加密速度。
• 标准化程度：AES已被国际标准化组织（ISO）、国际电工委员会（IEC）、美国国家标准与技术研究院（NIST）等多个权威机构采纳为标准，全球范围内得到广泛应用。
• 灵活性：支持多种分组模式和不同的密钥长度，可根据实际应用需求选择合适的配置。

局限性：

• 密钥管理：对称加密算法的共同挑战在于密钥的分发与安全管理。由于加密和解密使用同一密钥，双方必须事先共享密钥且保证密钥在整个生命周期中的保密性，这在大规模分布式环境中可能较为复杂。
• 数据完整性保护：AES本身仅提供保密性，不直接提供数据完整性保护。通常需要结合消息认证码（MAC）或使用基于AES的 authenticated encryption modes（如GCM、CCM）来确保数据完整性和抗重放攻击。

典型应用场景：

• 文件加密：AES可用于保护存储在硬盘、移动设备或云存储中的敏感文件，确保数据在静止状态下的保密性。
• 网络通信：在SSL/TLS协议、IPsec VPN、WPA/WPA2 Wi-Fi安全等网络通信场景中，AES用于加密传输的数据，保障通信内容的私密性。
• 数据库加密：在存储敏感个人信息或企业数据的数据库系统中，AES可用于加密存储的数据项，增强数据在存储层面的安全防护。
• 硬件加密模块：许多智能卡、嵌入式设备和安全芯片内置AES引擎，用于快速、安全地处理加密操作。

综上所述，AES作为现代密码学中的核心加密算法，凭借其优越的安全性、高效性和标准化特性，广泛应用于各类信息安全场景中，有效保护数据免受未经授权的访问。尽管在密钥管理方面存在挑战，但通过合理的密钥生命周期管理和安全协议设计，可以有效克服这一局限性。