【DBO三维路径规划】蜣螂优化算法DBO复杂山地环境下无人机三维路径规划【含Matlab源码 3574期】_dbo优化算法 路径规划优点

⛄一、蜣螂算法无人机避障三维航迹规划简介

1 无人机航迹规划问题的数学模型
建立三维航迹规划问题的数学模型时, 不但考虑无人机基本约束, 还考虑复杂的飞行环境, 包括山体地形和雷暴威胁区。

1.1 无人机基本约束
规划的无人机三维航迹, 通常需要满足一些基本约束, 包括最大转弯角、最大爬升角或下滑角、最小航迹段长度、最低和最高飞行高度, 以及最大航迹长度等约束。其中, 最大转弯角约束, 是指无人机只能在水平面内小于或等于指定的最大转弯角内转弯;最大爬升角或下滑角约束, 是指无人机只能在垂直平面内小于或等于指定的最大爬升角或下滑角内爬升或下滑;最小航迹段长度约束, 要求无人机改变飞行姿态之前, 按目前的航迹方向飞行的最短航程;最低和最高飞行高度约束, 要求无人机在指定的飞行高度区间飞行;最大航迹长度约束, 是指无人机的航迹长度小于或等于指定的阈值。

记q (x, y, z, θ, ψ) 为无人机的飞行位置与姿态, 其中, (x, y, z) 为无人机的位置, θ为无人机的水平转弯角, ψ为无人机的竖直爬升角或下滑角, 进而建立上述基本约束的数学表达式。

1.2 飞行环境障碍物和威胁区建模
在飞行环境中, 高耸的山体近似采用圆锥体等效表示, 用以e为底的自然指数图形生成, 那么, 山体地形可以通过多个位置不同的圆锥体叠加而成。若将参考海拔基准高度设置为xOy平面, 记 (x, y, z) 为山体地形中的点, 那么

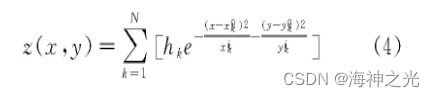
式中:N为山体个数;xk0和yk0为第k座山体中心对称轴的横坐标和纵坐标;hk为第k座山体的最大高度;xki和yki为第k座山体的横向斜度和纵向斜度。

在飞行环境中, 山体附近通常存在雷暴等极端气象, 本文视为飞行威胁区, 并通过球体近似等效表示, 且记第k座山体附近飞行威胁区的球心坐标为 (xks0, yks0, zks0) , 半径为rk。

1.3 目标函数及航迹表示
在本文中, 执行任务的某型无人机, 其航迹规划的目标函数是生成一条由起始点到目标点的无碰撞可行航迹。采用q (x, y, z, θ, ψ) 表示无人机在飞行空域中某特定位置的特定姿态, 那么 (x, y, z) 则表示无人机所在航迹点, θ表示无人机的水平转弯角, ψ表示无人机的竖直爬升角或下滑角。采用r (q) 表示由起始点qinitial到目标点qgoal的无碰撞可行航迹, 那么航迹规划的过程可以写成如下形式:

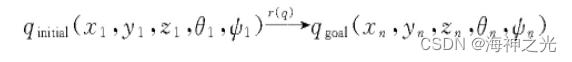
2 蜣螂算法
摘要：蜣螂优化算法( Dung beetle optimizer, DBO), 是由 Jiankai Xue 等于2022 年提出的一种群体智能优化算法。其灵感来源于蜣螂的生物行为过程，具有寻优能力强，收敛速度快的特点。
1 蜣螂优化算法
众所周知，蜣螂是自然界中一种常见的昆虫，动物的粪便为食，在全世界内分布广泛，扮演着自然界中分解者的角色，对生态系统平衡起着至关重要的作用。蜣螂有一个有趣的习惯，它们会把粪便捏成球，然后把它滚出来，目的是能够尽可能快速、有效地移动粪球，防止被其他蜣螂抢夺。蜣螂的可以利用天体线索(特别是太阳、月亮和偏振光)来导航，让粪球沿着直线滚动，如果完全没有光源(也就是在完全黑暗的环境中)，蜣螂的就不再走直线，而是弯曲的，有时甚至略圆，有很多因素(如风、地面不平)都会导致蜣螂偏离原来的方向，蜣螂在滚粪球的过程如遇到障碍物而无法前进时，通常会爬到粪球上面"跳舞"(包括一系列的旋转和停顿)，决定它们的运动方向。

从蜣螂的习性中观察发现，其获取粪球主要有以下两个目的：①用来产卵和养育下一代；②作为食物。蜣螂会把粪球埋起来，雌性蜣螂会在粪球里产卵，粪球不仅是蜣螂幼虫的发育场所，也是必需的食物。所以，粪球对蜣螂的生存起着不可替代的作用。

本位介绍了一种新的群体智能优化算法------DBO（Dung beetle optimizer）技术，其灵感主要来源于蜣螂的滚球、跳舞、觅食、偷窃、和繁殖等行为。

1.1 结构和算法
根据上面的讨论，蜣螂在滚动过程中需要通过天体线索导航，以保持粪球在直线路径上滚动。为了模拟滚球行为，要求蜣螂在整个搜索空间中沿着给定的方向移动。蜣螂的运动轨迹如图1所示。在图1中，蜣螂利用太阳来导航，其中红色箭头表示的是滚动的方向,同时，我们假设光源的强度也会影响蜣螂的路径。

1.2 计算步骤
DBO 算法作为一种新颖的基于 SI 的优化技术, 主要有六个步骤:
(1) 初始化蜣螂群和 DBO 算法的参数;
(2) 根据目标函数计算出所有目标代理的适应度值;
(3) 更新所有蛲螂的位置;
(4) 判断每个目标代理是否超出边界;
(5) 更新当前最优解及其适应度值;
(6) 重复上述步骤, 直到 t 满足终止准则, 输出全局最优解及其适应度值。

⛄二、部分源代码

close all
clear
clc
addpath(‘./Algorithm/’)%添加算法路径
warning off;
%% 三维路径规划模型定义
global startPos goalPos N
N=2;%待优化点的个数(可以修改)
startPos = [10, 10, 80]; %起点(可以修改)
goalPos = [80, 90, 150]; %终点(可以修改)
SearchAgents_no=30; % 种群大小(可以修改)
Function_name=‘F2’; %F1:随机产生地图 F2：导入固定地图
Max_iteration=100; %最大迭代次数(可以修改)
% Load details of the selected benchmark function
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
[Best_score,Best_pos,curve]=DBO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);%算法优化求解
AlgorithmName=‘DBO’;%算法名字
figure
plot(curve,‘Color’,‘r’,‘linewidth’,2)
xlabel(‘迭代次数’);
ylabel(‘飞行路径长度’);
legend(AlgorithmName)
display(['算法得到的最优适应度: ‘, num2str(Best_score)]);
Position=[Best_pos(1:dim/3); Best_pos(1+dim/3:2*(dim/3)); Best_pos(1+(2*dim/3):end)]’; %优化点的XYZ坐标（每一行是一个点）
plotFigure(Best_pos,AlgorithmName)%画最优路径

⛄三、运行结果

⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]田疆,李二超.用于无人机三维航迹规划改进连接型快速扩展随机树算法[J].航空工程进展. 2018,9(04)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除