- 1浅谈深度学习
- 2齐治堡垒机任意用户登录漏洞_/audit/gui_detail_view.php
- 3【Sql Server】Update中的From语句,以及常见更新操作方式_sql update from
- 4python php web 大流量_PHP解决网站大数据大流量与高并发
- 5DevEco组件(笔记)_deveco studio text组件
- 6SQL与Oracle对比 _rownum<=20000 and rownum>=10000
- 7国产Heygen!阿里EMO,照片+音频,生成人像视频_阿里 emo
- 8客户端会话跟踪技术 Cookie 浅谈_追踪cookie
- 9Anaconda的安装以及使用清华源镜像安装pytorch_anaconda3-5.3.1-windows-x86_64.exe
- 10python 栅格数据裁剪_矢量裁剪栅格python
密码分析(一):差分密码分析
赞
踩
差分分析是一种选择明文攻击,其基本思想是:通过分析特定明文差分对相对应密文差分影响来获得尽可能大的密钥。它可以用来攻击任何由迭代一个固定的轮函数的结构的密码以及很多分组密码(包括DES),它是由Biham和Shamir于1991年提出的选择明文攻击。
一、选择明文攻击(chosen-plaintext attack, CPA)
通过选择对攻击有利的特定明文及对应的密文,求解密钥或从截获的密文求解相应明文的密码分析方法。
在选择明文攻击时,密码分析者对明文有选择或控制的能力,可选择他认为有利于攻击的任何明文及其对应的密文,是一种比已知明文攻击更强的攻击方式。如果一个密码系统能够抵抗选择明文攻击,那么必然能够抵抗唯密文攻击和已知明文攻击。
选择明文攻击较难实现。一种情形是假设密码分析者临时获得加密机器的访问权,但加密密钥被安全嵌入在设备中,分析者得不到密钥,此时可通过加密大量选择的明文,然后利用产生的密文来推测密钥。
已知:
P
1
,
C
1
=
E
k
(
P
1
)
,
P
2
,
C
2
=
E
k
(
P
2
)
,
.
.
.
,
P
i
,
C
i
=
E
k
(
P
i
)
P_1,C_1=E_k(P_1),P_2,C_2=E_k(P_2),...,P_i,C_i=E_k(P_i)
P1,C1=Ek(P1),P2,C2=Ek(P2),...,Pi,Ci=Ek(Pi),其中,
P
1
,
P
2
,
.
.
.
,
P
i
P_1,P_2,...,P_i
P1,P2,...,Pi可由密码分析者选择。
推导出:密钥K,或从
C
i
+
1
=
E
k
(
P
i
+
1
)
C_{i+1}=E_k(P_{i+1})
Ci+1=Ek(Pi+1) 推导出
P
i
+
1
P_{i+1}
Pi+1的算法。
典型的选择明文攻击方法有碰撞攻击和差分攻击等。本篇主要讲解差分攻击的原理,过程以及实例。
二、差分密码分析(differential cryptanalysis)
1.原理
差分分析的目标是获得加密的子密钥。
差分分析最早由Murphy于1990年提出,随后 Biham 和 Shamir 又在一系列研究里对该技术进行了发展,适用于过度使用异或操作的分组密码算法。
所谓差分分析,是指追踪明文对的“差异”的传播。这里的“差异”由我们根据目标进行定义,可以是异或值,也可以是其它。针对DES,使用的就是异或值定义“差异”,或者称之为“距离”,有些地方也称为“特征”(characteristic)。
比如说,选定明文
P
1
P_1
P1,明文之间的“差值”(differential)为
δ
\delta
δ,于是另一个明文就是
P
1
+
δ
P_1+\delta
P1+δ,明文
P
1
P_1
P1对应的密文为
C
1
C_1
C1,明文
P
1
+
δ
P_1+\delta
P1+δ对应的密文与
C
1
C_1
C1的“距离”是
ε
\varepsilon
ε
P
1
→
C
1
P
1
+
δ
→
C
1
+
ε
P_1 \rarr C_1 \newline P_1+\delta \rarr C_1+\varepsilon
P1→C1P1+δ→C1+ε
如果
δ
\delta
δ 以一定的概率对应着
ε
\varepsilon
ε,就称
δ
\delta
δ 是一个差分特征。其实这个过程主要关注的是非线性函数,AES中主要是S盒非线性,DES是Feistel结构中的F函数。
2.过程
一般的S盒是以2进制进行表示的,即 π s : { 0 , 1 } m → π s : { 0 , 1 } n \pi_s:{\{0,1\}}^m \rarr \pi_s:{\{0,1\}}^n πs:{0,1}m→πs:{0,1}n是一个S盒,对二进制的S盒的攻击很多文献都有给出,也可参考《密码学原理与实践(第三版)》3.4 差分密码分析。本文以下面10进制内的S盒为例,讲解差分攻击的主要过程。
| x x x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| S [ x ] S[x] S[x] | 2 | 6 | 8 | 7 | 1 | 4 | 9 | 5 | 3 | 0 |
2.1 S盒差分分布表
来学嘉等人在文献1 中给出了一般意义下的差分概念,即对群
(
G
,
⋅
)
(G,\cdot)
(G,⋅)中的两个元素
X
,
X
∗
X,X^*
X,X∗,
X
X
X和
X
∗
X^*
X∗的差分定义为
Δ
X
=
X
⋅
(
X
∗
)
−
1
\Delta X = X \cdot (X^*)^{-1}
ΔX=X⋅(X∗)−1。
Granboulan等人2 研究提出了当分组不是比特串时的通用框架,就像我们使用的是十进制数。使用一个
q
×
q
q \times q
q×q的矩阵
Δ
\Delta
Δ模拟S盒的差异,
Δ
\Delta
Δ定义如下:
Δ
(
S
)
a
,
a
′
=
#
{
x
∣
S
(
x
+
α
)
−
S
(
x
)
=
β
}
\Delta(S)_{a,a'} =\# \{x|S(x+\alpha)-S(x) = \beta\}
Δ(S)a,a′=#{x∣S(x+α)−S(x)=β}
矩阵的最大项
D
(
S
)
D(S)
D(S)定义为:
D
(
S
)
=
m
a
x
(
α
,
β
)
≠
{
0
,
0
}
Δ
(
S
)
α
,
β
D(S) = max_{(\alpha,\beta)\neq\{0,0\}} \Delta(S)_{\alpha,\beta}
D(S)=max(α,β)={0,0}Δ(S)α,β,则相应的最大差分概率定义为
D
P
(
S
)
=
D
(
s
)
/
q
DP(S)=D(s)/q
DP(S)=D(s)/q。
通过以上定义,我们可以知道
q
=
10
q=10
q=10我们计算出S盒的
q
×
q
q \times q
q×q矩阵
Δ
\Delta
Δ:
% MATLAB
S = [2 6 8 7 1 4 9 5 3 0]; %S盒
for i = 1:10 %行
for j = 1:10 %列
n = 0; %前面公式中的#表示符合条件的x的个数
for x = 1:10 %遍历x
% S(x+a)-S(x) = a'
if mod(S(mod(x+j-2,10)+1)-S(x),10) == i-1
n = n + 1;
end
end
N(i,j) = n;
end
end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
最后我们得出S盒的差分分布表:
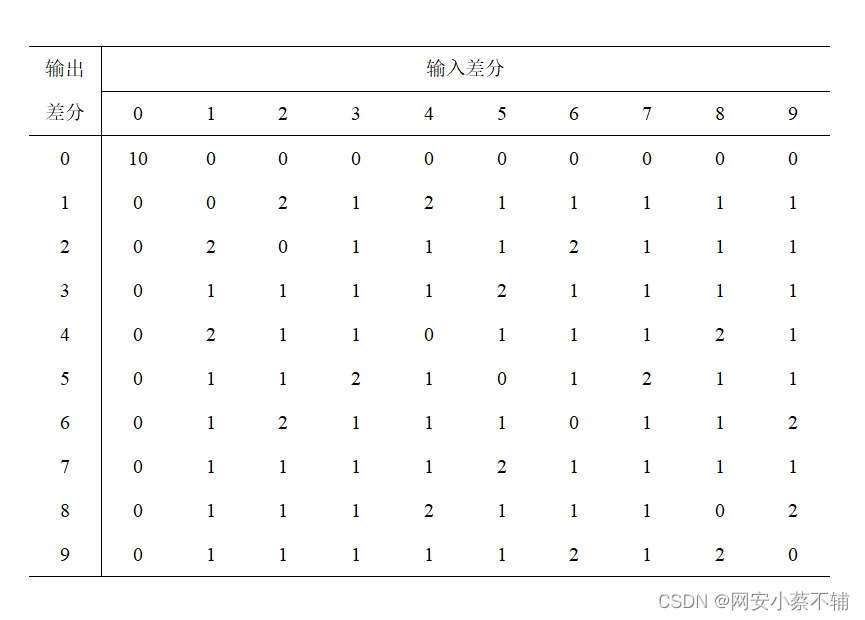
从表中可以看出,S盒的每一列之和为10,由上述公式所以我们可以得出
Δ
\Delta
Δ矩阵的最大项
D
(
S
)
=
2
D(S) = 2
D(S)=2,最大差分概率
D
P
(
S
)
=
D
(
S
)
/
q
=
2
−
2.3219
DP(S) = D(S)/q = 2^{-2.3219}
DP(S)=D(S)/q=2−2.3219,最大值差分值越小表明 S 盒的差分均匀性越好,抗差分攻击能力越强。可以看出此S盒的差分分布表相对来说是比较均匀的。
定义
P
S
(
α
→
β
)
=
Δ
(
S
)
α
,
β
/
q
P_S(\alpha \rarr \beta)=\Delta(S)_{\alpha, \beta}/q
PS(α→β)=Δ(S)α,β/q,即为输入差分
α
\alpha
α经过S盒后将以
P
S
(
α
→
β
)
P_S(\alpha \rarr \beta)
PS(α→β)的概率得到输出差分
β
\beta
β。如果
P
S
(
α
→
β
)
>
0
P_S(\alpha \rarr \beta)>0
PS(α→β)>0,则差分
α
\alpha
α经S盒可传播至差分
β
\beta
β,如果
P
S
(
α
→
β
)
=
0
P_S(\alpha \rarr \beta)=0
PS(α→β)=0,则差分
α
\alpha
α经S盒不能传播至差分
β
\beta
β。
知道了S盒的一组输入差分和输出差分 ( α , β ) (\alpha ,\beta) (α,β),我们就可以知道哪些具体的输入值 x x x会导致输入差分 α \alpha α传播至输出差分 β \beta β。
S盒的差分分布表实际上是研究满足特定差分的随机输入对经过S盒作用后输出对的差分分布特性。
2.2 S盒的差分分析
明文为 x x x,密钥为 k k k,密文为 y = S ( x + k ) y = S(x+k) y=S(x+k)。假设攻击者可以选择若干明文 x 1 , x 2 , . . . , x t x_1,x_2,... ,x_t x1,x2,...,xt,但不能获得相应的密文 y 1 , y 2 , . . . , y t y_1,y_2,... ,y_t y1,y2,...,yt,只能观察到某两个密文的差分,即攻击者可以获得若干三元数组 ( x i , x j , x i + x j ) (x_i,x_j,x_i+x_j) (xi,xj,xi+xj),并期望猜测密钥 k k k的若干信息。
对S盒的差分攻击主要利用了如下关键的性质: ( x + k ) − ( x ∗ + k ) = x + x ∗ (x+k) - (x^*+k) = x+x^* (x+k)−(x∗+k)=x+x∗,在这种攻击模型下面,要恢复密钥就要用到上面提到的
知道了S盒的一组输入差分和输出差分 ( α , β ) (\alpha ,\beta) (α,β),我们就可以知道哪些具体的输入值 x x x会导致输入差分 α \alpha α传播至输出差分 β \beta β。
下面详细的讲解这个攻击。
观察差分分布表,注意到当输入差分
α
=
1
\alpha=1
α=1时输出差分有8种可能,即
1
→
2
,
1
→
3
,
1
→
4
,
1
→
5
,
1
→
6
,
1
→
7
,
1
→
8
,
1
→
9
1 \rarr 2,1 \rarr 3,1 \rarr 4, 1 \rarr 5, \newline 1 \rarr 6, 1 \rarr 7, 1 \rarr 8, 1 \rarr 9
1→2,1→3,1→4,1→5,1→6,1→7,1→8,1→9
所以我们可以给出输入差分
α
=
1
\alpha=1
α=1时,输出差分
β
\beta
β的分布
| 输出差分 β \beta β | 关于 ( α , β ) 的 明 文 对 (\alpha,\beta)的明文对 (α,β)的明文对 | Δ ( S ) α , β \Delta(S)_{\alpha, \beta} Δ(S)α,β |
|---|---|---|
| 2 | 1, 9 | 2 |
| 3 | 4 | 1 |
| 4 | 0,3 | 2 |
| 5 | 5 | 1 |
| 6 | 6 | 1 |
| 7 | 8 | 1 |
| 8 | 7 | 1 |
| 9 | 2 | 1 |
| 其他 | ∅ \varnothing ∅ | 0 |
现在假设机密所采用的密钥是
k
=
4
k=4
k=4,加密过程如下:
若已知一对明文输入为
x
1
=
1
x_1 = 1
x1=1和
x
1
∗
=
2
x_1^* = 2
x1∗=2,则加密流程为
x
1
=
1
,
z
1
=
x
1
+
k
(
m
o
d
10
)
=
5
,
y
1
=
S
(
z
1
)
=
4
x_1 = 1, z_1 = x_1 +k \pmod {10}=5,y_1=S(z_1)=4
x1=1,z1=x1+k(mod10)=5,y1=S(z1)=4
x
1
∗
=
2
,
z
1
∗
=
x
1
∗
+
k
(
m
o
d
10
)
=
6
,
y
1
∗
=
S
(
z
1
∗
)
=
9
x_1^* = 2, z_1^* = x_1^* +k \pmod {10}=6,y_1^*=S(z_1^*)=9
x1∗=2,z1∗=x1∗+k(mod10)=6,y1∗=S(z1∗)=9
此时输出差分
Δ
y
1
=
5
\Delta y_1=5
Δy1=5
现假设攻击者获取一对明文输入
x
1
=
1
x_1 = 1
x1=1和
x
1
∗
=
2
x_1^* = 2
x1∗=2,但只能观察到对应的密文对的输出差分
Δ
y
1
=
5
\Delta y_1=5
Δy1=5,根据输出差分想得到密钥
k
k
k的消息:首先明文差分
Δ
x
1
=
x
1
−
x
1
∗
=
1
\Delta x_1=x_1-x_1^*=1
Δx1=x1−x1∗=1,则S盒的输入差分
Δ
z
1
=
z
1
+
z
1
∗
=
1
\Delta z_1=z_1+z_1^* = 1
Δz1=z1+z1∗=1,根据表中的信息:
1
→
5
1 \rarr 5
1→5当且仅当
z
1
=
x
1
+
k
∈
{
5
}
z_1 = x_1 +k \in \{5\}
z1=x1+k∈{5},这样就会得到
k
k
k的一组候选值,即
k
=
z
1
−
x
1
∈
{
4
}
k=z_1-x_1\in \{4\}
k=z1−x1∈{4},这样直接把密钥破解出来了。
对于大型的S盒,多选择几对明文对,使用相同的密钥,得出密钥
k
k
k的另外几组候选值,我们可以知道,正确的密钥一定落在上述几组候选密钥的交集中,这样可以缩小密钥的范围。但如果只采用差分分布表中的某一列的信息,可能不能唯一的确定正确密钥,为了获得唯一的正确密钥,可以选择差分分布表中不同列的消息。
根据以上我们可以看出,S盒越大越好,小的S盒很容易被破解。
总结
差分密码分析是方法是攻击迭代型分组密码的最有效的方式之一,也是最基础的一种密码分析手段,同时也是衡量一个分组密码安全性的重要指标之一。差分密码分析的原理比较简单,发展至今,该方法出现了很多的变种,但万变不离其宗,本质上就是研究差分在加解密过程中的概率传播特性。
本文仅仅列出了破解简单S盒的一个实例,而且S盒只有一轮,如果有时间,会更新!!!!!
希望对阅读本文的小伙伴们有帮助,如果有什么错误或者问题,欢迎大家评论转发!!!!!!
参考文献
Lai X . Markov Ciphers and Differential Cryptanalysis[J]. Advances in Cryptography-EUROCRYPTO '91, 1992. ↩︎
Granboulan L, Levieil E´, Piret G (2006) Pseudorandom per-mutation families over Abelian groups. In: Robshaw MJB (ed)Fast software encryption, 13th international workshop, FSE 2006,Graz, Austria, March 15–17, 2006, Revised Selected Papers, Lecture Notes in Computer Science, vol 4047. Springer, pp 57–77 ↩︎


