热门标签
当前位置: article > 正文
机器学习算法中GBDT和XGBOOST_基于gbdt和xgboost的预测模型
作者:Gausst松鼠会 | 2024-05-03 02:42:46
赞
踩
基于gbdt和xgboost的预测模型
1.引言
最近,因为一些原因,自己需要做一个小范围的XGBoost的实现层面的分享,于是干脆就整理了一下相关的资料,串接出了这份report,也算跟这里的问题相关,算是从一个更偏算法实现的角度,提供一份参考资料吧。
这份report从建模原理、单机实现、分布式实现这几个角度展开。
在切入到细节之前,特别提一下,对于有过GBDT算法实现经验的同学(与我有过直接connection的同学,至少有将四位同学都有过直接实现GBDT算法的经验)来说,这份report可能不会有太多新意,这更多是一个技术细节的梳理,一来用作技术分享的素材,二来也是顺便整理一下自己对这个问题的理解,因为自己实际上并没有亲自动手实现过分布式的GBDT算法,所以希望借这个机会也来梳理一下相关的知识体系。
本文基于XGBoost官网代码[12]。
最近,因为一些原因,自己需要做一个小范围的XGBoost的实现层面的分享,于是干脆就整理了一下相关的资料,串接出了这份report,也算跟这里的问题相关,算是从一个更偏算法实现的角度,提供一份参考资料吧。
这份report从建模原理、单机实现、分布式实现这几个角度展开。
在切入到细节之前,特别提一下,对于有过GBDT算法实现经验的同学(与我有过直接connection的同学,至少有将四位同学都有过直接实现GBDT算法的经验)来说,这份report可能不会有太多新意,这更多是一个技术细节的梳理,一来用作技术分享的素材,二来也是顺便整理一下自己对这个问题的理解,因为自己实际上并没有亲自动手实现过分布式的GBDT算法,所以希望借这个机会也来梳理一下相关的知识体系。
本文基于XGBoost官网代码[12]。
2.建模原理
我个人的理解,从算法实现的角度,把握一个机器学习算法的关键点有两个,一个是loss function的理解(包括对特征X/标签Y配对的建模,以及基于X/Y配对建模的loss function的设计,前者应用于inference,后者应用于training,而前者又是后者的组成部分),另一个是对求解过程的把握。这两个点串接在一起构成了算法实现的主框架。具体到XGBoost,也不出其外。
XGBoost的loss function可以拆解为两个部分,第一部分是X/Y配对的建模,第二部分是基于X/Y建模的loss function的设计。
2.1. X/Y建模
作为GBDT算法的具体实现,XGBoost代表了Tree Model的一个特例(boosting tree v.s. bagging tree),基本的思想用下图描述起来会更为直观:
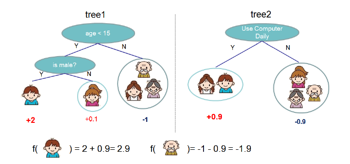
我个人的理解,从算法实现的角度,把握一个机器学习算法的关键点有两个,一个是loss function的理解(包括对特征X/标签Y配对的建模,以及基于X/Y配对建模的loss function的设计,前者应用于inference,后者应用于training,而前者又是后者的组成部分),另一个是对求解过程的把握。这两个点串接在一起构成了算法实现的主框架。具体到XGBoost,也不出其外。
XGBoost的loss function可以拆解为两个部分,第一部分是X/Y配对的建模,第二部分是基于X/Y建模的loss function的设计。
2.1. X/Y建模
作为GBDT算法的具体实现,XGBoost代表了Tree Model的一个特例(boosting tree v.s. bagging tree),基本的思想用下图描述起来会更为直观:

如果从形式化的角度来观察,则可以描述如下:

其中F代表一个泛函,表征决策树的函数空间,K表示构成GBDT模型的Tree的个数,T表示一个决策树的叶子结点的数目, w是一个向量。
看到上面X/Y的建模方式,也许我们会有一个疑问:上面的建模方式输出的会是一个浮点标量,这种建模方式,对于Regression Problem拟合得很自然,但是对于classification问题,怎样将浮点标量与离散分类问题联系起来呢?
理解这个问题,实际上,可以通过Logistic Regression分类模型来获得启发。
我们知道,LR模型的建模形式,输出的也会是一个浮点数,这个浮点数又是怎样跟离散分类问题(分类面)联系起来的呢?实际上,从广义线性模型[13]的角度,待学习的分类面建模的实际上是Logit[3],Logit本身是是由LR预测的浮点数结合建模目标满足Bernoulli分布来表征的,数学形式如下:

对上面这个式子做一下数学变换,能够得出下面的形式:

这样一来,我们实际上将模型的浮点预测值与离散分类问题建立起了联系。
相同的建模技巧套用到GBDT里,也就找到了树模型的浮点预测值与离散分类问题的联系:

考虑到GBDT应用于分类问题的建模更为tricky一些,所以后续关于loss function以及实现的讨论都会基于GBDT在分类问题上的展开,后续不再赘述。
2.2. Loss Function设计
分类问题的典型Loss建模方式是基于极大似然估计,具体到每个样本上,实际上就是典型的二项分布概率建模式[1]:

经典的极大似然估计是基于每个样本的概率连乘,这种形式不利于求解,所以,通常会通过取对数来将连乘变为连加,将指数变为乘法,所以会有下面的形式:

再考虑到loss function的数值含义是最优点对应于最小值点,所以,对似然估计取一下负数,即得到最终的loss形式,这也是经典的logistic loss[2]:

有了每个样本的Loss,样本全集上的Loss形式也就不难构造出来:

2.3. 求解算法
GBDT的求解算法,具体到每颗树来说,其实就是不断地寻找分割点(split point),将样本集进行分割,初始情况下,所有样本都处于一个结点(即根结点),随着树的分裂过程的展开,样本会
分配到分裂开的子结点上。分割点的选择通过枚举训练样本集上的特征值来完成,分割点的选择依据则是减少Loss。
给定一组样本,实际上存在指数规模的分割方式,所以这是一个NP-Hard的问题,实际的求解算法也没有办法在多项式时间内完成求解,而是采用一种基于贪心原则的启发式方法来完成求解。 也就是说,在选取分割点的时候,只考虑当前树结构到下一步树结构的loss变化的最优值,不考虑树分裂的多个步骤之间的最优值,这是典型的greedy的策略。
在XGBoost的实现, 为了便于求解,对loss function基于Taylor Expansion进行了变换:


在变换完之后的形式里, 就是为了优化loss function,待更新优化的变量(这里的变量是一个广义的描述)。
就是为了优化loss function,待更新优化的变量(这里的变量是一个广义的描述)。
上面的loss function是针对一个样本而言的,所以,对于样本全集来说,loss function的形式是:


对这个loss function进行优化的过程,实际上就是对第k个树结构进行分裂,找到启发式的最优树结构的过程。而每次分裂,对应于将属于一个叶结点(初始情况下只有一个叶结点,即根结点)下的训练样本分配到分裂出的两个新叶结点上,每个叶结点上的训练样本都会对应一个模型学出的概率值,而loss function本身满足样本之间的累加特性,所以,可以通过将分裂前的叶结点上样本的loss function和与分裂之后的两个新叶结点上的样本的loss function之和进行对比,从而找到可用的分裂特征以及特征分裂点。
而每个叶结点上都会附著一个weight,这个weight会用于对落在这个叶结点上的样本打分使用,所以叶结点weight的赋值,也会影响到loss function的变化。基于这种考虑,也许将loss function从样本维度转移到叶结点维度也许更为自然,于是就有了下面的形式:

上面的loss function,本质上是一个包含T(T对应于Tree当前的叶子结点的个数)个自变量的二次函数,这也是一个convex function,所以,可以通过求函数极值点的方式获得最优解析解(偏导数为0的点对应于极值点),其形如下:

现在,我们可以把求解过程串接梳理一下:
I. 对loss function进行二阶Taylor Expansion,展开以后的形式里,当前待学习的Tree是变量,需要进行优化求解。
II. Tree的优化过程,包括两个环节:
I). 枚举每个叶结点上的特征潜在的分裂点
II). 对每个潜在的分裂点,计算如果以这个分裂点对叶结点进行分割以后,分割前和分割后的loss function的变化情况。
因为Loss Function满足累积性(对MLE取log的好处),并且每个叶结点对应的weight的求取是独立于其他叶结点的(只跟落在这个叶结点上的样本有关),所以,不同叶结点上的loss function满足单调累加性,只要保证每个叶结点上的样本累积loss function最小化,整体样本集的loss function也就最小化了。
而给定一个叶结点,可以通过求取解析解计算出这个叶结点上样本集的loss function最小值。
有了上面的两个环节,就可以找出基于当前树结构,最优的分裂点,完成Tree结构的优化。
这就是完整的求解思路。有了这个求解思路的介绍,我们就可以切入到具体实现细节了。
注意,实际的求解过程中,为了避免过拟合,会在Loss Function加入对叶结点weight以及叶结点个数的正则项,所以具体的优化细节会有微调,不过这已经不再影响问题的本质,所以此处不再展开介绍。
3.单机实现
有了2里对XGBoost算法原理的介绍,不难推敲出单机的实现细节。实际上,对XGBoost的源码进行走读分析之后,从其代码主流程可以看到,
其中F代表一个泛函,表征决策树的函数空间,K表示构成GBDT模型的Tree的个数,T表示一个决策树的叶子结点的数目, w是一个向量。
看到上面X/Y的建模方式,也许我们会有一个疑问:上面的建模方式输出的会是一个浮点标量,这种建模方式,对于Regression Problem拟合得很自然,但是对于classification问题,怎样将浮点标量与离散分类问题联系起来呢?
理解这个问题,实际上,可以通过Logistic Regression分类模型来获得启发。
我们知道,LR模型的建模形式,输出的也会是一个浮点数,这个浮点数又是怎样跟离散分类问题(分类面)联系起来的呢?实际上,从广义线性模型[13]的角度,待学习的分类面建模的实际上是Logit[3],Logit本身是是由LR预测的浮点数结合建模目标满足Bernoulli分布来表征的,数学形式如下:
对上面这个式子做一下数学变换,能够得出下面的形式:
这样一来,我们实际上将模型的浮点预测值与离散分类问题建立起了联系。
相同的建模技巧套用到GBDT里,也就找到了树模型的浮点预测值与离散分类问题的联系:
考虑到GBDT应用于分类问题的建模更为tricky一些,所以后续关于loss function以及实现的讨论都会基于GBDT在分类问题上的展开,后续不再赘述。
2.2. Loss Function设计
分类问题的典型Loss建模方式是基于极大似然估计,具体到每个样本上,实际上就是典型的二项分布概率建模式[1]:
经典的极大似然估计是基于每个样本的概率连乘,这种形式不利于求解,所以,通常会通过取对数来将连乘变为连加,将指数变为乘法,所以会有下面的形式:
再考虑到loss function的数值含义是最优点对应于最小值点,所以,对似然估计取一下负数,即得到最终的loss形式,这也是经典的logistic loss[2]:
有了每个样本的Loss,样本全集上的Loss形式也就不难构造出来:
2.3. 求解算法
GBDT的求解算法,具体到每颗树来说,其实就是不断地寻找分割点(split point),将样本集进行分割,初始情况下,所有样本都处于一个结点(即根结点),随着树的分裂过程的展开,样本会
分配到分裂开的子结点上。分割点的选择通过枚举训练样本集上的特征值来完成,分割点的选择依据则是减少Loss。
给定一组样本,实际上存在指数规模的分割方式,所以这是一个NP-Hard的问题,实际的求解算法也没有办法在多项式时间内完成求解,而是采用一种基于贪心原则的启发式方法来完成求解。 也就是说,在选取分割点的时候,只考虑当前树结构到下一步树结构的loss变化的最优值,不考虑树分裂的多个步骤之间的最优值,这是典型的greedy的策略。
在XGBoost的实现, 为了便于求解,对loss function基于Taylor Expansion进行了变换:
在变换完之后的形式里,
上面的loss function是针对一个样本而言的,所以,对于样本全集来说,loss function的形式是:
对这个loss function进行优化的过程,实际上就是对第k个树结构进行分裂,找到启发式的最优树结构的过程。而每次分裂,对应于将属于一个叶结点(初始情况下只有一个叶结点,即根结点)下的训练样本分配到分裂出的两个新叶结点上,每个叶结点上的训练样本都会对应一个模型学出的概率值,而loss function本身满足样本之间的累加特性,所以,可以通过将分裂前的叶结点上样本的loss function和与分裂之后的两个新叶结点上的样本的loss function之和进行对比,从而找到可用的分裂特征以及特征分裂点。
而每个叶结点上都会附著一个weight,这个weight会用于对落在这个叶结点上的样本打分使用,所以叶结点weight的赋值,也会影响到loss function的变化。基于这种考虑,也许将loss function从样本维度转移到叶结点维度也许更为自然,于是就有了下面的形式:
上面的loss function,本质上是一个包含T(T对应于Tree当前的叶子结点的个数)个自变量的二次函数,这也是一个convex function,所以,可以通过求函数极值点的方式获得最优解析解(偏导数为0的点对应于极值点),其形如下:
现在,我们可以把求解过程串接梳理一下:
I. 对loss function进行二阶Taylor Expansion,展开以后的形式里,当前待学习的Tree是变量,需要进行优化求解。
II. Tree的优化过程,包括两个环节:
I). 枚举每个叶结点上的特征潜在的分裂点
II). 对每个潜在的分裂点,计算如果以这个分裂点对叶结点进行分割以后,分割前和分割后的loss function的变化情况。
因为Loss Function满足累积性(对MLE取log的好处),并且每个叶结点对应的weight的求取是独立于其他叶结点的(只跟落在这个叶结点上的样本有关),所以,不同叶结点上的loss function满足单调累加性,只要保证每个叶结点上的样本累积loss function最小化,整体样本集的loss function也就最小化了。
而给定一个叶结点,可以通过求取解析解计算出这个叶结点上样本集的loss function最小值。
有了上面的两个环节,就可以找出基于当前树结构,最优的分裂点,完成Tree结构的优化。
这就是完整的求解思路。有了这个求解思路的介绍,我们就可以切入到具体实现细节了。
注意,实际的求解过程中,为了避免过拟合,会在Loss Function加入对叶结点weight以及叶结点个数的正则项,所以具体的优化细节会有微调,不过这已经不再影响问题的本质,所以此处不再展开介绍。
3.单机实现
有了2里对XGBoost算法原理的介绍,不难推敲出单机的实现细节。实际上,对XGBoost的源码进行走读分析之后,从其代码主流程可以看到,
在XGBoost的实现中,对算法进行了模块化的拆解,几个重要的部分分别是:
I. ObjFunction:对应于不同的Loss Function,可以完成一阶和二阶导数的计算。
II. GradientBooster:用于管理Boost方法生成的Model,注意,这里的Booster Model既可以对应于线性Booster Model,也可以对应于Tree Booster Model。
III. Updater:用于建树,根据具体的建树策略不同,也会有多种Updater。比如,在XGBoost里为了性能优化,既提供了单机多线程并行加速,也支持多机分布式加速。也就提供了若干种不同的并行建树的updater实现,按并行策略的不同,包括:
I). inter-feature exact parallelism (特征级精确并行)
II). inter-feature approximate parallelism(特征级近似并行,基于特征分bin计算,减少了枚举所有特征分裂点的开销)
III). intra-feature parallelism (特征内并行)
IV). inter-node parallelism (多机并行)
此外,为了避免overfit,还提供了一个用于对树进行剪枝的updater(TreePruner),以及一个用于在分布式场景下完成结点模型参数信息通信的updater(TreeSyncher),这样设计,关于建树的主要操作都可以通过Updater链的方式串接起来,比较一致干净,算是Decorator设计模式[4]的一种应用。
XGBoost的实现中,最重要的就是建树环节,而建树对应的代码中,最主要的也是Updater的实现。所以我们会以Updater的实现作为介绍的入手点。
以ColMaker(单机版的inter-feature parallelism,实现了精确建树的策略)为例,其建树操作大致过程,稍微抽象成流程图描述,如下:
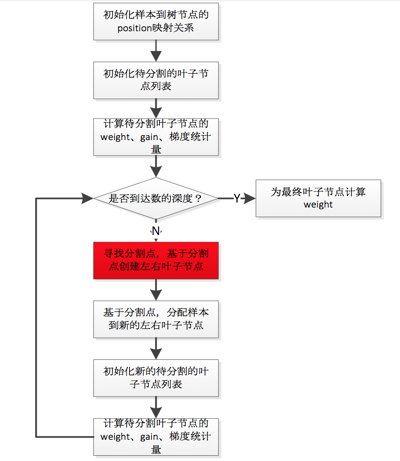
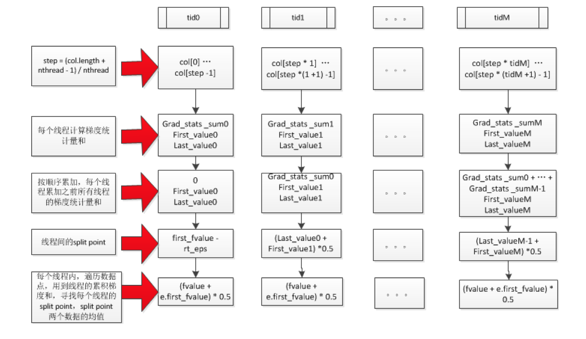
ColMaker的整个建树操作中,最tricky的地方应该是用于支持intra-feature parallelism的ParallelFindSplit(),关于这个计算逻辑,上面有一些文字描述,辅助下图可能会更为直观:
转载来源:
来源:知乎
作者:杨军
链接:https://www.zhihu.com/question/41354392/answer/124274741
II. GradientBooster:用于管理Boost方法生成的Model,注意,这里的Booster Model既可以对应于线性Booster Model,也可以对应于Tree Booster Model。
III. Updater:用于建树,根据具体的建树策略不同,也会有多种Updater。比如,在XGBoost里为了性能优化,既提供了单机多线程并行加速,也支持多机分布式加速。也就提供了若干种不同的并行建树的updater实现,按并行策略的不同,包括:
I). inter-feature exact parallelism (特征级精确并行)
II). inter-feature approximate parallelism(特征级近似并行,基于特征分bin计算,减少了枚举所有特征分裂点的开销)
III). intra-feature parallelism (特征内并行)
IV). inter-node parallelism (多机并行)
此外,为了避免overfit,还提供了一个用于对树进行剪枝的updater(TreePruner),以及一个用于在分布式场景下完成结点模型参数信息通信的updater(TreeSyncher),这样设计,关于建树的主要操作都可以通过Updater链的方式串接起来,比较一致干净,算是Decorator设计模式[4]的一种应用。
XGBoost的实现中,最重要的就是建树环节,而建树对应的代码中,最主要的也是Updater的实现。所以我们会以Updater的实现作为介绍的入手点。
以ColMaker(单机版的inter-feature parallelism,实现了精确建树的策略)为例,其建树操作大致过程,稍微抽象成流程图描述,如下:

ColMaker的整个建树操作中,最tricky的地方应该是用于支持intra-feature parallelism的ParallelFindSplit(),关于这个计算逻辑,上面有一些文字描述,辅助下图可能会更为直观:

以上是我对XGBoost单机多线程的精确建树算法的整理,在[5]的官方论文里,对于这个算法有一个更为凝炼形式化的表达:
 单机版本的实现中,另一个比较重要的细节是对于稀疏离散特征的支持,在这方面,XGBoost的实现还是做了比较细致的工程优化考量,在[5]里对这个支持也提供了完整的描述:
单机版本的实现中,另一个比较重要的细节是对于稀疏离散特征的支持,在这方面,XGBoost的实现还是做了比较细致的工程优化考量,在[5]里对这个支持也提供了完整的描述:

稍微解读一下的话,在XGBoost里,对于稀疏性的离散特征,在寻找split point的时候,不会对该特征为missing的样本进行遍历统计,只对该列特征值为non-missing的样本上对应的特征值进行遍历,通过这个工程trick来减少了为稀疏离散特征寻找split point的时间开销。在逻辑实现上,为了保证完备性,会分别处理将missing该特征值的样本分配到左叶子结点和右叶子结点的两种情形。
在XGBoost里,单机多线程,并没有通过显式的pthread这样的方式来实现,而是通过OpenMP[6]来完成多线程的处理,我个人的理解,这可能跟XGBoost里多线程的处理逻辑相对简单,没有复杂的线程之间同步的需要,所以通过OpenMP可以支持得比较好,也简化了代码的开发和维护负担。
单机实现中,另一个重要的updater是TreePruner,这是一个为了减少overfit,在loss函数的正则项之外提供的额外正则化手段,实现逻辑也比较直观,对于已经构造好的Tree结构,判断每个叶子结点,如果这个叶子结点的父结点分裂所带来的loss变化小于配置文件中规定的阈值,就会把这个叶子结点和它的兄弟结点合并回父结点里,并且这个pruning操作会递归下去。
上面介绍的是精确的建模算法,在XGBoost中,出于性能优化的考虑,也提供了近似的建模算法支持,核心思想是在寻找split point的时候,不会枚举所有的特征值,而会对特征值进行聚合统计,然后形成若干个bucket,只将bucket边界上的特征值作为split point的候选,从而获得性能提升。

关于近似算法的实现细节,我并没有深入阅读,所以在此就不再介绍。
4.分布式实现
关于XGBoost的分布式实现,一共提供了两种支持,一种基于RABIT[7],另一种则基于Spark[8]。其中XGBoost4j的底层通信实际上还是用到了RABIT。
从我个人阅读代码和相关文档的理解来看,Distributed XGBoost里针对核心算法分布式的主要逻辑还是基于RABIT完成的,XGBoost4j更像是在RABIT-based XGBoost上做了一层wrapper,工程量并不小,但是涉及到XGBoost核心算法的分布式细节并不多,所以后续的介绍,我也会主要cover基于RABIT的 XGBoost分布式实现。
把握Distributed XGBoost,需要从计算任务的调度管理和核心算法分布式实现这两个角度展开。
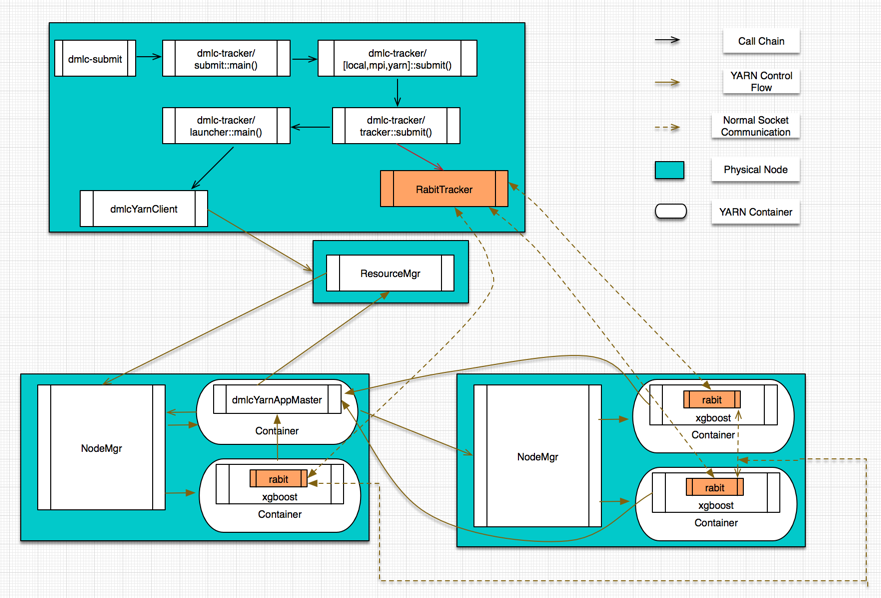
计算任务的调度管理,在RABIT里提供了native MPI/Sun Grid Engine/YARN这三种方式。Sun Grid Engine因为我手上没有现成的环境,所以没有关注。native MPI这种方式,实际上除了计算任务的调度管理以外,也提供了相应的通信原语(在RABIT里,针对native MPI这种任务管理方式,只是在MPI_allreduce[14]/MPI_broadcast[15]这两个通信原语上做了一层简单的wrapper),所以更像一个纯粹的MPI计算任务,在这里我也不打算详述。XGboost on YARN这种模式涉及到的细节则最多,包括YARN ApplicationMaster/Client的开发、Tracker脚本的开发、RABIT容错通信原语的开发以及基于RABIT原语的XGBoost算法分布式实现,会是我介绍的重点。下面这张鸟噉图有助于建立起XGBoost on YARN的整体认识。
 单机版本的实现中,另一个比较重要的细节是对于稀疏离散特征的支持,在这方面,XGBoost的实现还是做了比较细致的工程优化考量,在[5]里对这个支持也提供了完整的描述:
单机版本的实现中,另一个比较重要的细节是对于稀疏离散特征的支持,在这方面,XGBoost的实现还是做了比较细致的工程优化考量,在[5]里对这个支持也提供了完整的描述:

稍微解读一下的话,在XGBoost里,对于稀疏性的离散特征,在寻找split point的时候,不会对该特征为missing的样本进行遍历统计,只对该列特征值为non-missing的样本上对应的特征值进行遍历,通过这个工程trick来减少了为稀疏离散特征寻找split point的时间开销。在逻辑实现上,为了保证完备性,会分别处理将missing该特征值的样本分配到左叶子结点和右叶子结点的两种情形。
在XGBoost里,单机多线程,并没有通过显式的pthread这样的方式来实现,而是通过OpenMP[6]来完成多线程的处理,我个人的理解,这可能跟XGBoost里多线程的处理逻辑相对简单,没有复杂的线程之间同步的需要,所以通过OpenMP可以支持得比较好,也简化了代码的开发和维护负担。
单机实现中,另一个重要的updater是TreePruner,这是一个为了减少overfit,在loss函数的正则项之外提供的额外正则化手段,实现逻辑也比较直观,对于已经构造好的Tree结构,判断每个叶子结点,如果这个叶子结点的父结点分裂所带来的loss变化小于配置文件中规定的阈值,就会把这个叶子结点和它的兄弟结点合并回父结点里,并且这个pruning操作会递归下去。
上面介绍的是精确的建模算法,在XGBoost中,出于性能优化的考虑,也提供了近似的建模算法支持,核心思想是在寻找split point的时候,不会枚举所有的特征值,而会对特征值进行聚合统计,然后形成若干个bucket,只将bucket边界上的特征值作为split point的候选,从而获得性能提升。

关于近似算法的实现细节,我并没有深入阅读,所以在此就不再介绍。
4.分布式实现
关于XGBoost的分布式实现,一共提供了两种支持,一种基于RABIT[7],另一种则基于Spark[8]。其中XGBoost4j的底层通信实际上还是用到了RABIT。
从我个人阅读代码和相关文档的理解来看,Distributed XGBoost里针对核心算法分布式的主要逻辑还是基于RABIT完成的,XGBoost4j更像是在RABIT-based XGBoost上做了一层wrapper,工程量并不小,但是涉及到XGBoost核心算法的分布式细节并不多,所以后续的介绍,我也会主要cover基于RABIT的 XGBoost分布式实现。
把握Distributed XGBoost,需要从计算任务的调度管理和核心算法分布式实现这两个角度展开。
计算任务的调度管理,在RABIT里提供了native MPI/Sun Grid Engine/YARN这三种方式。Sun Grid Engine因为我手上没有现成的环境,所以没有关注。native MPI这种方式,实际上除了计算任务的调度管理以外,也提供了相应的通信原语(在RABIT里,针对native MPI这种任务管理方式,只是在MPI_allreduce[14]/MPI_broadcast[15]这两个通信原语上做了一层简单的wrapper),所以更像一个纯粹的MPI计算任务,在这里我也不打算详述。XGboost on YARN这种模式涉及到的细节则最多,包括YARN ApplicationMaster/Client的开发、Tracker脚本的开发、RABIT容错通信原语的开发以及基于RABIT原语的XGBoost算法分布式实现,会是我介绍的重点。下面这张鸟噉图有助于建立起XGBoost on YARN的整体认识。

在这个图里,有几个重要的角色,分别介绍一下。
I. Tracker:这其实是一个Python写的脚本程序,主要完成的工作有
I). 启动daemon服务,提供worker结点注册联接所需的end point,所有的worker结点都可以通过与Tracker程序通信来完成自身状态信息的注册
II). co-ordinate worker结点的执行:
为worker结点分配Rank编号。
基于收到的worker注册信息完成网络结构的构建,并广播给worker结点,以确保worker结点之间建立起合规的网络拓扑。
当所有的worker结点都建立起完备的网络拓扑关系以后,就可以启动计算任务监控整个执行过程。
II. Application Master:这其实是基于YARN AM接口的一个实现[9],完成的就是常规的YARN Application Master的功能,此处不再多述。
III. Client:这其实是基于YARN Client接口的一个实现[10]。
IV. Worker:对应于实际的计算任务,本质上,每个worker结点(在YARN里应该称之为一个容器,因为一个结点上可以启动多个YARN容器)里都会启动一个XGBoost进程。这些XGBoost进程在初始化阶段,会通过与Tracker之间通信,完成自身信息的注册,同时会从Tracker里获取到完整的网络结构信息,从而完成通信所需的网络拓扑结构的构建。
V. RABIT Library[11]:RABIT实现的通信原语,目前只支持allreduce和broadcast这两个原语,并且提供了一定的fault-tolerance支持(RABIT通信框架中存在Tracker这个单点,所以只能在一定程度上支持Worker上的错误异常,基本的实现套路是,基于YARN的failure recovery机制,对于transient network error以及硬件down机这样的异常都提供了一定程度的支持)。
VI. XGBoost Process:在单机版的逻辑之外,还提供了用于Worker之间通信的相关逻辑,主要的通信数据包括:
树模型的最新参数(从Rank 0结点到其他结点)
每次分裂叶子结点时,为了计算最优split point,所需从各个结点汇总的统计量,包括近似算法里为了propose split point所需的bucket信息、训练样本的梯度信息等(从其他结点到Rank 0结点)
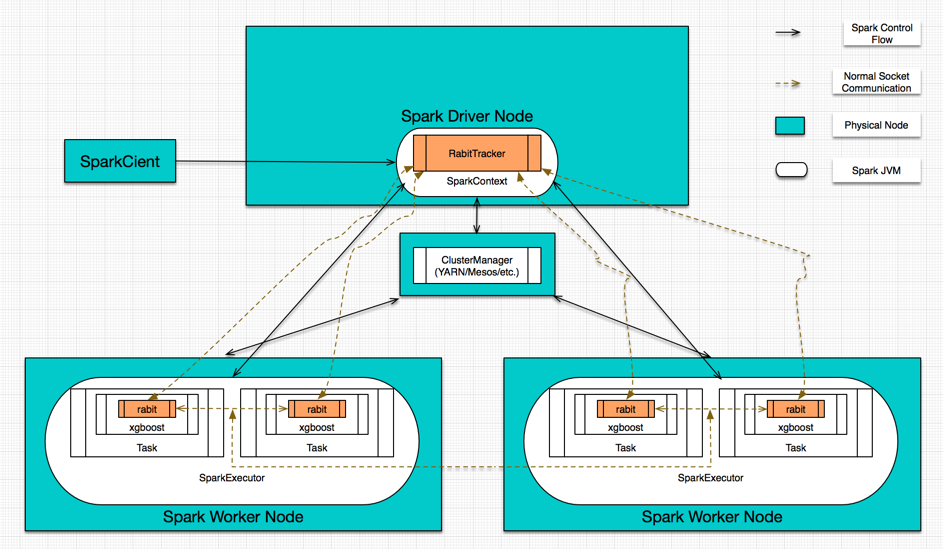
XGBoost4j的实现,我就不再详述,本质上就是一个XGBoost YARN的Spark wrapper,直接附上当初梳理XGBoost4j所画的一个示意图:
I. Tracker:这其实是一个Python写的脚本程序,主要完成的工作有
I). 启动daemon服务,提供worker结点注册联接所需的end point,所有的worker结点都可以通过与Tracker程序通信来完成自身状态信息的注册
II). co-ordinate worker结点的执行:
为worker结点分配Rank编号。
基于收到的worker注册信息完成网络结构的构建,并广播给worker结点,以确保worker结点之间建立起合规的网络拓扑。
当所有的worker结点都建立起完备的网络拓扑关系以后,就可以启动计算任务监控整个执行过程。
II. Application Master:这其实是基于YARN AM接口的一个实现[9],完成的就是常规的YARN Application Master的功能,此处不再多述。
III. Client:这其实是基于YARN Client接口的一个实现[10]。
IV. Worker:对应于实际的计算任务,本质上,每个worker结点(在YARN里应该称之为一个容器,因为一个结点上可以启动多个YARN容器)里都会启动一个XGBoost进程。这些XGBoost进程在初始化阶段,会通过与Tracker之间通信,完成自身信息的注册,同时会从Tracker里获取到完整的网络结构信息,从而完成通信所需的网络拓扑结构的构建。
V. RABIT Library[11]:RABIT实现的通信原语,目前只支持allreduce和broadcast这两个原语,并且提供了一定的fault-tolerance支持(RABIT通信框架中存在Tracker这个单点,所以只能在一定程度上支持Worker上的错误异常,基本的实现套路是,基于YARN的failure recovery机制,对于transient network error以及硬件down机这样的异常都提供了一定程度的支持)。
VI. XGBoost Process:在单机版的逻辑之外,还提供了用于Worker之间通信的相关逻辑,主要的通信数据包括:
树模型的最新参数(从Rank 0结点到其他结点)
每次分裂叶子结点时,为了计算最优split point,所需从各个结点汇总的统计量,包括近似算法里为了propose split point所需的bucket信息、训练样本的梯度信息等(从其他结点到Rank 0结点)
XGBoost4j的实现,我就不再详述,本质上就是一个XGBoost YARN的Spark wrapper,直接附上当初梳理XGBoost4j所画的一个示意图:

从上图可以看出,在XGBoost4j里,XGBoost的分布式逻辑其实还是通过RABIT来完成的,并且是通过RabitTracker完成任务的co-ordination。
以上是我对XGBoost的设计&实现的一些剖析,供参考。
References:
[1]. Bernoulli Distribution. Bernoulli distribution
[2]. Logistic Loss. Loss functions for classification
[3]. Logit. Logit
[4]. Decorator Pattern. Decorator pattern
[5]. Tianqi Chen. XGBoost: A Scalable Tree Boosting System. KDD, 2016.
[6]. OpenMP. OpenMP
[7]. RABIT. https://github.com/dmlc/rabit
[8]. XGBoost4j. xgboost/jvm-packages at master · dmlc/xgboost · GitHub
[9]. Writing an Application Master. Apache Hadoop 3.0.0-alpha1
[10]. Writing a Simple Client. Apache Hadoop 3.0.0-alpha1
[11]. Tianqi Chen. RABIT: A Reliable Allreduce and Broadcast Interface.
[12]. XGBoost. GitHub - dmlc/xgboost: Scalable, Portable and Distributed Gradient Boosting (GBDT, GBRT or GBM) Library, for Python, R, Java, Scala, C++ and more. Runs on single machine, Hadoop, Spark, Flink and DataFlow
[13]. Generalized Linear Model. Generalized linear model
[14]. MPI_Allreduce. MPI_Allreduce
[15]. MPI_Bcast. MPI_Bcast
以上是我对XGBoost的设计&实现的一些剖析,供参考。
References:
[1]. Bernoulli Distribution. Bernoulli distribution
[2]. Logistic Loss. Loss functions for classification
[3]. Logit. Logit
[4]. Decorator Pattern. Decorator pattern
[5]. Tianqi Chen. XGBoost: A Scalable Tree Boosting System. KDD, 2016.
[6]. OpenMP. OpenMP
[7]. RABIT. https://github.com/dmlc/rabit
[8]. XGBoost4j. xgboost/jvm-packages at master · dmlc/xgboost · GitHub
[9]. Writing an Application Master. Apache Hadoop 3.0.0-alpha1
[10]. Writing a Simple Client. Apache Hadoop 3.0.0-alpha1
[11]. Tianqi Chen. RABIT: A Reliable Allreduce and Broadcast Interface.
[12]. XGBoost. GitHub - dmlc/xgboost: Scalable, Portable and Distributed Gradient Boosting (GBDT, GBRT or GBM) Library, for Python, R, Java, Scala, C++ and more. Runs on single machine, Hadoop, Spark, Flink and DataFlow
[13]. Generalized Linear Model. Generalized linear model
[14]. MPI_Allreduce. MPI_Allreduce
[15]. MPI_Bcast. MPI_Bcast
转载来源:
来源:知乎
作者:杨军
链接:https://www.zhihu.com/question/41354392/answer/124274741
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/Gausst松鼠会/article/detail/527388
推荐阅读
相关标签


