基于ITD的特征提取_itd算法

      HHT的过程本征模态分解EMD存在严重的端点效应，分解过程需要多次迭代运算，运算量大、效率低；且产生一些原信号中不存在的频率成分，显示信号动态性方面存在不足，这些都影响了该方法在SEI中的效果。

       FREI等提出了固有时间尺度分解(ITD, intrinsic time-scale decomposition)算法，该方法克服了EMD在信号边界和计算效率上的缺点，通过对信号自适应划分，得到若干个有实际意义的信号分量，有效提升时频分析的效率与精度，更适合非平稳信号的分析。

  固有时间尺度分解算法将原始信号分解为一系列旋转信号分量与一个基线信号分量，通过对每层信号分量暂态信息的计算，得到原始信号精确的时频信息。其过程可描述为对于实信号 ，定义低频基线信号提取算子L与旋转分量提取算子H，使

其中，是一个基线信号，代表信号中的低频部分，为旋转信号分量，代表信号中的高频部分。用表示实信号的极值点对应的坐标， 并设 。若在某些区间为常数，选择区间的右端点作为极值点。为了便于表示，用 和 分别表示极值点 和  。假设 和 在 有定义，且 在 有定义。在相邻的极值区间 上可以定义基线信号为

其中,

  ，通常取 。在 进行信号分解，设定基线信号的初值 。信号分解为基线信号与旋转信号后，可将基线信号作为给定信号继续分解，直到所得基线信号为单调信号或者达到预设的最大分解层数。该过程可表示为​​​​​​​

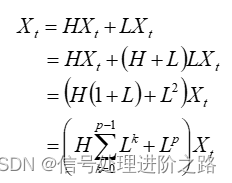
        信号共进行了p层分解，其中 为第K+1层的旋转分量，为基线信号。 

function [H,L]=Itd4(x,n,err)
% 将信号x进行ITD分解
% n分解层数
% err
%--------------------------
if nargin==1
    n=20;
    err=0.05;
end
if nargin==2
    err=0.05;
end
[tempH1,tempL]= ItdBaseDecomp4(x);
H=[tempH1];
for i=1:n-1
    [tempH,tempL]= ItdBaseDecomp4(tempL);
    H=[H;tempH];
    %----终止条件
    if dandiao(tempL)==1 %单调
        break;
    end
    if max(tempL)<err && abs(min(tempL))<err
        break;
    end
end
L=tempL;
end
function rlt=dandiao(xx)
% 求是否单调函数
x1=diff(xx);
rlt=0;
if all(x1>=0) || all(x1<=0)
    rlt=1;
end
end

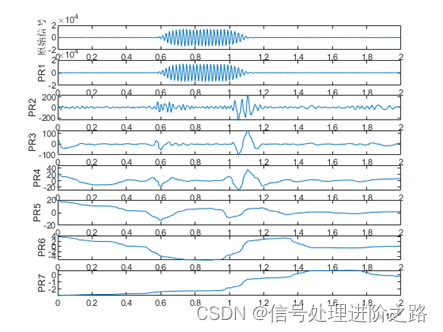
图1 信号ITD分解结果