【C++ leetcode】双指针问题（续）

3. 202 .快乐数

题目

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

• 对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
• 然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
• 如果这个过程 结果为 1，那么这个数就是快乐数。

题目链接

. - 力扣（LeetCode）

画图 和 文字 分析

对于 n ，只有两种情况，一种是 最后等于 1（即它是快乐数），一种是永远不会等于 1 (即它不是快乐数)，我们再去深入探究一下第二种情况，因为 int 类型的数据 最大有限，所以在每一次替换的过程中，得到的新的数是最后一定会回到之前出现过的数，从而陷入循环

举例：2

实际上，如果把这个当作一个链表，可以很容易区分快乐数和非快乐数，因为两种情况都有一部分是循环的，如果是快乐数，那么循环链表里面存储的都是1，如果不是快乐数，那么循环链表里面存储的不是1

这样就容易想到一种解决思路，利用快慢指针的思想

我们定义两个指针，slow 和 fast 都存储最开始的数据，slow 走一次替换， fast 走两次替换，当 slow == fast 时，它们处于循环链表里面，判断是否数据为1即可

代码

class Solution {
public:
    void is_one(int x,int &k,int &n)
    {
        while(x--)
        {
            while(n)
           {
            k += (n % 10) * (n % 10);
            n /= 10;
           }
           n = k;
           k = 0;
        }
    }
    bool isHappy(int n) 
    {
        int k = 0;
        int slow = n;
        int fast = n;
        while(1)
        {
            is_one(2,k,fast);
            is_one(1,k,slow);
            if(slow == fast)
            {
                if(slow == 1)
                {
                    return true;
                }
                else
                {
                    return false;
                }
            }
        }
 
    }
};

4. 11.盛最多量的水

题目

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

题目链接 

. - 力扣（LeetCode）

画图 和 文字 分析

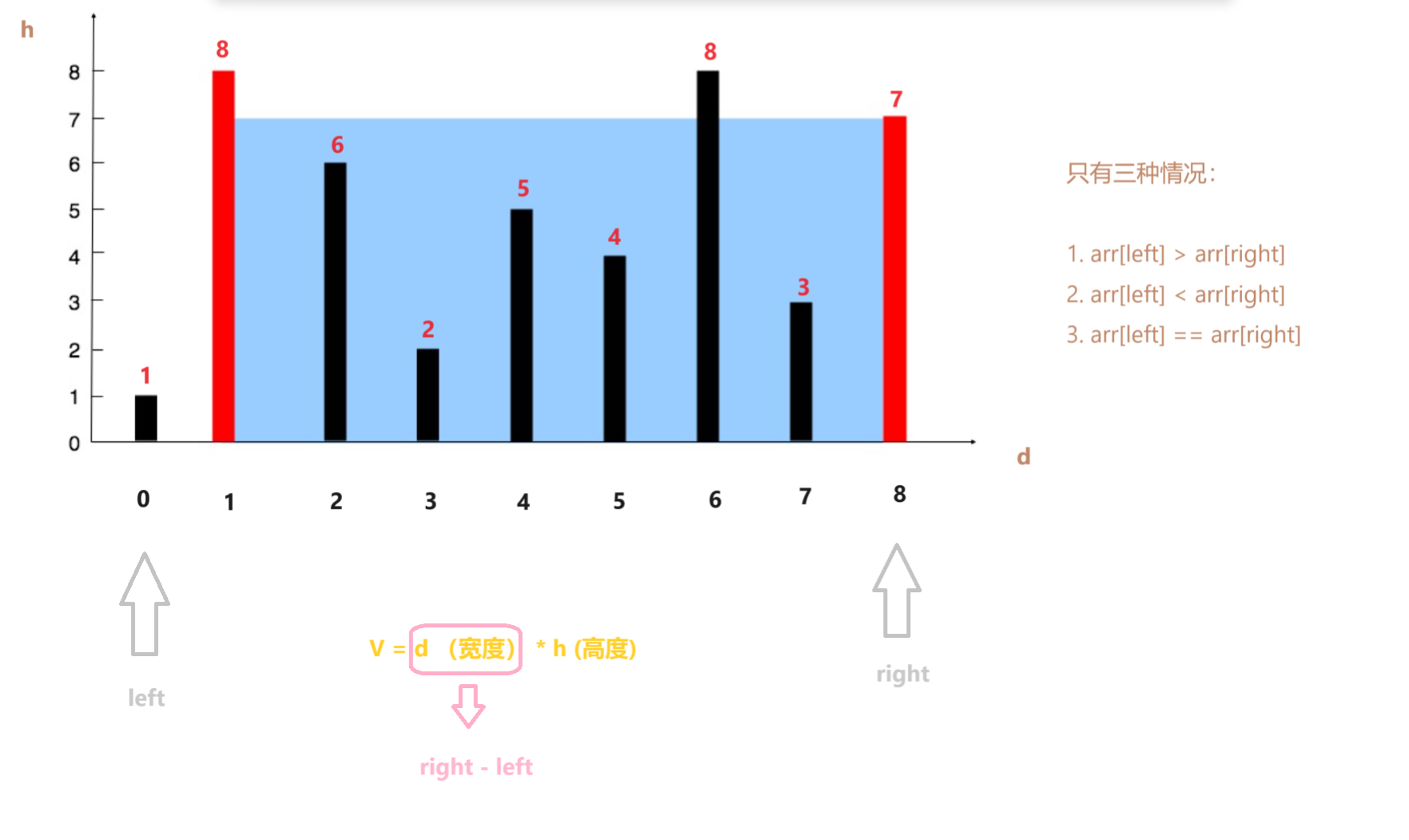
这里利用双指针的思想，定义两个指针，一个指针指向下标为 0 的位置，一个指向数组的最后一个元素的位置

V = d （宽度） * h (高度)

先记录第一次V1（即刚开始两个指针在两端点时得到的体积）

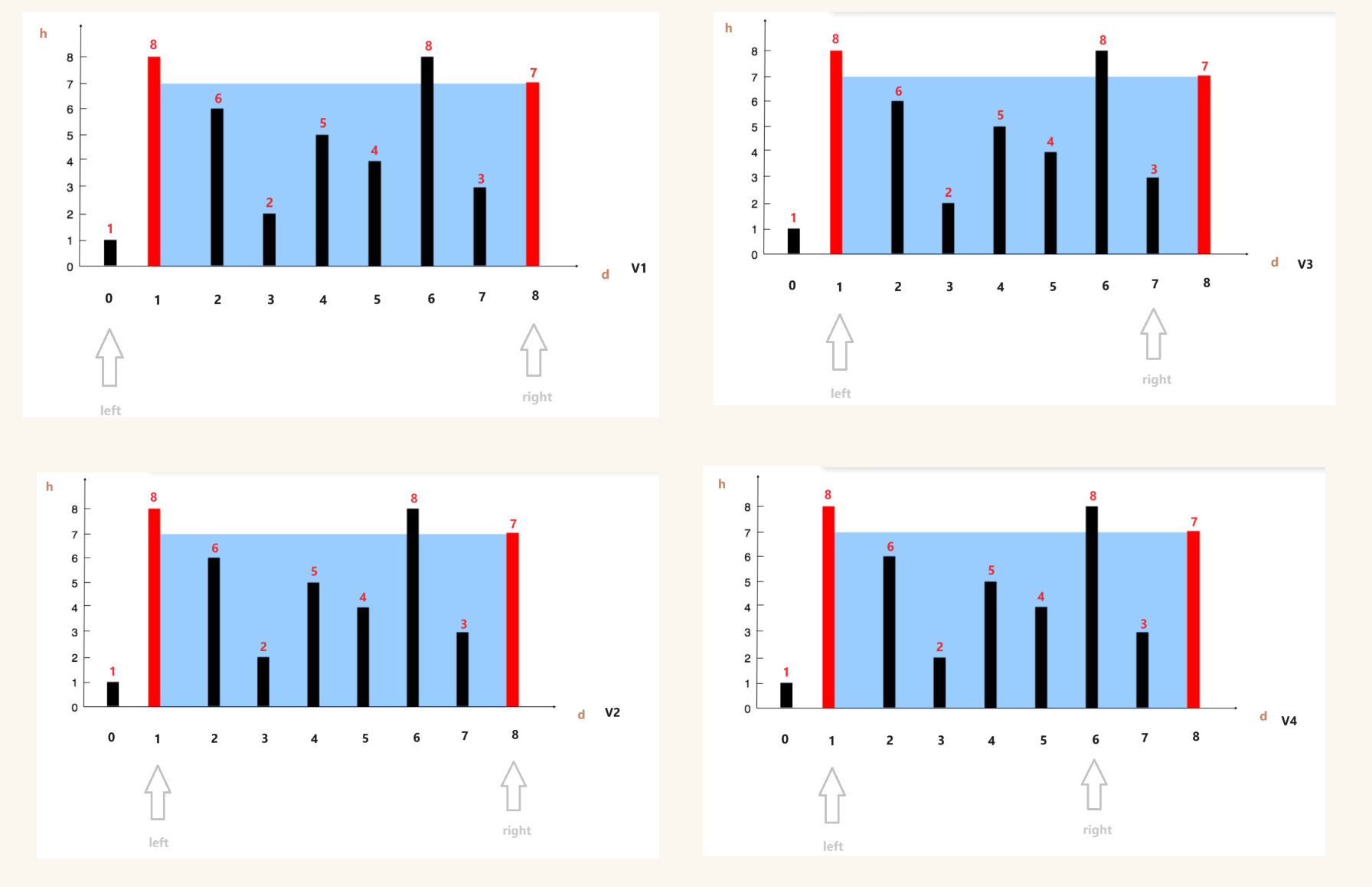
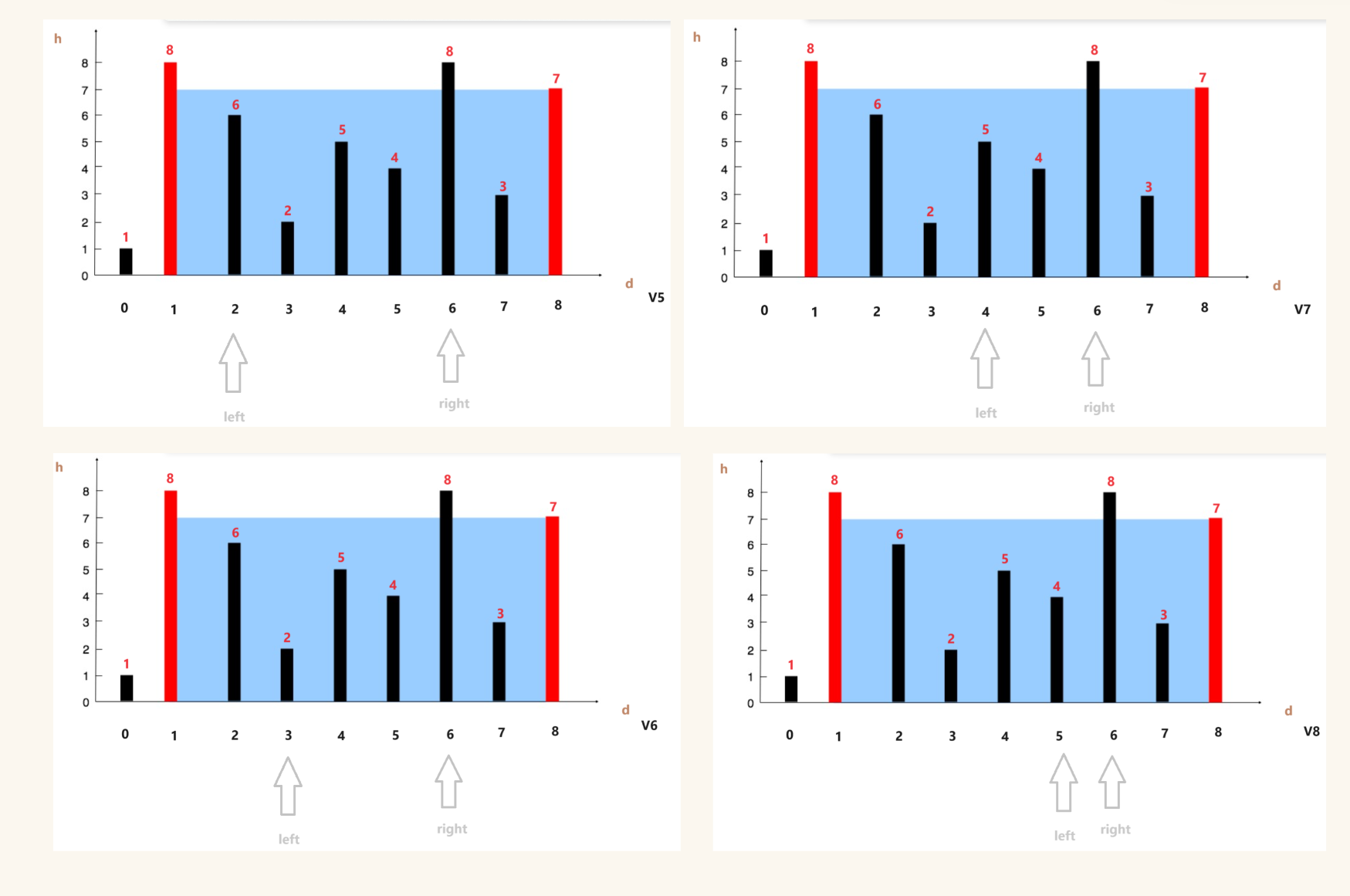
如图：对于第一种情况，right--（两个指针向里移动，d在减小，只有h变大，V才可能变大），得到的V2与V1进行对比

对于第二种情况，left++,得到结果再进行对比

对于第三章情况，可以把它归到第一种情况或者第二种情况

注意：

第三种情况不可以不做处理，因为两指针向里运动时，还可能得到更大的V

举例：输入：[1,8,6,2,5,4,8,3,7] ，输出 ：49

 代码

class Solution {
public:
    int maxArea(vector<int>& height)
    {
        int v = 0;
        int i = 0;
        int j = height.size() - 1;
        int min = height[i] < height[j] ? height[i] : height[j];
        v = (j - i) * min > v ?  (j - i) * min : v;
        while (i < j)
        {
            if (height[i] > height[j])
            {
                j--;
                min = height[i] < height[j] ? height[i] : height[j];
                v = (j - i) * min > v ?  (j - i) * min : v;
            }
            else
            {
                i++;
                min = height[i] < height[j] ? height[i] : height[j];
                 v = (j - i) * min > v ?  (j - i) * min : v;
            }
            
        }
       
        return v;
    }
};