热门标签
热门文章
- 1mac终端下使用sed命令,报错“command a expects \ followed by text”
- 2linux sed的详细讲解与使用方法_linux sed -i替换
- 3blender渲染代码_blender后台渲染调用源码
- 4blender多张图层渲染结果保存导出到设定文件夹_blender分层导出
- 5【愚公系列】2022年09月 微信小程序-图片懒加载功能实现_在uniapp中使用npm install --save mina-lazy-image
- 6tensorRT的使用笔记!_tensorrt 输入输出
- 7vivado 仿真_QuestaSim/Modelsim用脚本自动化仿真Quartus II IP Core
- 8机器学习笔记(3)—多变量线性回归
- 9荣耀X40,X30,X20,X10,荣耀70,荣耀60 安装谷歌套件谷歌服务框架GMS,Google Play商店_荣耀x40谷歌框架安装
- 10vue3如何二次封装el-upload组件进行图片上传及删除
当前位置: article > 正文
java-边界线查找-离散点最小(凸)包围边界查找_java 将最外围的点连接起来
作者:Gausst松鼠会 | 2024-03-29 02:29:16
赞
踩
java 将最外围的点连接起来
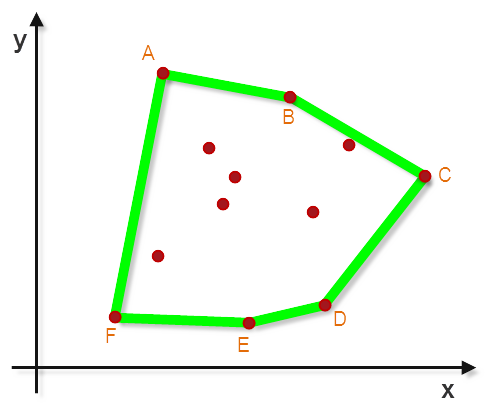
就是一堆散点,需要把最外侧点链接起来成为一个多边形
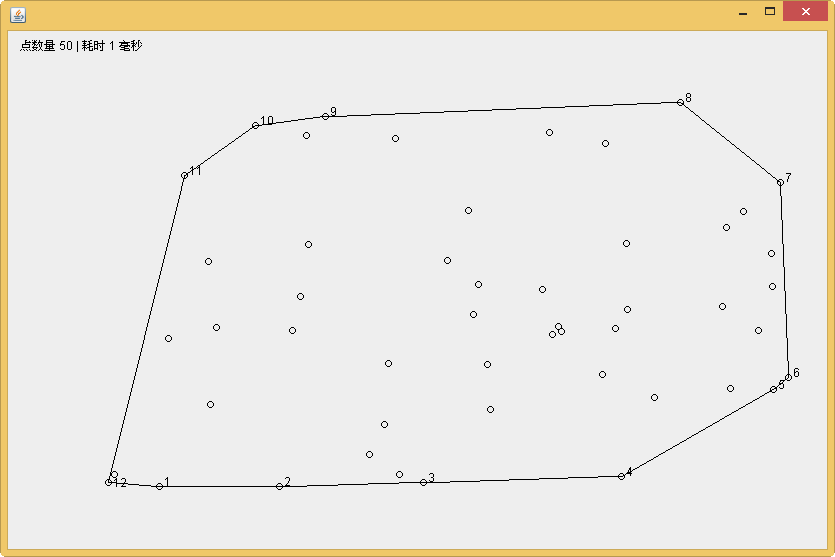
先看效果图:有很多无序的点,把最外侧点链接起来成为一个多边形
最近,项目中有一需求,需要用一条闭合曲线将离散坐标点勾勒出来
根据Darel Rex Finley的程序,其实现了最小凸多边形边界查找(关于凸多边形及凹多边形的定义见 凸多边形 及 凹多边形)
以下介绍java版的实现过程
离散点
首先建立离散点类:
- /**
- * <p>
- * <b>离散点</b>
- * <p>
- * <pre>
- * 离散点
- * </pre>
- *
- * @author ManerFan 2015年4月10日
- */
- public class Point {
-
- /**
- * x坐标
- */
- private double x;
-
- /**
- * y坐标
- */
- private double y;
-
- /**
- * 边界查找算法中 是否被找到
- */
- boolean founded = false;
-
- public Point() {
- }
-
- public Point(double x, double y) {
- this.x = x;
- this.y = y;
- }
-
- public double getX() {
- return x;
- }
-
- public void setX(double x) {
- this.x = x;
- }
-
- public double getY() {
- return y;
- }
-
- public void setY(double y) {
- this.y = y;
- }
-
- @Override
- public String toString() {
- return "(" + x + ", " + y + ")";
- }
-
- @Override
- public int hashCode() {
- final int prime = 31;
- int result = 1;
- long temp;
- temp = Double.doubleToLongBits(x);
- result = prime * result + (int) (temp ^ (temp >>> 32));
- temp = Double.doubleToLongBits(y);
- result = prime * result + (int) (temp ^ (temp >>> 32));
- return result;
- }
-
- @Override
- public boolean equals(Object obj) {
- if (this == obj)
- return true;
- if (obj == null)
- return false;
- if (getClass() != obj.getClass())
- return false;
- Point other = (Point) obj;
- if (Double.doubleToLongBits(x) != Double.doubleToLongBits(other.x))
- return false;
- if (Double.doubleToLongBits(y) != Double.doubleToLongBits(other.y))
- return false;
- return true;
- }
-
- }
离散点操作工具类
为更方便的实现算法,创建离散点操作工具类:
- /**
- * <p>
- * <b>离散点计算工具</b>
- * <p>
- * <pre>
- * 离散点计算工具
- *
- * y
- * ↑ · ·
- * │ · · ·
- * │ · · · ·
- * │ · ·
- * —│————————————→ x
- * </pre>
- *
- * @author ManerFan 2015年4月9日
- */
- public class DiscretePointUtil {
-
- /**
- * <p>
- * <b>查找离散点集中的(min_x, min_Y) (max_x, max_Y)</b>
- * <p>
- * <pre>
- * 查找离散点集中的(min_x, min_Y) (max_x, max_Y)
- * </pre>
- *
- * @author ManerFan 2015年4月9日
- * @param points 离散点集
- * @return [(min_x, min_Y), (max_x, max_Y)]
- */
- public static Point[] calMinMaxDots(final List<Point> points) {
- if (null == points || points.isEmpty()) {
- return null;
- }
-
- double min_x = points.get(0).getX(), max_x = points.get(0).getX();
- double min_y = points.get(0).getY(), max_y = points.get(0).getY();
-
- /* 这里存在优化空间,可以使用并行计算 */
- for (Point point : points) {
- if (min_x > point.getX()) {
- min_x = point.getX();
- }
-
- if (max_x < point.getX()) {
- max_x = point.getX();
- }
-
- if (min_y > point.getY()) {
- min_y = point.getY();
- }
-
- if (max_y < point.getY()) {
- max_y = point.getY();
- }
- }
-
- Point ws = new Point(min_x, min_y);
- Point en = new Point(max_x, max_y);
-
- return new Point[] { ws, en };
- }
-
- /**
- * <p>
- * <b>求矩形面积平方根</b>
- * <p>
- * <pre>
- * 以两个点作为矩形的对角线上的两点,计算其面积的平方根
- * </pre>
- *
- * @author ManerFan 2015年4月9日
- * @param ws 西南点
- * @param en 东北点
- * @return 矩形面积平方根
- */
- public static double calRectAreaSquare(Point ws, Point en) {
- if (null == ws || null == en) {
- return .0;
- }
-
- /* 为防止计算面积时float溢出,先计算各边平方根,再相乘 */
- return Math.sqrt(Math.abs(ws.getX() - en.getX()))
- * Math.sqrt(Math.abs(ws.getY() - en.getY()));
- }
-
- /**
- * <p>
- * <b>求两点之间的长度</b>
- * <p>
- * <pre>
- * 求两点之间的长度
- * </pre>
- *
- * @author ManerFan 2015年4月10日
- * @param ws 西南点
- * @param en 东北点
- * @return 两点之间的长度
- */
- public static double calLineLen(Point ws, Point en) {
- if (null == ws || null == en) {
- return .0;
- }
-
- if (ws.equals(en)) {
- return .0;
- }
-
- double a = Math.abs(ws.getX() - en.getX()); // 直角三角形的直边a
- double b = Math.abs(ws.getY() - en.getY()); // 直角三角形的直边b
-
- double min = Math.min(a, b); // 短直边
- double max = Math.max(a, b); // 长直边
-
- /**
- * 为防止计算平方时float溢出,做如下转换
- * √(min²+max²) = √((min/max)²+1) * abs(max)
- */
- double inner = min / max;
- return Math.sqrt(inner * inner + 1.0) * max;
- }
-
- /**
- * <p>
- * <b>求两点间的中心点</b>
- * <p>
- * <pre>
- * 求两点间的中心点
- * </pre>
- *
- * @author ManerFan 2015年4月10日
- * @param ws 西南点
- * @param en 东北点
- * @return 两点间的中心点
- */
- public static Point calCerter(Point ws, Point en) {
- if (null == ws || null == en) {
- return null;
- }
-
- return new Point(ws.getX() + (en.getX() - ws.getX()) / 2.0, ws.getY()
- + (en.getY() - ws.getY()) / 2.0);
- }
-
- /**
- * <p>
- * <b>计算向量角</b>
- * <p>
- * <pre>
- * 计算两点组成的向量与x轴正方向的向量角
- * </pre>
- *
- * @author ManerFan 2015年4月17日
- * @param s 向量起点
- * @param d 向量终点
- * @return 向量角
- */
- public static double angleOf(Point s, Point d) {
- double dist = calLineLen(s, d);
-
- if (dist <= 0) {
- return .0;
- }
-
- double x = d.getX() - s.getX(); // 直角三角形的直边a
- double y = d.getY() - s.getY(); // 直角三角形的直边b
-
- if (y >= 0.) { /* 1 2 象限 */
- return Math.acos(x / dist);
- } else { /* 3 4 象限 */
- return Math.acos(-x / dist) + Math.PI;
- }
- }
-
- /**
- * <p>
- * <b>修正角度</b>
- * <p>
- * <pre>
- * 修正角度到 [0, 2PI]
- * </pre>
- *
- * @author ManerFan 2015年4月17日
- * @param angle 原始角度
- * @return 修正后的角度
- */
- public static double reviseAngle(double angle) {
- while (angle < 0.) {
- angle += 2 * Math.PI;
- }
- while (angle >= 2 * Math.PI) {
- angle -= 2 * Math.PI;
- }
-
- return angle;
- }
-
- }
边界查找算法
算法的实现思路,简要如下
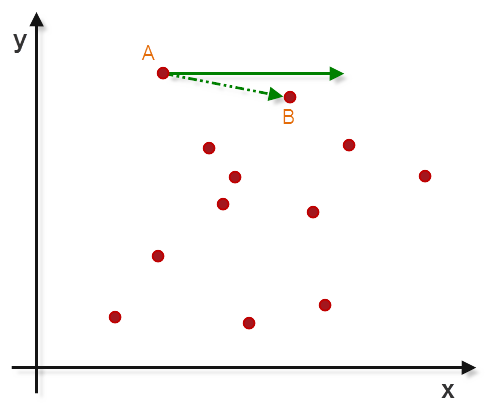
找到离散点中,保证y坐标最大的情况下,x坐标最小的点,记做A点
以A点为原点,x轴正反向射线(Ax−→Ax→)顺时针扫描,找到旋转角最小时扫描到的点,记做B点
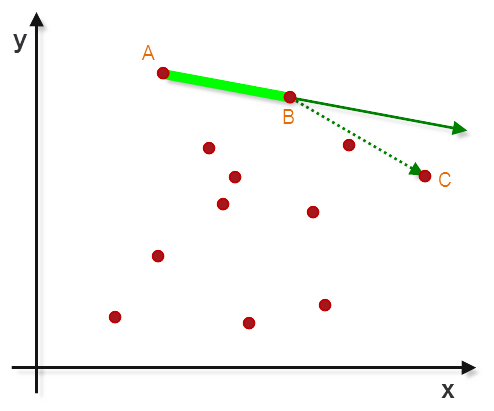
以B点为原点,AB方向射线(AB−→−AB→)顺时针扫描,找到旋转角最小时扫描到的点,记做C点
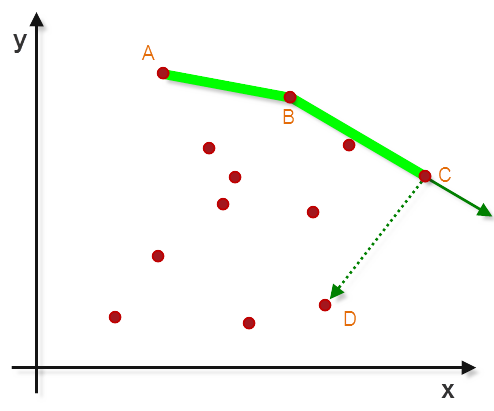
以C点为原点,BC方向射线(BC−→−BC→)顺时针扫描,找到旋转角最小时扫描到的点,记做D点
以此类推,直到找到起始点A
思路图,简要如下
实现程序见下:
- /**
- * <p>
- * <b>最小(凸)包围边界查找</b>
- * <p>
- * <pre>
- * 最小(凸)包围边界查找
- *
- * Minimum Bounding Polygon (Convex Hull; Smallest Enclosing A Set of Points)
- * <b><a href="http://alienryderflex.com/smallest_enclosing_polygon/">©2009 Darel Rex Finley.</a></b>
- *
- * y
- * ↑ · ·
- * │ · · ·
- * │ · · · ·
- * │ · ·
- * —│————————————→ x
- *
- * </pre>
- *
- * @author ManerFan 2015年4月17日
- */
- public class MinimumBoundingPolygon {
-
- public static LinkedList<Point> findSmallestPolygon(List<Point> ps) {
- if (null == ps || ps.isEmpty()) {
- return null;
- }
-
- Point corner = findStartPoint(ps);
- if (null == corner) {
- return null;
- }
-
- double minAngleDif, oldAngle = 2 * Math.PI;
- LinkedList<Point> bound = new LinkedList<>();
- do {
- minAngleDif = 2 * Math.PI;
-
- bound.add(corner);
-
- Point nextPoint = corner;
- double nextAngle = oldAngle;
- for (Point p : ps) {
- if (p.founded) { // 已被加入边界链表的点
- continue;
- }
-
- if (p.equals(corner)) { // 重合点
- /*if (!p.equals(bound.getFirst())) {
- p.founded = true;
- }*/
- continue;
- }
-
- double currAngle = DiscretePointUtil.angleOf(corner, p); /* 当前向量与x轴正方向的夹角 */
- double angleDif = DiscretePointUtil.reviseAngle(oldAngle - currAngle); /* 两条向量之间的夹角(顺时针旋转的夹角) */
-
- if (angleDif < minAngleDif) {
- minAngleDif = angleDif;
- nextPoint = p;
- nextAngle = currAngle;
- }
- }
-
- oldAngle = nextAngle;
- corner = nextPoint;
- corner.founded = true;
- } while (!corner.equals(bound.getFirst())); /* 判断边界是否闭合 */
-
- return bound;
- }
-
- /** 查找起始点(保证y最大的情况下、尽量使x最小的点) */
- private static Point findStartPoint(List<Point> ps) {
- if (null == ps || ps.isEmpty()) {
- return null;
- }
-
- Point p = ps.get(0);
- ListIterator<Point> iter = ps.listIterator();
-
- while (iter.hasNext()) {
- Point point = iter.next();
- if (point.getY() > p.getY() || (point.getY() == p.getY() && point.getX() < p.getX())) { /* 找到最靠上靠左的点 */
- p = point;
- }
- }
-
- return p;
- }
- }
结合上边的几张图,相比不难看懂
以下附上一张实际效果图:
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/Gausst松鼠会/article/detail/333177
推荐阅读
相关标签