- 1面试官:你知道Redis的热key问题吗?给出几个解决方案,详细点?_redis热key解决方案
- 2Spatial-Temporal Transformer Networks for Traffic Flow Forecasting
- 3图像哈希:全局+局部提取特征
- 4模拟电路设计(24)---几种不同类型的A/D转换器的转换原理_改进型双积分ad转换器设计
- 5cargo设置国内源 windows+linux_cargo 国内源
- 6C# 如何调用python,避免重复造轮子_c#调用python函数
- 7详解PostgreSQL聚合函数: 精准统计数据,提升效率 附代码示例_pgsql 聚合函数
- 8数字电路思考题汇总_试用j-k触发器构成一个模8格雷码同步计数器(画出逻辑图)。
- 9深入理解Stable Diffusion:技术原理与实战应用_分析stable diffusion是否满足收敛性的条件
- 10基于百度文心大模型全面重构,小度正式推出AI原生操作系统DuerOS X
SPSS常用的10种统计分析_spss数据分析
赞
踩
目录
实验一 地理数据的统计处理
一、实验目的
了解地理数据分布的基本特征,掌握地理数据分布特征的主要表征值。重点掌握SPSS统计处理中的主要参数设置及其含义,并分析检验结果。
二、实验数据

三、实验内容
运用SPSS应用软件中的描述和频数模块,重点掌握标准差、最大值、最小值、方差、全距、算术平均数、众数、中位数、算数和以及偏态、峰度的计算等。
四、实验步骤
(1)在Excel表中将数据转置,再将数据导入到SPSS中。
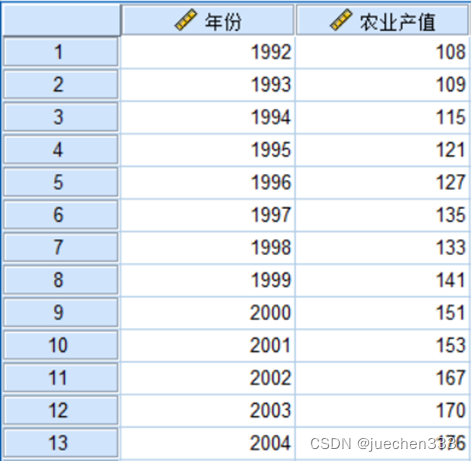
(2)打开【描述统计】|【描述】,将农业产值添加到【变量中】。

(3)在【选项】中勾选【标准差】、【最小值】、【最大值】、【方差】、【范围】、【标准误差平均值】、【峰度】和【偏度】。
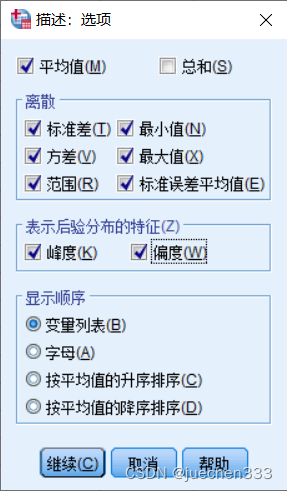
(4)结果

实验二 双变量相关分析
一、实验目的
掌握相关分析的定义、内涵,重点掌握一般相关系数的计算公式。
二、实验数据
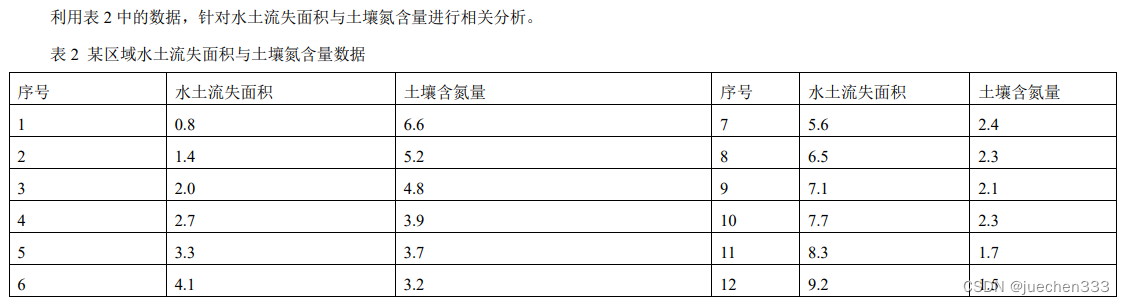
三、实验内容
运用SPSS应用软件中的Correlate模块进行两两要素间的相关分析,并能够进行检验,利用所给数据进行预测。
四、实验步骤
(1)将Excel表数据导入到SPSS中。

(2)打开【分析】|【相关】|【双变量】,将水土流失面积和土壤含氮量添加到【变量】中。
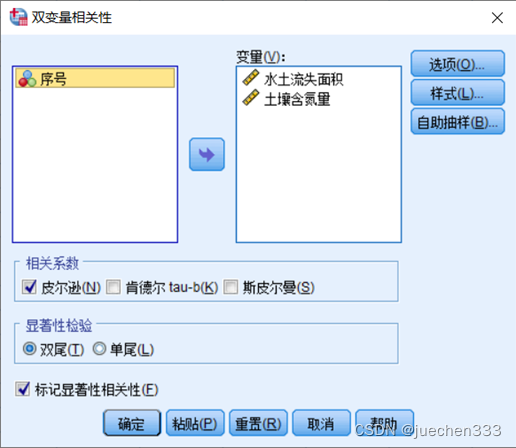
(3)结果
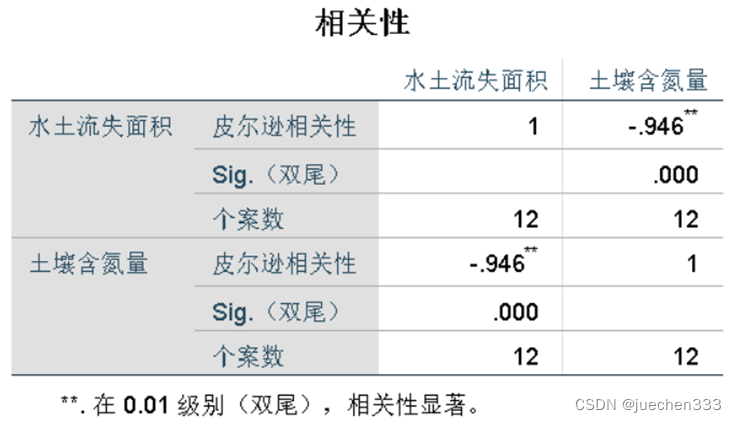
从图中我们可以得到相关系数为-0.946,呈现负相关,右上角有**,说明相关性显著,通过了相关性检验。
实验三 主成分分析
一、实验目的
掌握SPSS软件进行主成分分析的功能,掌握主成分分析的基本思想和操作过程并对得到的结果进行分析并给出统计解释。
二、实验数据


三、实验内容
利用中国主要城市影响经济发展的主要指标数据,运用主成分分析方法进行分析。
四、实验步骤
(1)将Excel表数据导入到SPSS中。

(2)打开【分析】|【降维】|【因子分析】工具,将数据中除了【城市】的其他10个变量全部添加进去。
(3)点击【描述】,勾选【初始解】、【系数】、【KMO和巴特利特球形度检验】选项
(4)点击【抽取】,勾选【碎石图】选项
(5)结果

KMO的值为0.762,大于0.7,较为适合做主成分分析

变量的方差能被主成分解释在80%—90%以上


可知前两个成分的累计贡献率已经达到85%,所以将前两个成分作为主成分;从碎石图也可以看出,第一成分和第二成分贡献了大部分信息。

(6)因为相关系数矩阵的特征根=方差贡献=主成分得分的方差,所以在Excel中通过SUMSQ函数可以计算得到第一主成分和第二主成分的特征值分别为6.263和2.350。

(7)将主成分矩阵复制到SPSS中

(8)打开【转换】|【计算变量】工具,输入公式:V1(第一主成分的载荷值)/SQRT(6.263(第一主成分的特征值)),对于第二主成分计算其特征向量进行相同的操作


两个主成分的表达式为:
Y1=0.28X1+0.06X2+0.24X3+0.34X4+0.19X5+0.38X6+0.36X7+0.38X8+0.38X9+0.38X10
Y2=0.42X1-0.55X2+0.44X3-0.21X4+0.44X5-0.03X6-0.22X7-0.12X8-0.01X9-0.17X10
实验四 因子分析
一、实验目的
使用SPSS软件进行因子分析,掌握因子分析的原理和方法。
二、实验数据
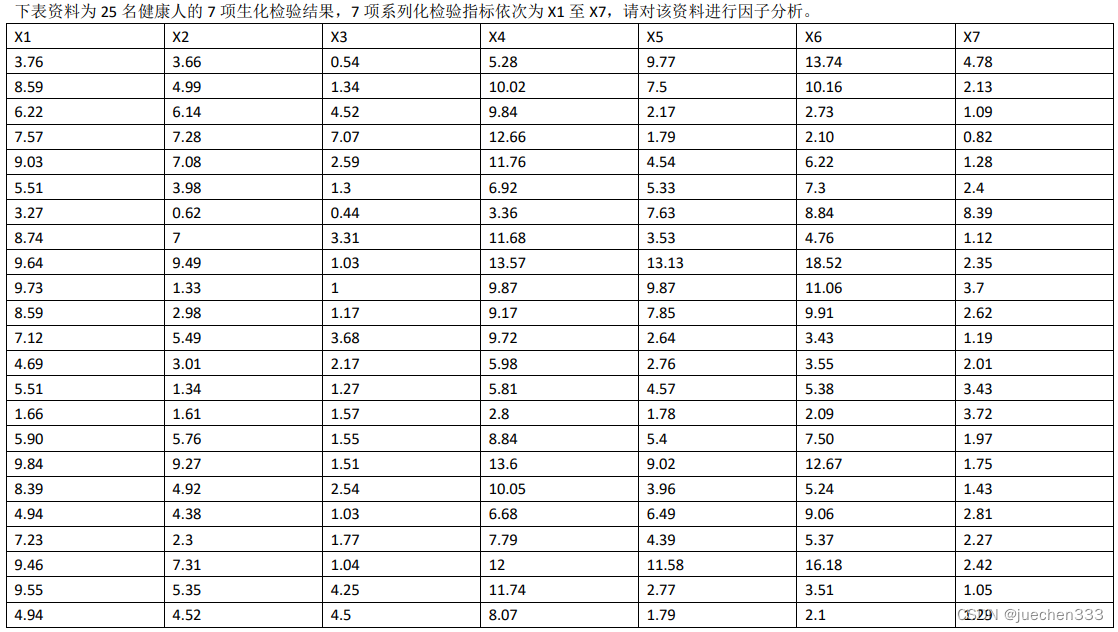
![]()
三、实验内容
利用25名健康人的7项生化检验结果资料,7项系列化检验指标依次为X1至X7,对该资料进行因子分析。
四、实验步骤
(1)将Excel数据导入到SPSS中。

(2)打开【分析】|【降维】|【因子分析】工具,将变量全部添加进去
(3)勾选【描述】中的【系数】和【KMO和巴特利球形度检验】

(4)勾选【旋转】中的【最大方差法】

(5)勾选【选项】中的【按大小排序】和【取消小系数】
(6)结果



旋转后的成分矩阵:

实验五 多元线性回归
一、实验目的
掌握多元回归模型的建立方法、步骤、检验的过程等。
二、实验数据

三、实验内容
利用数据分析降水量和蒸发量对径流深的影响,进行多元线性回归分析。
四、实验步骤
(1)将Excel数据导入到SPSS中

(2)打开【分析】|【回归】|【线性】工具,将 径流深度 添加到【因变量】中,将 年降水量 和 年蒸发量 添加到【自变量】中

(3)在【统计】中勾选【德宾·沃森】、【部分相关性和偏相关性】和【共线性诊断】

(4)在【图】中将【*ZRESID】选入【Y】中,将【*ZPRED】选入【X】中,勾选【直方图】和【正态概率图】
(5)结果
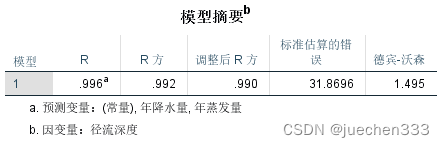
可知DW值接近于2,自变量的自相关性不明显;R方为0.992,模型拟合度非常好

显著性表示自变量对因变量的影响程度,小于0.05表示于显著影响,越小影响越大,由表可以知道年降水量和年蒸发量对径流深度有显著影响。
VIF用于共线性诊断(变量之间的关联度),当0<VIF<10时,不存在多重共线性,由表可知年降水量和年蒸发量之间不存在多重共线性。
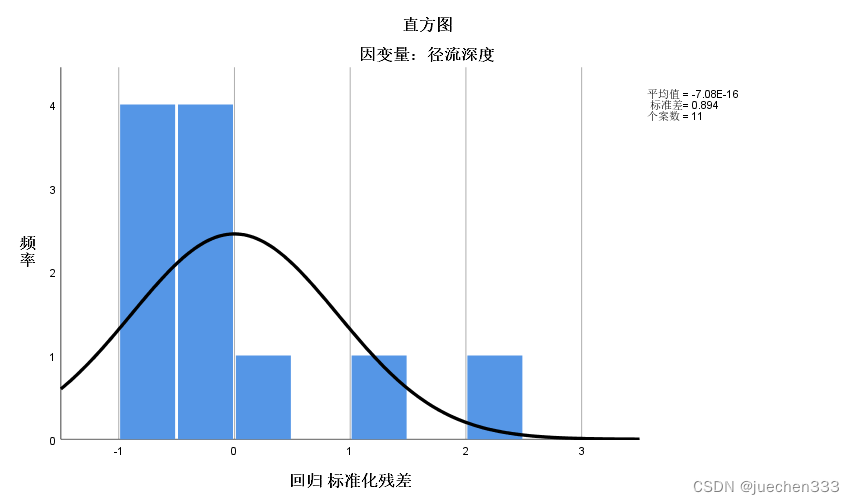
根据直方图可以知道直方图和正态曲线较为不吻合,说明残差不符合正态分布。
实验六 聚类分析
一、实验目的
通过此次实验,重点掌握样本聚类方法的概念、基本思路、数据处理的方式,并能对结果进行分析。
二、实验数据
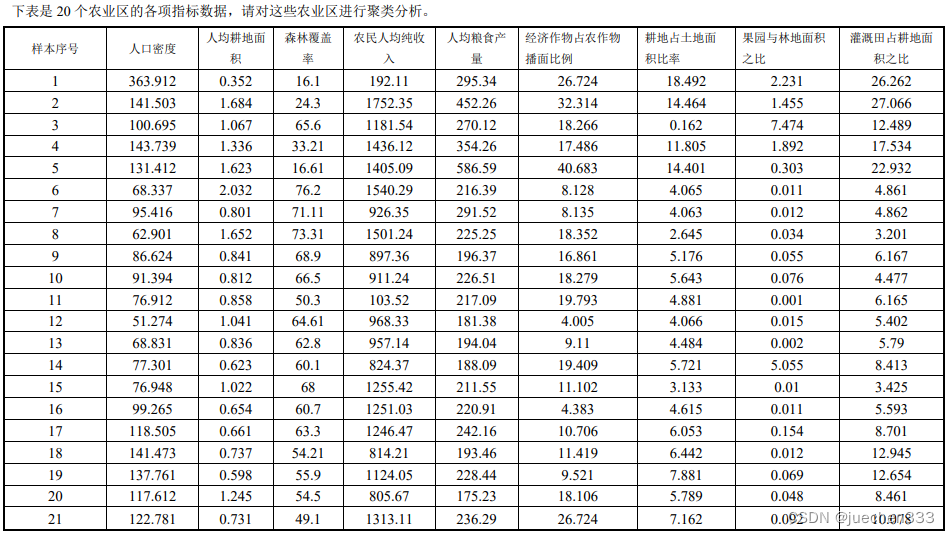
三、实验内容
运用SPSS应用软件中的系统聚类,建立分层聚类的基本概念,掌握数据标准化的方法、统计量的计算方式以及聚类的方法的选择,并根据自动生成的聚类谱系图进行类型的划分。
四、实验步骤
(1)将Excel数据导入到SPSS中。
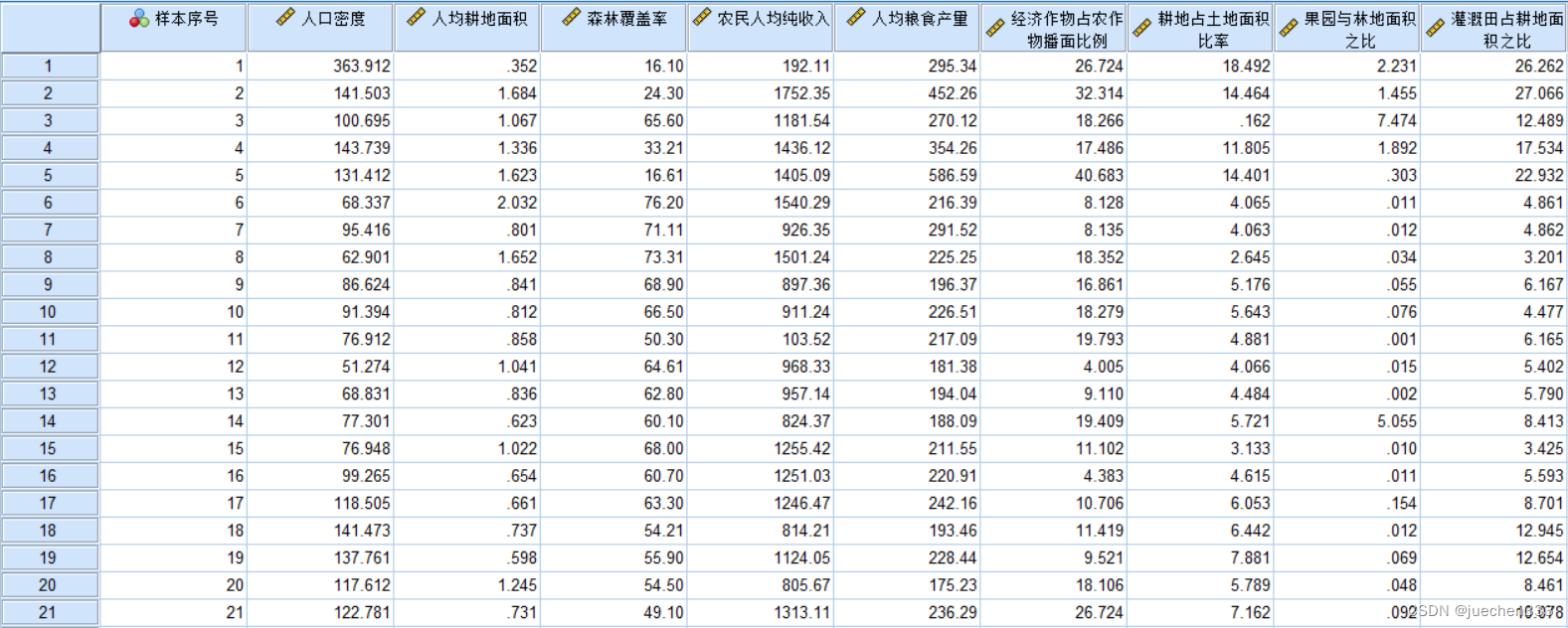
(2)打开【分析】|【分类】|【系统聚类】工具,将数据中除样本序号的所有变量全部添加进去。
(3)在【图】中勾选【谱系图】
(4)结果

没有数据缺失,故全部21个样本参与聚类,有效样品为100%
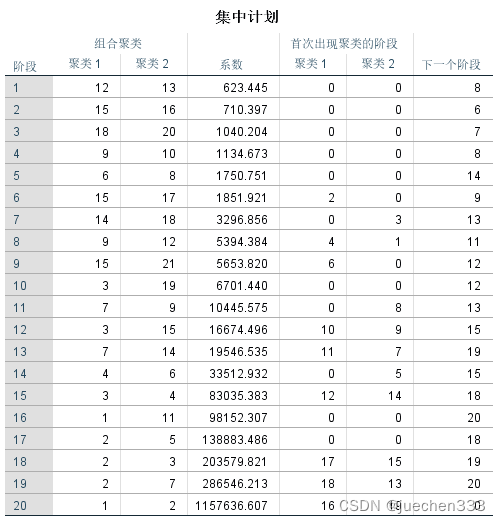
首先将第12号样品和第13号样品聚为一类,这两个样品的夹角余弦值最大。
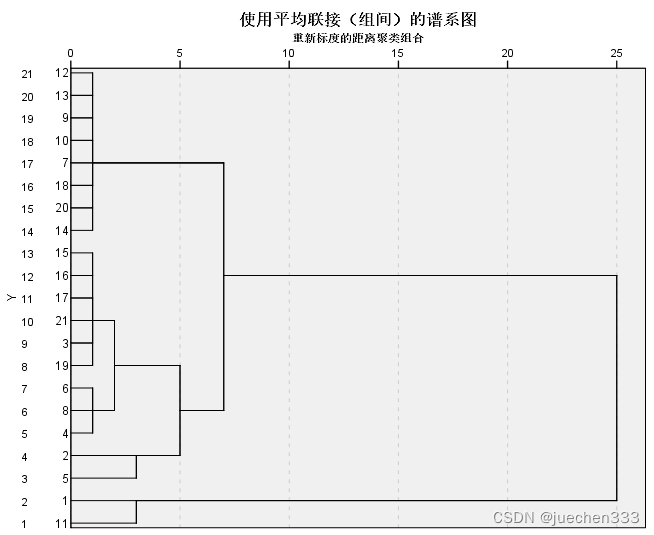
根据树形图,选择适当的尺度分为若干类。
实验七 时间序列分析
一、实验目的
掌握时间序列分析的基本方法步骤。
二、实验数据

三、实验内容
利用SPSS对某地区农业收成变化状态转移情况的数据,进行2030年的农业收成状况进行预测。
四、实验步骤
(1)将Excel数据导入到SPSS中
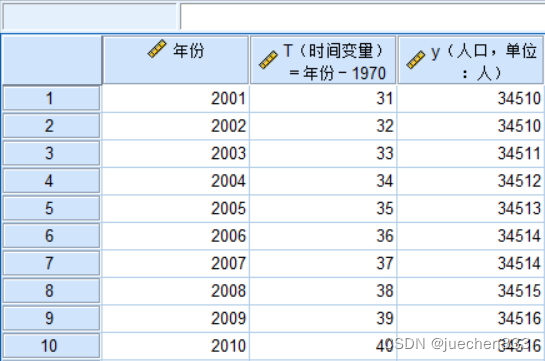
(2)打开【数据】|【定义日期和时间】,因为时间变量是从2001开始的,所以设置为2001年
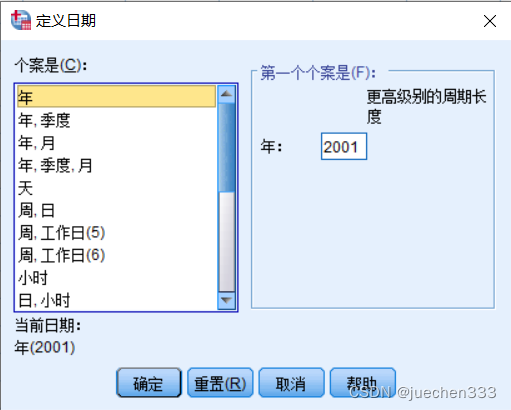
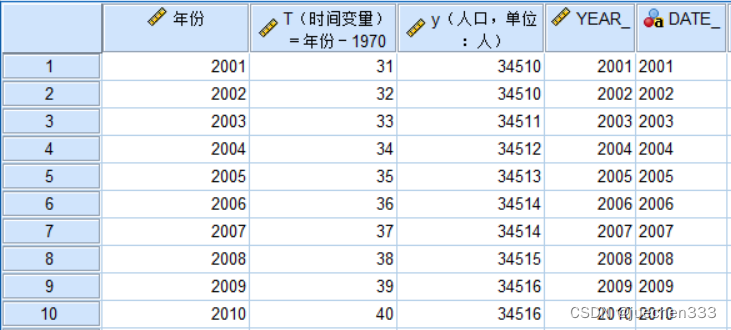
(3)打开【分析】|【时间序列预测】|【创建传统模型】,将 人口数量 导入因变量,年份导入自变量,将【方法】改为【ARIMA】。
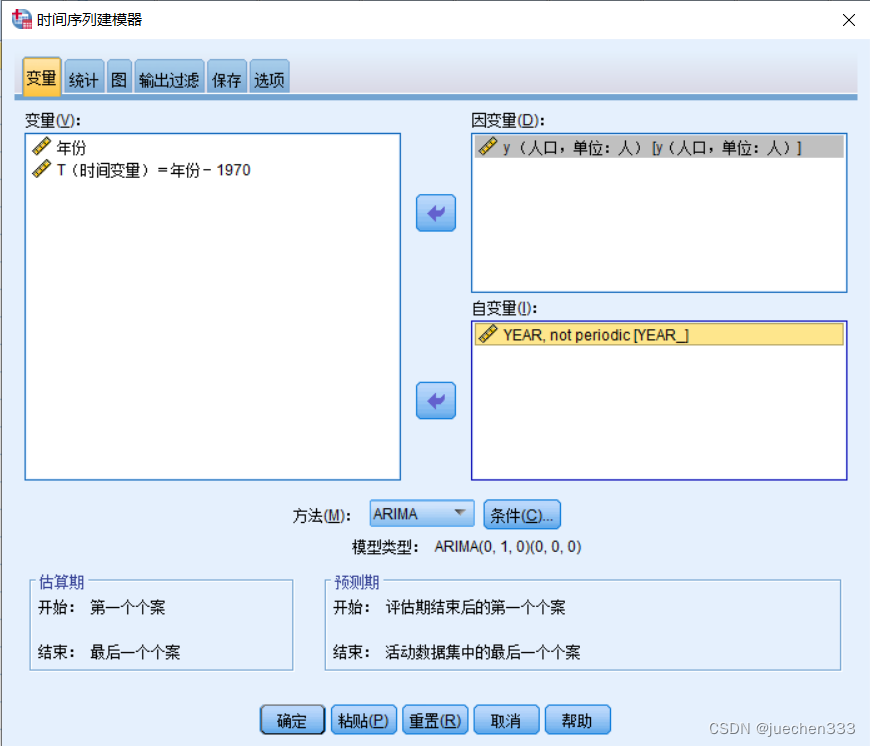
(4)在【统计】中勾选【显示预测值】
(5)在【保存】中勾选【预测值】
(6)预估到2050年

(7)结果
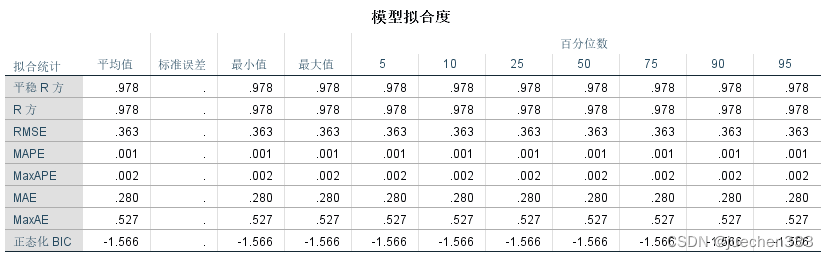
预测结果:
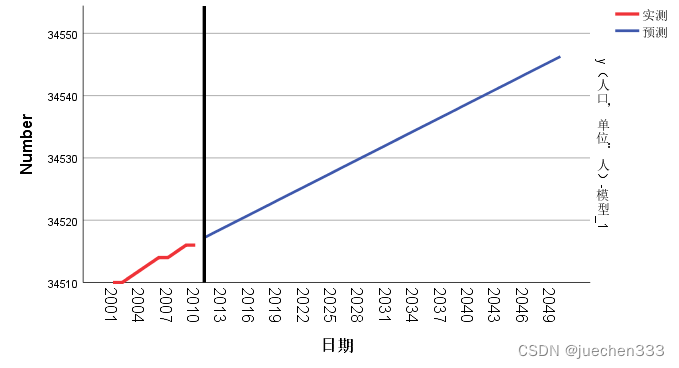
实验八 地统计分析
一、实验目的
掌握ArcGIS地统计分析功能。
二、实验数据
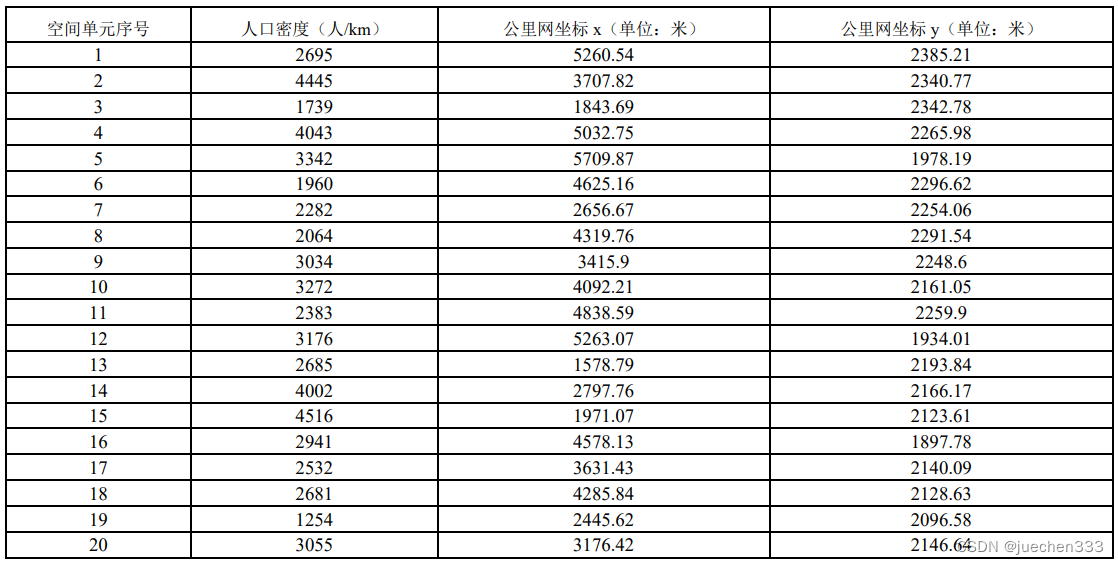


三、实验内容
根据给出的数据用半变异函数进行分析。
四、实验步骤
(1)将Excel数据导入到ArcMap中,并导出为shapefile格式
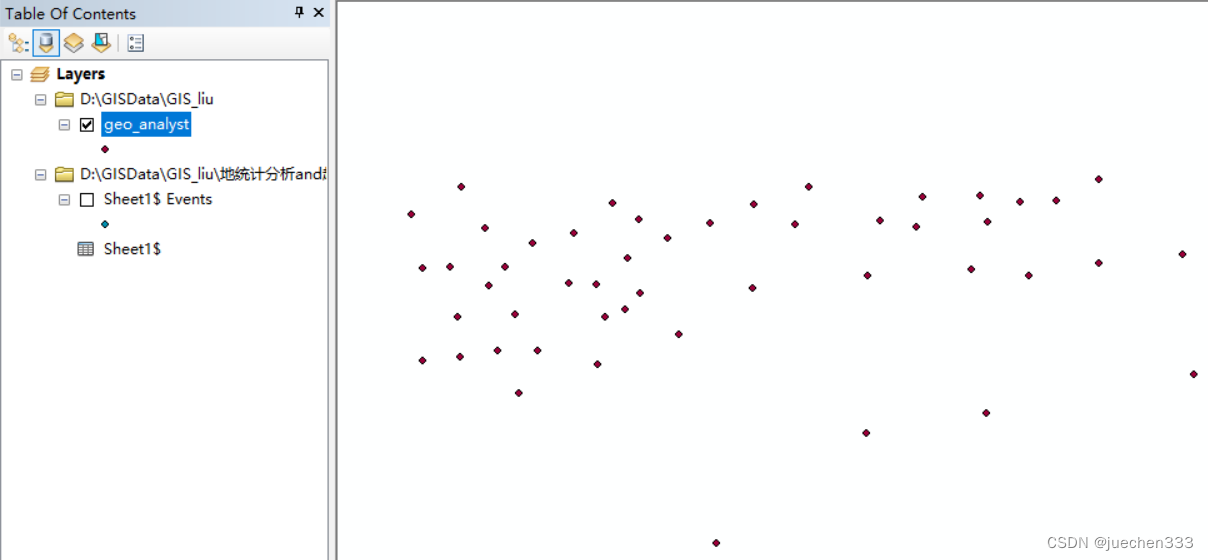
(2)打开【Geostatistical Analyst】下【Explore Data】的直方图【Histogram】,发现偏度指数Skewness偏离0较为严重,所以去掉最大的那一列数据。
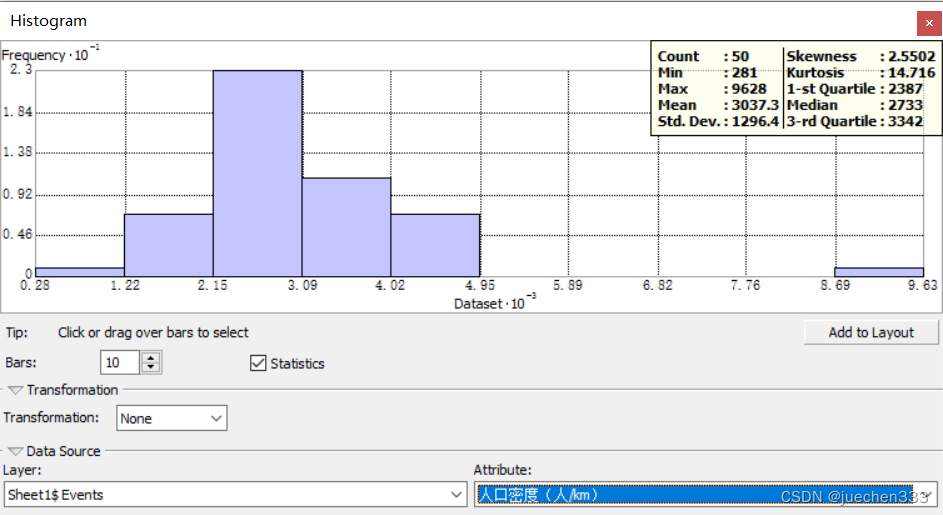
新直方图的偏移指数较为接近0,符合正态分布。
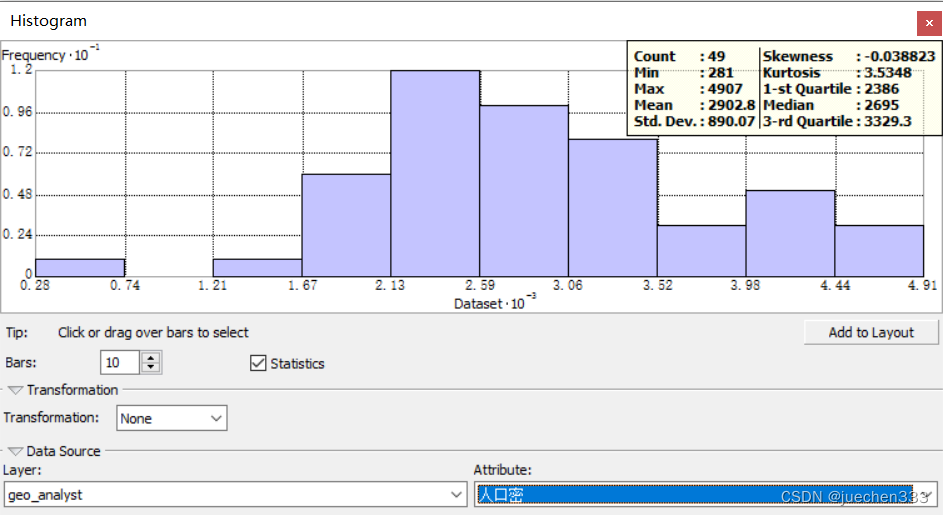
(3)使用QQ图来检验数据是否服从正态分布,打开【Geostatistical Analyst】下【Explore Data】的【Normal QQPlot】
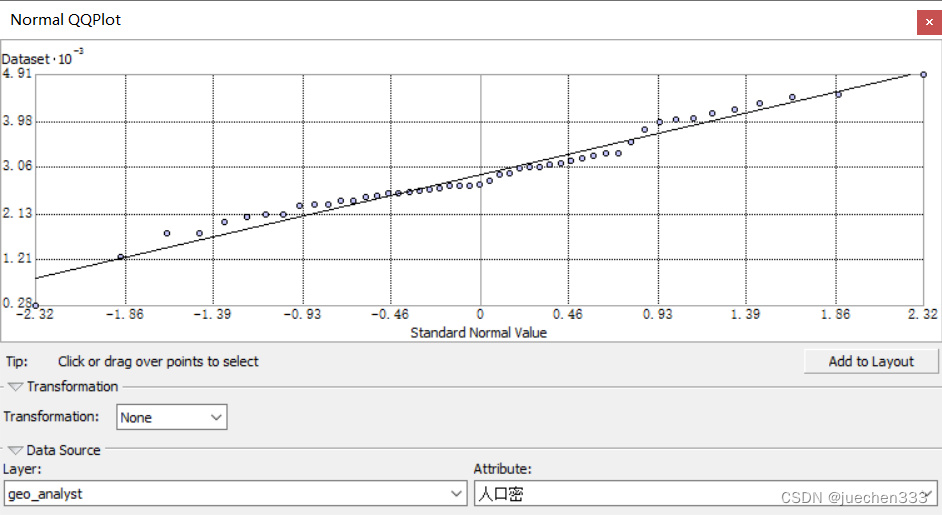
点主要分布在直线附近,说明服从正态分布。
(4)检查数据是否存在趋势分布,打开【Geostatistical Analyst】下【Explore Data】的【Trend Analysis】

从拟合曲线可以看出,在X值相对较小区域,Y值相对较大区域,人口密度较大。
(5)进行空间自相关分析,打开【Geostatistical Analyst】|【Explore Data】|【Semivariogram/Covariance Cloud】
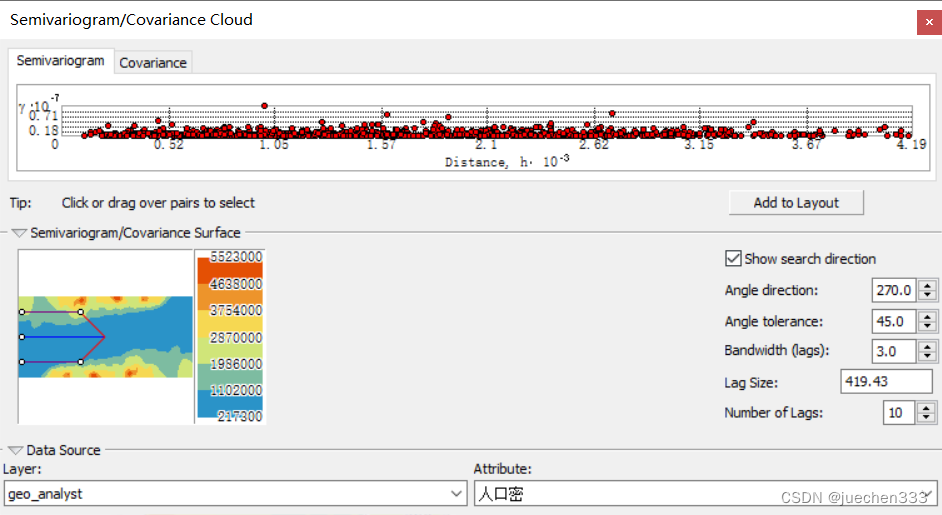
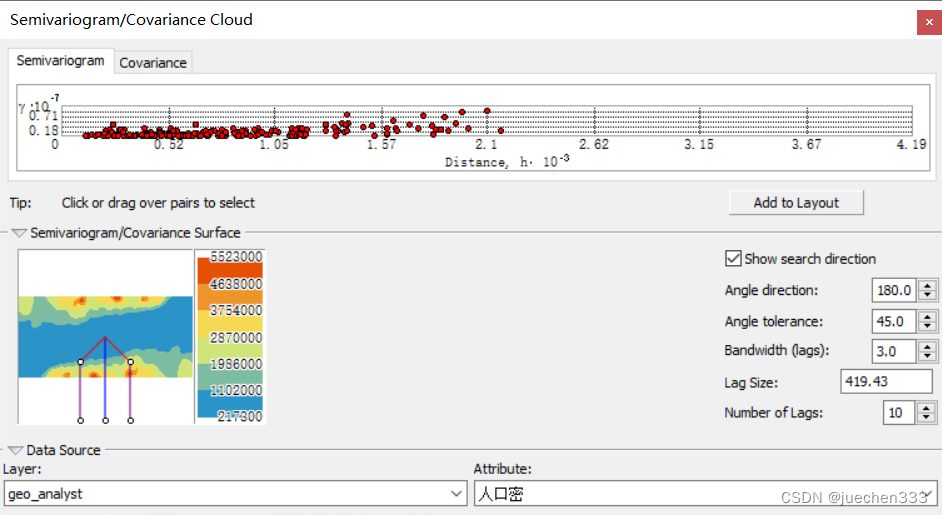
旋转到不同的方向,云图有较为明显的差异,说明数据具有各向异性
(6)点击【ArcToolbox】|【Interpolation】|【Kriging】,Z字段设置为人口密度
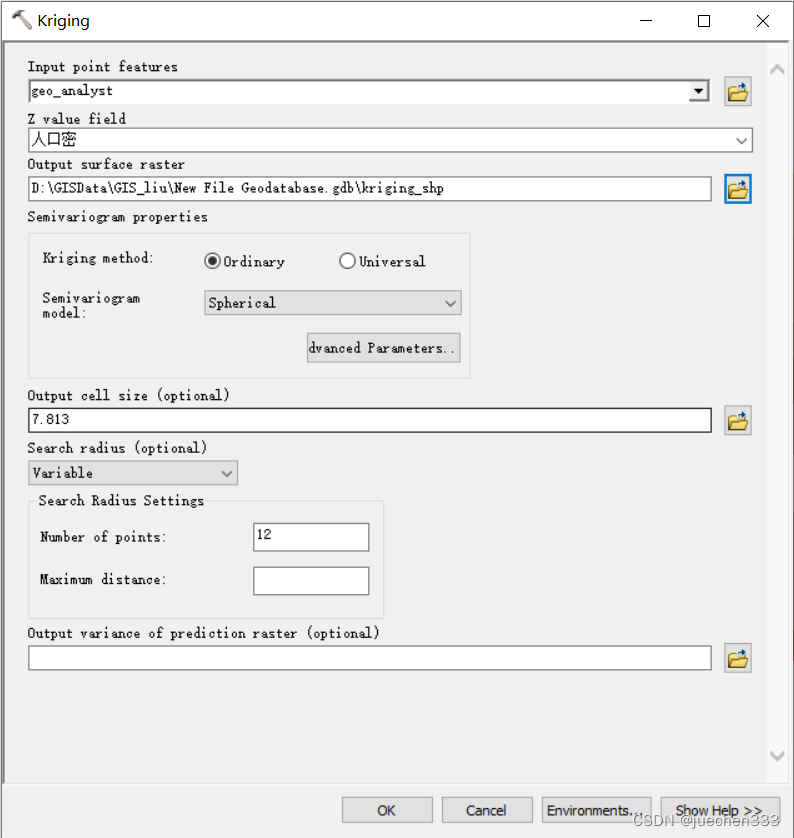
结果为:

实验九 趋势面分析
一、实验目的
了解趋势面分析的基本原理和方法,能够利用工具对数据进行趋势面分析并对结果进行解读。
二、实验数据
同实验八
三、实验内容
利用所给数据进行趋势面分析。
四、实验步骤
(1)加载数据同实验八地统计分析。
(2)打开【Geostatistical Analyst】|【Geostatistical Wizard】,选择【Global Polynomial Interpolation】,【Data】中选择人口密度。
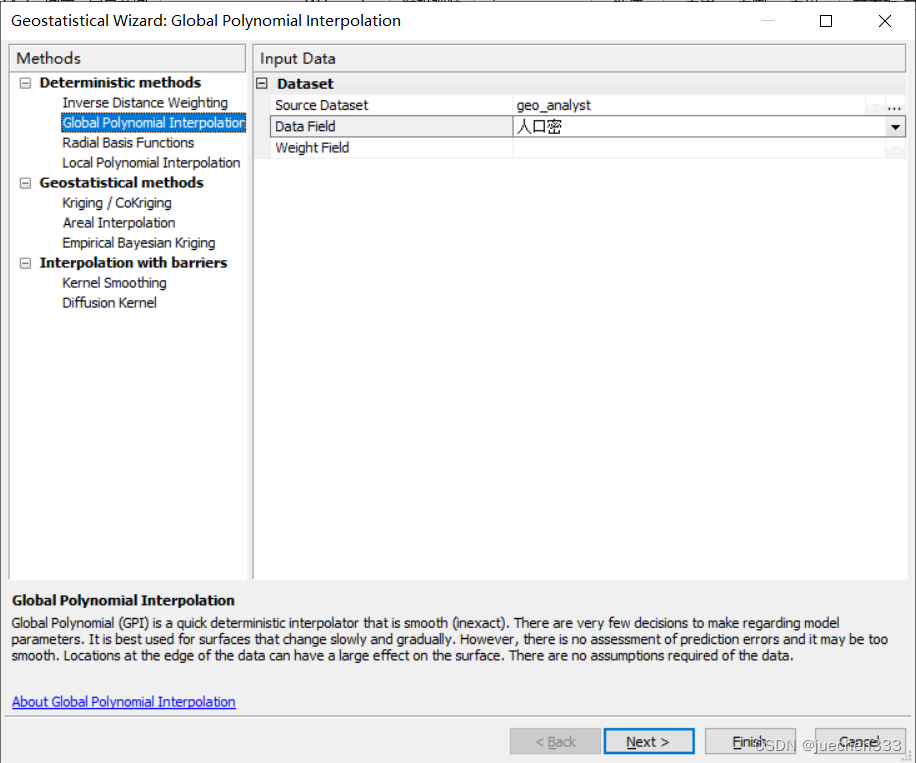
(3)通过调节趋势面模型的幂,找到趋势面均方根的最小值,当幂为3时,效果较好
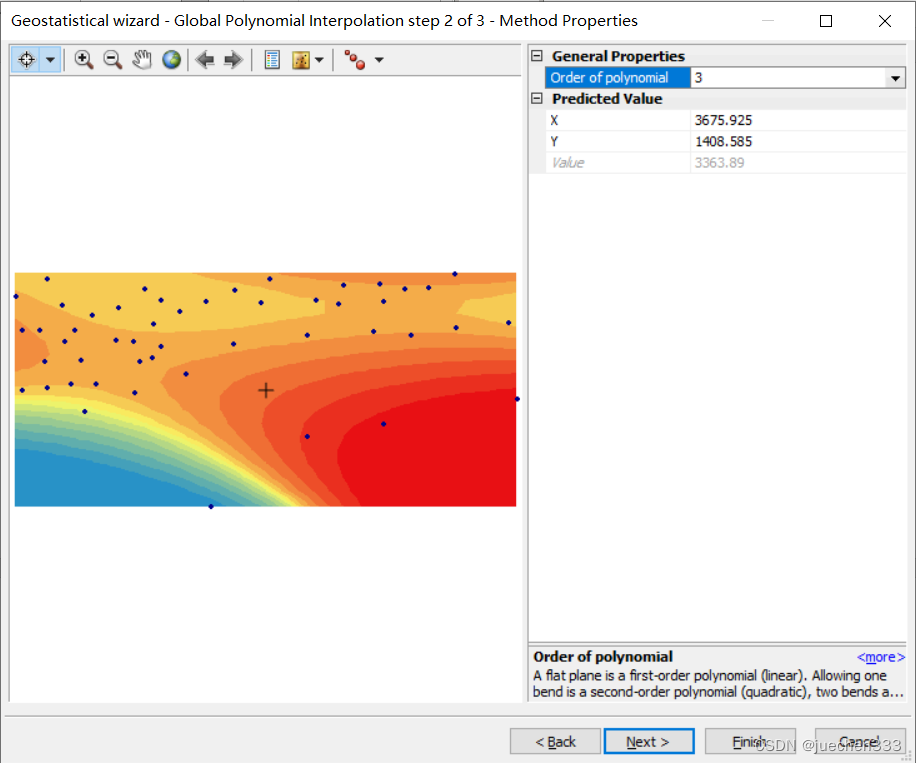
(4)结果

实验十 马尔可夫分析
一、实验目的
了解马尔可夫分析的基本原理和方法,能够利用工具对数据进行马尔科夫分析并对结果进行解读。
二、实验数据
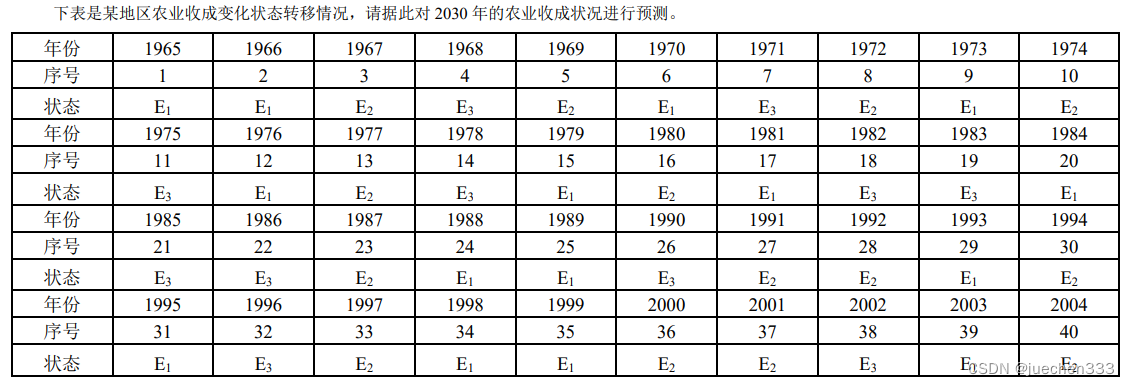
三、实验内容
利用所给数据进行马尔可夫分析。
四、实验步骤
(1)在Excel中将数据进行处理,1代表E1,2代表E2,3代表E3。
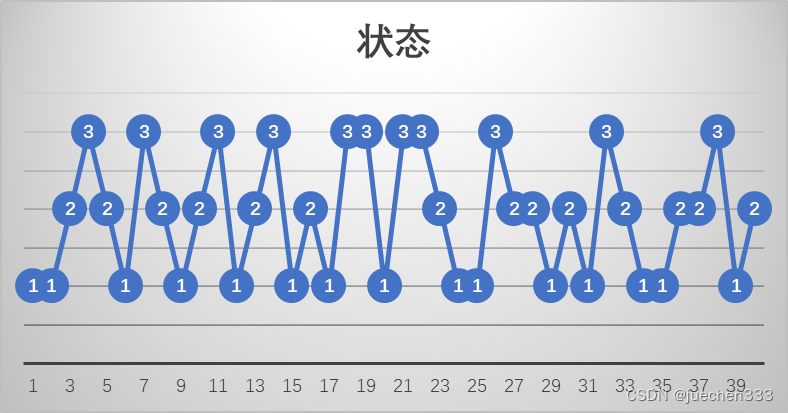
(2)得到转移矩阵
| 当前农业状态 | 下步农业状态 | ||
| E1 | E2 | E3 | |
| E1 | 3 | 7 | 5 |
| E2 | 7 | 2 | 4 |
| E3 | 4 | 5 | 2 |
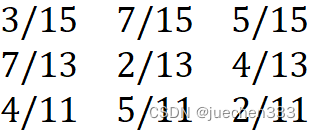
(3)2004年是E2状态,也就是,预测2030年的农业收成,需要求出26步转移矩阵,为此我们需要计算初始转移矩阵的26次方,
借助矩阵在线编辑器矩阵计算器 - Reshish
输入矩阵:

计算结果:
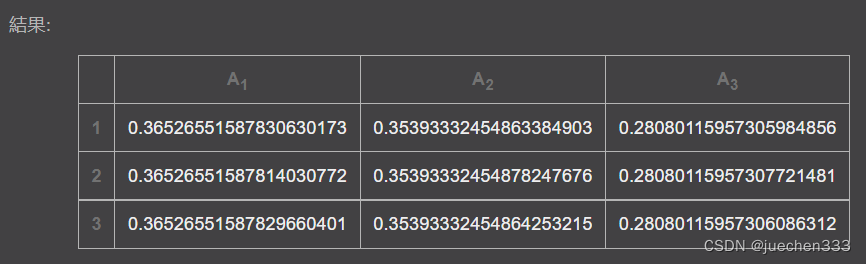
结果矩阵为:

(4)由于2004年的状态向量为(7/13,2/13,4/13),也就是(0.54,0.15,0.31),求出26年后的状态向量
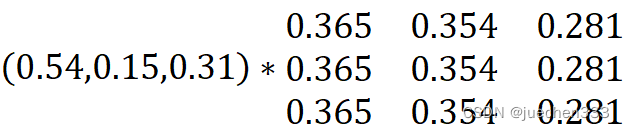
结果为(0.365,0.354,0.281),可知2030年的状态为E1。


