【数据结构与算法】：交换排序之快速排序（手绘图解+LeetCode原题）_快速排序交换法

一、快速排序

1.什么是快速排序？

快速排序是交换排序的一种，本质上快速排序就是采用“分而治之”的策略（分治法），将问题规模减小，再而对问题分别进行处理的排序算法。

2.快速排序的基本原理。

快速排序的原理：在已有元素中，任选一个元素作为“基准”，根据“基准”，将未排序元素划分为两个子序列，一个子序列的元素均小于基准元素，而另一个子序列的元素均大于基准元素，然后递归地对这两个子序列进行排序。

快速排序示意图（44为基准）：

3.实现快速排序的具体过程。

①选取一个元素作为基准，与末尾元素交换位置。
②设置两个指针（Low和High），分别指向首元素与倒数第二个元素。

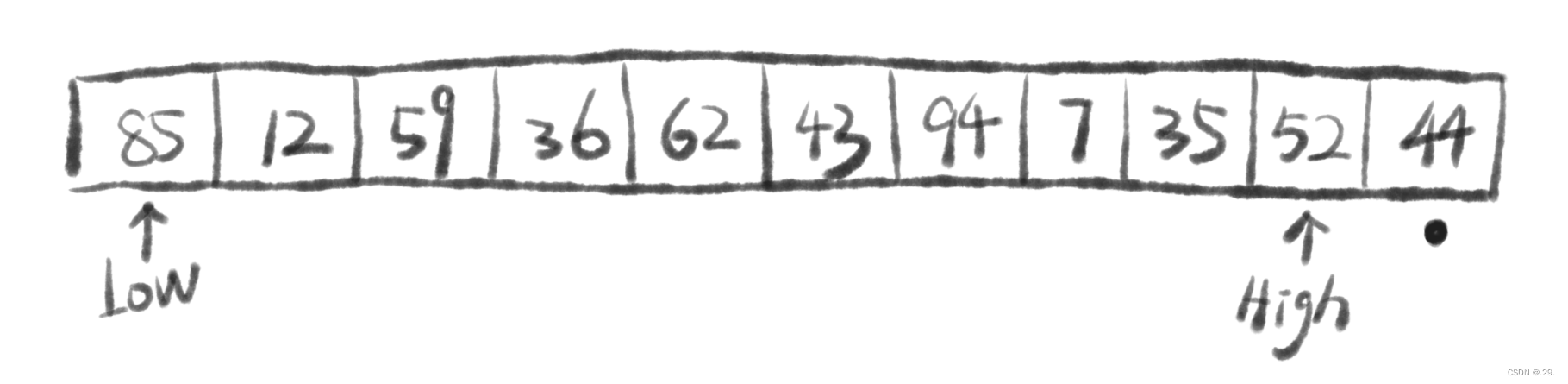
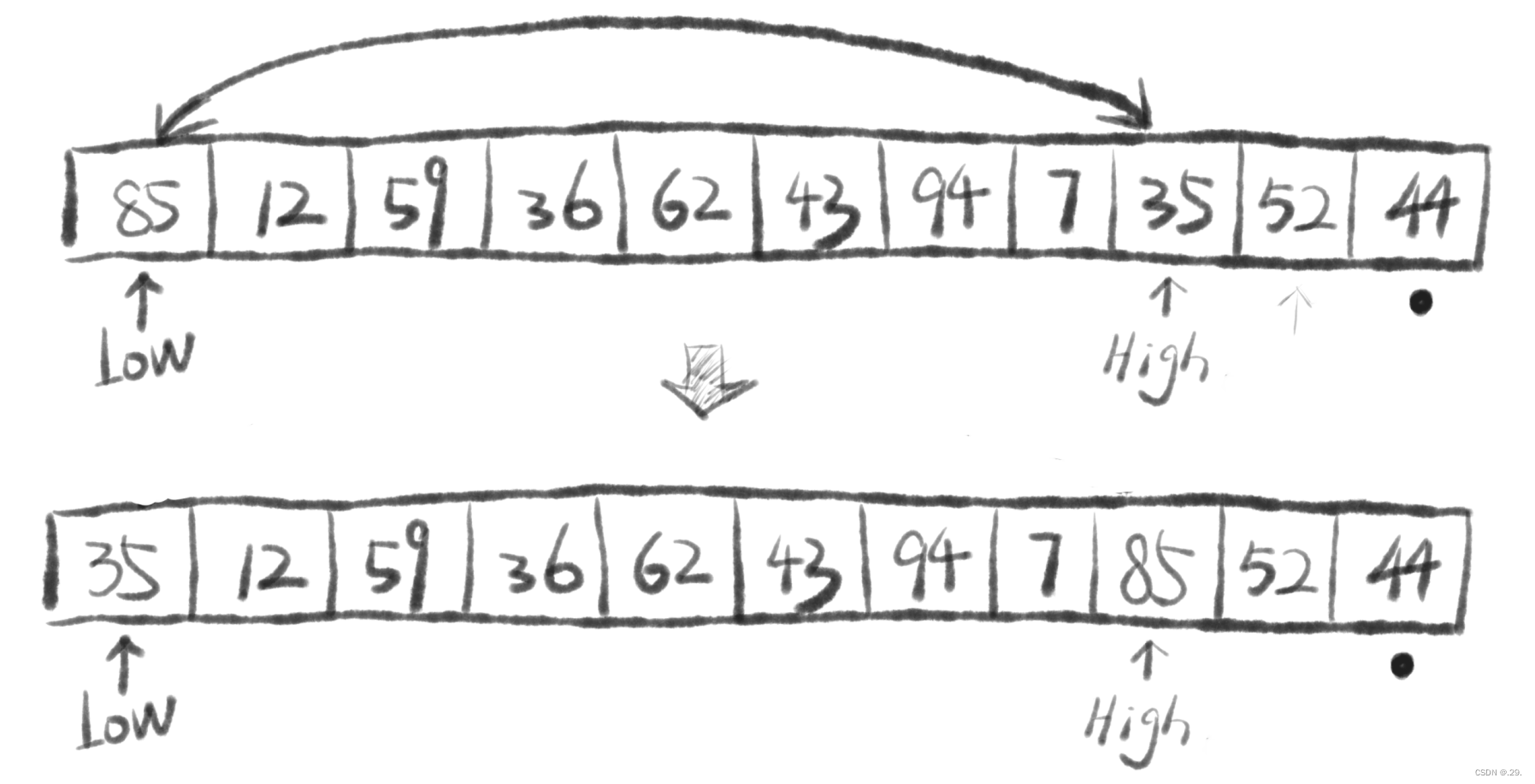
③Low指针由左向右扫描，其位置左侧放置的都是遍历过的或交换过的小于基准的元素；
—High指针从右向左扫描，其位置右侧放置的都是遍历过的或交换过的大于基准的元素。
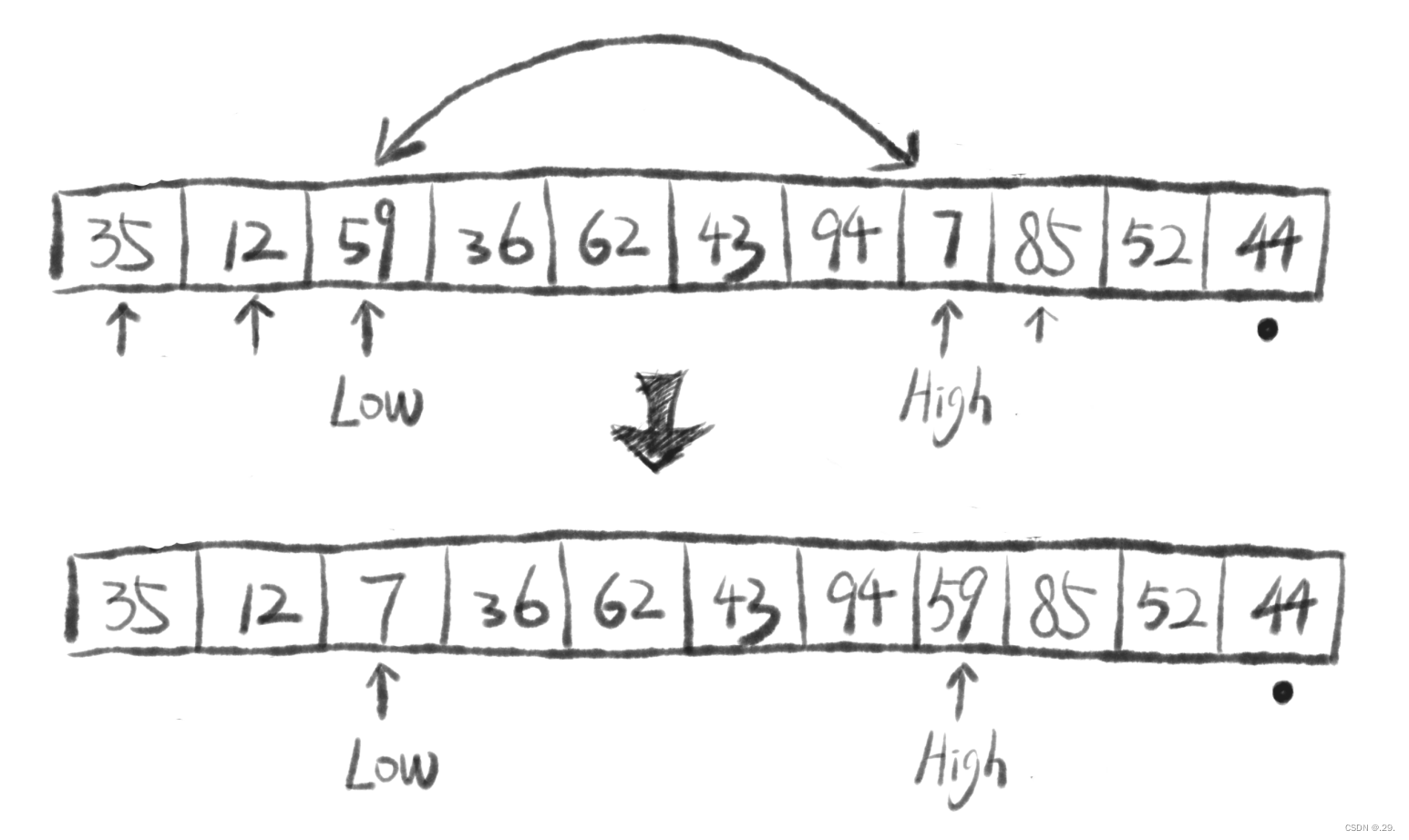
—首先是Low指针向后扫描，遇到大于基准的元素停止；
—然后是High指针向前扫描，遇到小于基准的元素停止。
④在指针还未错位时（在 Low < High 时），将 High 和 Low 指向的元素交换位置。

⑤重复上述操作，直至 High指针 和 Low指针 错位




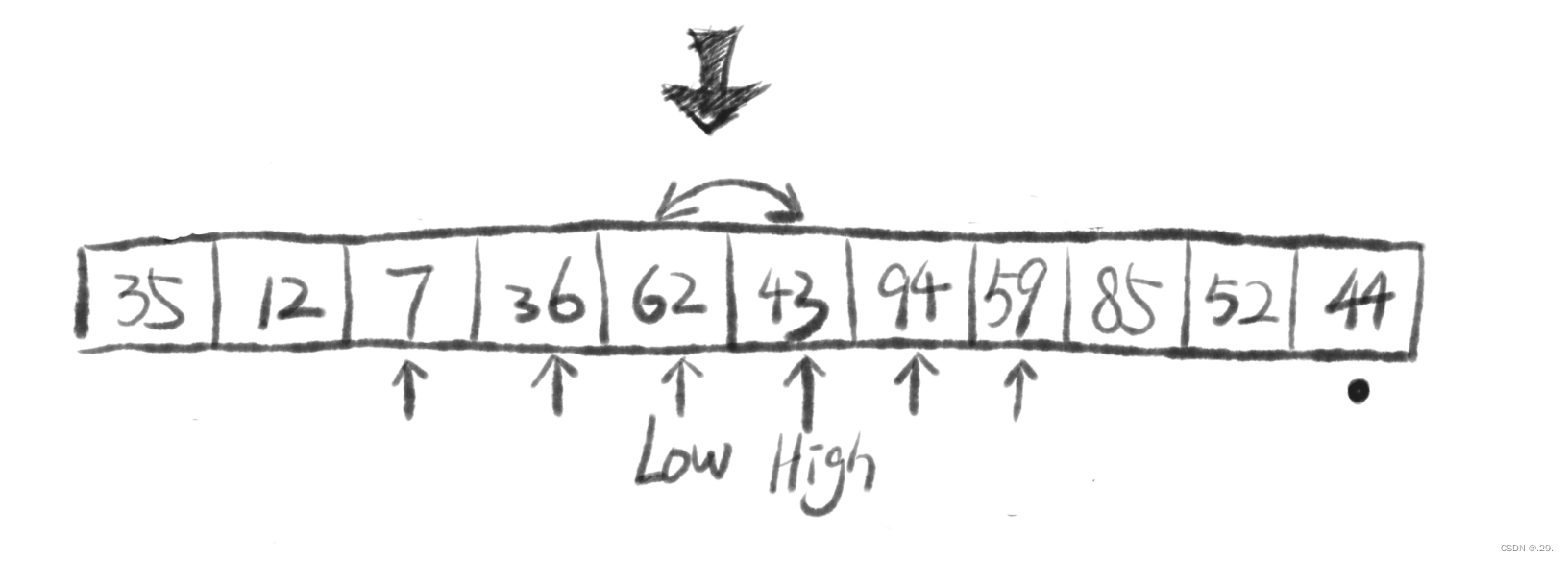
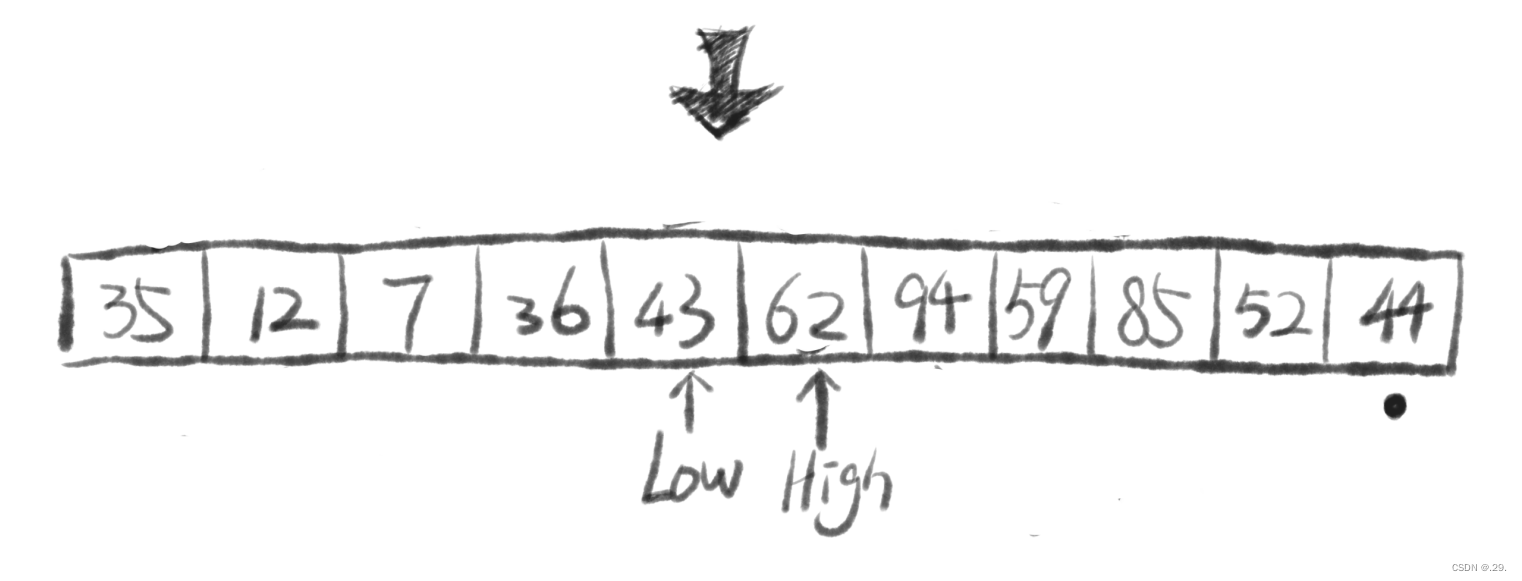
⑥错位后停止，将基准元素与指针Low指向元素交换位置，至此，我们成功将小于基准的元素放在其左，大于基准的元素放于其右！
——这代表我们成功完成了一次划分，以基准为边界分别划分成小于和大于基准的两个子序列。

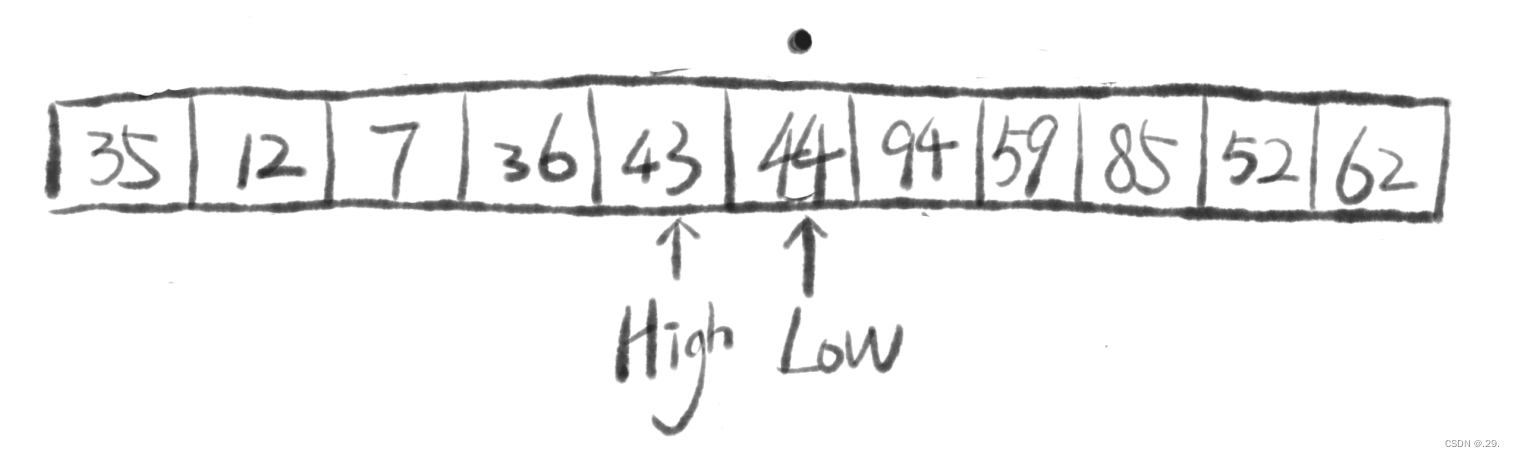
⑦递归地对两个子序列，用同样的方法进行快速排序即可。

二、算法优化

需注意：
—在特殊情况下，比如在序列基本有序的情况下，若每次划分得到的两个子序列都是1比（N-1）的情况时，快速排序执行时间复杂度接近于冒泡排序的O（N²）。
—为了避免最坏结果，我们需要在下标为Low，High，（Low+High）/ 2的三个元素中取得中间值元素作为序列的基准，这样有可能避免最坏情况。

三、快速排序代码实现（优化后）。

import java.util.Arrays;

/**
 * @author .29.
 * @create 2022-09-09 21:37
 */
public class QuickSort {
    public static void main(String[] args) {
        int[] arr = {85,12,59,36,62,44,43,94,7,35,52};//案例
        String str1 = Arrays.toString(arr);
        Qsort(arr,0,arr.length - 1);        //进行快速排序
        String str2 = Arrays.toString(arr);            //转换为字符串方便输出展示

        System.out.println(str1);                      //原序列输出
        System.out.println(str2);                      //快速排序后
    }

    public static void Qsort(int[] arr,int left,int right){
        if(left < right){
            int Low;                             //左边界
            int High;                            //右边界
            int Pivote;                          //基准
            Pivote = Median3(arr,left,right);    //获取基准

            Low = left;                          //需排序首元素的前一位（后续指针会优先向后移动）
            High = right - 1;                    //需排序尾元素的后一位（后续指针会优先向前移动）
            while(true){
                //指针优先向后移动，指向需排序首元素，若元素小于基准，继续后移
                while(arr[++Low] < Pivote);       
                //指针优先向前移动，指向需排序尾元素，若元素大于基准，继续前移
                while((Low<High) && arr[--High] > Pivote);
                
                if(Low < High) swap(arr,Low,High);//指针未错位，停止扫描后，元素交换位置
                else break;                       //指针错位，结束循环
            }

            if(Low < right)
            swap(arr,right-1,Low);              //将基准与错位后的Low指向元素交换位置

            Qsort(arr,left,Low-1);          //递归地对划分好的左序列用同样方法快速排序
            Qsort(arr,Low+1,right);          //递归地对划分好的右序列用同样方法快速排序
        }
        }

    //用来交换元素的方法（函数）
    public static void swap(int[] arr,int i,int j){
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
    
    public static int Median3(int[] arr,int left,int right){
        int center = left + ((right-left) >> 1);      //相当于（left+right）/2
        if(arr[left] > arr[center])         //如果首元素小于中间元素
            swap(arr,left,center);           //交换位置

        if(arr[left] > arr[right])          //如果首元素小于尾元素
            swap(arr,left,right);            //交换位置

        if(arr[center] > arr[right])        //如果中间元素小于尾元素
            swap(arr,center,right);          //交换位置
        
        //经过上述操作，此时arr[left] <= arr[center] <= arr[right]
        //将基准放置在倒数倒数第一个元素（不放在最后是因为末尾的arr[right]大于基准
        swap(arr,center,right - 1);
        //现在首元素小于基准，尾元素大于基准，只需要考虑left+1到right-2的情况（right-1是基准）
        return arr[right-1];//返回被选为基准的元素
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

控制台输出：

四、算法分析

时间复杂度

快速排序时间复杂度分析较为复杂。
最好情况下，每次划分都得到等长的子序列，每一层递归比较的时间复杂度为O（N），而递归层次深度为O（log₂N），即最好情况是O（Nlog₂N）。
最差时间复杂度上文有解释过，为O（N²）。

五、快排思想在实际题目中的运用

（更新于：2022.9.10）

题目一、剑指Offer 40.最小的k个数

LeetCode原题链接：剑指Offer 40.最小的k个数
题目描述：

输入整数数组 arr ，找出其中最小的 k 个数。
例如，输入4、5、1、6、2、7、3、8这8个数字，则最小的4个数字是1、2、3、4。

示例 1：
输入：arr = [3,2,1], k = 2
输出：[1,2] 或者 [2,1]

示例 2：
输入：arr = [0,1,2,1], k = 1
输出：[0]
1
2
3
4
5
6
7
8
9
10

解题思路：
经过上文的讲解，我们知道了，快速排序就是选定一个基准，通过一定操作让小于基准的元素放在基准左侧子序列，将大于基准的元素放在基准右侧子序列的排序算法。

题目的要求是：找出数组中最小的k个数，是不是觉得有什么地方十分相似？当我们的第k个数是快速排序的基准时，加上基准左侧的子序列，正是要求的最小的k个数…

所以解决问题的关键点就在于：
我们把基准及其左侧子序列的元素个数记作num
当num等于预期需要的数量k，输出划分好的序列即可。
当num大于预期需要的数量k，我们递归地对左序列进行同样的快排操作。
当num小于预期需要的数量k，我们递归地对基准之后与第k个元素之前的序列进行操作。（此时预期的数量就变为k-num了，因为num个数已经划分好，只需要划分剩下的元素，直至达到预期）

建议在理解代码时，画图辅助理解，特别是快排划分的那部分，有助于清晰地理解快排划分左子序列的具体过程。

实现代码：

class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        Qselect(arr,0,arr.length-1,k);//利用快排思想，将最小的k个数放在序列前列
        int[] Oput = new int[k];      //开辟一个大小为K的空间
        for(int i = 0;i < k; ++i){    //循环地将最小的k个数放入空间
            Oput[i] = arr[i];
        }
        return Oput;                 
    }

    //快速选择的递归函数（方法）
    public void Qselect(int[] arr,int L,int R,int k){
        if(L >= R)                           
        return;

        int p = getPivote(arr,L,R);      //获取基准元素下标
        int num = p-L+1;                 //左侧小于基准的子序列的元素个数
        //（基准划分的 左子序列元素 <= 基准 < 右子序列元素）
            if(num == k ){               //若左子序列元素个数等于预期的数量k
                return;                  //直接返回的就是最小的k个数
            }else if(num > k){           //若左子序列元素个数超过预期的数量k
                Qselect(arr,L,p-1,k);    //递归地用快速排序继续划分序列
            }else{                       //若左子序列元素个数低于预期的数量k
            //递归地用快速排序划分基准右侧的序列，除去已划分好的个数num，预期数量改为k-num
                Qselect(arr,p+1,R,k-num);
            }
    }

    //随机选取基准，并用于快排的函数（方法）
    public int getPivote(int[] arr,int L,int R){
        int pivote = (int)(Math.random()*(R-L+1)+L);//序列中任取元素为基准
        swap(arr,pivote,R);                         //基准与尾元素交换
        return Qsort(arr,L,R);                      //完成一次快排划分，返回基准
    }

    //快速排序的函数（只考虑左子序列的情况）
    //此方法建议画图辅佐理解
    public int Qsort(int[] arr,int L,int R){
        int Low = L-1;                      //小于区域的边界
        int High = R;                       //尾元素，即基准元素下标
        for(int l = L;l < High; l++){       //从左向右扫描
            if(arr[l] <= arr[High]){        //如果扫过元素小于基准元素，即符合要求
                Low++;                      //小于区域边界向右移动
                swap(arr,Low,l);            //交换区域边界元素与扫过的元素
 //说明：当边界内元素小于基准，相当于与自身交换，当边界内元素大于基准，相当于将小于基准的元素换进来
            }
        }
        swap(arr,R,Low+1);                 //将基准与小于区域的下一位交换位置，表示完成一次划分
            return Low+1;                  //返回记住下标。
    }

    //用于交换元素位置的函数（方法）
    public void swap(int[] arr,int i,int j){
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

提交结果：

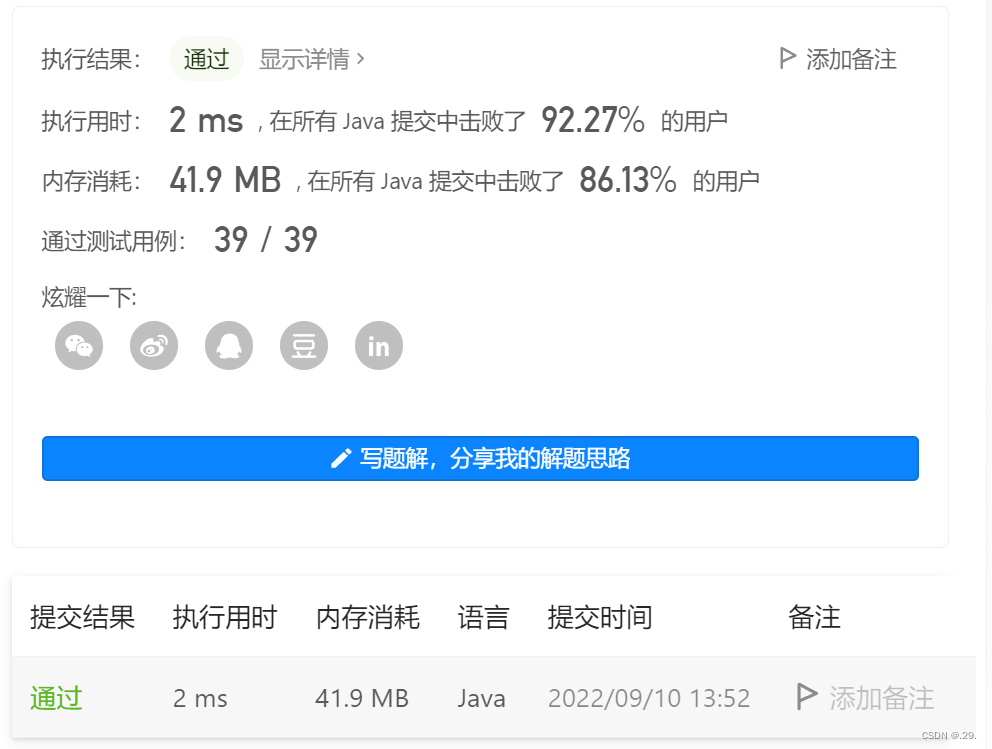
总结，只要理解了基本的解题思路，问题就不算难，重要的还是要记住快速排序的基本模式是如何的。