stable diffusion代码学习笔记

前言：本文没有太多公式推理，只有一些简单的公式，以及公式和代码的对应关系。本文仅做个人学习笔记，如有理解错误的地方，请指出。

本文包含stable diffusion入门文献和不同版本的代码。

文献资源

1. 本文学习的代码；
2. 相关文献：

• Denoising Diffusion Probabilistic Models : DDPM，这个是必看的，推推公式
• Denoising Diffusion Implicit Models ：DDIM，对 DDPM 的改进
• Pseudo Numerical Methods for Diffusion Models on Manifolds ：PNMD/PLMS，对 DDPM 的改进
• High-Resolution Image Synthesis with Latent Diffusion Models ：Latent-Diffusion，必看
• Neural Discrete Representation Learning ： VQVAE，简单翻了翻，示意图非常形象，很容易了解其做法

代码资源

1. stable diffusion v1.1-v1.4， https://github.com/CompVis/stable-diffusion
2. stable diffusion v1.5，https://github.com/runwayml/stable-diffusion
3. stable diffusion v2，https://github.com/Stability-AI/stablediffusion
4. stable diffusion XL，https://github.com/Stability-AI/generative-models

前向过程（训练）

• 输入一张图片+随机噪声，训练unet，网络预测图片加上的噪声

反向过程（推理）

• 给个随机噪声，不断迭代去噪，输出一张图片

总体流程

• 输入的prompt经过clip encoder编码成(3+3,77,768)特征，正负prompt各3个，默认negative prompt为空‘’，解码时正的和负的latent图片用公式计算一下才是最终结果；time step通过linear层得到(3+3,1280)特征；把prompt和time ebedding和随机生成的图片放入unet，得到的就是我们要的图片。

采样流程 text2img

• 该函数在PLMSSampler中，输入x(噪声，(3,4,64,64))-----c（输入的prompt，(3,77,768)----t （输入的time step，第几次去噪(3,)。把这三个东西输入unet，得到预测的噪声e_t。

 def p_sample_plms(self, x, c, t, index, repeat_noise=False, use_original_steps=False, quantize_denoised=False,
                      temperature=1., noise_dropout=0., score_corrector=None, corrector_kwargs=None,
                      unconditional_guidance_scale=1., unconditional_conditioning=None, old_eps=None, t_next=None):
        b, *_, device = *x.shape, x.device

        def get_model_output(x, t):
            if unconditional_conditioning is None or unconditional_guidance_scale == 1.:
                e_t = self.model.apply_model(x, t, c)
            else:
                x_in = torch.cat([x] * 2)
                t_in = torch.cat([t] * 2)
                c_in = torch.cat([unconditional_conditioning, c]) # 积极消极的prompt，解码时按照公式减去消极prompt的图像
                e_t_uncond, e_t = self.model.apply_model(x_in, t_in, c_in).chunk(2)
                e_t = e_t_uncond + unconditional_guidance_scale * (e_t - e_t_uncond)

            if score_corrector is not None:
                assert self.model.parameterization == "eps"
                e_t = score_corrector.modify_score(self.model, e_t, x, t, c, **corrector_kwargs)

            return e_t

        alphas = self.model.alphas_cumprod if use_original_steps else self.ddim_alphas
        alphas_prev = self.model.alphas_cumprod_prev if use_original_steps else self.ddim_alphas_prev
        sqrt_one_minus_alphas = self.model.sqrt_one_minus_alphas_cumprod if use_original_steps else self.ddim_sqrt_one_minus_alphas
        sigmas = self.model.ddim_sigmas_for_original_num_steps if use_original_steps else self.ddim_sigmas

        def get_x_prev_and_pred_x0(e_t, index):
            # select parameters corresponding to the currently considered timestep
            a_t = torch.full((b, 1, 1, 1), alphas[index], device=device)
            a_prev = torch.full((b, 1, 1, 1), alphas_prev[index], device=device)
            sigma_t = torch.full((b, 1, 1, 1), sigmas[index], device=device)
            sqrt_one_minus_at = torch.full((b, 1, 1, 1), sqrt_one_minus_alphas[index],device=device)

            # current prediction for x_0
            pred_x0 = (x - sqrt_one_minus_at * e_t) / a_t.sqrt()
            if quantize_denoised:
                pred_x0, _, *_ = self.model.first_stage_model.quantize(pred_x0)
            # direction pointing to x_t
            dir_xt = (1. - a_prev - sigma_t**2).sqrt() * e_t
            noise = sigma_t * noise_like(x.shape, device, repeat_noise) * temperature
            if noise_dropout > 0.:
                noise = torch.nn.functional.dropout(noise, p=noise_dropout)
            x_prev = a_prev.sqrt() * pred_x0 + dir_xt + noise
            return x_prev, pred_x0

        e_t = get_model_output(x, t) # 模型预测的噪声
        if len(old_eps) == 0:
            # Pseudo Improved Euler (2nd order)
            x_prev, pred_x0 = get_x_prev_and_pred_x0(e_t, index) # 输入噪声减去预测噪声得到新的噪声，当前预测的latent图片
            e_t_next = get_model_output(x_prev, t_next)
            e_t_prime = (e_t + e_t_next) / 2 # 两次噪声的均值？
        elif len(old_eps) == 1:
            # 2nd order Pseudo Linear Multistep (Adams-Bashforth)
            e_t_prime = (3 * e_t - old_eps[-1]) / 2
        elif len(old_eps) == 2:
            # 3nd order Pseudo Linear Multistep (Adams-Bashforth)
            e_t_prime = (23 * e_t - 16 * old_eps[-1] + 5 * old_eps[-2]) / 12
        elif len(old_eps) >= 3:
            # 4nd order Pseudo Linear Multistep (Adams-Bashforth)
            e_t_prime = (55 * e_t - 59 * old_eps[-1] + 37 * old_eps[-2] - 9 * old_eps[-3]) / 24

        x_prev, pred_x0 = get_x_prev_and_pred_x0(e_t_prime, index)

        return x_prev, pred_x0, e_t
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

• 接下来看公式：
  
• 网络得到e_t后，进入到get_x_prev_and_pred_x0函数，可以看到pred_x0 = (x - sqrt_one_minus_at * e_t) / a_t.sqrt()就是上述公式，也就是说网络的预测结果通过公式计算，我们可以得到预测的pred_x0原始图片和前一刻的噪声图像x_prev。

        def get_x_prev_and_pred_x0(e_t, index):
            # select parameters corresponding to the currently considered timestep
            a_t = torch.full((b, 1, 1, 1), alphas[index], device=device)
            a_prev = torch.full((b, 1, 1, 1), alphas_prev[index], device=device)
            sigma_t = torch.full((b, 1, 1, 1), sigmas[index], device=device)
            sqrt_one_minus_at = torch.full((b, 1, 1, 1), sqrt_one_minus_alphas[index],device=device)

            # current prediction for x_0
            pred_x0 = (x - sqrt_one_minus_at * e_t) / a_t.sqrt()
            if quantize_denoised:
                pred_x0, _, *_ = self.model.first_stage_model.quantize(pred_x0)
            # direction pointing to x_t
            dir_xt = (1. - a_prev - sigma_t**2).sqrt() * e_t
            noise = sigma_t * noise_like(x.shape, device, repeat_noise) * temperature
            if noise_dropout > 0.:
                noise = torch.nn.functional.dropout(noise, p=noise_dropout)
            x_prev = a_prev.sqrt() * pred_x0 + dir_xt + noise
            return x_prev, pred_x0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

• 前一刻的噪声图像的推理公式如图：
  
  

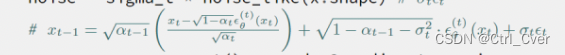
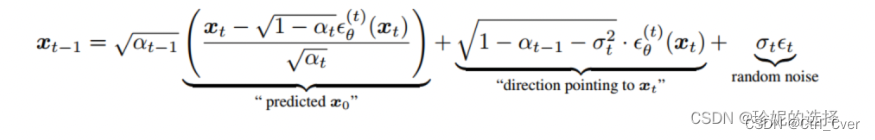
• 得到了上一刻的噪声图片x_prev后(也就是函数返回的img)，继续迭代，最终生成需要的图片。
  

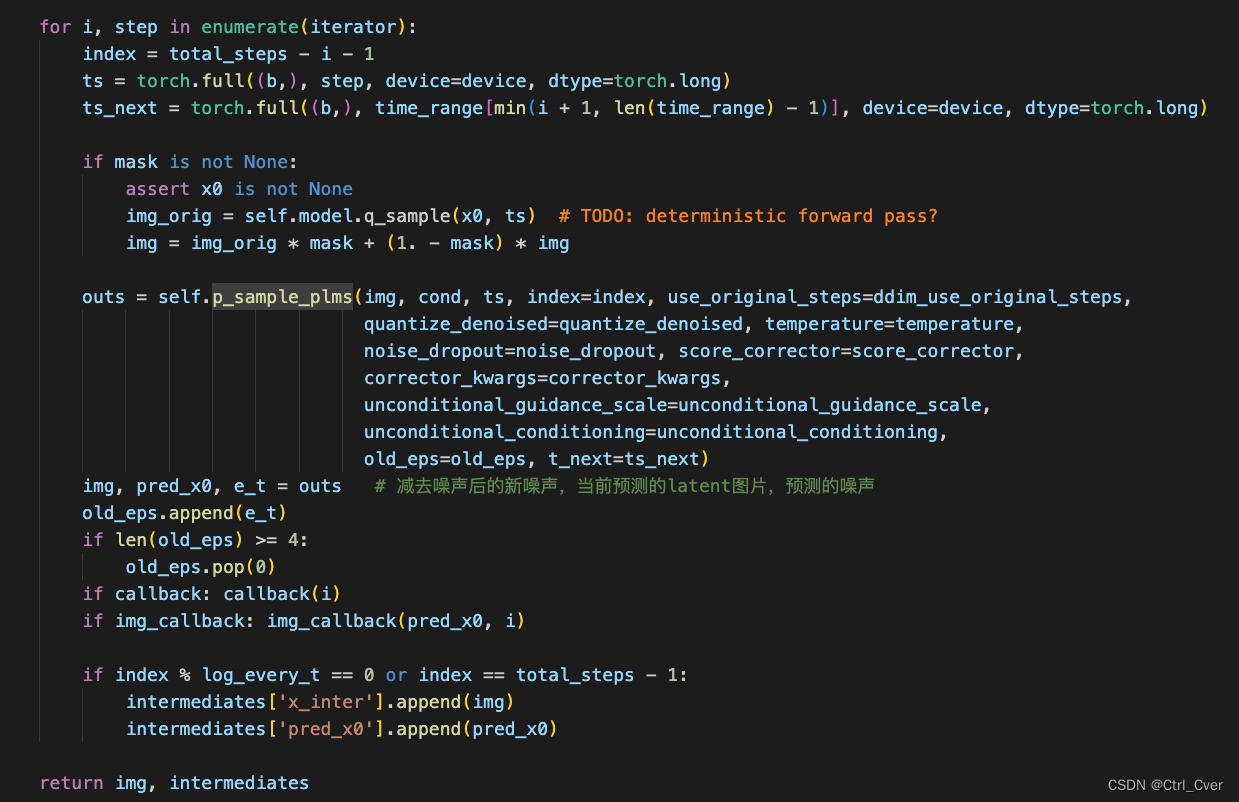
额外说明

这部分代码应该就是PLMS加速采样用的，论文中有公式推理

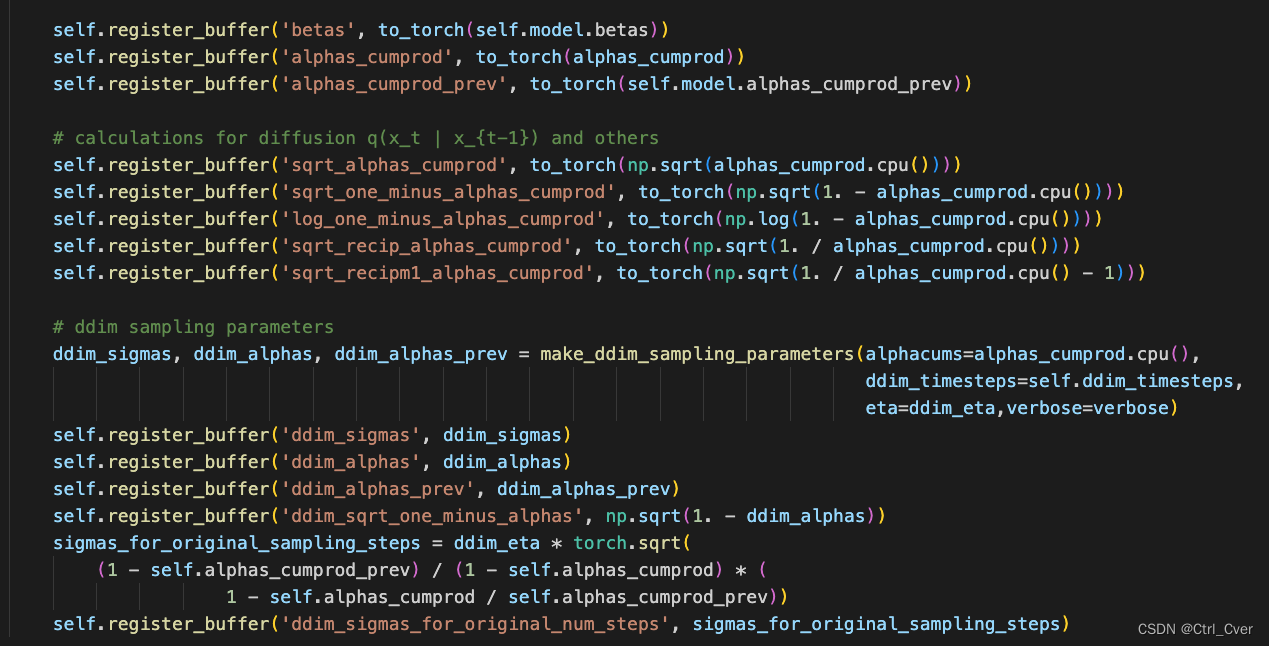
另外，还有一些参数是训练时候保存的，betas逐渐增大，用来控制噪声的强度。变量名解析 log_one_minus_alphas_cumprod其实就是log(1-alpha(右下角t)(头上直线))，没有带prev的都是当前时刻t，带prev的是前一时刻t-1。

参考文献：

https://blog.csdn.net/Eric_1993/article/details/129600524?spm=1001.2014.3001.5502
https://zhuanlan.zhihu.com/p/630354327