布隆过滤器Bloom Filter简介_布隆过滤器假阳性了怎么办

背景：

如果在平时我们要判断一个元素是否在一个集合中，通常会采用查找比较的方法，下面分析不同的数据结构查找效率：

• 采用线性表存储，查找时间复杂度为O(N)
• 采用平衡二叉排序树（AVL、红黑树）存储，查找时间复杂度为O(logN)
• 采用哈希表存储，考虑到哈希碰撞，整体时间复杂度也要O[log(n/m)]

当需要判断一个元素是否存在于海量数据集合中，不仅查找时间慢，还会占用大量存储空间，接下来看一下布隆过滤器如何解决这个问题

 

1、什么是布隆过滤器：

布隆过滤器是一种空间效率很高的随机数据结构，专门用来检测集合中是否存在特定的元素。布隆过滤器由一个长度为m比特的位数组与k个独立的哈希函数组成的数据结构。位数组初始化均为0，所有的哈希函数都可以分别把输入数据尽量均匀地散列。当要向布隆过滤器中插入一个元素时，该元素经过k个哈希函数计算产生k个哈希值，以哈希值作为位数组中的下标，将所有k个对应的比特值由0置为1。当要查询一个元素时，同样将其经过哈希函数计算产生哈希值，然后检查对应的k个比特值：如果有任意一个比特为0，表明该元素一定不在集合中；如果所有比特均为1，表明该元素有可能性在集合中。

由于可能出现哈希碰撞，不同元素计算的哈希值有可能一样，导致一个不存在的元素有可能对应的比特位为1，这就是所谓“假阳性”（false positive）。相对地，“假阴性”（false negative）在BF中是绝不会出现的。因此，Bloom Filter不适合那些“零错误”的应用场合。而在能容忍低错误率的应用场合下，Bloom Filter通过极少的错误换取了存储空间的极大节省。

所以，布隆过滤器认为不在的，一定不会在集合中；布隆过滤器认为在的，不一定存在集合中。

2、算法实现步骤：

• （1）选取k个哈希函数，记为 {h1,h2,…,hk}，至于参数k的选择问题，我后面再说。
• （2）假设现在有n个元素需要被映射到bit数组中，bit数组的长度是m。初始时，将m位的bit数组的每个位置的元素都置为0。一样地，关于参数m的选择我之后说。
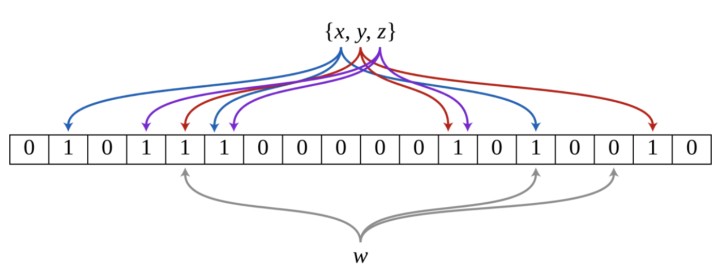
• （3）现在，把这个n个元素依次用第1步选取的k个哈希函数映射到bit数组的位置上，bit数组被映射到的位置的元素变为1。显然，一个元素能被映射到k个位置上。过程如图所示，现在把元素集合{x,y,z}通过3个哈希函数映射到一个二进制数组中。
• （4）最后，需要检查一个元素是否在已有的集合中时，同样用这k个哈希函数把要判断的元素映射到bit数组的位置上，只要bit数组被映射到的位中有一个位不是1，那一定说明了这个元素不在已有的集合内。如图所示，检查w是否在集合中时，有一个哈希函数将ww映射到了bit数组的元素为0的位置。

3、布隆过滤器优缺点

（1）优点：

• 节省空间：不需要存储数据本身，只需要存储数据对应hash比特位
• 时间复杂度低：插入和查找的时间复杂度都为O(k)，k为哈希函数的个数

（2）缺点：

• 存在假阳性：布隆过滤器判断存在，但可能出现元素实际上不在集合中的情况；误判率取决于哈希函数的个数，对于哈希函数的个数选择，我们第4部分会讲
• 不支持删除元素：如果一个元素被删除，但是却不能从布隆过滤器中删除，这也是存在假阳性的原因之一

4、参数的选择：

假设E表示错误率，n表示要插入的元素个数，m表示bit数组的长度，k表示hash函数的个数。

（1）当hash函数个数 k = (ln2) * (m/n)时，错误率E最小（此时bit数组中有一半的值为0）

（2）在错误率不大于E的情况下，bit数组的长度m需要满足的条件为：m ≥ n * lg(1/E)。

（3）结合上面两个公式，在hash函数个数k取到最优时，要求错误率不大于E，这时我们对bit数组长度m的要求是：m>=nlg(1/E) * lg(e) ，也就是 m ≥ 1.44n*lg(1/E)（lg表示以2为底的对数）

这里我给这几个参数最终的结论，对这几个参数的推导过程有兴趣的读者，可以阅读这篇文章：https://blog.csdn.net/guoziqing506/article/details/52852515

5、布隆过滤器的应用场景：

• 爬虫系统url去重
• 垃圾邮件过滤
• 黑名单

问题实例：

给你A，B两个文件，各存放50亿条URL，每条URL占用64字节，内存限制是4G，让你找出A,B文件共同的URL。如果是三个乃至n个文件呢？ 

如果允许找过的URL有一定的错误率，那么我们可以使用布隆过滤器来实现。根据这个问题我们来计算下内存占用，4G = 2^32大概是40亿*8大概是340亿的bit数组，n=50亿，如果按出错率0.01算需要的大概是650亿个bit。 现在可用的是340亿，相差并不多，这样可能会使出错率上升些。另外如果这些urlip是一一对应的，就可以转换成ip，则大大简单了。 

具体做法就是：将其中一个文件中的url使用Bloom filter映射为这340亿bit，然后挨个读取另外一个文件的url，检查是否与Bloom filter，如果是，那么该url应该是共同的url

5、如何解决布隆过滤器不支持删除的问题：

（1）counting bloom filter：

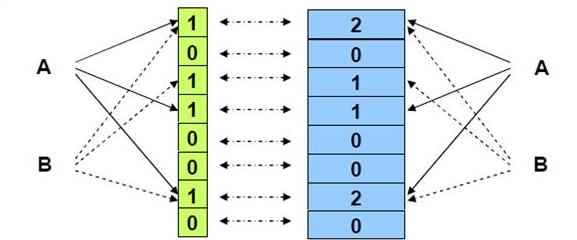
Counting Bloom Filter将标准 Bloom Filter位数组的每一位扩展为一个小的计数器（counter），在插入元素时给对应的k（k为哈希函数个数）个Counter的值分别加1，删除元素时给对应的k个Counter的值分别减1。Counting Bloom Filter通过多占用几倍的存储空间的代价，给Bloom Filter增加了删除操作。

（2）布谷鸟过滤器:

对于这种方式有兴趣的读者可以阅读这篇文章：https://juejin.cn/post/6924636027948630029#heading-1