- 1OceanBase 分布式数据库【信创/国产化】- OceanBase 平台产品 - 迁移评估工具 OMA
- 2c语言怎么超过java了_C语言与java 20155317 王新玮第二次
- 3Python机器学习之k-means聚类算法_python kmeans聚类算法
- 4java 字符串输出字符_输出java字符串
- 513、微信小程序:上传图片到服务器_微信小程序上传图片到服务器
- 6Mysql查看表的元数据信息
- 7sqlite3数据库最大可以是多大?可以存放多少数据?读写性能怎么样?详述
- 8web3系列———4.编写第一个智能合约并发布到链上_remixweb3
- 9Android 蓝牙 HFP通话、三方通话、Sco、rfcomm连接、SLC服务水平连接介绍 - 史上最全分析_蓝牙slc连接
- 10常见数据库分类介绍及其适用场景_数据库常用的类
【海量数据挖掘/数据分析】 之 关联规则挖掘 Apriori 算法 (数据集、事务、频繁项集、关联规则、支持度、置信度)_apriori算法
赞
踩
【海量数据挖掘/数据分析】 之 关联规则挖掘 Apriori 算法 (数据集、事务、频繁项集、关联规则、支持度、置信度)
目录
【海量数据挖掘/数据分析】 之 关联规则挖掘 Apriori 算法 (数据集、事务、频繁项集、关联规则、支持度、置信度)
二、 数据集 与 事务 ( Transaction ) 概念
二十一、使用 Apriori 算法,求 频繁项集 和 关联规则
一、 关联规则挖掘简介
Apriori 算法 是 关联规则 挖掘算法 ,
关联规则 反映了 对象之间 相互依赖关系 ,
可以通过 一个对象 的行为或属性 预测 其它对象的行为或属性 ;
关联规则 不是 因果关系 , 有可能有因果关系 , 有可能没有 ;
如 : 购买商品时 , 啤酒 与 尿布 就有关联关系 , 这两个之间肯定没有因果关系 , 有一种未知的关联关系 ;
关联规则挖掘步骤 :
① 步骤一 : 找出 支持度 ≥ 最小支持度阈值 的 频繁项集 ;
② 步骤二 : 根据 频繁模式 生成 满足 可信度阈值 的 关联规则 ;
二、 数据集 与 事务 ( Transaction ) 概念
数据挖掘 数据集 由 事务 构成 ;
数据集 记做 D ;
使用事务表示 数据集 , 表示为 D = { t 1 , t 2 , ⋯ , t n } D = \{ t_1 , t_2 , \cdots , t_n \} D={t1,t2,⋯,tn} ,
其中 tk , ( k = 1 , 2 , ⋯ , n ) 称为事务 ;
每个事物可以使用 唯一的标识符 表示 事务编号 ( TID ) ;
三、项 ( Item ) 概念
每个 事务 ( Transaction ) 由多个 项 ( Item ) 组成 ;
项 记做 i ;
表示为 t k = { i 1 , i 2 , ⋯ , i n } ;
数据集 D 是所有 项 i 的集合 是 I 集合 ;
四、项集 ( Item Set ) 概念
I 中的 任意子集 X , 称为 数据集 D 的 项集 ( Item Set ) ;
如果 项集 ( Item Set ) 中 项 ( Item ) 个数为 k ,
则称该 项集 ( Item Set ) 为 k 项集 ( k-itemset ) ;
五、频繁项集
频繁项集 : 频繁项集指的是出现次数较多的项集 ;
六、数据集、事物、项、项集合、项集 示例

整个 数据集 D , 由 5 个 事务 构成 ;
数据集 : D = { t 1 , t 2 , t 3 , t 4 , t 5 }
事物 1 : t 1 = { 奶 粉 , 莴 苣 }
事物 2: t 2 = { 莴 苣 , 尿 布 , 啤 酒 , 甜 菜 }
事物 3 : t 3 = { 奶 粉 , 尿 布 , 啤 酒 , 橙 汁 }
事物 4 : t 4 = { 奶 粉 , 莴 苣 , 尿 布 , 啤 酒 }
事物 5 : t 5 = { 奶 粉 , 莴 苣 , 尿 布 , 橙 汁 }
上述 事物 集合中的元素 i 都称为项 , 奶粉,莴苣,尿布,啤酒,甜菜,橙汁 都是 项 ;
I = { 奶 粉 , 莴 苣 , 尿 布 , 啤 酒 , 甜 菜 , 橙 汁 }
项集 : 任意不相同的项组成的集合就称为项集 , 上述 6 个元素的集合有 2^6 个项集 ; 参考集合幂集个数
{ 奶 粉 } 是 1 项集 ;
{ 尿 布 , 啤 酒 } 是 2 项集 ;
{ 莴 苣 , 尿 布 , 啤 酒 } 是 3 项集 ;
{ 奶 粉 , 莴 苣 , 尿 布 , 啤 酒 } 是 4 项集 ;
{ 奶 粉 , 莴 苣 , 尿 布 , 啤 酒 , 甜 菜 } 是 5 项集 ;
{ 奶 粉 , 莴 苣 , 尿 布 , 啤 酒 , 甜 菜 , 橙 汁 } 是 6 项集 ;
七、关联规则 是指 :
某些 项集 出现在一个 事务 中 ,
可以推导出 :
另外一些 项集 也出现在同一个 事务 中 ;
如 : 事物 2 : t 2 = { 莴 苣 , 尿 布 , 啤 酒 , 甜 菜 }
{ 啤 酒 }1 项集 出现在购买清单 事务 2中 , { 尿 布 } 1 项集 也出现在购买清单 事务 2 中 ;
八、 数据项支持度
支持度 表示 数据项 ( Item ) 在 事务 ( Transaction ) 中的 出现频度 ;
支持度公式 :
S u p p o r t ( X ) = c o u n t ( X )/ c o u n t ( D )
S u p p o r t ( X ) 指的是 X 项集的支持度 ;
c o u n t ( X ) 指的是 数据集 D 中含有项集 X 的事务个数 ;
c o u n t ( D ) 指的是 数据集 D 的事务总数 ;
举例说明:

项集 X = { 奶 粉 } , 求该项集的支持度 ?
根据上述公式 S u p p o r t ( X ) = c o u n t ( X ) /c o u n t ( D ) 计算支持度 ;
c o u n t ( X ) 指的是 数据集 D 中含有项集 X 的事务个数 ;
含有 X = { 奶 粉 } 项集的事务有 事务 1 , 事务 3 , 事务 4 , 事务 5 , 得出 :
c o u n t ( X ) = 4
c o u n t ( D ) 指的是 数据集 D 的事务总数 ;
得出 c o u n t ( D ) = 5
则计算支持度 :
S u p p o r t ( X ) = c o u n t ( X )/ c o u n t ( D )
即:S u p p o r t ( X ) = 4 /5
九、关联规则支持度
关联规则 X ⇒ Y 的支持度 ,
等于 项集 X ∪ Y 的支持度 ;
公式为 :
S u p p o r t ( X ⇒ Y ) = S u p p o r t ( X ∪ Y ) = c o u n t ( X ∪ Y ) /c o u n t ( D )
举例说明:
求关联规则 尿 布 ⇒ 啤 酒 的支持度 ?
上述问题等价于 , 项集 X = { 尿 布 , 啤 酒 } 的支持度 ;
根据上述公式
S u p p o r t ( X ⇒ Y ) = S u p p o r t ( X ∪ Y ) = c o u n t ( X ∪ Y ) /c o u n t ( D )
计算支持度 ;
c o u n t ( X ∪ Y ) 指的是 数据集 D 中含有项集 X ∪ Y的事务个数 ;
含有 X ∪ Y = { 尿 布 , 啤 酒 } 项集的事务有 事务 2 , 事务 3 , 事务 4 , 得出 :
c o u n t ( X ∪ Y ) = 3
c o u n t ( D ) 指的是 数据集 D 的事务总数 ; 得出
c o u n t ( D ) = 5
则计算支持度 :
S u p p o r t ( X ⇒ Y ) = S u p p o r t ( X ∪ Y ) = c o u n t ( X ∪ Y ) / c o u n t ( D )
S u p p o r t ( X ) = S u p p o r t ( X ∪ Y ) = 3 / 5
十、置信度
关联规则 X ⇒ Y 的置信度 ,
表示 数据集 D 中包含 X 项集的事物 , 同时有多大可能性包含 Y 项集 ,
等于 项集 X ∪ Y 的支持度 与 项集 X 的支持度 比值 ;
公式为 :
c o n f i d e n c e ( X ⇒ Y ) = s u p p o r t ( X ∪ Y ) / s u p p o r t ( X )
举例说明:

求关联规则 尿 布 ⇒ 啤 酒 的置信度 ?
根据上述公式
c o n f i d e n c e ( X ⇒ Y ) = s u p p o r t ( X ∪ Y ) / s u p p o r t ( X )
计算 X ⇒ Y 置信度 ;
具体步骤:
1、计算 s u p p o r t ( X ∪ Y ) 支持度 :
S u p p o r t ( X ⇒ Y ) = S u p p o r t ( X ∪ Y ) = c o u n t ( X ∪ Y ) / c o u n t ( D )
s u p p o r t ( X ∪ Y ) 指的是 数据集 D 中含有项集 X ∪ Y 的事务个数 ;
含有 X ∪ Y = { 尿 布 , 啤 酒 } 项集的事务有 事务 2 , 事务 3 , 事务 4 , 得出 :
c o u n t ( X ∪ Y ) = 3
c o u n t ( D ) 指的是 数据集 D 的事务总数 , 得出
c o u n t ( D ) = 5
计算支持度结果 :
S u p p o r t ( X ⇒ Y ) = S u p p o r t ( X ∪ Y ) = c o u n t ( X ∪ Y ) / c o u n t ( D )
S u p p o r t ( X ) = S u p p o r t ( X ∪ Y ) = 3 / 5
2 、计算 S u p p o r t ( X ) 支持度 , 项集 X = { 奶 粉 } \rm X=\{ 奶粉 \} X={奶粉}
根据上述公式 S u p p o r t ( X ) = c o u n t ( X ) / c o u n t ( D ) 计算支持度 ;
c o u n t ( X ) 指的是 数据集 D 中含有项集 X 的事务个数 ;
含有 X = { 奶 粉 } 项集的事务有 事务 1 , 事务 3 , 事务 4 , 事务 5 , 得出 :
c o u n t ( X ) = 4
c o u n t ( D ) 指的是 数据集 D 的事务总数 , 得出
c o u n t ( D ) = 5
则计算支持度 :
S u p p o r t ( X ) = c o u n t ( X ) / c o u n t ( D )
S u p p o r t ( X ) = 4 / 5
3 、求最终置信度
c o n f i d e n c e ( X ⇒ Y ) = s u p p o r t ( X ∪ Y ) / s u p p o r t ( X )
c o n f i d e n c e ( X ⇒ Y ) = (3 / 5) / (4 / 5) = 3 / 4
最终置信度为 3 / 4
十一、 频繁项集
项集 X 的 支持度 s u p p o r t ( X ) , 大于等于 指定的 最小支持度阈值 minsup ,
则称该 项集 X 为 频繁项集 ,
又称为 频繁项目集 ;
十二、 非频繁项集
项集 X 的 支持度 s u p p o r t ( X ) , 小于 指定的 最小支持度阈值 minsup ,
则称该 项集 X 为 非频繁项集 ,
又称为 非频繁项目集 ;
十三、 强关联规则
项集 X 是 频繁项集 的前提下 , ( 项集 X 的 支持度 s u p p o r t ( X ) , 大于等于 指定的 最小支持度阈值 m i n s u p ) ,
置信度 c o n f i d e n c e ( X ⇒ Y ) 大于等于 置信度最小阈值 minconf ,
称该 关联规则 X⇒Y 是 强关联规则 ;
十四、 弱关联规则
项集 X 是 频繁项集 的前提下 , ( 项集 X 的 支持度 support(X) , 小于等于 指定的 最小支持度阈值 minsup ) ,
置信度 confidence(X⇒Y) 小于 置信度最小阈值 minconf ,
称该 关联规则 X⇒Y 是 弱关联规则 ;
十五、 发现关联规则
发现关联规则 :
从 数据集 D 中 , 发现支持度 support , 置信度 confidence , 大于等于给定 最小阈值 的 强关联规则 ;
目的是 发现 强关联规则 ;
十六、 非频繁项集超集性质
非频繁项集超集性质:非频繁项集 的 超集 一定是 非频繁的 ;
超集 就是 包含 该集合的集合 ;
项集 X 是 非频繁项集 , 项集 Y 是 项集 X 的超集 , 则 项集 Y 一定是 非频繁的 ;
( 说明:使用集合表示 : X ⊆ Y , X ≠ ∅ , 项集 Y 包含 项集 X , 并且 项集 X 不为空集 )
举例说明:

1 项集 {甜菜}
2 项集 {甜菜,啤酒}
上述 {甜菜,啤酒} 就是 {甜菜} 的 超集 ,
1 项集 { 甜 菜 } 其支持度是 0.2 , 小于最小支持度 minsup = 0.6 , 是 非频繁项集
那么 { 甜菜 , 啤酒 } 也是 非频繁项集 ;
在具体算法中会使用该性质 , 用于进行 “剪枝” 操作 ;
- 计算支持度时 , 按照 1 项集 支持度 , 2 项集 支持度 , ⋯ 顺序进行计算 ,
- 如果发现 1 项集 中有 非频繁项集 , 则包含该 1 项集的 n 项集 肯定是 非频繁项集 ;
- 然后使用 频繁 1 项集 组合成 2 项集 , 然后再计算这些 2 项集是否是频繁项集 ;
“剪枝” 操作 减少了不必要的计算量 ;
十七、 频繁项集子集性质
频繁项集子集性质:频繁项集 的 所有非空子集 , 一定是 频繁项集 ;
项集 Y 是 频繁项集 ,项集 Y 是 项集 X 的超集 ,则 项集 X 一定是 频繁的 ;
( 使用集合表示 : X ⊆ Y , X ≠ ∅ , 项集 Y 包含 项集 X , 并且 项集 X 不为空集 )
举例说明:

1 项集 {尿布} , {啤酒}
2 项集 {尿布,啤酒}
2 项集 {尿布,啤酒} 其支持度是 0.6 , 等于最小支持度 minsup = 0.6 , 是 频繁项集
那么 2 项集 {尿布,啤酒} 的子集是 1 项集 {尿布} , {啤酒} ,根据上述性质 , 1 项集 {尿布} , {啤酒} 都是 频繁项集 ;
十八、 项集与超集支持度性质
任意一个 项集 的 支持度 , 都 大于等于 其 超集 支持度 ;
超集 就是 包含 该集合的集合 ;
十九、 Apriori 算法过程

原始数据集 D ,
1、1 项集 C1 , 2 项集 C2 , ⋯ , k 项集 Ck , 这些项集都是候选项集 ,
2、根据 原始数据集 D , 创造 1 项集 C1 , 然后对 C1 执行 数据集扫描函数 , 找到其中的 频繁 1 项集 L1 ,
3、根据 频繁 1 项集 L1 , 创造 2 项集 C2 , 然后对 C2 执行 数据集扫描函数 , 找到其中的 频繁 2 项集 L2 ,
4、根据 频繁 k−1 项集 Lk−1 , 创造 k 项集 Ck , 然后对 Ck 执行 数据集扫描函数 , 找到其中的 频繁 k 项集 Lk ,
二十、 Apriori 算法示例 求 频繁项集
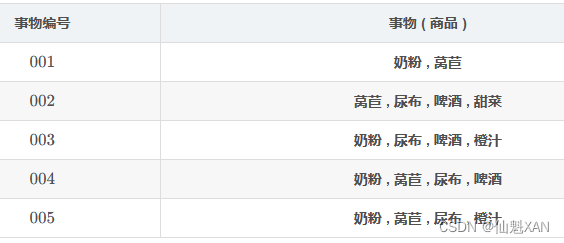
最小支持度阈值为 minsup = 0.6
1、根据 原始数据集 D , 创造 1 项集 C1 , 然后对 C1 执行 数据集扫描函数 , 找到其中的 频繁 1 项集 L1
C1 1项集
| item | sup |
| {奶粉} | 0.8 |
| {莴苣} | 0.8 |
| {尿布} | 0.8 |
| {啤酒} | 0.6 |
| {甜菜} | 0.2 |
| {橙汁} | 0.4 |
所以 L1 频繁 1 项集如下:
| item | sup |
| {奶粉} | 0.8 |
| {莴苣} | 0.8 |
| {尿布} | 0.8 |
| {啤酒} | 0.6 |
2、根据 频繁 1 项集 L1 , 创造 2 项集 C2 , 然后对 C2 执行 数据集扫描函数 , 找到其中的 频繁 2 项集 L2
C2 2 项集
| Item | Sup |
| {奶粉,莴苣} | 0.6 |
| {奶粉,尿布} | 0.6 |
| {奶粉,啤酒} | 0.4 |
| {莴苣,尿布} | 0.6 |
| {莴苣,啤酒} | 0.4 |
| {尿布,啤酒} | 0.6 |
所以 L2 频繁 2 项集
| Item | Sup |
| {奶粉,莴苣} | 0.6 |
| {奶粉,尿布} | 0.6 |
| {莴苣,尿布} | 0.6 |
| {尿布,啤酒} | 0.6 |
3、根据 频繁 2 项集 L2 , 创造 3 项集 C3 , 然后对 C3 执行 数据集扫描函数 , 找到其中的 频繁 3 项集 L3
C3 3 项集
| Item | Sup |
| {奶粉,莴苣,尿布} | 0.4 |
所以 3 项集中没有频繁项集 ;
二十一、使用 Apriori 算法,求 频繁项集 和 关联规则
如下事物数据库 , 最小支持度 60% , 最小置信度 80%
| TID | Item |
| T1 | {M,O,N,K,E,Y} |
| T2 | {D,O,N,K,E,Y} |
| T3 | {M,A,K,E} |
| T4 | {M,U,C,K,Y} |
| T5 | {C,O,O,K,I,E} |
( 1 ) 使用 Apriori 算法找出所有频繁项集 ;
( 2 ) 写出关联规则 ;
( 1 ) 使用 Apriori 算法找出所有频繁项集 ;
1)根据原始数据集 D 创造 1 项集 C1 , 如下 :
| Item | Sup |
| {M} | 60% |
| {O} | 60% |
| {N} | 40% |
| {K} | 80% |
| {E} | 80% |
| {Y} | 60% |
| {D} | 20% |
| {A} | 20% |
| {U} | 20% |
| {C} | 40% |
| {I} | 20% |
对 1 项集的C1 进行数据集扫描函数,找到频繁 1 项目集 L1,既是筛选出支持度大于等于60%的1项集,如下
| Item | Sup |
| {M} | 60% |
| {O} | 60% |
| {K} | 100% |
| {E} | 80% |
| {Y} | 60% |
2)根据频繁 1 项集 L1,创造 2 项集 C2,如下
| Item | Sup |
| {M,O} | 20% |
| {M,K} | 60% |
| {M,E} | 40% |
| {M,Y} | 40% |
| {O,K} | 60% |
| {O,E} | 60% |
| {O,Y} | 40% |
| {K,E} | 80% |
| {K,Y} | 60% |
| {E,Y} | 40% |
对 2 项集C2 进行数据集扫描函数,找到频繁 2 项集 L2,既是筛选出支持度大于等于60%的 2 项集,如下
| Item | Sup |
| {M,K} | 60% |
| {O,K} | 60% |
| {O,E} | 60% |
| {K,E} | 80% |
| {K,Y} | 60% |
3)、根据频繁 2 项集 L2 ,创造出 3 项集 C3,如下
| Item | Sup |
| {K,E,Y} | 40% |
| {O,K,E} | 60% |
对 3 项集 C3 进行数据集扫描函数,找到频繁 3 项集 L3,既是筛选出支持度大于等于60%的 3 项集,如下
| Item | Sup |
| {O,K,E} | 60% |
最终得到频繁项集有:
1)频繁 1 项集:{M},{O},{K},{E},{Y}
2)频繁 2 项集:{M,K},{O,K},{O,E},{K,E},{K,Y}
3)频繁 3 项集:{O,K,E}
(2)写出关联规则
1)基于频繁 2 项集 L2 的关联规则
| 规则 | Conf |
| M=>K | 100% |
| k=>M | 60% |
| O=>k | 100% |
| K=>O | 60% |
| O=>E | 100% |
| E=>O | 75% |
| K=>E | 80% |
| E=>K | 100% |
| K=>Y | 60% |
| Y=>K | 100% |
2)基于 频繁 3 项集 L3 的关联规则
| 规则 | Conf |
| O=>K,E | 100% |
| K,E=>O | 75% |
| K=>O,E | 60% |
| O,E=>K | 100% |
| E=>O,K | 75% |
| O,K=>E | 100% |
所以,根据置信度大于等于 80% 的关联规则有:
L2 关联规则:M=>k,O=>k,O=>E,K=>E,E=>K,Y=>K
L3 关联规则:O=>K,E、 O,E=>K、O,K=>E
参考文献
https://hanshuliang.blog.csdn.net/article/details/109687195
【数据挖掘】数据挖掘总结 ( 模式挖掘 | Apriori 算法 | 支持度 | 置信度 | 关联规则 ) ★★_模式挖掘 置信
【数据挖掘】关联规则挖掘 Apriori 算法 ( 关联规则 | 数据项支持度 | 关联规则支持度 )_关联规则支持度计算公式
【数据挖掘】关联规则挖掘 Apriori 算法 ( 频繁项集 | 非频繁项集 | 强关联规则 | 弱关联规则 | 发现关联规则 )_支持度可信度频繁项集非频繁项集


