堆排序算法_由数组转化为堆的过程

一、大顶堆和小顶堆概念

        堆排序是利用堆数据结构而设计的一种排序算法，堆排序是一种选择排序，其最坏，最好，平均时间复杂度均为O(nlogn)，同时也是不稳定排序。
堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆, 如下图所示，其中大顶堆的性质：arr[i] >= arr[2i] && arr[i] >= arr[2i+1]

 

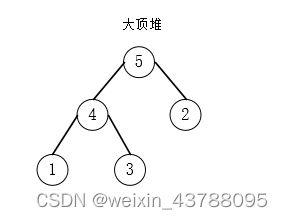
每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆，如下图所示，其中小顶堆性质：arr[i] <= arr[2i] && arr[i] <= arr[2i+1]

二、堆排序的基本思想

（1）将无序序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;
（2）将堆顶元素与末尾元素交换，将最大元素放到数组末端;
（3）重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整和           交换步骤，直到整个序列有序。 

举例：

1、将无序序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆
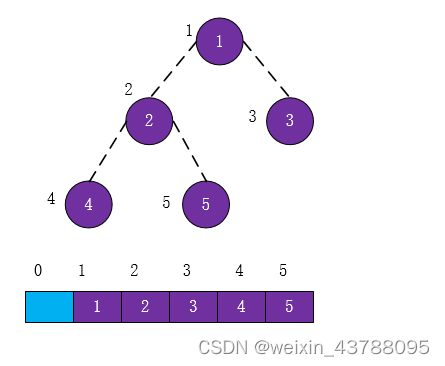
（1）假设给定无序序列结构如下：

  

 2、此时从数组的一半处开始进行调整（数组的0号位不存数，因此数组实际长度要减1），即从2号位开始调整。

（1）让root指向2号结点，让child=2*root即指向4号结点；

（2）判断child + 1 <= length && list->data[child] < list->data[child + 1]，即取左右孩子结点中的较大的一个；

（3）若满足条件则右孩子结点的值大，取右孩子（child++）；否则取左孩子（child）；因为1<4，所有取右孩子（child=5）

（4）找到左右孩子结点的较大者后与其父节点（root=2）进行比较，若child所指结点的值大于root所指结点的值则需要将两个结点的值进行互换，否则不需要进行值的互换；因为list->data[root] >= list->data[child]，所以不需要进行值的互换

（5）让root=child，若2*root<=length，则在进行上述操作进行调整；否则进行下一个结点的调整即3

（6）将2号位调整完成后，堆的形状和数组中的内容如下图所示

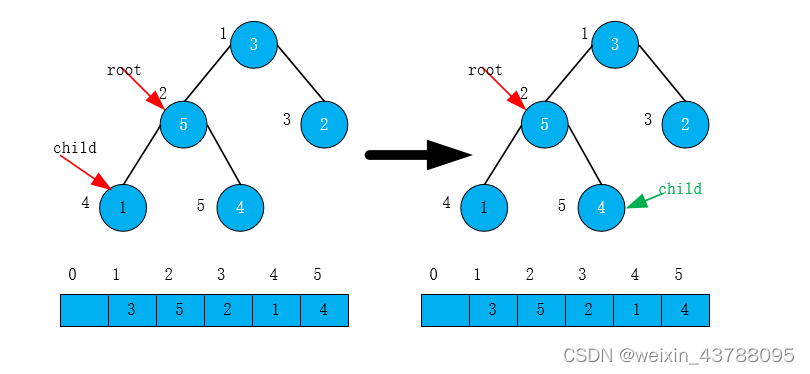
3、从1号结点开始调整

（1）root指向1号结点，child=2*root指向2号结点

（2）判断child + 1 <= length && list->data[child] < list->data[child + 1]，即取左右孩子结点中的较大的一个；

（3）若满足条件则右孩子结点的值大，取右孩子（child++）；否则取左孩子（child）；因为5>2，所有取左孩子（child=2）

（4）找到左右孩子结点的较大者后与其父节点（root=1）进行比较，若child所指结点的值大于root所指结点的值则需要将两个结点的值进行互换，否则不需要进行值的互换；因为list->data[root] <= list->data[child]，所以需要进行值的互换

（5）让root=child，若2*root<=length，则在进行上述操作进行调整；否则进行下一个结点的调整，

（6）经过该轮调整后结果如下图所示

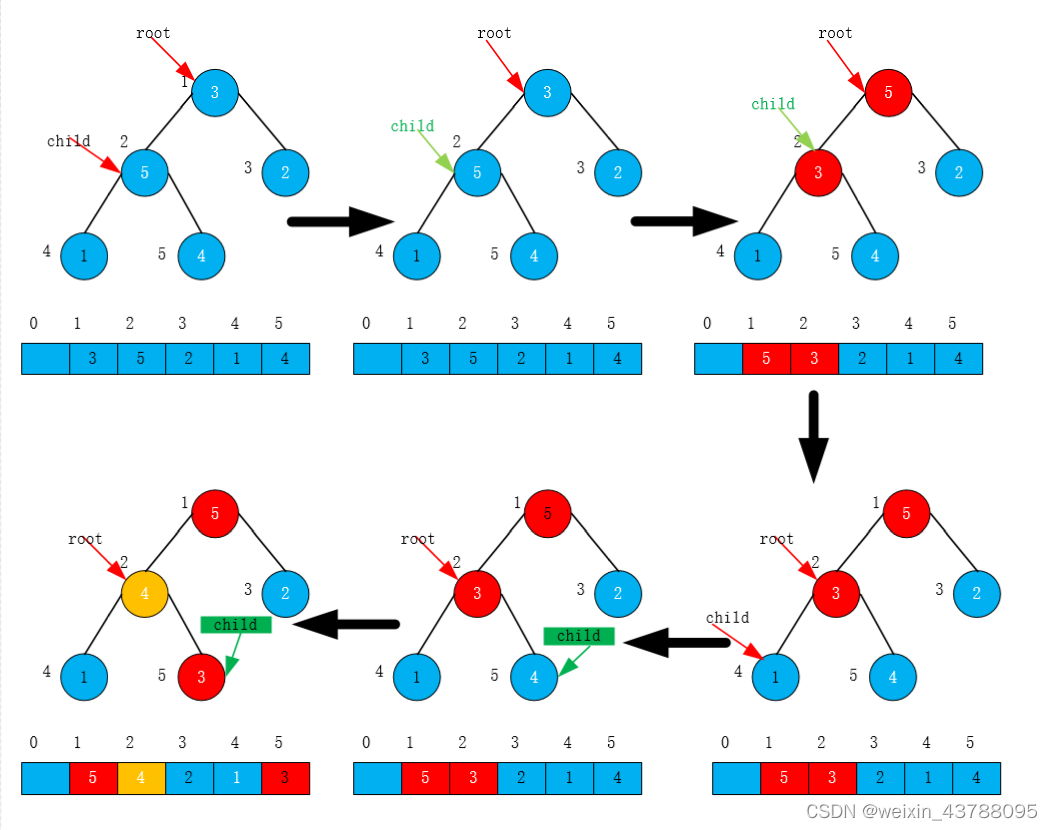
 4、将第一个结点与最后一个结点值进行互换

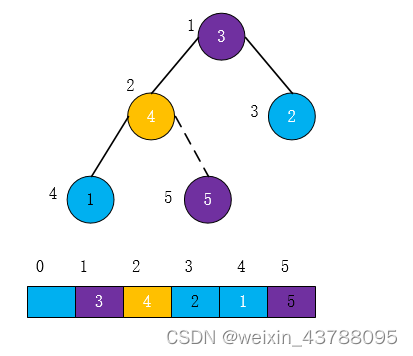
 5、再从length-1个长度重复以上操作，继续进行调整，交换，如此反复进行，最终使得整个序列有序

三、代码实现

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <math.h>
#include <time.h>
#include <Windows.h>
 
#define MAXSIZE 20
typedef int DATATYPE;
 
typedef struct seqList
{
	DATATYPE data[MAXSIZE];
	int length;
}SeqList;
//初始化顺序表
void InitSeqList(SeqList* list)
{
	for (int i = 0; i < MAXSIZE; i++)
	{
		list->data[i] = 0;
	}
	list->length = 0;
}
//创建顺序表
void CreateSeqList(SeqList* list)
{
	DATATYPE data, length;
	printf("请输入要创建的顺序表的长度：");
	scanf_s("%d", &length);
	printf("请输入数据：");
	for (int i = 1; i <= length; i++)
	{
		scanf_s("%d", &data);
		list->data[i] = data;
		list->length++;
	}
}
//堆排序调整过程
void AdjustHeap(SeqList* list, int root, int length)//root表示要开始调整的结点
{
	list->data[0] = list->data[root];//先保存要调整结点
	int child = 0, temp = 0;
	for (;2 * root <= length;root = child)
	{
		child = 2 * root;//左孩子
		if (child + 1 <= length && list->data[child] < list->data[child + 1])//取左右孩子中较大一个
			child++;
		if (list->data[0] >= list->data[child])//若已经是大顶堆不需要调整
			break;
		else
		{
			list->data[root] = list->data[child];//调整堆使根节点为最大的
			list->data[child] = list->data[0];
		}
	}
}
void swap(int* a, int* b)
{
	int temp = 0;
	temp = *a;
	*a = *b;
	*b = temp;
}
//堆排序
void HeapSort(SeqList* list, int length)
{
	int i, j;
	for (i = length / 2; i >= 1; i--)//从一半结点处开始调整堆
	{
		AdjustHeap(list, i, length);
	}
	for (j = length; j >= 1; j--)
	{
		swap(&list->data[j], &list->data[1]);//将堆顶元素与最后一个元素互换
		AdjustHeap(list, 1, j - 1);//在调整
	}
}
 
//打印
void PrintfSeqList(SeqList* list)
{
	for (int i = 1; i <= list->length; i++)
	{
		printf("%6d", list->data[i]);
	}
	printf("\n");
}
int main(void)
{
	SeqList list;
	
 
	//堆排序
	printf("--------------------堆排序--------------------\n");
	InitSeqList(&list);
	CreateSeqList(&list);
	PrintfSeqList(&list);
	HeapSort(&list,list.length);
	printf("堆排序得到的排序序列为：");
	PrintfSeqList(&list);
	
 
	system("pause");
	return EXIT_SUCCESS;
}