协同过滤 —— Collaborative Filtering
协同过滤简单来说就是根据目标用户的行为特征,为他发现一个兴趣相投、拥有共同经验的群体,然后根据群体的喜好来为目标用户过滤可能感兴趣的内容。
协同过滤推荐 —— Collaborative Filtering Recommend
协同过滤推荐是基于一组喜好相同的用户进行推荐。它是基于这样的一种假设:为一用户找到他真正感兴趣的内容的最好方法是首先找到与此用户有相似喜好的其他用户,然后将他们所喜好的内容推荐给用户。这与现实生活中的“口碑传播(word-of-mouth)”颇为类似。
协同过滤推荐分为三类:
- 基于用户的推荐(User-based Recommendation)
- 基于项目的推荐(Item-based Recommendation)
- 基于模型的推荐(Model-based Recommendation)
基于用户的协同过滤推荐 —— User CF
原理:基于用户对物品的喜好找到相似邻居用户,然后将邻居用户喜欢的物品推荐给目标用户
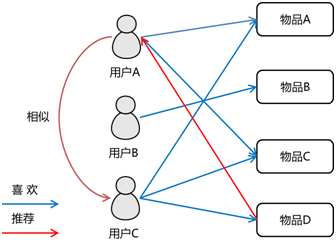
实现:将一个用户对所有物品的偏好作为一个向量(Vector)来计算用户之间的相似度,找到K-邻居后,根据邻居的相似度权重以及他们对物品的喜好,为目标用户生成一个排序的物品列表作为推荐,列表里面都是目标用户为涉及的物品。
基于物品的协同过滤推荐 —— Item CF
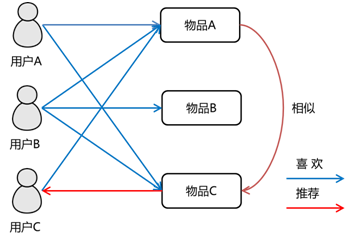
实现:将所有用户对某一个物品的喜好作为一个向量来计算物品之间的相似度,得到物品的相似物品后,根据用户历史的喜好预测目标用户还没有涉及的物品,计算得到一个排序的物品列表作为推荐。
相似度的计算 —— Similarity Metrics Computing
- 欧几里德距离(Euclidean Distance)

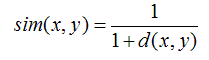
- 皮尔森相关系数(Pearson Correlation Coefficient)

- Cosine 相似度(Cosine Similarity)
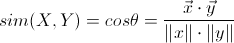
相似邻居的计算
- 固定数量的邻居:K-neighborhoods 或者 Fix-size neighborhoods
- 基于相似度门槛的邻居:Threshold-based neighborhoods

1. 基于皮尔森相关性的相似度 —— Pearson correlation-based similarity
皮尔森相关系数反应了两个变量之间的线性相关程度,它的取值在[-1, 1]之间。当两个变量的线性关系增强时,相关系数趋于1或-1;当一个变量增大,另一个变量也增大时,表明它们之间是正相关的,相关系数大于0;如果一个变量增大,另一个变量却减小,表明它们之间是负相关的,相关系数小于0;如果相关系数等于0,表明它们之间不存在线性相关关系。
用数学公式表示,皮尔森相关系数等于两个变量的协方差除于两个变量的标准差。
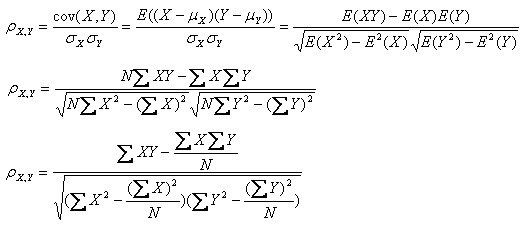
协方差(Covariance):在概率论和统计学中用于衡量两个变量的总体误差。如果两个变量的变化趋于一致,也就是说如果其中一个大于自身的期望值,另一个也大于自身的期望值,那么两个变量之间的协方差就是正值;如果两个变量的变化趋势相反,则协方差为负值。
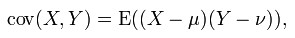
标准差(Standard Deviation):标准差是方差的平方根
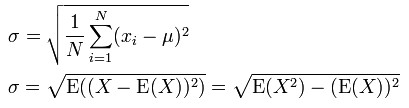
方差(Variance):在概率论和统计学中,一个随机变量的方差表述的是它的离散程度,也就是该变量与期望值的距离
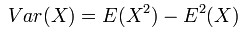
基于皮尔森相关系数的相似度有两个缺点:

同样的场景在现实生活中也经常发生,比如两个用户共同观看了200部电影,虽然不一定给出相同或完全相近的评分,他们之间的相似度也应该比另一位只观看了2部相同电影的相似度高吧!但事实并不如此,如果对这两部电影,两个用户给出的相似度相同或很相近,通过皮尔森相关性计算出的相似度会明显大于观看了相同的200部电影的用户之间的相似度。
2. 基于欧几里德距离的相似度 —— Euclidean Distance-based Similarity
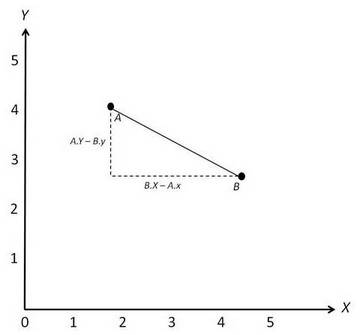
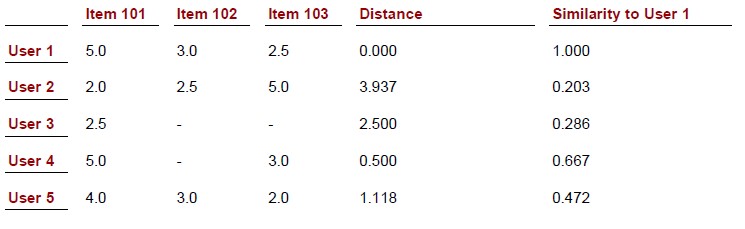

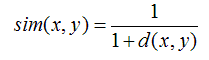
只要至少有一个共同评分项,就能用欧几里德距离计算相似度;如果没有共同评分项,那么欧几里德距离也就失去了作用。其实照常理理解,如果没有共同评分项,那么意味着这两个用户或物品根本不相似。
3. 余弦相似度 —— Cosine Similarity
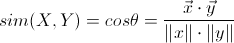
与欧几里德距离类似,基于余弦相似度的计算方法也是把用户的喜好作为n-维坐标系中的一个点,通过连接这个点与坐标系的原点构成一条直线(向量),两个用户之间的相似度值就是两条直线(向量)间夹角的余弦值。因为连接代表用户评分的点与原点的直线都会相交于原点,夹角越小代表两个用户越相似,夹角越大代表两个用户的相似度越小。同时在三角系数中,角的余弦值是在[-1, 1]之间的,0度角的余弦值是1,180角的余弦值是-1。
借助三维坐标系来看下欧氏距离和余弦相似度的区别:
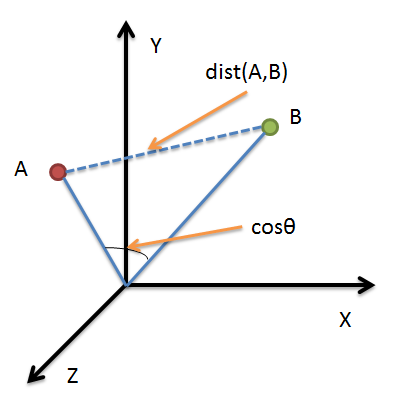
从图上可以看出距离度量衡量的是空间各点间的绝对距离,跟各个点所在的位置坐标(即个体特征维度的数值)直接相关;而余弦相似度衡量的是空间向量的夹角,更加的是体现在方向上的差异,而不是位置。如果保持A点的位置不变,B点朝原方向远离坐标轴原点,那么这个时候余弦相似度cosθ是保持不变的,因为夹角不变,而A、B两点的距离显然在发生改变,这就是欧氏距离和余弦相似度的不同之处。
根据欧氏距离和余弦相似度各自的计算方式和衡量特征,分别适用于不同的数据分析模型:欧氏距离能够体现个体数值特征的绝对差异,所以更多的用于需要从维度的数值大小中体现差异的分析,如使用用户行为指标分析用户价值的相似度或差异;而余弦相似度更多的是从方向上区分差异,而对绝对的数值不敏感,更多的用于使用用户对内容评分来区分用户兴趣的相似度和差异,同时修正了用户间可能存在的度量标准不统一的问题(因为余弦相似度对绝对数值不敏感)。
4. 调整余弦相似度 —— Adjusted Cosine Similarity
5. 斯皮尔曼相关 —— Spearman Correlation
斯皮尔曼相关性可以理解为是排列后(Rank)用户喜好值之间的Pearson相关度。《Mahout in Action》中有这样的解释:假设对于每个用户,我们找到他最不喜欢的物品,重写他的评分值为“1”;然后找到下一个最不喜欢的物品,重写评分值为“2”,依此类推。然后我们对这些转换后的值求Pearson相关系数,这就是Spearman相关系数。
斯皮尔曼相关度的计算舍弃了一些重要信息,即真实的评分值。但它保留了用户喜好值的本质特性——排序(ordering),它是建立在排序(或等级,Rank)的基础上计算的。
回顾前面表中User1~5对Item101~103的喜好(评分)值,通过斯皮尔曼相关系数计算出的相似度为:

我们发现,计算出来的相似度值要么是1,要么是-1,因为这依赖于用户的喜好值和User1的喜好值是否趋于“一致变化”还是呈“相反趋势变化"。
因为斯皮尔曼相关性的计算需要花时间计算并存储喜好值的一个排序(Ranks),具体时间取决于数据的数量级大小。正因为这样,斯皮尔曼相关系数一般用于学术研究或者是小规模的计算。
6. 基于谷本系数的相似性度量 —— Tanimoto Coefficient-based Similarity
更准确的说法为:Tanimoto Coefficient主要用于计算符号度量或布尔值度量的个体间的相似度,因为个体的特征属性都是由符号度量或者布尔值标识,因此无法衡量差异具体值的大小,只能获得“是否相同”这个结果,所以Tanimoto Coefficient只关心个体间共同具有的特征是否一致这个问题。Tanimoto Coefficient又被叫做Jaccard Coefficient,其值等于两个用户共同关联(不管喜欢还是不喜欢)的物品数量除于两个用户分别关联的所有物品数量。
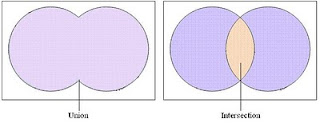
也就是关联的交集除于关联的并集,用公式表示为:

推荐中的协同过滤算法简单说明下(来自http://my.oschina.net/BreathL/blog/62519):
首先,通过分析用户的偏好行为,来挖掘出里面物品与物品、或人与人之间的关联。
其次,通过对这些关联的关系做一定的运算,得出人与物品间喜欢程度的猜测,即推荐值。
最后,将推荐值高的物品推送给特定的人,以完成一次推荐。
这里只是笼统的介绍下,方便下边的理解,IBM的一篇博客对其原理讲解得浅显易懂,同时也很详细《深入推荐引擎相关算法 - 协同过滤》,我这里就不细讲了。
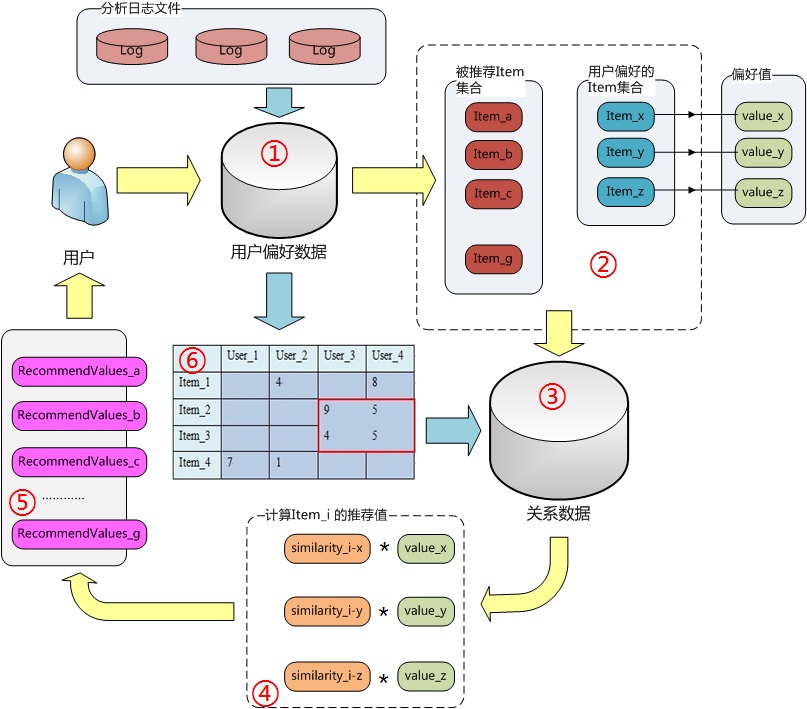
协同过滤算法大致可分为两类,基于物品的与基于用户的;区分很简单,根据上面的逻辑,若你挖掘的关系是物品与物品间的,就是基于物品的协同过滤算法,若你挖掘的关系是用户与用户间的,就是基于用户的协同过滤算法;由于它们实现是有所不同,所以我分开整理,先来看看基于物品的协同过滤实现,我自己画了一幅图:
我通过数字的顺序,来标示数据变化的方向(由小到大);下面分析下每一个步骤的功能以及实现。
首先,说明下两个大的数据源,用户偏好数据:UserID、ItemID、Preference:表示一个对一个物品的喜好程度;关系数据:ItemIDA(UserIDA)、ItemIDB(UserIDB)、Similarity:表示两个人或物品间的相似程度;接着一个用户来了,我们需要为其推荐,得拿到他的身份标示,一般是UserID,于是:
①. 查找这个用户喜欢过的物品(即偏好的产品,并查出偏好值后面会用),以及还没有喜欢过的商品,前者是推荐运算的根据,后者作为一个产生推荐的一个集合;如② 画的那样。
②. 这里是一个可扩展的地方(我自己理解);因为这两部分的数据的作用非常明显,修改这两个集合对后面产生的推荐结果可产生非常直观的影响,比如清洗过滤,或根据用户属性缩小集合;不仅使后面推荐效果更优,运算性能也可以大幅度提高。
③. 查找这两个集合之间的关系,这是一对多的关系:一个没有偏好过的物品与该用户所有偏好过的物品间的关系,有一个值来衡量这个关系叫相似度Similarity;这个关系怎么来的,看蓝色箭头的指向。步骤⑥
④. 得到这个一对多的关系后,就可以计算这个物品对于这个用户的推荐值了,图中similarity_i-x表示Item_i 与 Item_x 之间的相似度,Item_x是该用户偏好过得,该用户对其偏好值记为 value_x ,相乘;Item_i 与 该用户偏好过的所有物品以此做以上运算后,得到的值取平均值 便是 Item_i的推荐值了。注:有可能Item_i 不是与所有 该用户偏好过的物品都都存在相似性,不存在的,不计算即可;另外这里方便理解介绍的都是最简单的实现;你也可以考一些复杂的数学元素,比如方差来判断离散性等。
⑤. 这步就简单多了,刚才对该用户没有偏好过的集合中的所有Item都计算了推荐值,这里就会得到一个list,按推荐值由大到小排序,返回前面的一个子集即可。
⑥。 前面已经提到,关系数据时怎么来的,也是根据用户的偏好数据;你把其看成一个矩阵,横着看过来,参考两个Item间的共同用户,以及共同用户的偏好的值的接近度;这里的可选择的相似度算法很多,不一一介绍了,前面提到的IBM博客也详细讲解了。
基于物品的协同过滤算法分析完了,下面是基于用户的协同过滤算法,还是自己画了一幅图:
①. 同样也是查询,只是查询的对象不一样了,查询的是与该用户相似的用户,所以一来直接查了关系数据源。以及相似用户与该用户的相似度。
②. 与刚才类似,也是对数据集的一个优化,不过作用可能没那么大。(个人感觉)
③. 查询关系数据源,得到相似用户即邻居偏好过的物品;如步骤④;图中由于空间小,没有把所有邻居的偏好关系都列出来,用……表示。其次还要得到该用户偏好过的物品集合。
④. 被推荐的Item集合是由该用户的所有邻居的偏好过的物品的并集,同时再去掉该用户自己偏好过的物品。作用就是得到你的相似用户喜欢的物品,而你还没喜欢过的。
⑤. 集合优化同基于物品的协同过滤算法的步骤②。
⑥. 也是对应类似的,依次计算被推荐集合中Item_i 的推荐值,计算的方式略有不同,Value_1_i表示邻居1对,Item_i的偏好值,乘以该用户与邻居1的相似度 Similarity1;若某个邻居对Item_i偏好过,就重复上述运算,然后取平均值;得到Item_i的推荐值。
⑦、⑧. 与上一个算法的最后两部完全类似,只是步骤 ⑧你竖着看,判断两个用户相似的法子和判断两个物品相似的法子一样。