PID算法的原理及各个环节作用说明及应用_pid算法详解与作用

一、PID的原理介绍

发展历史

1、1932年美国的奈奎斯特（H.Nyquist）发表了一篇采用图形的方法来判断系统的稳定性的论文；
2、在奈奎斯特的工作基础上，伯德（H.W.Bode）等人建立了一套在频域范围设计反馈放大器的方法。
3、后来，反馈控制原理开始应用于工业过程中，在1936年英国的考伦德（A.Callender）和斯蒂文森（A.Stevenson）等人正式给出了PID控制方法。
参考资料链接
PID发展史
注：
PID算法分为比例（Proportional）、积分（Integral）、微分（Differential）三个部分，其输入是期望值（也叫参考值或目标值）与系统输出的实际值的差。在PID算法还没有被正式提出时，其中比例环节已经被应用，只是没有给出正式的名字而已，比如用杯子接水时，人脑就可以看成是一个比例控制环节，整个过程如下：
（1）人眼是传感器，不断接收杯口位置于杯内水位的差"err"输入到人脑；
（2）人脑通过误差值"err"来控制手去调节控水阀门开合的大小，“err”<0,且越小，阀门开的越大，随着“err”->‘0’，阀门就开的越小直至关闭。

公式推导及原理说明

1、公式推导（公式编辑器还不太会，后续补上）
1.1 PID连续形式：

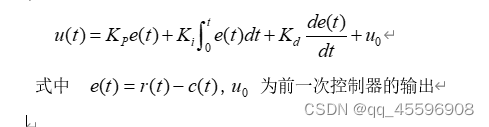
其中r(t)为参考值，c(t)为系统输出实际值。
1.2 PID离散形式：

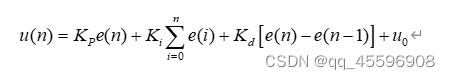
注意：这里给出的两种PID控制公式形式是经过简化的，与其它地方给出的公式中系数不太一样，这是为了便于理解，控制原理及过程都是一致的。
**错误纠正：**上述PID形式为位置式PID，不应该有u0
2、原理说明
2.1 控制的目的
对某一系统施加控制，其目的一定是想让系统从某一状态到达所期望的状态，比如人在驯服动物时，对动物施加的一系列行为，目的是想让动物从最初的不听命令的态度转变为服从人的命令的态度。
2.2 PID的原理
从公式可以看到，PID控制器有一个系统输出c(t)的反馈，所以PID是一个反馈控制器，通过参考值与反馈值的差“err”，输入到PID控制器，会得到一个输出，将输出作用于系统。下面举一个给水壶加热的例子，来说明PID输出是怎么控制系统的。

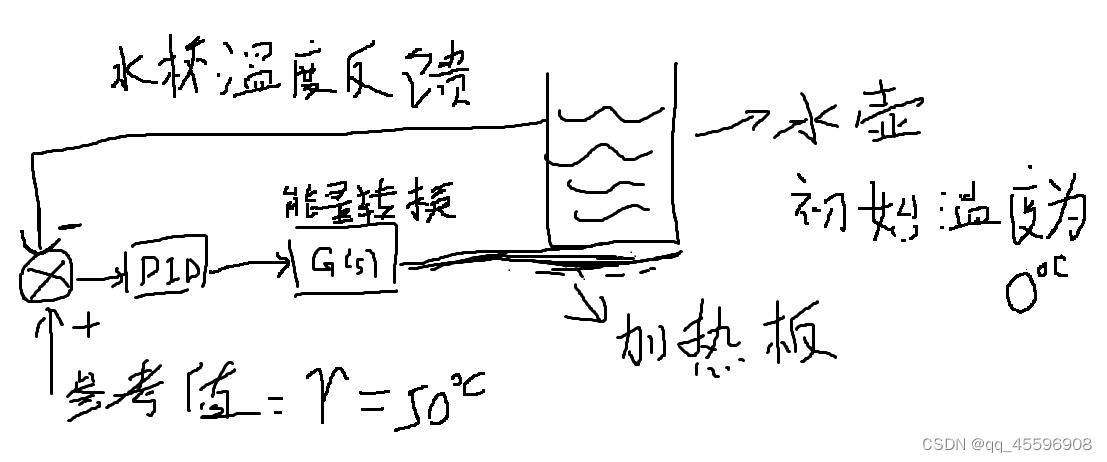
上图为用PID控制加热水壶例子示意图，其中最左边的圆圈中带一个’ב符号计算每次参考值和反馈值的温度差值’err‘，然后输入PID控制器，PID控制器的输出给到一个加热器的能量转换模块，这一部分是由传感器和各种元器件构成，在实际的应用中需要考虑。
整个系统中PID控制流程为： 刚开始，差值’err‘很大，所以PID输出也会很大，能量转换模块给的能量输出也会很大，随着水壶中温度上升，差值’err‘逐渐减小，PID控制器的输出也会减小，能量转换模块的能量输出也会减小。

三个环节的作用

1 比例环节（比例控制）
比例环节就像它的名字一样，一个比例系数乘以误差值’err‘，来调节系统的输出，下面先不考虑控制系统的能量转换模块，就只考虑用比例环节来进行系统的初始值到期望值的调节，如下图所示，期望值V设的50，比例系数Kp为0.03，积分系数和微分系数为Ki，Kd，其结果如下

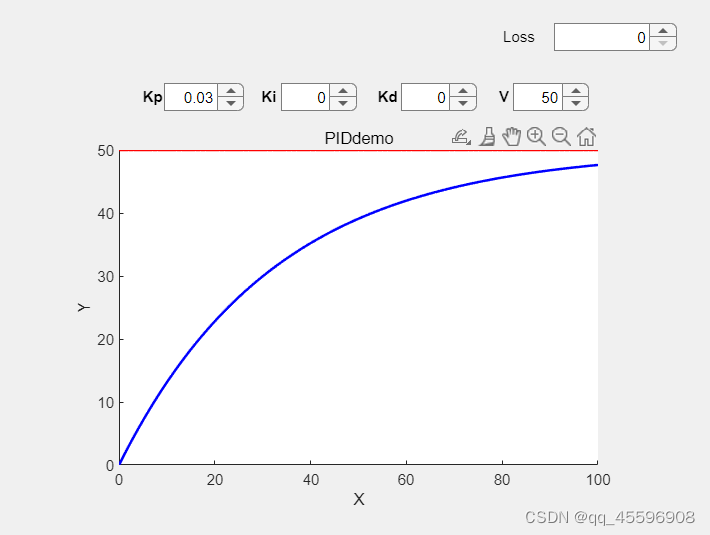
增大比例系数Kp，系统到达期望值的时间越快（响应速度更快），设Kp为0.2，结果如下

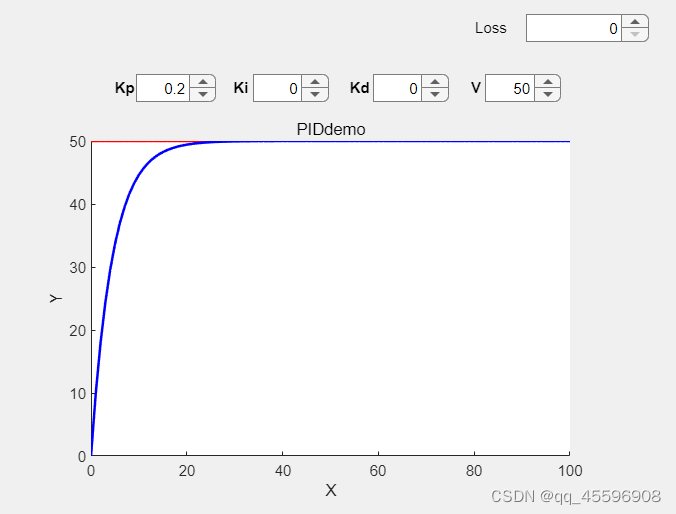
可以明显看到，响应速度更快了。
2 积分环节（积分控制）
在大多数资料上写的都是积分环节的作用是消除系统的稳态误差，它的作用的确是这样的。
但是这里关键的是要理解什么是稳态误差？造成稳态误差的原因是什么？“稳态误差”可以理解为系统期望状态与系统达到某个平衡状态（稳定状态）时的差值。“造成稳态误差的原因”是现实世界中客观存在的规律，如在上述加热水壶的过程中，我们并没有考虑在每次加热时，水壶的热量散失的情况，现在考虑水壶加热过程有热量散失的情况，还是只用比例环节来控制，设置比例系数Kp为0.2，Ki和Kd为0，水壶从0℃加到50℃，每次控制器输出加热时，散失的热量让水壶温度下降1℃，这里假设水壶被加热到45℃，此时误差’err’为5℃，控制器u='err’×Kp=1，所以给水壶加热1℃，因为每加热一次就会损失1℃，故在只有比例控制下，考虑水壶散热情况（在实际中是必然存在的），水壶只能被加热到45℃。因此这里引入积分环节，对每一次的误差进行累加，当系统处于稳态且有稳态误差时，可以增大系统的输入量以达到消除稳态误差的效果。

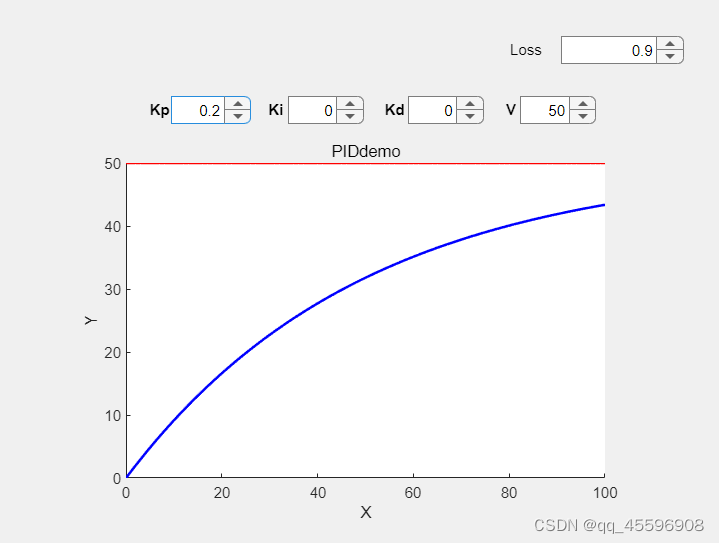
图片中右上角的’loss’数值代表的是每次控制器输出u，都会损失掉 loss×u 的量。可以看到考虑损失量时，系统就会存在稳态误差。现在令Ki=0.001,结果如下：

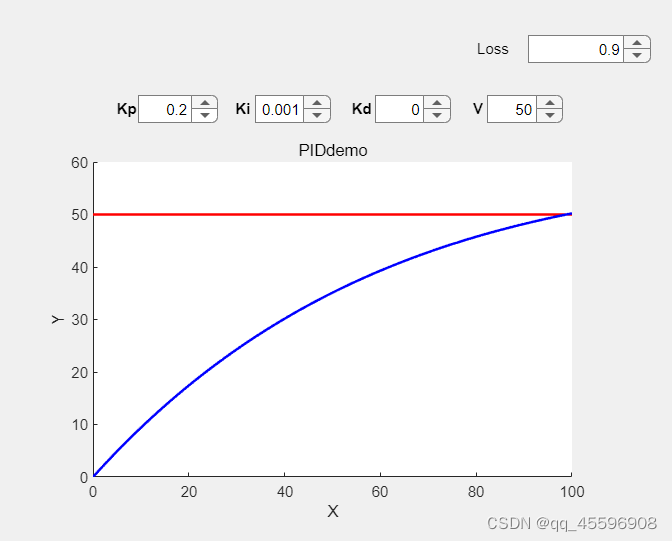
可以看到，系统可以达到期望值。
3 微分环节（微分控制）
微分环节在很多资料中都有不同的解释，但是最终想表达的意思都是一致的。这里我把微分环节理解为一个惯性环节，下面具体说一下为什么这么理解，举两个例子。

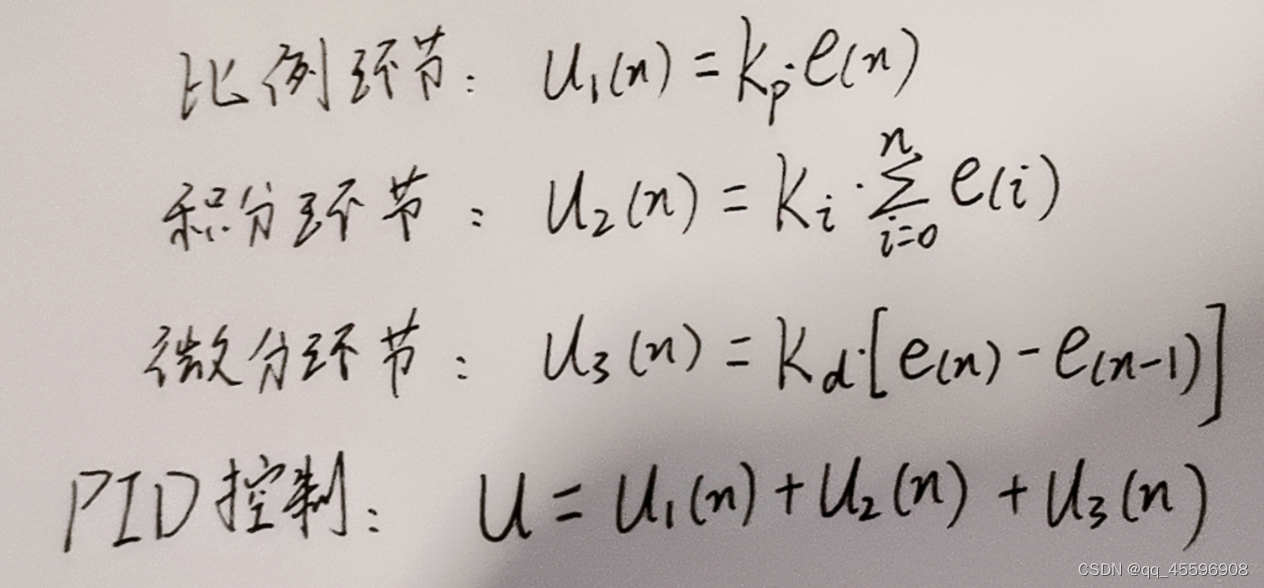
（1）加热水壶的例子
水壶初始温度为0℃，期望温度为50℃，
第一种情况，当温度往上涨，err(n)为第n次误差，err(n-1)为第n-1次误差，每一次 err(n)小于err(n-1)，即 [err(n)-err(n-1)]<0，如上图公式可以看到，微分环节u3始终为负，所以起到一个阻碍温度增加的作用。加入微分环节的作用是在水壶快要到达期望温度时，能够较为平缓的到达，降低出现超过期望值的情况（减少震荡）。
第二种情况，当水壶温度值超过期望值，未达到峰值时，err(n) < 0 , err(n-1) < 0，且err(n) < err(n-1)，所以[err(n)-err(n-1)]<0，即微分环节依然是在阻碍温度增加（此时比例环节和积分环节也是在阻碍温度增加）。
第三种情况，当温度上涨到峰值开始下降，且未降到期望温度时，此时err(n) < 0 , err(n-1) < 0，且err(n) > err(n-1)，所以[err(n)-err(n-1)]>0，微分环节为正，起到阻碍温度下降的作用（比例环节和积分环节促进温度降低作用）。
从上述三种情况可以看到，微分环节的作用，其实就是像惯性一样，它具有一个维持系统保持原有状态的能力，从水壶加热的过程可以看到，当水壶温度上升到超过期望值，到达峰值，然后温度下降的过程，水壶的温度曲线就在期望温度值上下震荡，通过微分环节的惯性作用，可以减小曲线的震荡。
（2）汽车刹车例子
正常情况下，汽车在路口看到红灯时，要做减速，停在路口，等绿灯后通行。当汽车快到达路口时，假设汽车从速度10m\s做减速运动到速度为0，在这个过程，初始状态为汽车速度10m\s，期望状态为汽车速度0 m\s，此时err(n) < 0 , err(n-1) < 0，且err(n) > err(n-1)，所以[err(n)-err(n-1)]>0，比例环节和积分环节都是在促进汽车制动，而微分环节是在阻碍汽车制动（像前面说的，微分环节具有惯性作用，会维持系统本来的状态），在刹车过程中，微分环节的作用可以理解为，让汽车在刹车的过程变得平缓，避免出现急踩刹车的情况。

二、PID的应用介绍

PID实际应用中说明（根据自己碰到问题的总结）

网上资料以及其它的一些资料中，关于PID的学习资料基本都没有考虑在实际应用中涉及到的控制系统中各种能量转换的情况，比如在大多数的PID学习资料中，都是规定某个系统的初始值和期望值，然后用PID算法进行调节，把初始值调到期望值。但是在实际的系统里，并不是这么简单的，这中间会涉及到各种传感器和能量的转换，比如控制小车速度，这需要编码器测到电机的转速，然后转换成电压值来进行PID的控制，并不是简单的直接控制小车速度。
所以将PID应用于实际的系统中时，要分析哪些是系统的被控量和控制量。怎么去分辨被控量和控制量，被控量是自动控制系统的输出（也被称为输出量，即被控对象中的物理量），控制量是自动控制系统中执行机构中的物理量。举一个例子，例如电风扇，其中被控量是风扇的风力大小或是风速，可以通过人为的调节风力的级别（一档位、二档位等），也就是系统控制的期望值，控制量是电风扇中电机的转速，被控对象就是电风扇，可以将电风扇的控制过程简化成如下：当设定风扇风速档位后（期望值，是以某个值的电压或电流形式），传感器会检测风扇的转速（被控量），将其转化成相应大小的电压或电流信号传给变送器，然后传给控制器，控制器通过期望值与风扇的实际值相比较，得出一个输出作用于电风扇的电机上，来调节电机的转速（控制量），进而让风扇的风力到达期望值。
注：
上述是自己学习过程的一些理解，有很多不严谨和不对的地方，欢迎读者进行批评指正。

三、文中用到的PID系数调节模块

阿里网盘链接

百度网盘链接
提取码：1111