导数的概念——“高等数学”_导数 高数
赞
踩
各位CSDN的uu们你们好呀，今天小雅兰的内容是导数的概念，其实在高中时期，我们就已经接触过导数了，但是那个时候学得并不是特别深入，依稀记得，我们当初的导数大题一般都是压轴题，很多学校每次讲解试卷时都只会讲解第一问，只有确信在我们能力范围之内的，才会讲解后面的第二三小问，好了，话不多说，我们一起进入导数的世界吧
一、引例
二、导数的定义
三、导数的几何意义
四、可导与连续的关系
一、引例
其实这种变化率问题我们高中就已经学过，我们只是来回顾一下
下面我们来看一下更复杂的变化率问题
我们学物理的同学应该知道这个问题
如果M点靠M0点足够地近，或者t时刻离t0时刻足够地近，那么这个平均速度就越能接近于M0或者t0时刻的瞬时速度，但是不管怎么近似，终归是一个近似的瞬时速度
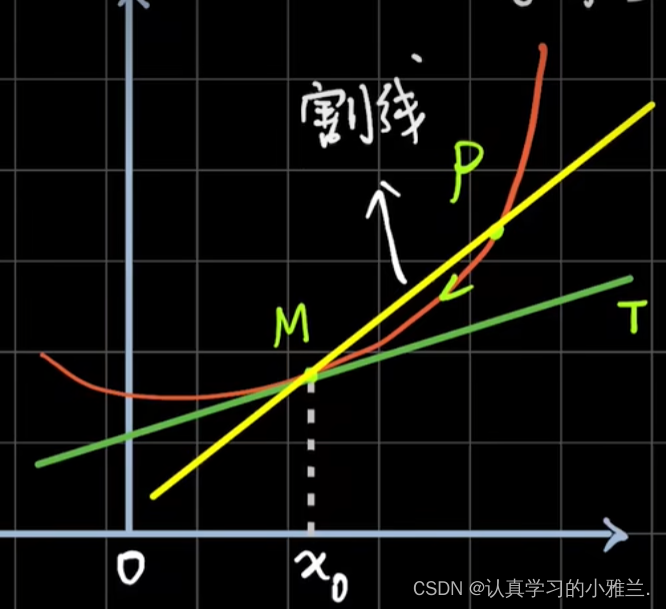
割线的极限为切线
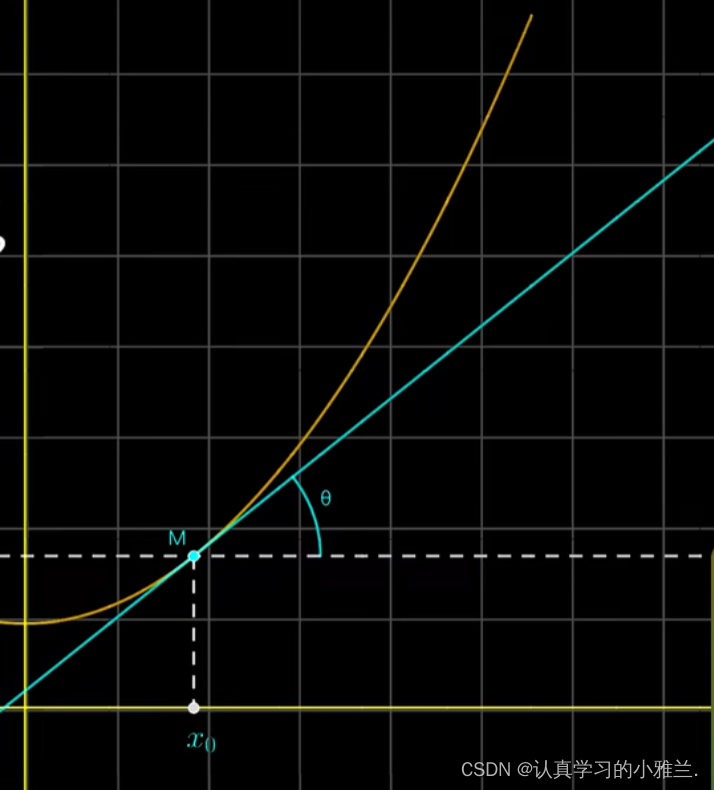
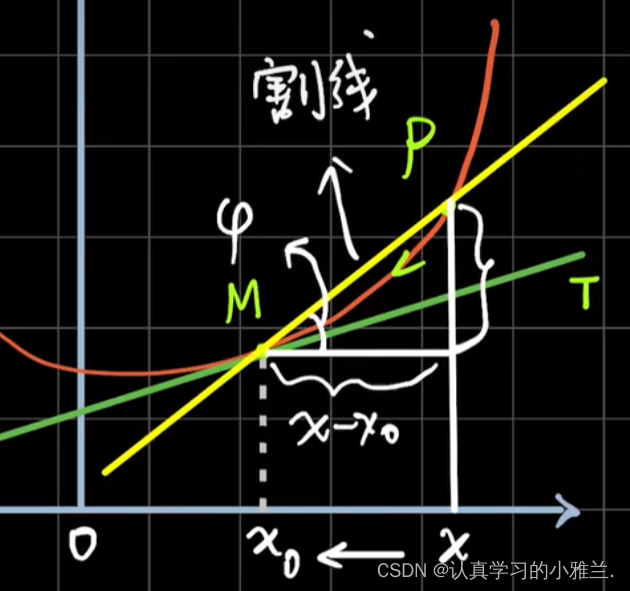
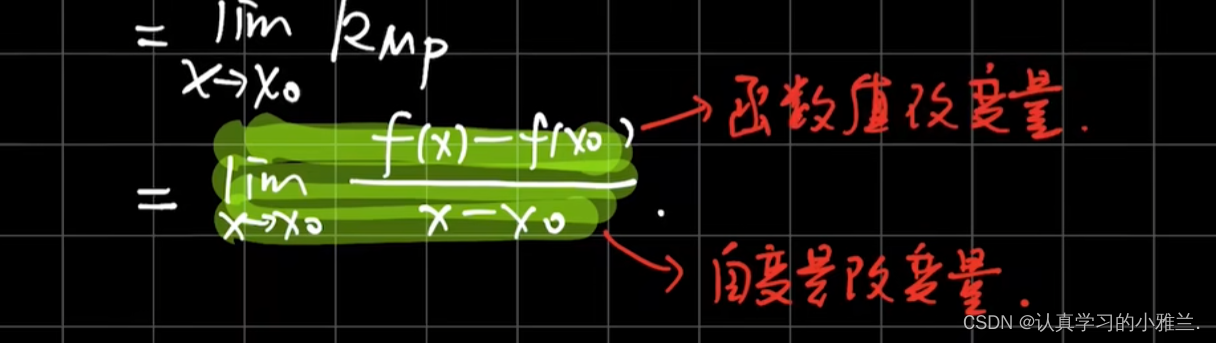
二、导数的定义
导数（Derivative）是微积分中的重要基础概念。当自变量的增量趋于零时，因变量的增量与自变量的增量之商的极限。在一个函数存在导数时，称这个函数可导或者可微分。可导的函数一定连续。不连续的函数一定不可导。导数实质上就是一个求极限的过程，导数的四则运算法则来源于极限的四则运算法则。
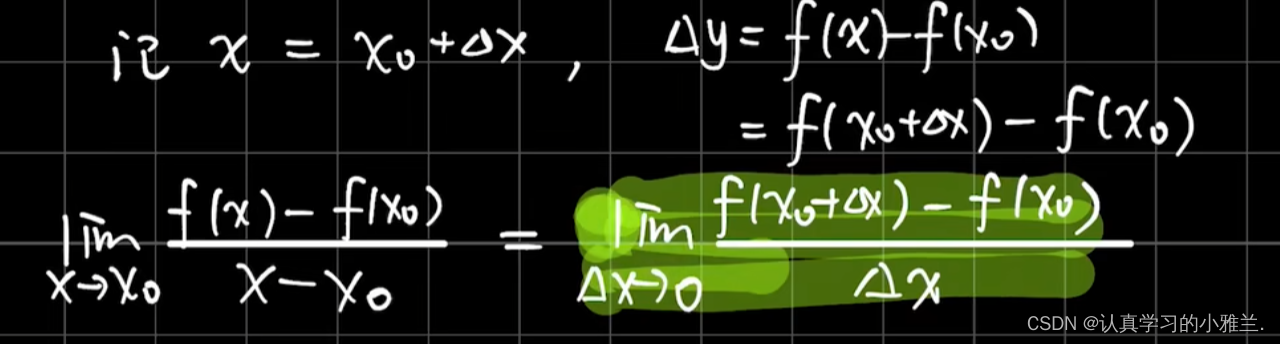
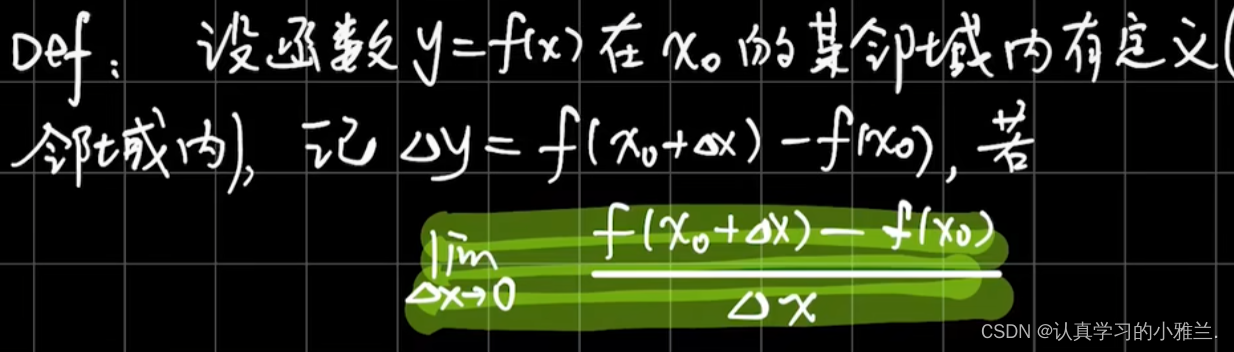
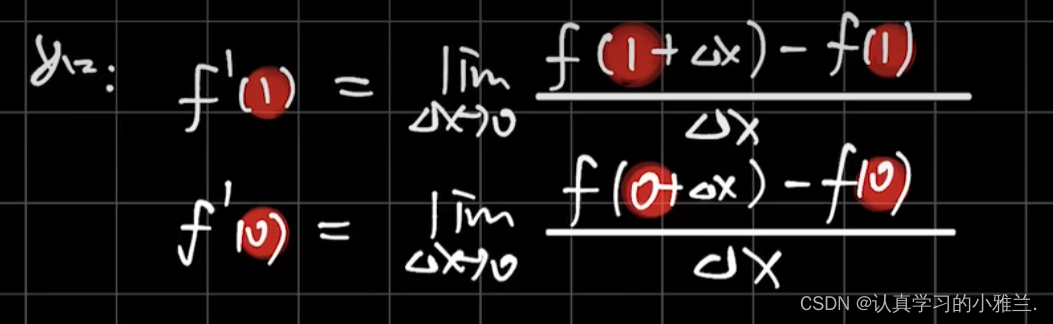
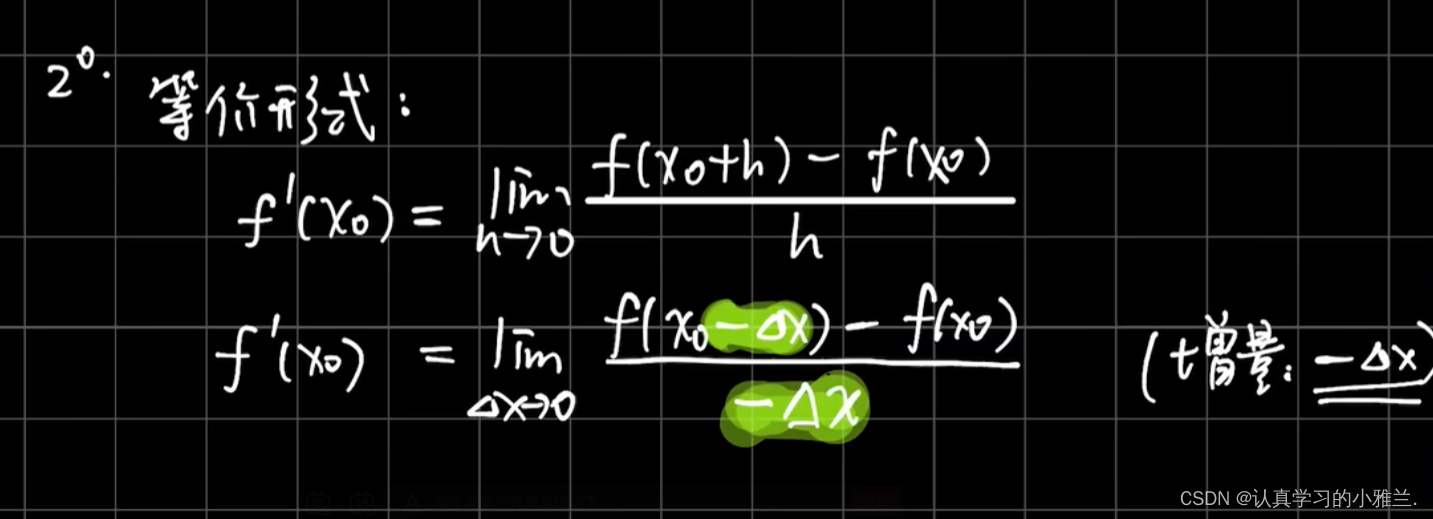
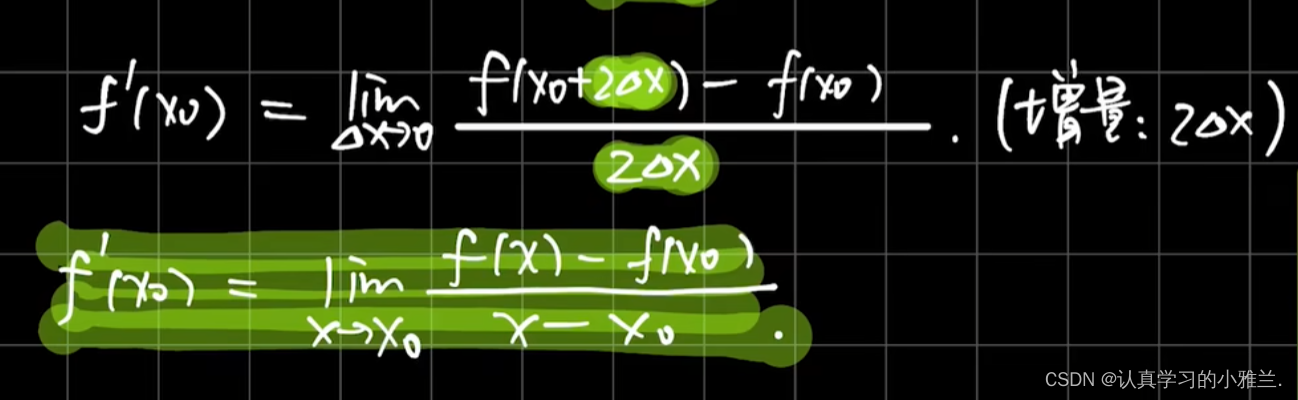
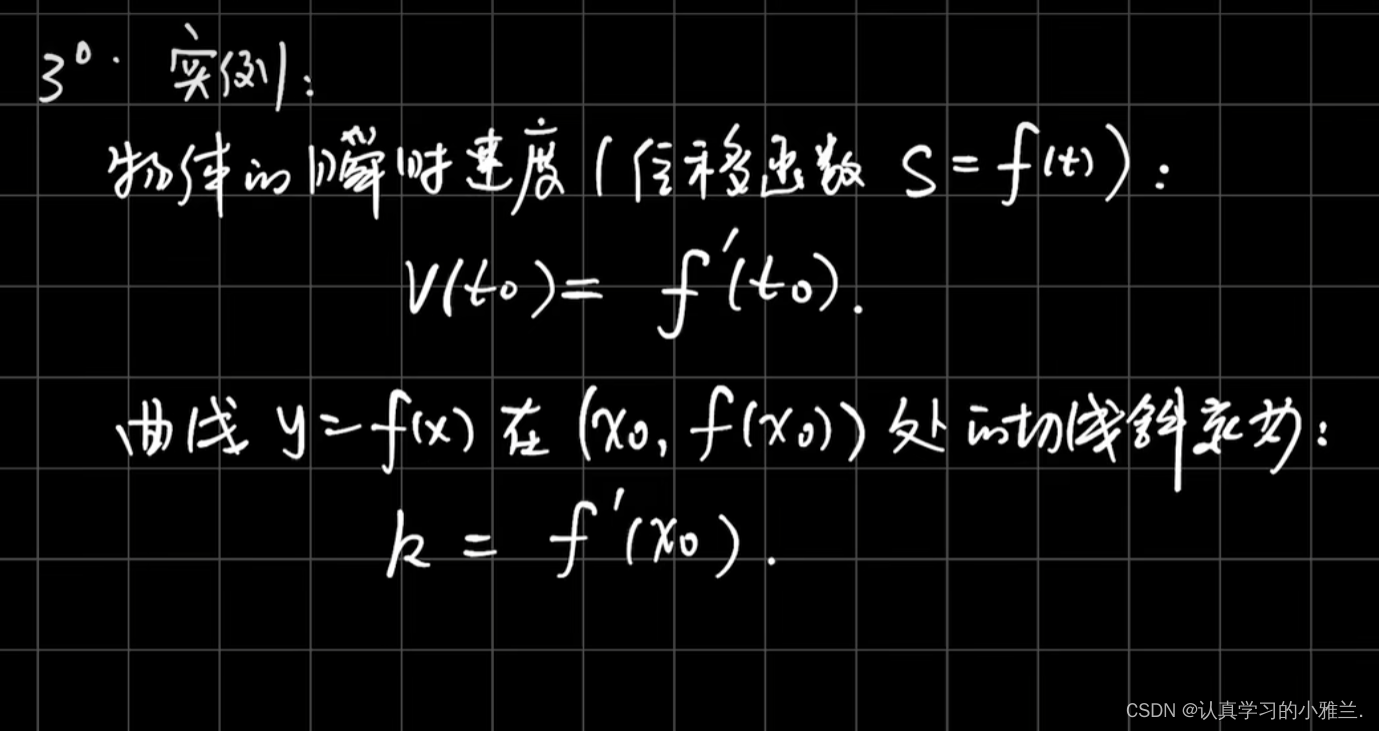
这里要注意：导数为无穷大也是导数不存在
利用导数定义求极限的例子
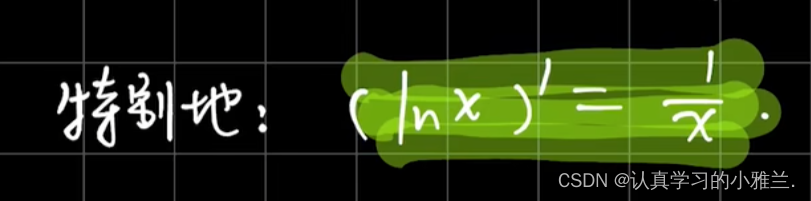
我们下面来看几个例题，其实，这些例子的结论我们高中就学过，只是当时没有证明，而是直接记的结论
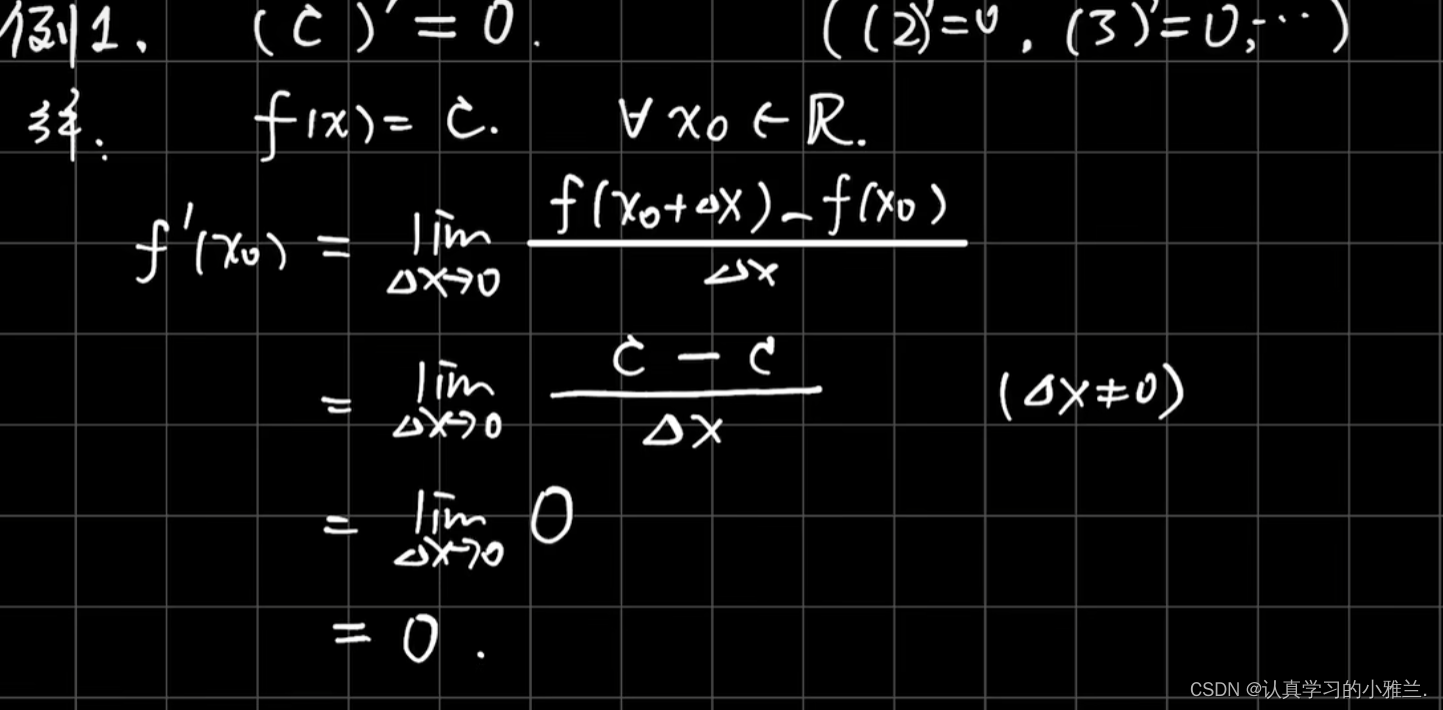
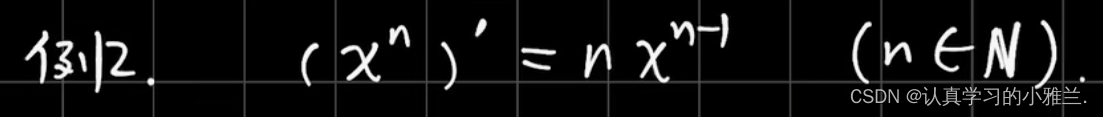
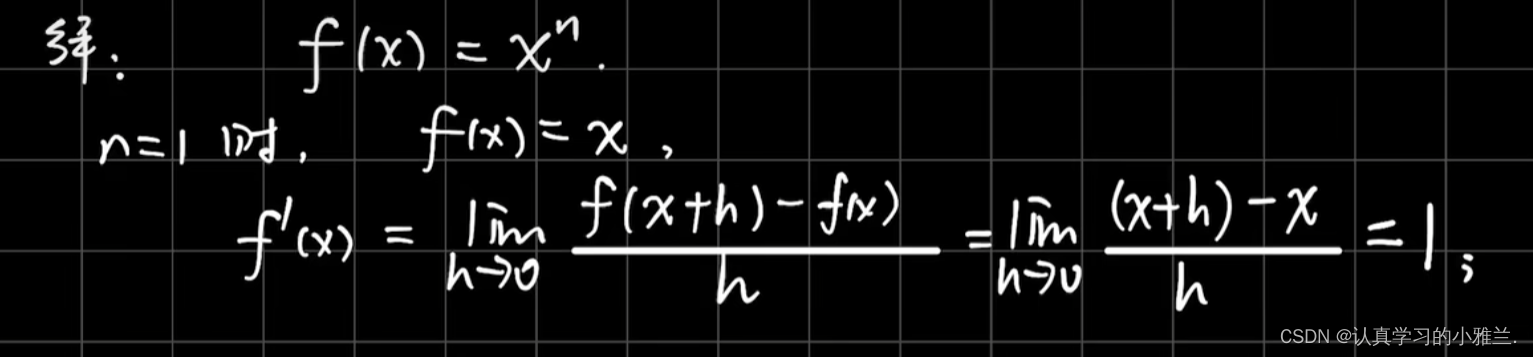
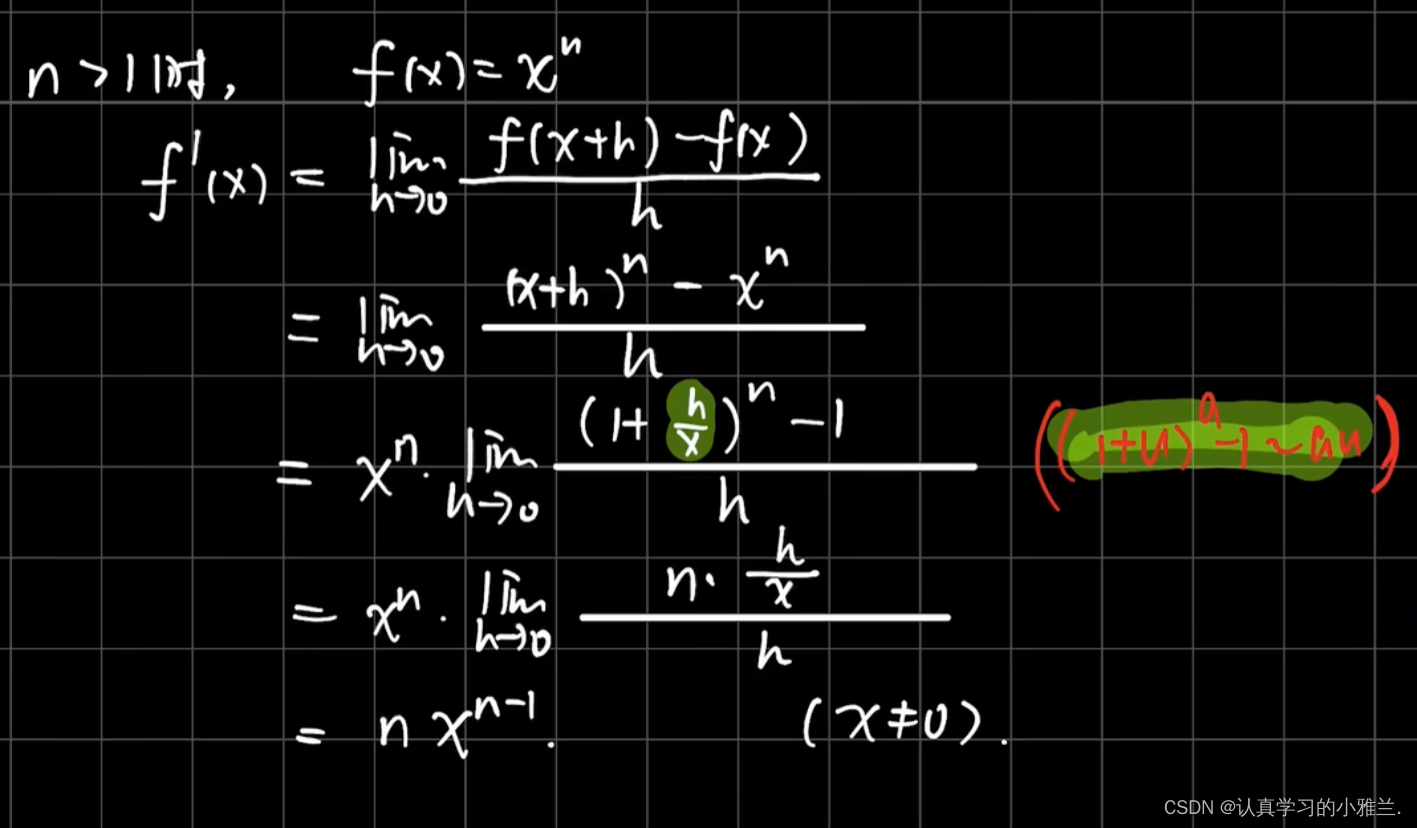
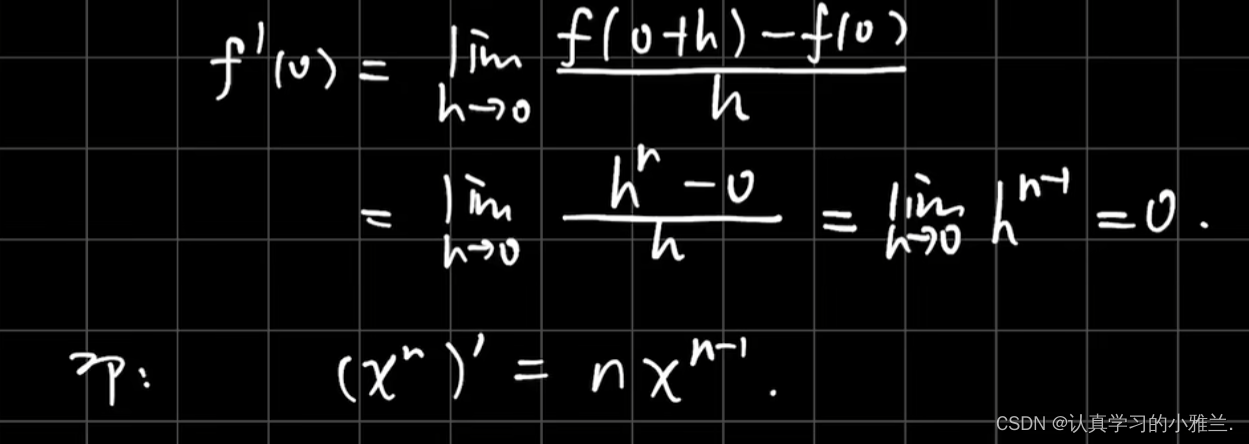
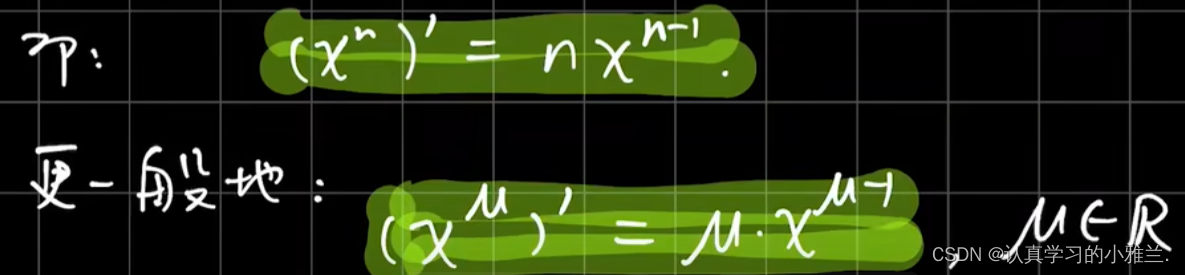
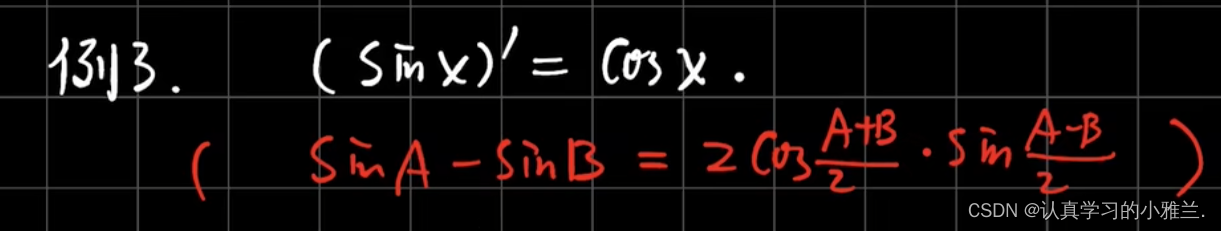
三角函数的和差化积公式
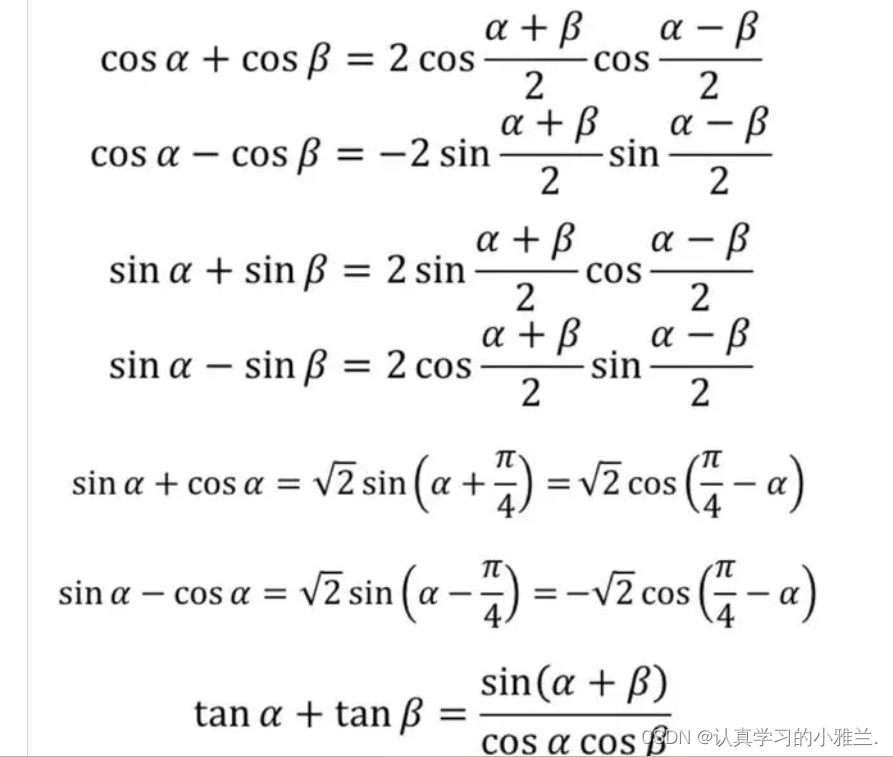
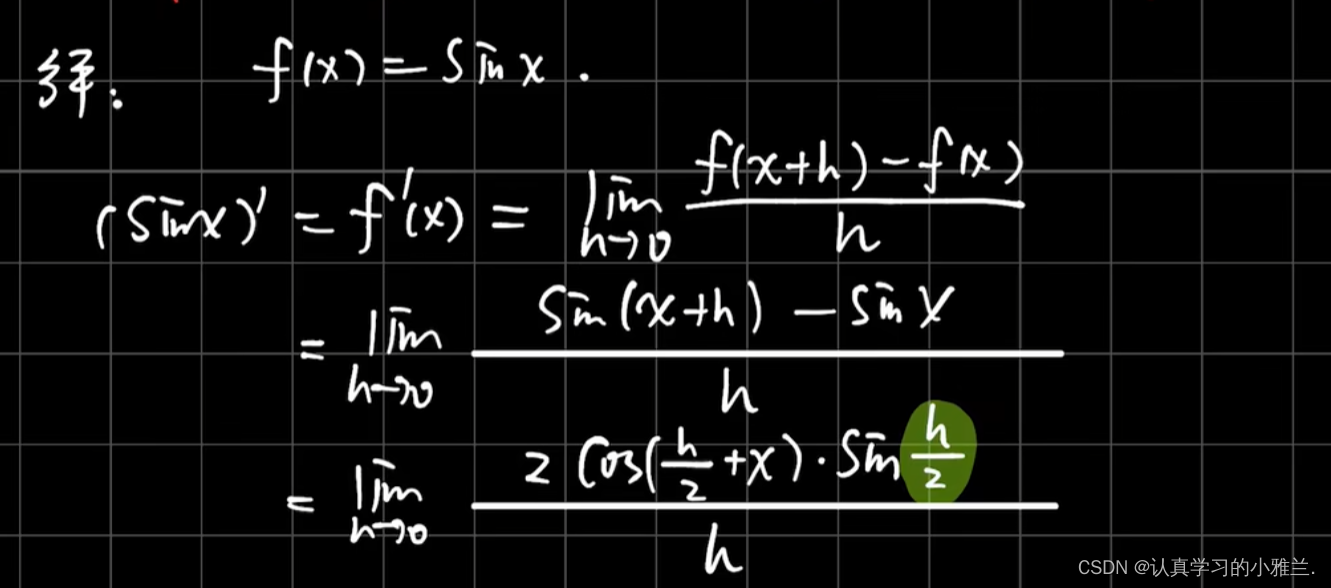
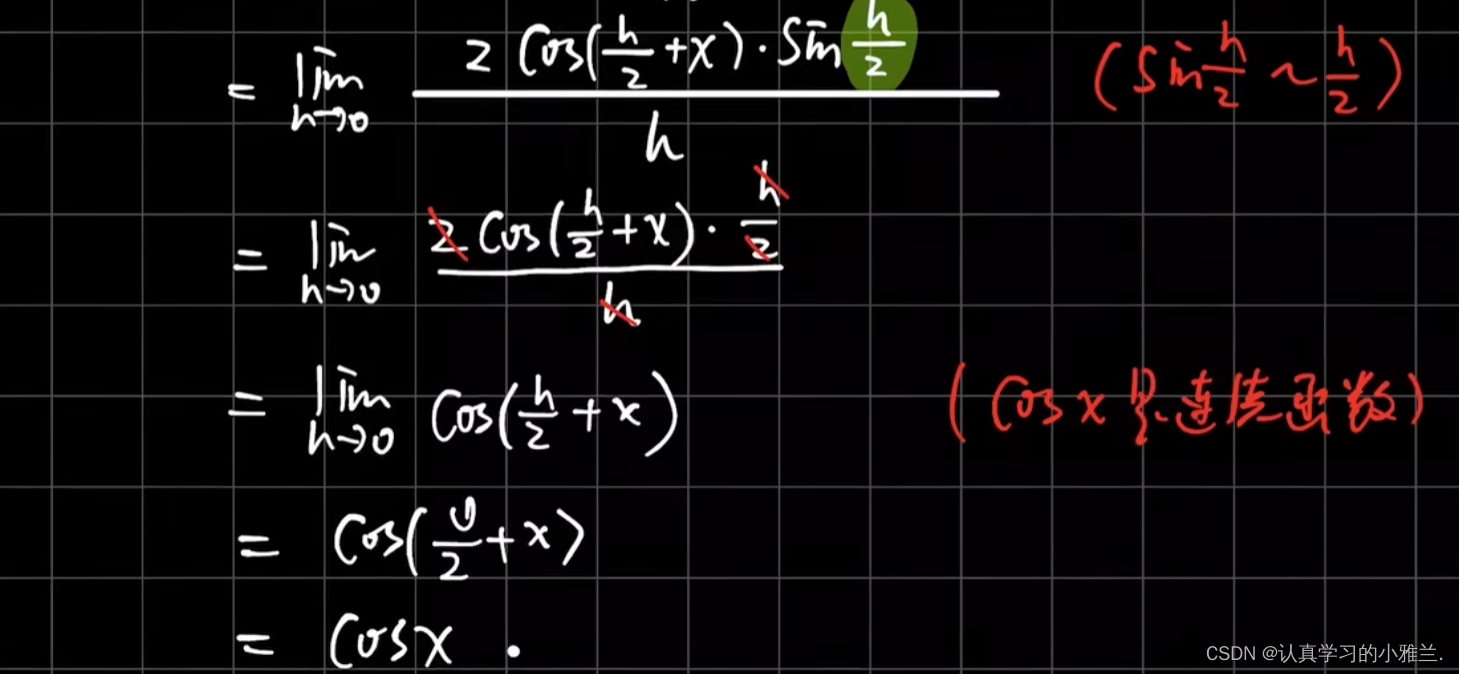
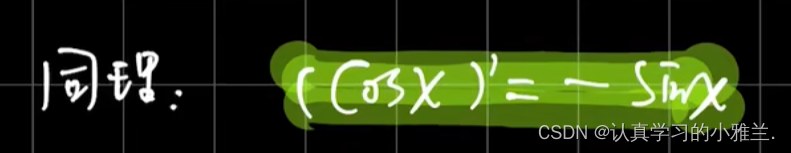
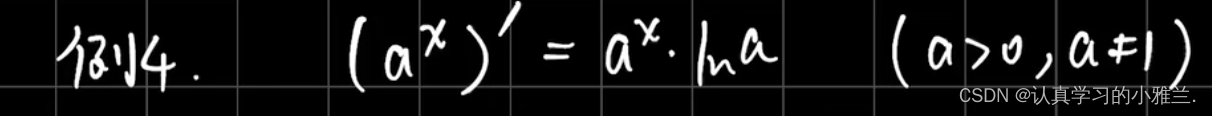
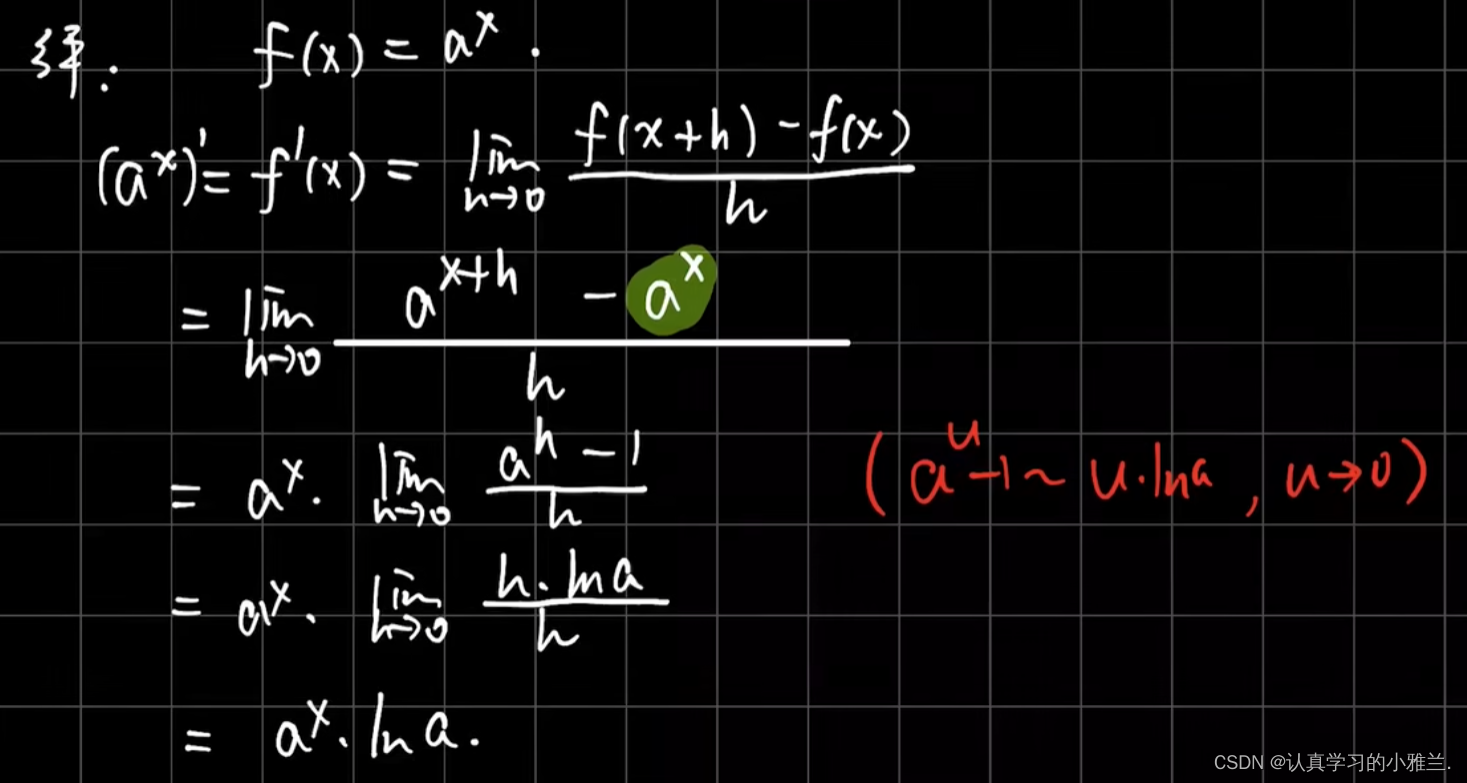
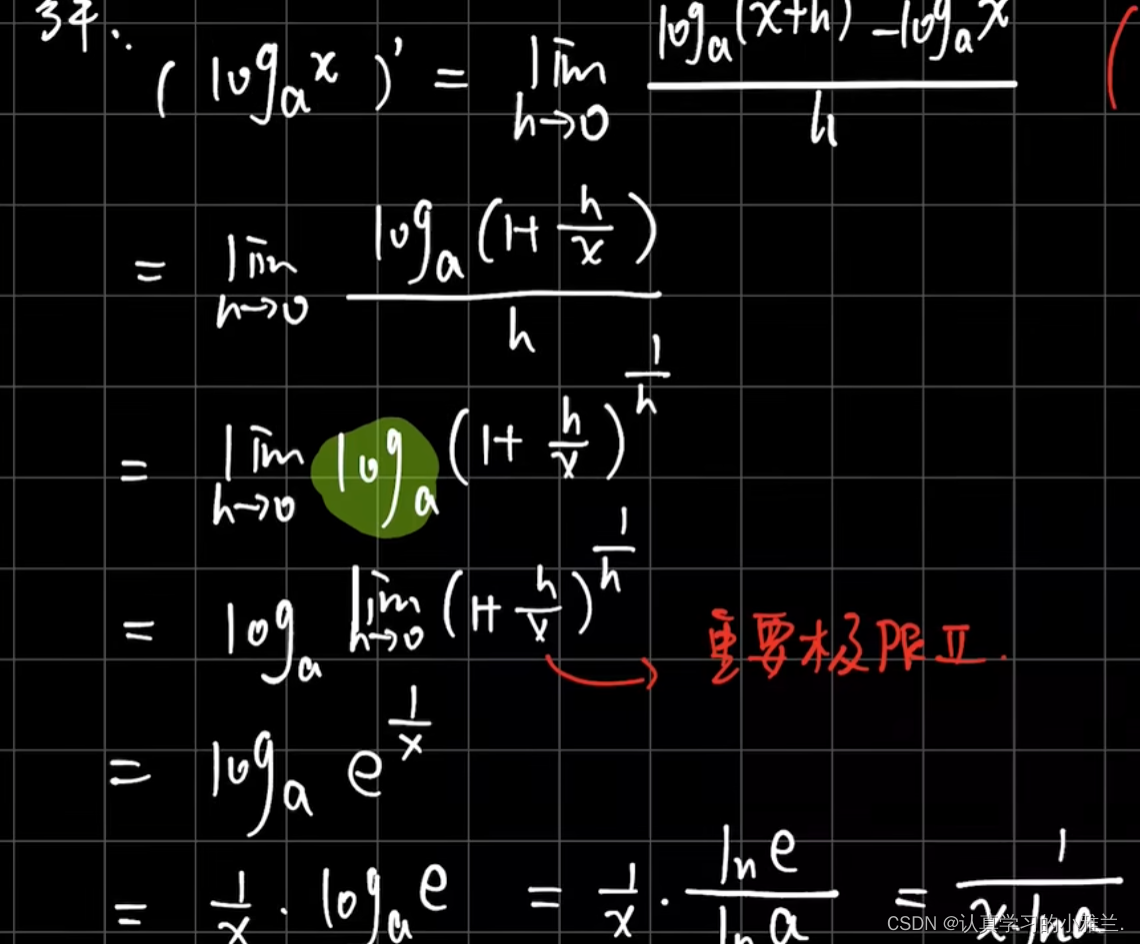
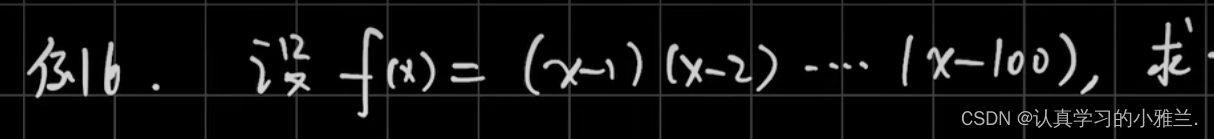
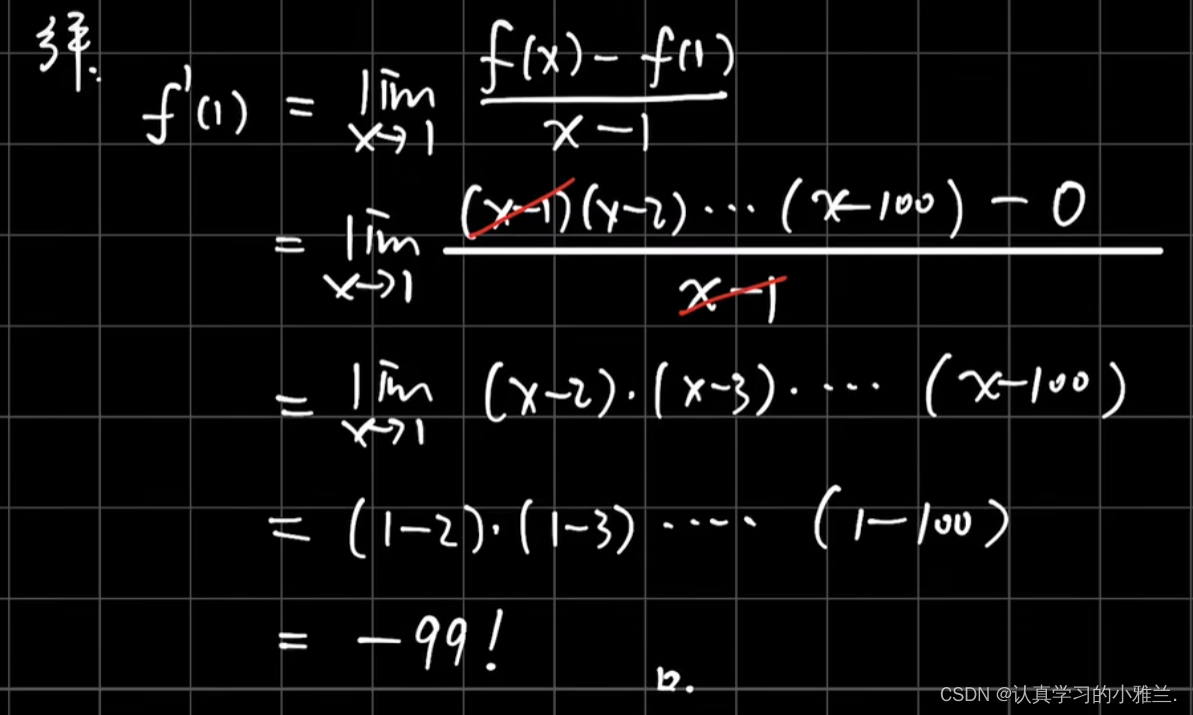
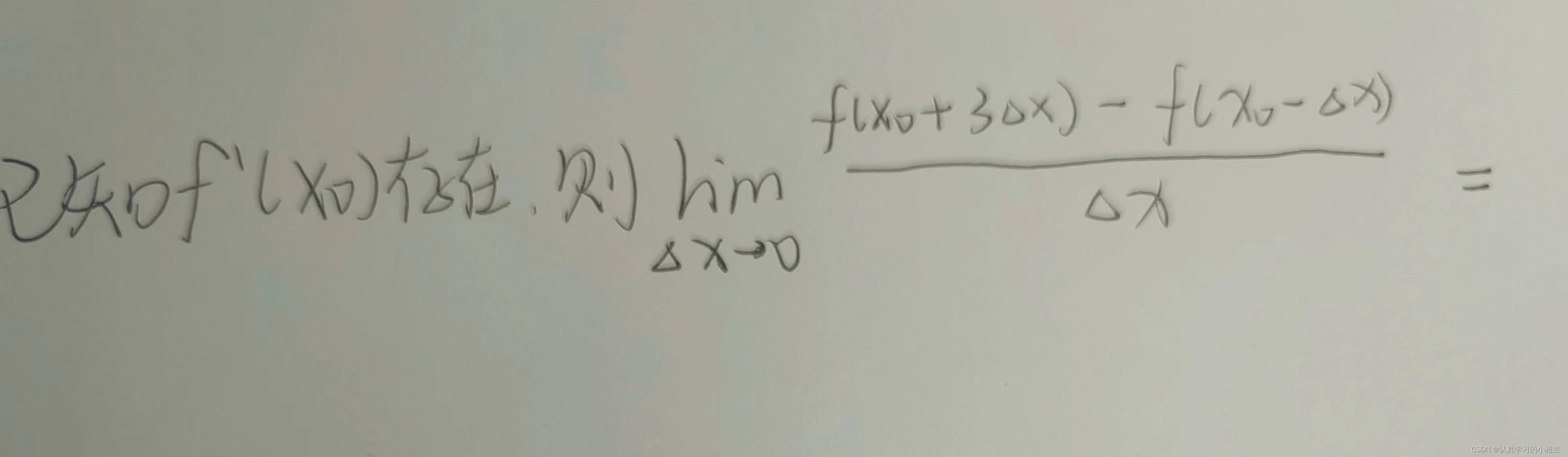
这个题目要用两次导数定义
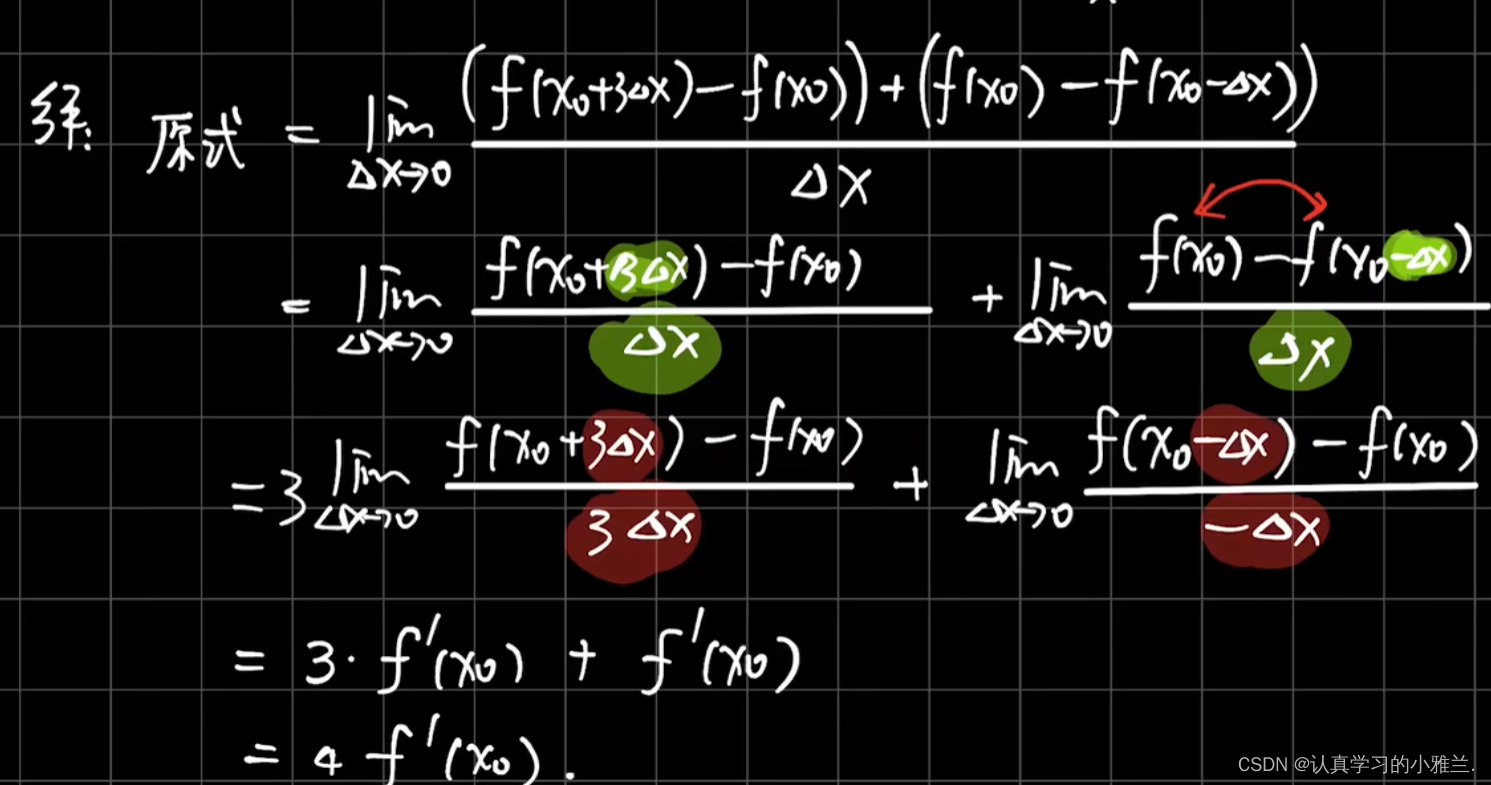
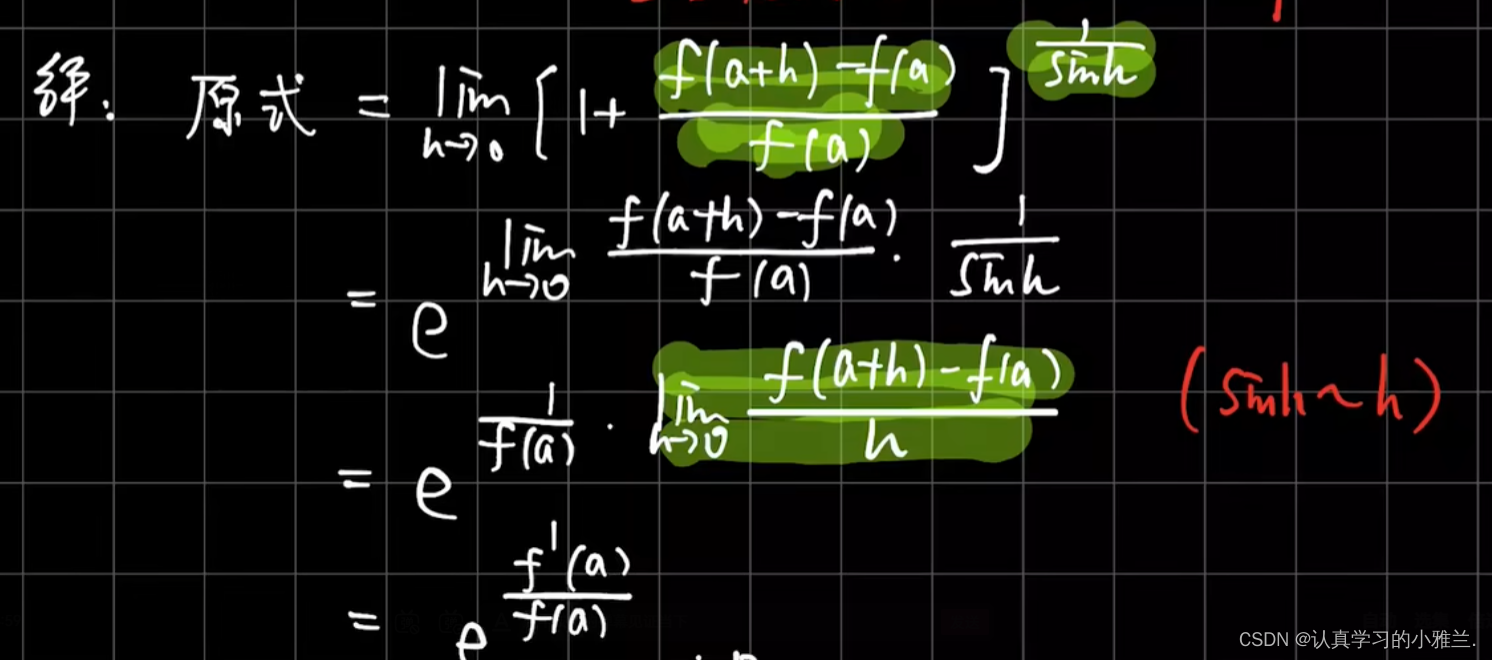
单侧导数
结论：f(x)在x0处可导的充分必要条件是f(x)在x0处左、右导数都存在且相等
下面我们来看一个具体的例子
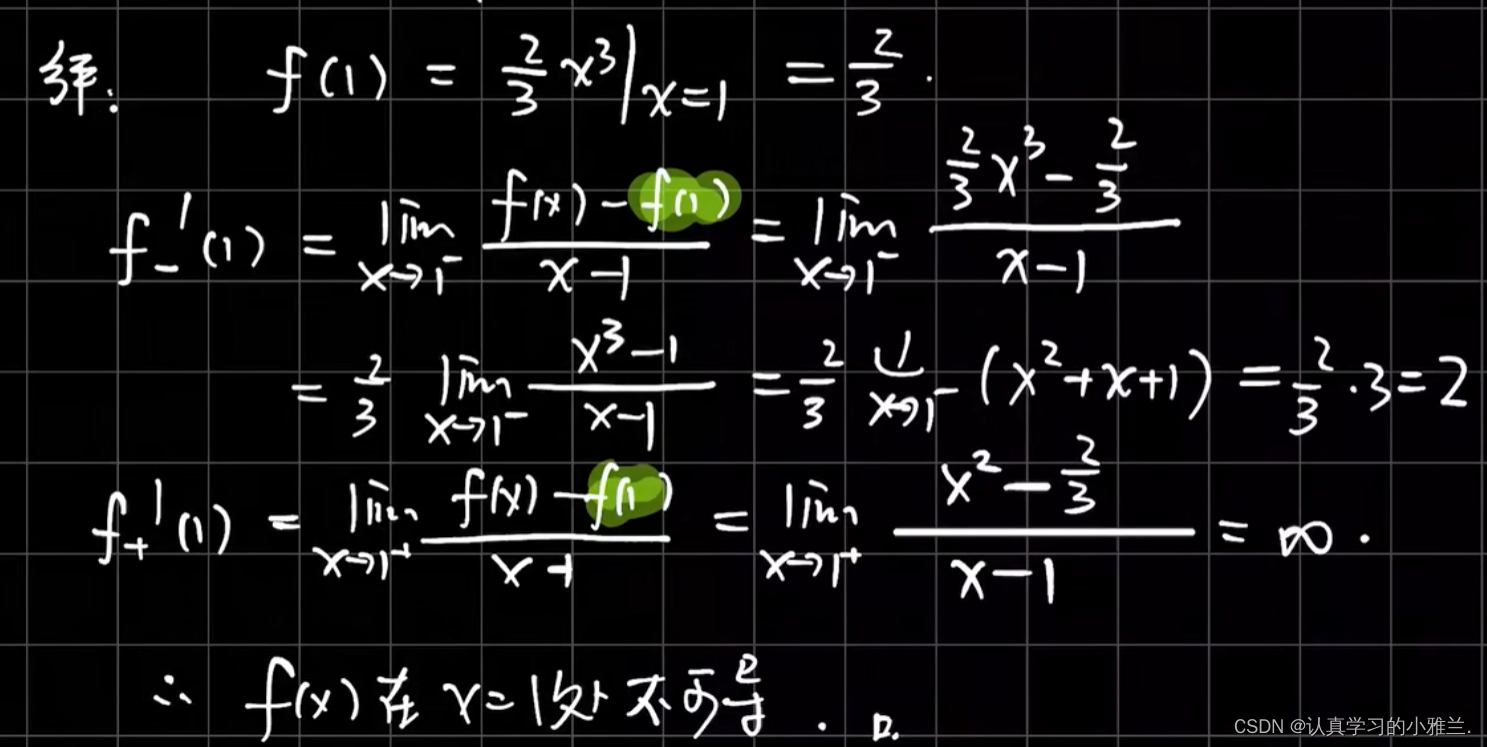
三、导数的几何意义
下面，我们来看一个例题
平行的意思是斜率相等，那么我们要求的切线方程的斜率为-2
四、可导与连续的关系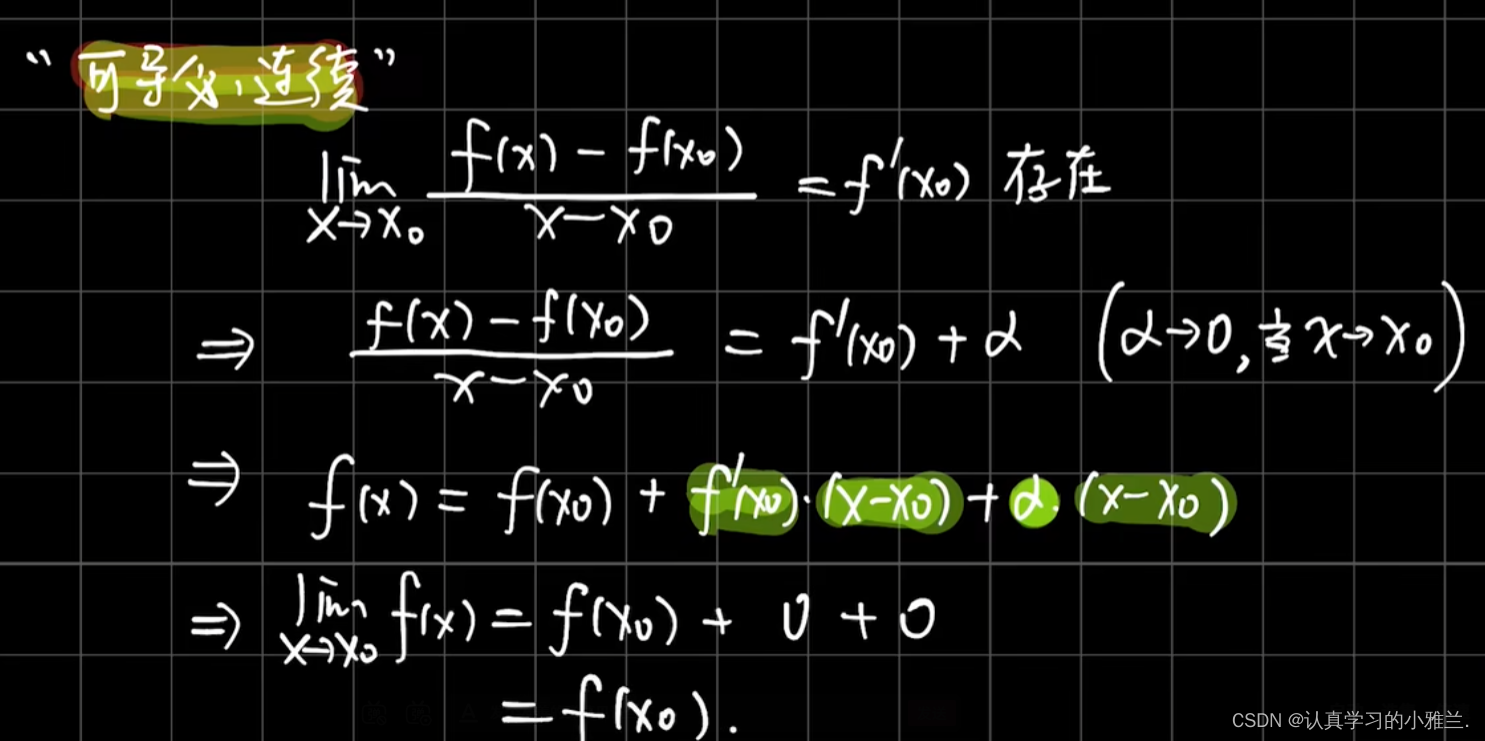 
下面，我们来看一个例题
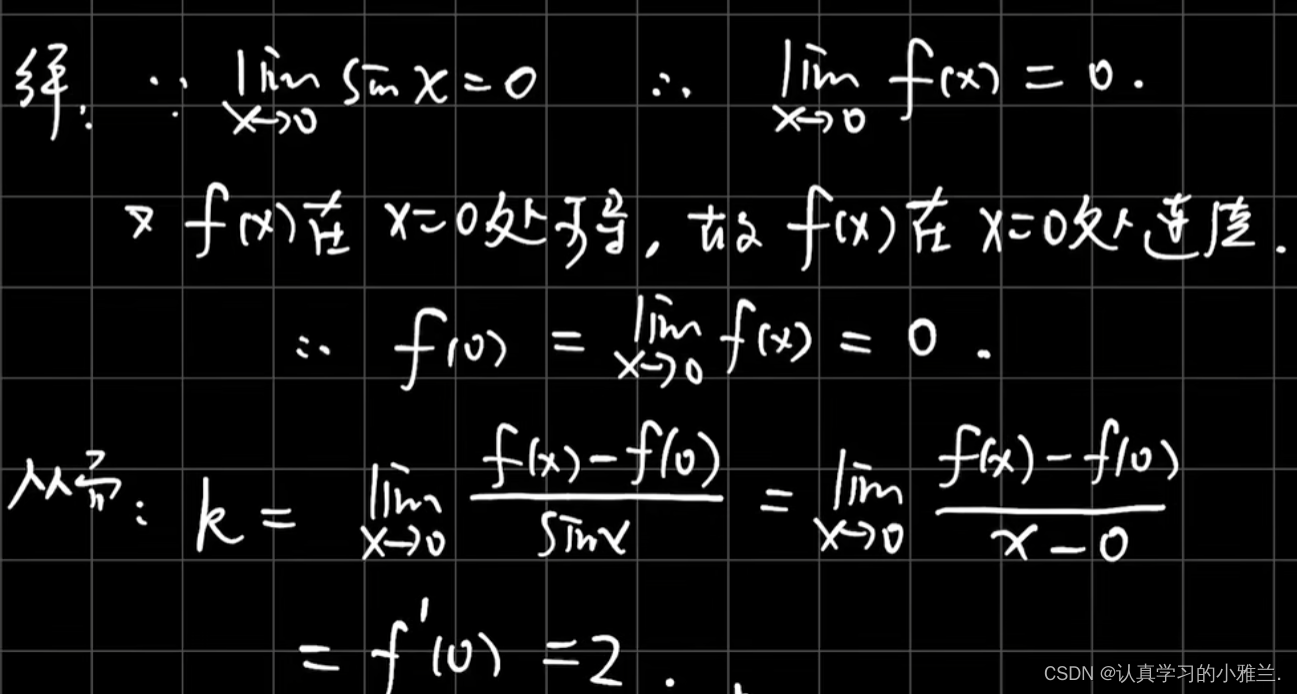
好啦，小雅兰今天的内容就到这里了，从这篇博客，我们了解到了导数的定义、导数的几何意义及可导与连续的关系，虽然内容不多，但是也有一定的难度，而且对于导数这块，小雅兰要学习的内容还有很多，哈哈，洗洗睡觉，明天继续探究导数。
