【算法】粒子群算法Particle Swarm Optimization超详细解析+代码实例讲解_粒子群算法案例

01 算法起源

粒子群优化算法(PSO)是一种进化计算技术(evolutionary computation)，1995 年由Eberhart 博士和kennedy 博士提出，源于对鸟群捕食的行为研究 。该算法最初是受到飞鸟集群活动的规律性启发，进而利用群体智能建立的一个简化模型。粒子群算法在对动物集群活动行为观察基础上，利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得最优解。

02 什么是粒子群算法？

2.1 官方定义（参照百科）

粒子群算法，也称粒子群优化算法或鸟群觅食算法（Particle Swarm Optimization），缩写为 PSO， 是近年来由J. Kennedy和R. C. Eberhart等开发的一种新的进化算法(Evolutionary Algorithm - EA)。PSO 算法属于进化算法的一种，和模拟退火算法相似，它也是从随机解出发，通过迭代寻找最优解，它也是通过适应度来评价解的品质，但它比遗传算法规则更为简单，它没有遗传算法的“交叉”(Crossover) 和“变异”(Mutation) 操作，它通过追随当前搜索到的最优值来寻找全局最优。这种算法以其实现容易、精度高、收敛快等优点引起了学术界的重视，并且在解决实际问题中展示了其优越性。粒子群算法是一种并行算法。

2.2 通俗点描述

如同前面的描述，PSO模拟的是鸟群的捕食行为。设想这样一个场景：一群鸟在随机搜索食物。在这个区域里只有一块食物。所有的鸟都不知道食物在那里。但是他们知道当前的位置离食物还有多远。那么找到食物的最优策略是什么呢。最简单有效的就是搜寻目前离食物最近的鸟的周围区域。

鸟群在整个搜寻的过程中，通过相互传递各自的信息，让其他的鸟知道自己的位置，通过这样的协作，来判断自己找到的是不是最优解，同时也将最优解的信息传递给整个鸟群，最终，整个鸟群都能聚集在食物源周围，即找到了最优解。

PSO中，每个优化问题的解都是搜索空间中的一只鸟。我们称之为“粒子”。所有的粒子都有一个由被优化的函数决定的适应值(fitness value)，每个粒子还有一个速度决定他们飞翔的方向和距离。然后粒子们就追随当前的最优粒子在解空间中搜索。

PSO 初始化为一群随机粒子(随机解)。然后通过迭代找到最优解。在每一次迭代中，粒子通过跟踪两个"极值"来更新自己。第一个就是粒子本身所找到的最优解，这个解叫做个体极值pBest。另一个极值是整个种群目前找到的最优解，这个极值是全局极值gBest。另外也可以不用整个种群而只是用其中一部分作为粒子的邻居，那么在所有邻居中的极值就是局部极值。

2.3 再再再通俗点的描述

粒子群算法的基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。如上的情景。试着想一下一群鸟在寻找食物，在这个区域中只有一只虫子，所有的鸟都不知道食物在哪。但是它们知道自己的当前位置距离食物有多远，同时它们知道离食物最近的鸟的位置。想一下这时候会发生什么？

同时各只鸟在位置不停变化时候离食物的距离也不断变化，所以每个鸟一定有过离食物最近的位置，这也是它们的一个参考。

所以，粒子群算法就是把鸟看成一个个粒子，并且他们拥有位置和速度这两个属性，然后根据自身已经找到的离食物最近的解和参考整个共享于整个集群中找到的最近的解去改变自己的飞行方向，最后我们会发现，整个集群大致向同一个地方聚集。而这个地方是离食物最近的区域，条件好的话就会找到食物。

03 粒子抽象

3.1 关于速度和位置

粒子群算法通过设计一种无质量的粒子来模拟鸟群中的鸟，粒子仅具有两个属性：速度和位置，速度代表移动的快慢，位置代表移动的方向。

鸟被抽象为没有质量和体积的微粒(点)，并延伸到N维空间，粒子i在N维空间的位置表示为矢量Xi＝(x1，x2，…，xN)，飞行速度表示为矢量Vi＝(v1，v2，…，vN)。每个粒子都有一个由目标函数决定的适应值(fitness value)，并且知道自己到目前为止发现的最好位置(pbest)和现在的位置Xi。这个可以看作是粒子自己的飞行经验。除此之外，每个粒子还知道到目前为止整个群体中所有粒子发现的最好位置(gbest)(gbest是pbest中的最好值)，这个可以看作是粒子同伴的经验。粒子就是通过自己的经验和同伴中最好的经验来决定下一步的运动。

3.2 速度和位置的更新

PSO初始化为一群随机粒子(随机解)。然后通过迭代找到最优解。在每一次的迭代中，粒子通过跟踪两个“极值”(pbest，gbest)来更新自己。在找到这两个最优值后，粒子通过下面的公式来更新自己的速度和位置。

对于公式(1)：

公式(1)的第①部分称为【记忆项】，表示上次速度大小和方向的影响；

公式(1)的第②部分称为【自身认知项】，是从当前点指向粒子自身最好点的一个矢量，表示粒子的动作来源于自己经验的部分；

公式(1)的第③部分称为【群体认知项】，是一个从当前点指向种群最好点的矢量，反映了粒子间的协同合作和知识共享。粒子就是通过自己的经验和同伴中最好的经验来决定下一步的运动。

以上面两个公式为基础，再来看一个公式：

公式(2)和 公式(3)被视为标准PSO算法。

04 标准PSO算法流程

4.1 标准PSO算法的流程

1）初始化一群微粒(群体规模为N)，包括随机位置和速度；

2）评价每个微粒的适应度；

3）对每个微粒，将其适应值与其经过的最好位置pbest作比较，如果较好，则将其作为当前的最好位置pbest；

4）对每个微粒，将其适应值与其经过的最好位置gbest作比较，如果较好，则将其作为当前的最好位置gbest；

5）根据公式(2)、(3)调整微粒速度和位置；

6）未达到结束条件则转第2）步。

迭代终止条件根据具体问题一般选为最大迭代次数Gk或(和)微粒群迄今为止搜索到的最优位置满足预定最小适应阈值。

4.2 PSO流程图解

4.3 学习因子c1、c2分析

公式(2)和(3)中pbest和gbest分别表示微粒群的局部和全局最优位置。

当C1＝0时，则粒子没有了认知能力，变为只有社会的模型(social-only)：

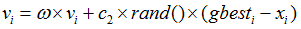
称为全局PSO算法。粒子有扩展搜索空间的能力，具有较快的收敛速度，但由于缺少局部搜索，对于复杂问题
比标准PSO 更易陷入局部最优。
当C2＝0时，则粒子之间没有社会信息，模型变为只有认知(cognition-only)模型：

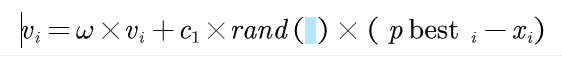
称为局部PSO算法。由于个体之间没有信息的交流，整个群体相当于多个粒子进行盲目的随机搜索，收敛速度慢，因而得到最优解的可能性小。

05 代码实例讲解

5.1 先来看个简单的实例

粒子群优化算法求解函数y=x+x*sin(x)在[-10, 10]的最大值.

pso.m
下面先看代码和代码注释。

function [best_x, best_y]=pso()
%find the max value of a function
%Author: kailugaji https://www.cnblogs.com/kailugaji/
posMax=10;posMin=-10;  %range of feasible solution
x=posMin:0.1:posMax;
y=my_fun(x);  %object function
plot(x,y);hold on; %plot function
popsize=30;  %number of particles
max_iter=100;  %maximum number of iterations
position=rand(popsize,1);
position=position*20-ones(popsize,1)*10;   %particle's position
vMax=1;vMin=-1;  %range of velocity
velosity=2*rand(popsize,1)-1;  %path direction
pbest=position;  %current optimum
gbest=position(1);  %global optimum
wBegin=1;wEnd=0.05;
c1=2;  %weight of local information
c2=2;  %weight of global information
for i=1:max_iter
    position_new=position+velosity;  %change direction of each particle
    velosity_new=(wEnd+(wBegin-wEnd)*(100-i)/100).*velosity+c1*rand().*(position-pbest.*ones(popsize,1))+c2*rand().*(position-gbest.*ones(popsize,1));  %inertia+personal influence+social influence
    for j=1:popsize
        if(position_new(j)>posMax)
            position_new(j)=posMax;
        end
        if(position_new(j)<posMin)
            position_new(j)=posMin;
        end
        if(velosity_new(j)>vMax)
            velosity_new(j)=vMax;
        end
        if(velosity_new(j)<vMin)
            velosity_new(j)=vMin;
        end
         if(my_fun(position_new(j))>my_fun(pbest(j)))
            pbest(j)=position_new(j);
        end
        if(my_fun(position_new(j))>my_fun(gbest))
            gbest=position_new(j);
        end
    end
    position=position_new;
    velosity=velosity_new;
end
plot(gbest,my_fun(gbest),'or');
best_x=gbest;
best_y=my_fun(gbest);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

my_fun.m

function y=my_fun(x)
y=x+x.*sin(x);
1
2

[best_x, best_y]=pso()
best_x =
8.0051
best_y =
15.9190

5.2 实例2

在这个例子中，我们选取了一个求解函数y=-x*(x-1) 在0,2上最大值的粒子群算法。然后通过步步跟踪算法输出结果，来给大家讲解粒子运动的过程。

下面先看代码和代码注释。

public class AlgorithmPSO {
	int n=2; //粒子个数，这里为了方便演示，我们只取两个，观察其运动方向
    double[] y;
    double[] x;
    double[] v;
    double c1=2;
    double c2=2;
    double pbest[];
    double gbest;
    double vmax=0.1; //速度最大值
    //适应度计算函数，每个粒子都有它的适应度
    public void fitnessFunction(){
        for(int i=0;i<n;i++){
            y[i]=-1*x[i]*(x[i]-2);
        }
    }
    public void init(){ //初始化
        x=new double[n];
        v=new double[n];
        y=new double[n];
        pbest=new double[n];
        /***
         * 本来是应该随机产生的，为了方便演示，我这里手动随机落两个点，分别落在最大值两边
         */
        x[0]=0.0;
        x[1]=2.0;
        v[0]=0.01;
        v[1]=0.02;
        fitnessFunction();
        //初始化当前个体最优位置，并找到群体最优位置
        for(int i=0;i<n;i++){
            pbest[i]=y[i];
            if(y[i]>gbest) gbest=y[i];
        }
        System.out.println("算法开始，起始最优解:"+gbest);
        System.out.print("\n");
    }
    public double getMAX(double a,double b){
        return a>b?a:b;
    }
    //粒子群算法
    public void PSO(int max){
        for(int i=0;i<max;i++){
            double w=0.4;
            for(int j=0;j<n;j++){
                //更新位置和速度，下面就是我们之前重点讲解的两条公式。
                v[j]=w*v[j]+c1*Math.random()*(pbest[j]-x[j])+c2*Math.random()*(gbest-x[j]);
                if(v[j]>vmax) v[j]=vmax;//控制速度不超过最大值
                x[j]+=v[j];
                
                //越界判断，范围限定在[0, 2]
                if(x[j]>2) x[j]=2;
                if(x[j]<0) x[j]=0;
                
            }
            fitnessFunction();
            //更新个体极值和群体极值
            for(int j=0;j<n;j++){
                pbest[j]=getMAX(y[j],pbest[j]);
                if(pbest[j]>gbest) gbest=pbest[j];
                System.out.println("粒子n"+j+": x = "+x[j]+"  "+"v = "+v[j]);
            }
            System.out.println("第"+(i+1)+"次迭代，全局最优解 gbest = "+gbest);
            System.out.print("\n");
        }
        
    }
    //运行我们的算法
    public static void main(String[] args){
    	AlgorithmPSO ts=new AlgorithmPSO();
        ts.init();
        ts.PSO(10);//为了方便演示，我们暂时迭代10次。
    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75

输出结果：

算法开始，起始最优解:0.0

粒子n0: x = 0.004  v = 0.004
粒子n1: x = 0.0  v = -4.065770842472382
第1次迭代，全局最优解 gbest = 0.007984

粒子n0: x = 0.01778510589090629  v = 0.013785105890906289
粒子n1: x = 0.0  v = -1.625639647649872
第2次迭代，全局最优解 gbest = 0.03525390179026183

粒子n0: x = 0.0610276658084214  v = 0.04324255991751511
粒子n1: x = 0.0  v = -0.6035255880722042
第3次迭代，全局最优解 gbest = 0.11833095562281844

粒子n0: x = 0.1610276658084214  v = 0.1
粒子n1: x = 0.0  v = -0.012719944703824898
第4次迭代，全局最优解 gbest = 0.29612542246113416

粒子n0: x = 0.2610276658084214  v = 0.1
粒子n1: x = 0.06231495466940402  v = 0.06231495466940402
第5次迭代，全局最优解 gbest = 0.4539198892994499

粒子n0: x = 0.3610276658084214  v = 0.1
粒子n1: x = 0.16231495466940402  v = 0.1
第6次迭代，全局最优解 gbest = 0.5917143561377656

粒子n0: x = 0.46102766580842136  v = 0.1
粒子n1: x = 0.262314954669404  v = 0.1
第7次迭代，全局最优解 gbest = 0.7095088229760813

粒子n0: x = 0.5610276658084213  v = 0.1
粒子n1: x = 0.362314954669404  v = 0.1
第8次迭代，全局最优解 gbest = 0.8073032898143969

粒子n0: x = 0.6610276658084213  v = 0.1
粒子n1: x = 0.462314954669404  v = 0.1
第9次迭代，全局最优解 gbest = 0.8850977566527127

粒子n0: x = 0.7610276658084213  v = 0.1
粒子n1: x = 0.562314954669404  v = 0.1
第10次迭代，全局最优解 gbest = 0.9428922234910285

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

现在我们来观察两个粒子的位移x在每一次迭代中的变化（离食物的距离）。

1. 初始状态

粒子n0: x = 0.0 v = 0.01

粒子n1: x = 2.0 v = 0.02

两个粒子位于区间两端。

2. 第一次迭代

粒子n0: x = 0.004 v = 0.004

粒子n1: x = 0.0 v = -4.065770842472382

两个粒子都跑到原点了。

3. 第二、三……十次迭代
   

可以看到，两个粒子在不断靠近最优点。上面多个圈是他们聚集的过程，可以看出来，聚集过程是个越来越密集的过程。这才是10次迭代而已。如果我们加大迭代次数，很容易就找出最优解了。最后放上一个迭代100次的结果：

相信通过这个简单的例子。大家已经对粒子群算法有了非常清晰的认识了。

06 PSO和GA比较

6.1 共性

(1)都属于仿生算法。

(2) 都属于全局优化方法。

(3) 都属于随机搜索算法。

(4) 都隐含并行性。

(5) 根据个体的适配信息进行搜索，因此不受函数 约束条件的限制，如连续性、可导性等。

(6) 对高维复杂问题，往往会遇到早熟收敛和收敛 性能差的缺点，都无法保证收敛到最优点。

6.2 差异

(1) PSO有记忆，好的解的知识所有粒子都保 存，而GA，以前的知识随着种群的改变被改变。

(2) PSO中的粒子仅仅通过当前搜索到最优点进行共享信息，所以很大程度上这是一种单共享项信息机制。而GA中，染色体之间相互共享信息，使得整个种群都向最优区域移动。

(3) GA的编码技术和遗传操作比较简单，而PSO 相对于GA，没有交叉和变异操作，粒子只是通过内部速度进行更新，因此原理更简单、参数更少、实现更容易。