C++算法 —— 位运算_c++位运算

一、基本的位运算操作

1.基础位运算操作符

<< : 二进制位整体左移

>> : 二进制位整体右移

~ : 按位取反

& ： 按位与

| ： 按位或

^ : 按位异或 （无进位相加）

2.给一个数n，确定它的二进制表示中第x位置表示的是1还是0

(n >> x) & 1

3.将一个数n的二进制位第x位改成1

(1<<x) & n 

4.将一个数n的二进制位第x位改成0

(~(1<<x)) & n

5.位图的思想

位图就是一种利用比特位去承载信息的一种哈希思想，通常可以用来记录“在不在”等问题，利用32位比特位的一位或者多位去记录某种信息状态，和哈希表利用数组是一样的，位图是解决一些大基数的简单问题，具体操作这里不做详细整理

6.提前一个数（n）二进制位中最右边的1

n&(-n)

解释：因为-n就是将n的二进制先按位取反，然后再+1，例如：

原码：01100100
补码：10011011
反码：10011100

我们会发现将n变成-n之后，最右侧的1往后位置都保持不变，而1前面的位置的都相反，这是由于取反后又加1，前面部分不同因为取了反，后面因为加1进位，使得最右侧的1和原先的保持，所以n&(-n)可以提取最后一位1

7.干掉一个数（n）二进制位中最右边的1

n&(n-1)

这个太常见了，因为最后减1会相最右侧的1借位，所以n-1最右侧的1以后都会不同，而不影响前面

8.位运算的优先级

管它什么优先级，按自己的思路加括号！！！

9.异或运算的运算律

a^b^c = a^(b^c) ，即异或操作不在乎顺序

利用该性质有一个经典且量身定做的题目：只出现一次的数字 以及其变形  只出现一次的数字|||

因为太经典了，一搜就搜到了，简单提供下思路，只出现一次的数字，就是有一个数只有一个，其他都是成对出现的，因此只需要拿一个0去将这组数全部异或，最终结果就是那个只出现一次的数

而只出现一次的数字|||相对需要做一些处理，题目大致和原先一样，不过有两个只出现了一次的数字，其余都是出现两次的相同数，这个时候需要先将这组数据进行处理，还是利用异或去将这组数据进行分组，假如不同的那两个数是a和b，将a和b异或后，一定会有一个不等于0的数，我们拿到这个数最右侧的1位置去将数据分成两组数据，相同数据一定会被分到一组中，而那两个不同的数会被分到不同组中，此时问题就变回原先的模型了

二、判断字符是否唯一

1.链接

面试题 01.01. 判定字符是否唯一 - 力扣（LeetCode）

2.描述

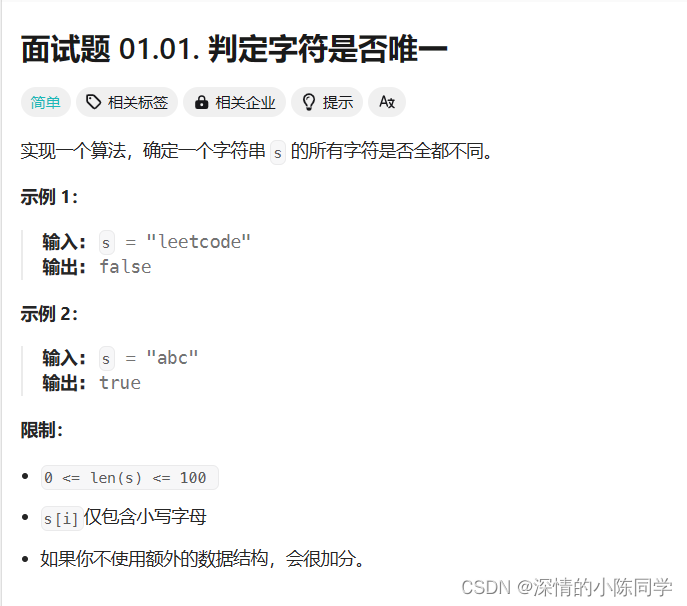
3.思路

该题目若是不考虑额外的限制条件，则只需要使用哈希表，遍历字符串的同时若是遇到已经存在的字符则返回false，若是没有则存入字符到哈希表中，最终遍历结束后都没有重复则返回true

优化：题目要求若是不用额外的数据结构在面试中会很加分，我们可以使用位图的思想去完成，因为题目中提到只有小写字母，因此只有26种字符，所以直接用一个整形中的32bit位即可完成，思路上和哈希统计是没有区别的，只不过在使用位图的时候，更多的是通过位运算的操作，例如如果将某位变成1等等

4.参考代码

class Solution {
public:
    bool isUnique(string astr) 
    {
        if(astr.size() > 26) return false;
        int hash = 0;
        for(int i = 0;i<astr.size();i++)
        {
            int x = astr[i] - 'a';
            if( ( ( hash>>x )&1 ) == 0 ) 
                hash |= 1<<x;
            else
                return false;
        }
        return true;
    }
};

三、丢失的数字

1.链接

268. 丢失的数字 - 力扣（LeetCode）

2.描述

3.思路

这题的方法很多：哈希、二分法、数学方法、位运算

可以使用哈希表的方式去统计

也可以采用二分法，这和之前做过的一题点名很像

数学方法则是高斯求和，先将0到n的和算出来，然后减去数组和即可

位运算则是用异或的性质，将数组中所有数进行异或，然后再和0到n的数异或

4.参考代码

这里只提供一个位运算的代码参考，其他的都挺简单，可以自己尝试去写写

class Solution {
public:
    int missingNumber(vector<int>& nums) 
    {
        int n = 0;
        for(auto& x:nums) n^=x;
        for(int i = 0;i<=nums.size();i++) n^=i;
        return n;
    }
};

四、两数之和

1.链接

371. 两整数之和 - 力扣（LeetCode）

2.描述

3.思路

两数之和我们利用位运算中的按位异或，按位异或可以被看作为无进位相加，也就是说，只要处理好进位的问题，就可以实现相加，而进位可以通过按位与去得到那些部分需要进位

4.参考代码

class Solution 
{
public:
    int getSum(int a, int b) 
    {
        int ret = a^b;
        unsigned int up = a&b;
        while(up)
        {
            int tmp = ret^(up<<1);
            up = ret&(up<<1);
            ret = tmp;
        }
        return ret;
    }
};

五、只出现一次的数||

1.链接

137. 只出现一次的数字 II - 力扣（LeetCode）

2.描述

3.思路

4.参考代码

class Solution {
public:
    int singleNumber(vector<int>& nums) 
    {
        int ret = 0;
        for(int i = 0;i<32;i++)
        {
            int bit = 0;
            for(auto x : nums)
            {
                bit +=((x>>i)&1);
            }
            bit%=3;
            if(bit == 1) ret |= (1<<i);
        }
        return ret;
    }
};

六、消失的两个数字

1.链接

面试题 17.19. 消失的两个数字 - 力扣（LeetCode）

2.描述

3.思路

这题的思路我们可以认为，是《消失的数字》+《只出现一次的数字|||》两个题目的合并，我们只需用一个0将【1，N】的数字都异或一次，再将数组里的数异或一次，就可以得到那消失的两个数的异或，再通过这个异或值对（【1，N】的数+数组的数）进行分组处理，分别用一个数去异或两组不同的数，最终得到的两个数就是消失的两个数

4.参考代码

class Solution {
public:
    vector<int> missingTwo(vector<int>& nums) 
    {
        int n = nums.size();
        int tmp = 0;
        for(auto x : nums) tmp^=x;
        for(int i = 1;i<=n+2;i++) tmp^=i;
        int a = 0;
        int b = 0;
        for(int i = 1;i<=n+2;i++)
        {
            if(i&(tmp&(-tmp)))
                a^=i;
            else
                b^=i;
        }
        for(auto x:nums)
        {
            if(x&(tmp&(-tmp)))
                a^=x;
            else
                b^=x;
        }
        return {a,b};
    }
};

总结

本篇章总结了关于位运算的相关经典算法，其中有几道面试常见题，虽然简单，但思路巧妙