隐蔽通信(Covert Communication)论文阅读总结（以及正在尝试论文复现）

---

前言

本文准备先考虑隐蔽中通信经典的Alice, Bob, Willie三点模型, 总结出其中的经典套路

---

Covert Communications: A Comprehensive Survey

2023 IEEE COMMUNICATIONS SURVEYS & TUTORIALS

abstract

信息安全一直是无线网络中的一个关键问题。除了其他安全技术之外，隐蔽通信由于其高安全级别而成为无线网络安全的潜在解决方案。在隐蔽通信网络中，发射器通过引入随机性将传输的信号隐藏在环境或人工噪声中，以避免被看守发现。通过消除看守处传输信号的存在，可以比其他安全传输技术（即，无需注意到存在）更牢固地保护信息安全。由于具有良好的安全保护作用，隐蔽通信已成功应用于巨大的无线通信场景中。然而，其实际实施中仍然存在根本性挑战，例如随机性利用的有效性、合法用户的低信号干扰加噪声比等。在本次调查中，我们针对应用进行了全面的审查、解决方案以及隐蔽通信的未来挑战。具体来说，首先介绍了隐性原理和研究类别。然后，回顾了不同拓扑网络中的应用以及现有文献中有效的隐蔽技术。我们还讨论了未来网络中隐蔽通信的潜在实施以及公开的挑战。

简介

随着第五代（5G）和即将到来的第六代（6G）无线通信终端设备的不断发展，现代社会对信息传输的依赖越来越强[1]，[2]，[3]。除了无线通信的便利性之外，信息安全相关问题也至关重要且不容忽视[4]、[5]、[6]。围绕传输安全的研究从未停止。随着物联网（IoT）时代的到来，它变得更加重要[7]、[8]，其中传输的数据包含更多的个人信息，例如与用户健康相关的数据。此前，信息安全保护要么依赖于隐写术[9]，要么依赖于物理层安全（PLS）[10]、[11]，即应用层的消息加密或物理层的传输技术。对于消息加密，可以创建更复杂的用户名和密码，或者可以建立更复杂的加密协议来保护用户隐私。在PLS方面，它利用无线信道的固有属性以及编码或信号处理来提供安全保护[12]、[13]、[14]、[15]。这些技术可以有效地利用无线资源来实现更高的传输吞吐量，同时保证信息安全[16]。许多物理层资源可以联合优化以保护用户信息的隐私，这对于PLS[17]复杂度成本低的可靠传输来说是首选。因此，大量文献致力于改进PLS中的安全传输，以保证安全性，同时提供出色的传输性能，例如足够高的保密率。这些PLS方法可以利用功率分配、波束成形和极化来实现安全传输[18]。然而，隐写术和PLS只能以混乱的顺序隐藏信息，以防止窃听者解码接收信号中的合法信息[19]。然而，它们无法阻止恶意窃听者改进解码技术来获取传输内容，包括解决密码的分布式计算或高级信道状态信息（CSI）估计[20]，[21]。在这种情况下，一旦窃听者提高了解码能力，传输的安全性就无法得到保证。

最近，Bash 等人进行的里程碑式研究。揭示了安全传输解决方案，其重点是隐蔽通信的能力[22]。隐蔽通信隐藏了传输的存在，使其不被监管者检测到，这可以为发射器提供更高级别的安全性[23]。通过隐藏发射信号不被看守发现，发射器可以很好地保证其信息安全。这是因为，如果管理员不知道传输情况，他们就不会尝试解码信号中的内容。管理员会认为这些“信号”只是环境噪音，不会利用资源来解决它们。利用无线传输的隐蔽通信概念，将用户信息隐藏在“噪声”中，包括环境噪声或人为噪声，防止隐私泄露。结合其他技术，例如非正交多址（NOMA）或Turbo编码，隐蔽通​​信可以进一步帮助提高无线安全性，同时保证传输性能[24]，[25]。

通过利用多种传统技术来实现隐蔽传输，可以成功地向看守者“隐藏”所传输的信号[26]。首先，[27]、[28]、[29]中利用信道路径损耗和环境噪声来引入混乱并误导管理员，他们可能对决定发射机是否进行传输感到困惑。小规模衰落导致信道系数的随机性，这将导致守望者接收信号的随机变化[30]。郑等人。文献[31]证明，利用多径小规模信道衰落的优势，我们可以实现：1）在守望者检测中引入随机性，2）对多天线发射矩阵进行预编码以实现最大比值传输（MRT）[32]。在[33]中，Ta等人。分析了信道和噪声不确定性对 Willie 检测的影响，在考虑信道和衰落不确定性的同时推导了隐蔽吞吐量。此外，[34]、[35]、[36]中利用发射机、干扰器或中继器的功率变化来保证接收到的信号功率随机变化，这将导致管理员决策的不确定性发送器是否正在发送信息。通过控制传输信号的功率，可以将安全传输的信号隐藏在环境噪声或人工噪声中，这些噪声通常会不断振动以避免被检测到[37]。干扰或噪声的引入可以强调不确定性的总量，其中包括来自其他用户的环境干扰和人为噪声，因此系统可以容忍更强的传输信号[38]，[39]，[40]。同时，还可以利用高斯相关的信号来混淆管理员的检测[41]、[42]、[43]。与利用信道衰落和发射功率变化不同，发射机位置的变化也可以进一步增强隐蔽通信的隐秘性。周等人。减轻了[44]中的位置变化以欺骗发射机的传输。虽然位置随机性可以用来改变接收信号功率并使管理员对传输的存在感到困惑，但它有一个更严格的限制，即两个时隙之间的位置变化受到最大允许速度的限制。此外，可以通过调制传输信号来利用数字调制等随机选择模式来实现隐蔽通信[45]，[46]，[47]，[48]。表一总结了用于隐蔽通信的各种不确定性技术。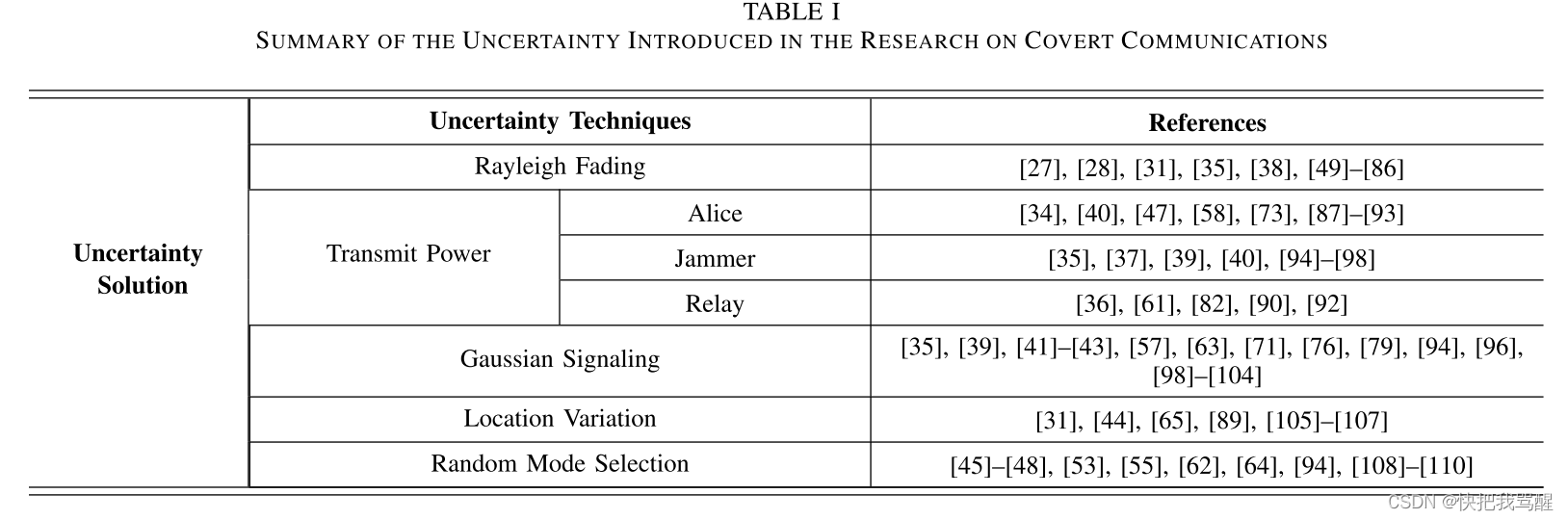
因此，隐蔽通信可以满足人们的普遍看法，即可以部署它来从根本上解决安全问题。通过将传输隐藏在环境或人工噪声中，隐蔽通信可以将通信的保密性提高到更深的水平[63]、[111]、[112]。隐蔽通信的典型好处可总结如下。

1. 部署简单且计算复杂度低：典型的隐蔽通信利用基本无线传输因素引入的不确定性，例如发射功率[95]、信道衰落系数[69]、位置变化等。这些因素可以由基本无线设备设计，易于配置和部署。无需高度依赖数学解决方案，例如大数据预测或基于机器学习的解决方案，只需基本设备即可实现隐蔽通信。
2. 主动安全防护：隐蔽通信可以主动隐藏传输信号。通过主动设计传输策略，例如发射功率的格式或人工噪声的分布，可以将敏感信号隐藏在噪声中，避免被守卫检测到，而不是防止窃听者接收后破解。每个传输指标，例如发射功率、无线信道和友好干扰器的分布[96]，都可以经过精心设计，以提高隐蔽通信的性能。
3. 全面的安全防护：利用隐蔽通信，安全信息可以隐蔽传输，不被恶意管理员发现。传输的信号被掩埋在不断变化且随机变化的环境噪声中，可能会在检测过程中迷惑典狱长。为了将隐秘信号隐藏在噪声中而不被注意到，发射功率往往较低，从而限制了传输范围。对于远距离隐蔽通信，可以部署中继来扩大覆盖范围[113]。因此，隐蔽通信可以防止恶意管理员检测到安全传输，从而提供全面的保护。
4. 现有技术的扩展：隐蔽通信的部署有望通过防止信息传输的存在被检测到来为信息传输提供全面的保护。不存在表明没有观察，也就没有裂缝。另外，结合现有的其他安全传输技术，如PLS或加密等，可以全面保证用户安全。因此，可以大大减少信息泄漏。

尽管隐蔽通信作为一种类似于PLS和加密的安全传输技术，但它与这两种技术有本质的不同[114]。通过将传输的信号嵌入噪声中，隐蔽通信可以实现更高的隐身概率，而不会被探测器的技术进步破解[115]。与旨在实现较低窃听率的PLS相比，隐蔽通信甚至不允许用户在被“注意到”的风险下安全，这可以极大地提高安全级别[116]。隐蔽通信也不同于加密，后者将私人信息的外观改变为上下文的另一个版本[117]、[118]。密码上下文主要以信息的随机顺序呈现，如果窃听者不知道密钥，则毫无意义。因此，可以通过加密来实现安全的信息保护。无需担心窃听者获得密钥，隐蔽通信可以为机密信息提供更好的隐蔽性。此外，上述三种基本的安全传输技术可以组合起来以获得更高水平的隐蔽性。我们在图 1 中展示了这三种安全传输技术的主要特征。隐蔽通信与其他两种技术之间的差异引发了对隐蔽通信网络进行全面研究综述的必要性和重要性。图1（a）中的发射机利用隐蔽通信的随机化技术引入不确定性来迷惑典狱长的检测。在图1（b）中，发射机利用信道的物理特性或借助人工噪声，通过最小化窃听者的信号与干扰加噪声比（SINR）来实现通信安全。通过图 1（c）中的加密，合法用户可以通过其密钥解码安全信息，而窃听者无法破解加密消息。因此，本综述旨在阐述隐蔽通信相关网络的物理原理基本概念、技术解决方案、典型应用以及性能分析。

尽管一些调查旨在说明隐蔽信道[119]、[120]、[121]、[122]，但现有文献中并未对隐蔽通信进行很好的调查。计算机网络协议中的隐蔽通道用于以隐藏或隐蔽的方式在两方之间传输信息。可以通过利用网络协议中的漏洞或以非最初预期的方式操纵传输系统来创建此类通道。隐蔽通信是指一种通信系统有意将其传输的信号隐藏在环境噪声或人为的不确定因素中，以避免传输行为被典狱长察觉，从而实现不被察觉的私密传输。因此，我们的调查对隐蔽通信的基础知识进行了详细的介绍和教程。此外，我们还展示了对隐蔽网络中广泛方案和应用的全面审查。本文的其余部分安排如下。在第二节中，我们介绍了基本的隐蔽通信模型，并叙述了与传统安全解决方案的差异。第三节列出了隐蔽通信的三个典型研究类别，展示了隐蔽通信的基本方法，并阐述了各个类别之间的差异。第四节展示了不同网络中隐蔽通信的可能应用场景。第五节对有效的隐蔽通信技术进行了全面的回顾和讨论，其中包括引入不确定性和保证隐蔽性的最新技术。在第六节中，我们讨论隐蔽通信潜在的新兴和未来应用和场景。最后，第七节指出了未来的问题和挑战。本文的主要主题如图 2 所示，表二列出了本次调查中的所有缩
写。

隐蔽通信的概念和机制

本节首先介绍隐蔽通信的发展历史。然后，我们演示并讨论三用户隐蔽通信模型的基本指标和主要考虑因素，以简要说明这个粗略的概念。此外，还讨论和比较了不同的安全保障策略。

隐蔽通信的简要历史

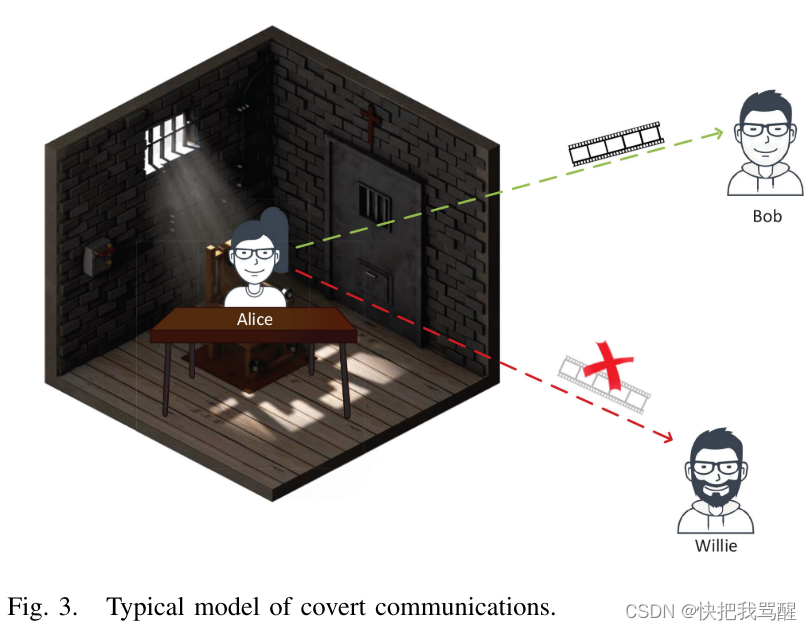
已经开发了各种技术和方案来提高隐蔽通信中的安全保护，这也可以称为信息隐藏。在不同的研究领域，安全拓扑有不同的要素。众所周知的基本隐蔽通信模型是囚徒问题，它由 Simmons 于 1983 年首次提出[123]。如图3所示，典型的秘密通信囚徒问题可以描述为Alice被囚禁并希望与Bob通信讨论她的越狱问题。然而，存在着一名典狱长威利，他不断监视环境信号，以防止爱丽丝计划逃跑。一旦典狱长对她的传输有任何合理的怀疑，爱丽丝的逃跑计划将被终止。典狱长并不关心传输的内容，任何正确的检测都会给爱丽丝带来极大的麻烦。因此，爱丽丝应该秘密地与鲍勃沟通，希望威利不会注意到。爱丽丝和威利之间的竞争可以从两个方面来描述。对于爱丽丝来说，她想隐藏她的传输不被威利检测到。对于Willie来说，他的目标是感知Alice是否发送了任何信息，这是一个二进制检测问题。

在1996年英国剑桥第一届“信息隐藏”国际研讨会上出现的隐蔽通信，也称为低**检测概率（LPD）**之前[124]，扩频技术被广泛用于将信息隐藏在噪声中，以防止信息泄露。防止在 20 世纪初发现安全消息。扩频技术将发射信号从其所需的带宽$B_r$扩展到更宽的带宽$B_w$，其中$B_r\ll B_w$，将发射信号的功率谱密度扩展至低于环境噪声，从而实现信息隐藏。尽管扩频技术在二战期间发展迅速并提供了隐蔽性，但其基本性能限制尚未得到分析。如果没有性能限制评估，我们就无法量化扩频所提供的隐蔽性性能，例如，系统的检测概率和特定风险概率内的最大隐蔽传输数据是不清楚的。因此，隐蔽通信的出现为信息隐藏研究提供了线索，特别是Bash等人提出的平方根定律（SRL）。 [22]。

经典的Alice-Bob-Willie Model

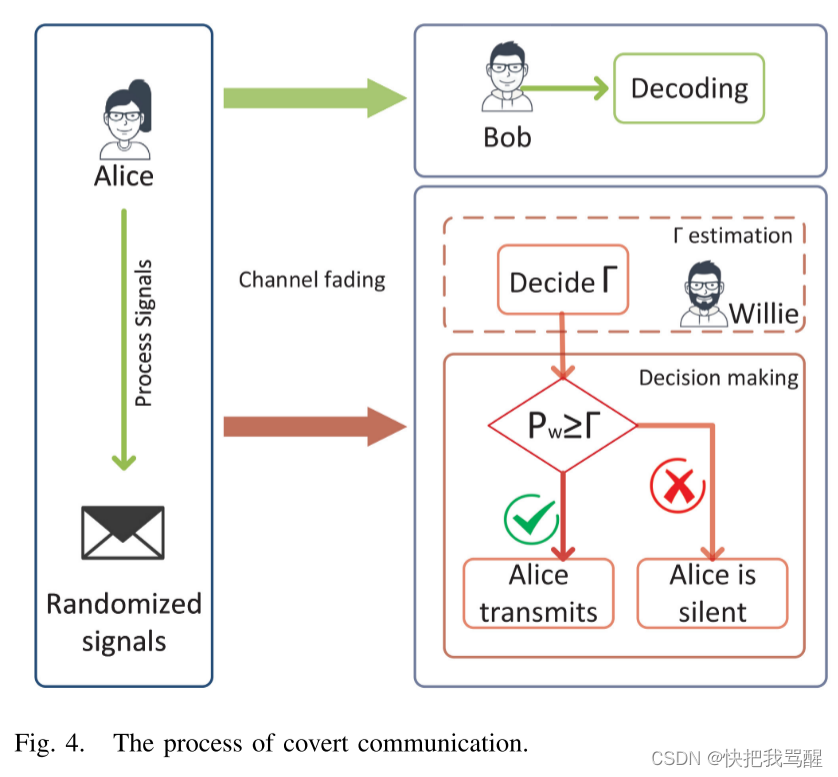
典型的隐蔽通信模型可以分为两个阶段，即Alice处的发送和Willie处的检测，如图3所示。一方面，Alice以${\pi }_1$的概率发送她的隐秘消息$x[i]$。以避免威利被发现并尝试提高她的传输性能。对于另一个 ${\pi }_0$ 概率，爱丽丝保持沉默。实际上，研究人员假设${\pi }_1={\pi }_0=0.5$ 以降低 Willie [31]、[64] 的检测概率。另一方面，威利尽力正确检测爱丽丝是否正在传输。

假设环境噪声可以描述为$n[i]$。根据Alice可能传输或不传输的可能条件，Willie的观察可以用两个假设来描述：
$$\begin{array}{l}{\mathcal{H}}_0:y_w[i]=n[i]\\ {\mathcal{H}}_1:y_w[i]=x[i]+n[i]\end{array}\text{\hspace{1em}(1)}$$

其中 ${\mathcal{H}}_0$ 表示 Alice 保持沉默，而 ${\mathcal{H}}_1$ 表示 Alice 正在传输。在典型的隐蔽通信中，Willie根据他的平均接收信号功率${\bar{P}}_w$来决定Alice是发送${\mathcal{D}}_1$还是保持沉默${\mathcal{D}}_0$，可以表示为
$${\bar{P}}_w=\frac{1}{n}\sum _{i=1}^n{\left|y_w[i]\right|}^2\underset{{\mathcal{D}}_0}{\stackrel{{\mathcal{D}}_1}{\gtrless }}\Gamma ,\text{\hspace{1em}(2)}$$

其中 $n$ 是 Alice 使用的信道数目来传输她的秘密消息，而 $\Gamma$表示 Willie 处的预设功率阈值。求和项 (2) 表示威利根据他的$n$个观测值的平均接收信号功率做出决定。威利认为，当 ${\bar{P}}_w\ge \Gamma$时，Alice 正在传输 ${\mathcal{D}}_1$，并且当 ${\bar{P}}_w\le \Gamma$ 时，Alice 保持沉默 ${\mathcal{D}}_0$。因此，预设的功率阈值至关重要，严重影响威利的检测精度。隐蔽通信的详细结构如图4所示。

威利可能会犯两种错误，即误报（FA）和漏检（MD）。 Willie 犯 FA 错误的概率 α = Pr ⁡ { D 1 ∣ H 0 } \alpha=\operatorname{Pr}\left\{\mathcal{D}_{1} \mid \mathcal{H}_{0}\right\} α=Pr{D1​∣H0​} 可以描述为 Willie 认为 Alice 正在传输而 Alice 保持安静。威利犯 MD 错误的概率 β = Pr ⁡ { D 0 ∣ H 1 } \beta=\operatorname{Pr}\left\{\mathcal{D}_{0} \mid \mathcal{H}_{1}\right\} β=Pr{D0​∣H1​} 表明威利认为爱丽丝在传输秘密消息时是安静的。 Willie的目的是通过适当设置功率检测阈值$\Gamma$来最小化总错误概率$\alpha +\beta$。

参考[22]，Willie 最优测试的错误检测概率可以描述为:
$$\begin{array}{rl}\alpha +\beta & =1-{\mathcal{V}}_T\left({\mathbb{P}}_0,{\mathbb{P}}_1\right)\\ & \ge 1-\sqrt{\frac{1}{2}\mathcal{D}\left({\mathbb{P}}_0\Vert {\mathbb{P}}_1\right)}\end{array}\text{\hspace{1em}(3)}$$
其中${\mathbb{P}}_1$定义为Alice发送信号时Willie观测值的概率分布，${\mathbb{P}}_0$表示Alice保持沉默时Willie观测值的概率分布。${\mathcal{V}}_T\left({\mathbb{P}}_0,{\mathbb{P}}_1\right)$是${\mathbb{P}}_0$和${\mathbb{P}}_1$的总变化距离。应用平斯克不等式，即${\mathcal{V}}_T\left({\mathbb{P}}_0,{\mathbb{P}}_1\right)\le \mathcal{D}\left({\mathbb{P}}_0\Vert {\mathbb{P}}_1\right)$，可推导出(3)。 $\mathcal{D}\left({\mathbb{P}}_0\Vert {\mathbb{P}}_1\right)$ 是 ${\mathbb{P}}_0$ 和 ${\mathbb{P}}_1$ 之间的相对熵。

当检测阈值$\Gamma$设置为最优值时，即可获得最优检测，其中最优功率检测阈值 ${\Gamma }^{\ast }$可推导为
$$\frac{{\mathbb{P}}_1}{{\mathbb{P}}_0}\stackrel{{\mathcal{D}}_1}{\underset{{\mathcal{D}}_0}{\gtrless }}1.\text{\hspace{1em}(4)}$$
然后，可以通过（2）、（3）和（4）的组合得出最佳功率检测阈值${\Gamma }^{\ast }$[22]。

由于爱丽丝和威利之间不知情，所以可以进行秘密通信。 Willie 和 Alice 之间的不知晓是相互的，即 Willie 不知道 Alice 何时传输或实时 CSI，Alice 也不知道 Willie 或他的 CSI 设置的检测阈值。然而，Alice 需要保证 Willie 处的总检测错误概率超过 $1-ϵ$ ，即 $\alpha +\beta >1-ϵ$。因此，Alice 隐蔽通信的典型假设是 Willie 将其检测阈值设置为最优值 ${\Gamma }^{\ast }$，这样当 Willie 不将检测阈值设置为 ${\Gamma }^{\ast }$ 时，可以保证更高的隐蔽性。

基于 Willie 的最优检测，Alice 可以联合优化她的参数，例如发射功率、传输速率或预编码向量，以获得更好的性能。

与其他安全技术的区别

我们主要比较隐蔽通信与PLS、密码学和扩频的区别，如表3所示。

1）物理层安全：一般来说，PLS可以通过物理层而不是上层的信令或信道编码联合利用无线信道的特性（例如衰落）来实现。与隐蔽通信不同，PLS主要是防止窃听者解码而不是获取安全数据。 PLS的优点之一是它不需要合法用户的超强计算能力。 PLS的主要目的是降低窃听者的SINR，同时保证合法接收者的传输性能。然而，在PLS系统中，预编码向量或波束成形矩阵的设计通常假设窃听者的CSI在发射机处可用。尽管大量研究都集中在 CSI 估计上，但这是不切实际的。此外，窃听者解码能力的提高也会对PLS造成威胁。

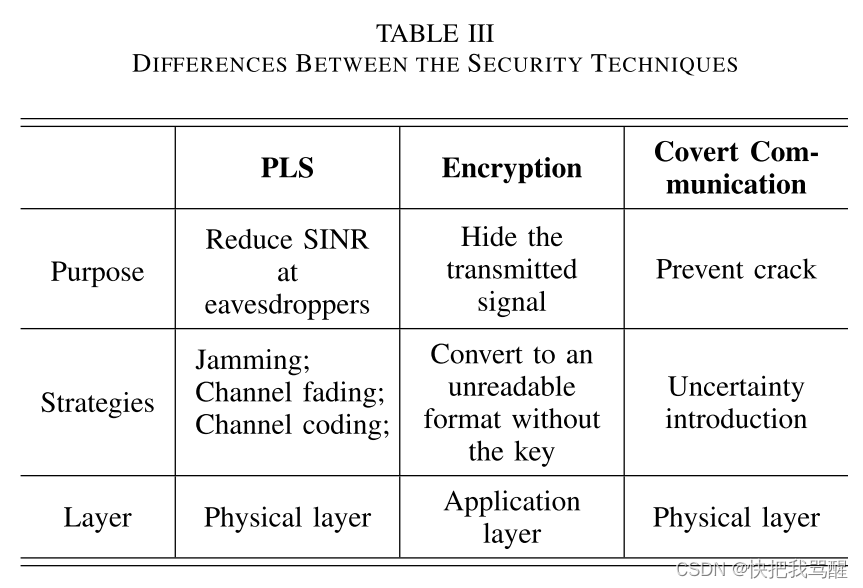
2）密码学：对于密码学来说，传输的数据被转换为不可读或无意义的格式，并且只能通过特定的密钥来解密，其中包括公钥/私钥解密或苛刻功能解密。公钥/私钥系统可以验证用户的身份，而哈希函数可以将消息转换为一组其他不可破解的数据格式。密码学的主要目的是保护传输消息的内容，窃听者无法解读加密消息的内容。然而，当量子计算或其他超级计算技术进一步被窃听者开发和应用时，密码技术将面临重大威胁。因此，加密的消息仍然存在被发现的风险。

3）扩频通信：这是另一种类似于隐蔽通信的技术，它可以保护传输行为而不是隐藏传输信号的内容。实现信息隐藏需要消耗较多的频率资源。具体而言，扩频通信利用比所需的Br更宽的带宽Bw，即Bw Br，将秘密消息传播到环境噪声中。文献证明扩频可以为无线通信提供安全性[125]、[126]、[127]。然而，目前还没有关于它的详细分析结果，例如安全信息量、检测概率、错误检测概率等。尽管扩频在20世纪初期已经在军事上得到了很好的应用，但由于缺乏可靠的理论性能限制，仍然会导致安全性的丧失。

隐蔽通信的研究范畴

隐蔽通信的核心概念是隐藏传输的信息不被典狱长检测到[128]。自从 Bash 等人提出里程碑式的结果以来。在[22]中说明了性能限制，隐蔽通信相关的研究已经蓬勃发展。接下来的隐蔽通信相关研究主要集中在理论性能限制、编码方案和实际场景三类。性能极限的理论研究主要是在信息论层面推导在特定的低检测概率下能够秘密传输给接收者的信息量。第二个分支侧重于通过他们提出的编码方案实现信息限制，并导出所需的密钥长度。对于第三类，研究人员旨在将隐蔽通信应用到实际场景中，并借助其他技术来提高隐蔽通信的性能。在本节中，我们详细讨论这三个研究方面，并提供文献综述来展示每个类别。

平方根定律相关工作

Bash 等人取得的突破。展示了具有加性高斯白噪声（AWGN）的隐蔽通信网络的 SRL [22]，它阐明了隐蔽通信的性能限制。在这种情况下，考虑一个典型的隐蔽通信模型，包括发送器 Alice、接收器 Bob 和典狱长 Willie。具体来说，Bash 等人。研究了 AWGN 信道模型中的平方根极限，在噪声功率已知和未知的两种条件下，接收器 Bob 处的功率方差为 σ2 b > 0，Willie 处的功率方差为 σ2 w > 0。 Alice 与 Bob 通信有 n 个并且共享秘密就足够了。考虑到当 Alice 保持沉默时，Willie 处观测到的总功率为 σ2 wn，因此当 Alice 进行传输时，n 个信道使用的总接收​​功率将增加并引起怀疑。巴什等人。理论上证明，当解码错误概率极低时，Alice 可以可靠地传输 o(√n) 位，其中 o(f(n)) 表示上限。表示 Willie 处的任意小错误检测概率，以保证当 Alice 处的 σ2 w 未知时，α + β ≥ 1 − 。他们进一步证明，如果 Alice 知道 σ2 w 的下界，则在 n 个通道使用内，并且任意小的满足 α+β ≥ 1− 的情况下，她可以传输的信息量为 O(√n)，其中 O(f(n) ) 表示渐近上限。此外，还得出了一个富有洞察力的结论，即当n→∞时，每个通道的传输信号等于0，即limn→∞ O(√n)n→0。

在上述初步工作之后，进一步进行了大量与隐蔽限制相关的研究[97]，[129]，[130]，[131]，[132]，[133]，[134]，[135]。例如，Bash 等人。在[134]中，在一个更实际的假设中进一步研究了SRL，即典狱长不知道确切的传输时隙。已经证明，如果 Alice 在 n 的 T(n) 个时隙内传输超过 O(min{n logT(n) 1 2 , n}) 位，则 Alice 的传输很有可能被典狱长检测到。渠道用途。基于[134]中相同的系统模型，Goeckel 等人。在[135]中推导了当典狱长对环境噪声没有预先了解时可以秘密传输的信息限制。他们证明，在同步条件下，Alice 无法在 T(n) 个时隙之一内可靠地传输超过 ω( n logT(n)) 位，其中 ωf(n) 表示渐近下界。在Willie不知道Alice传输的码字边界是什么时候的异步信息的情况下，他们还证明了Alice在使用n个信道和一个常数的情况下仍然无法传输超过 ω(  n logT(n)) 位的信息发射功率。上述结果也限制了Alice选择T(n)个时隙中的几个时隙进行传输的情况。与[22]中典狱长拥有完整的信道统计知识的假设不同，Sobers 等人。文献[97]证明，在最佳和非最佳条件下，发射机可以在友好干扰器的帮助下，在 n 个通道中秘密且准确地向接收机传输 O(n) 位，而不会被 Willie 检测到。文献[97]中的结果是在消除了 Willie 检测器的所有约束的情况下得出的，包括信道统计模型、码字长度 n、Alice 码字的分布、干扰分布、Alice 可能的传输时间，以及与爱丽丝的距离。

上述所有研究都是基于 AWGN 信道假设。对于其他渠道，布洛克等人。在[136]中探讨了玻色子通道和经典量子通道上隐蔽通信的基本限制[137]。他们推导出单模玻色子有损热通道模型的SRL，适用于光环境、射频（RF）通道和微波等量子场景中的隐蔽通信。玻色子通道中 SRL 的详细表达是在 Willie 受到量子限制的假设下得到证明的。然后，Sheikholes 等人。 [137]证明了SRL可以在无记忆经典量子通道中实现。

隐蔽通信的编码方案

在[22]中开创性的SRL研究之后，进行了许多工作来建立Alice和Bob之间的编码方案或共享密钥长度[138]、[139]、[140]、[141]、[142]。他们的主要目标是通过设计合适的编码方案[143]、[144]、[145]、[146]、[147]、[148]在实际场景中实现SRL。在[138]中，Wang等人。一致认为 SRL 可以容纳许多离散的无记忆通道。他们在以下假设下推导了最大传输信息的缩放常数表达式，其中包括： 1）Willie 对信道信息有相同的观测； 2）Alice和Bob之间的共享密钥足够长。此外，爱丽丝在关闭后会发送“关闭”符号。遵循涉及“关闭”符号的字母表的相同假设，Cho 和 Loe 在[149]中研究了 K 个用户对的离散无记忆干扰信道下的隐蔽通信。他们证明了最优方案是将干扰视为噪声的点对点相关方案。此外，他们还分析了每个用户对中密钥所需的最小长度，结果为0。先前的工作一致认为，仅在n个信道上使用O(√n)位信息就可以秘密传输。指数计算复杂度的条件。张等人。在[150]中提出了一种编码方案，可以保证隐蔽容量，同时保持与信道使用n呈多项式相关的计算复杂度。他们应用系统化的里德-所罗门码来消除编码内容的依赖性，这也会给威利带来不确定性。于等人。研究了[151]中无限块长度隐蔽通信的最大信道编码率。他们应用高斯随机化编码方案来实现对总变异距离的更方便的分析。推导出具有输入约束的随机编码方案的最大和平均错误概率。此外，他们还比较了得出的可实现范围和当前结果。在[152]中，Xu等人与其他工作不同，提出了一种利用非零均值高斯序列的方案，其中他们用隐形二进制位调制均值。基于所提出的方案，对隐蔽性能和传输性能进行了分析。

不同类型 Willies 的实际场景

根据wardens的模式，隐蔽通信的典型应用可以分为三类，即单Willie、多Willie和主动Willie。人们提出了许多方案来保证在每种模式下针对 Alice 上设置的不同障碍的隐蔽通信的隐秘性，其总结如表 IV 所示。

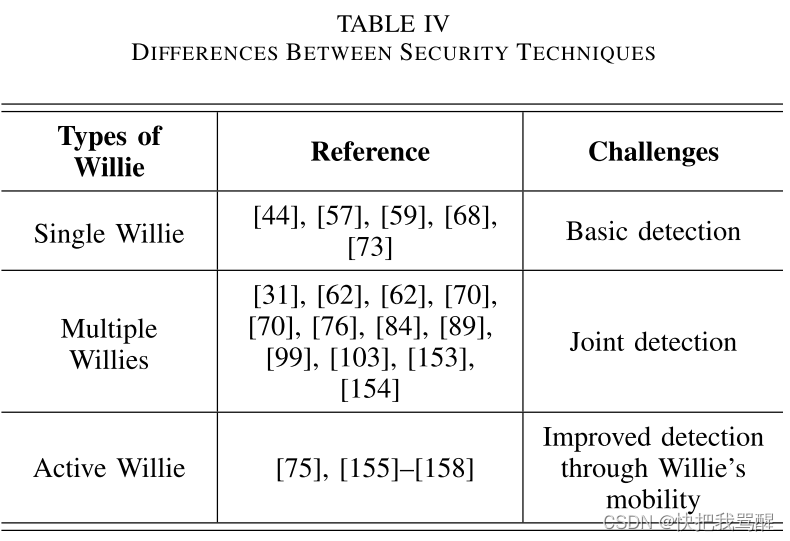
Single Willie:

(典狱长是warden的汉语翻译)
在大多数典型的隐蔽通信模型中，都存在发送者、合法接收者和被动的恶意守护者[59]。当只有一名典狱长时，我们可以利用不同的技术来迷惑威利，使其无法发现传输信息。特别是，这些技术可以利用小规模信道衰落或利用发射功率变化。这些解决方案会给典狱长接收到的信号带来不确定性。周等人。文献[44]考虑了隐蔽通信的无人机（UAV）轨迹设计存在位置估计误差，这会给隐蔽通信带来不确定性。 Chen 等人在 [68]、[159] 中利用了小规模路径损耗随机性。迷惑单个典狱长，使其无法成功检测到爱丽丝的传输。然后，陈等人。在[57]、[160]中进一步研究了有限块长度范围内的单典狱长隐蔽通信，这在物联网相关网络中是实用的。 Shahzad 等人假设传输的信号样本遵循复杂的高斯分布。在[73]中，这可以欺骗威利关于秘密通信的信息。

Multiple Willie:

当多个监护人可以结合他们的观察结果并做出相应的结论时，错误检测概率将急剧降低[99]，[153]，[154]。这对秘密通信构成了重大威胁。索尔塔尼等人。在[89]中考虑了单个典狱长和多个合作典狱长场景下的秘密通信。借助友方节点产生干扰扰乱威利斯，Alice 可以保证传输的隐蔽性。随后，Sheikholeslami等人提出了利用多个中继进行长距离隐蔽通信，对抗多个具有固定位置的Willie的策略。在[103]中。郑等人在[31]中研究了涉及多个位置不固定的 Willies 的秘密通信，其中 Willies 的位置遵循均匀分布。他们研究了多天线Alice在集中式天线系统（CAS）和分布式天线系统（DAS）下的影响。继上述工作之后，陈等人。进一步考虑了无人机辅助 LPD 中与多个管理员的秘密通信[84]、[161]，其中合作管理员分布在二项式点过程位置上。最近，马等人。在[76]中，将多管理员隐蔽通信网络扩展到有限块长度的体系中，其中管理员的随机分布遵循泊松点过程。在[70]和[62]中，讨论了远距离秘密通信。为了保证通信性能，长距离传输需要更高的发射功率，这会带来更高的被发现风险。如前所述，多个 Willies 可以相互协作，共同做出 Alice 传输的检测结果。福鲁泽什等人。在[70]中，利用中继克服了长距离隐蔽通信的障碍，同时也阻止了不受信任的中继解码源信息。在[62]中，Rao 等人。在动态中继选择方案的帮助下，进一步检查了针对多个典狱长检测的秘密通信。

Active Willie

在大多数现有研究中，恶意威利被假设停留在固定位置，这低估了其检测能力。实际上，威利可以在观察过程中相应地改变他的检测位置[75]，[155]。在检测到活跃的威利期间，他可以调整他的决策规则或改变他的检测位置。在[156]中，Forozesh 等人。当威利在爱丽丝的估计位置不完美时，考虑了更实际场景中的秘密通信。此外，他们在友好的干扰器上配备了多个天线，通过在零空间中向合法接收器进行波束成形来消除干扰，从而提供更高的隐蔽传输速率。他们还利用 3 维 (3D) 波束成形天线阵列提高了传输性能。刘等人。在[157]中发现，如果Alice不知道主动Willie的先验知识，她就无法隐藏她的传输，而Willie可以根据检测结果的趋势动态改变他的检测位置。此外，Alice可以随机化她的传输调度，其中传输概率应低于阈值，以实现针对主动Willie的隐蔽通信。 Tahmasbi 和 Bloch 在[158]中提出了一种动态协议，允许 Alice 和 Bob 交换主动典狱长无法获得的密钥，以实现隐蔽通信。

隐蔽通信的应用

通过巧妙地将隐秘传输的信号隐藏在噪声中，机密信号可以秘密地传输到预期的接收者，同时防止恶意典狱长检测到它们的存在。 AWGN信道的理论平方根极限在[22]中得到了很好的论证和证明，打破了隐蔽通信研究的坚冰。在本节中，我们对不同类型网络中隐蔽通信的主要应用进行了全面的回顾，如表五所示。隐蔽通信的典型应用包括认知无线电（CR）、NOMA、超可靠和低延迟通信（URLLC）、物联网网络、无人机辅助网络、远程网络和卫星网络，其简要结构如图5所示。

认知无线电中的隐蔽通信

CR正在作为提高协作频谱效率的关键技术而发展。在CR网络中，无线资源被动态规划以利用最优或最可用的频谱以避免用户之间的干扰，这可以简单地关注动态频谱管理来解决未来网络中频谱资源的短缺[175]。然而，由于其动态特性和结构，恶意窃听者可能存在攻击的可能性，这也是由多个设备的访问可用性造成的。通过将隐蔽通信应用于CR网络，我们可以同时保证信息隐秘性和频谱效率[105]。基本的 CR 隐蔽网络如图 6 所示。

廖等人。 [61]提出了一种新颖的基于生成对抗网络的功率分配（GAN-PA）方案来保护 CR 网络中的隐蔽通信。在 GAN 模型中，一台生成器同时传输真实和虚假样本，以误导典狱长从虚假样本中检测出真实样本。他们考虑了辅助发射机辅助 CR 隐蔽网络，其中贪婪中继可以使用频谱资源将其非法消息传输到接收机。部署管理员来检测中继器是否传输从发射器接收到的合法消息或传输自己的非法消息。他们利用博弈论来分析和优化接收端所有通道的传输速率以及典狱长端的检测错误概率。他们提出的 GAN-PA 方案可以获得快速收敛的近乎最优的功率分配解决方案。遵循类似的情况，Chen 等人。 [49] 研究了 CR 网络中的隐蔽通信，并考虑了多个辅助发射机。提出了三种调度方案，即面向速率、面向链路和面向公平的次用户调度。选择两个辅助发射器将秘密消息转发到辅助接收器，同时避免被典狱长检测到，分别作为中继器和干扰器。基于隐蔽传输速率、接收信噪比（SNR）和公平性的最大化，同时保持威利错误检测概率，导出了三种传输策略。与前述的中继辅助模型不同，Xiong 等人。在[101]中研究了隐蔽通信网络中的认知干扰器，它可以感知环境以感知Alice的传输，然后决定其干扰策略。在Alice发送的n个块中，干扰器观察前m个块，然后基于观察Alice的沉默或保持沉默，在其余n-m个块期间发送干扰信号。在认知干扰器的帮助下，他们最大限度地提高了隐蔽传输速率，同时将错误检测概率保持在其限制之上。在[162]中，Xu等人研究了波间认知无线电，其中研究并优化了频谱感知和数据传输的块长度以最大化有效吞吐量。

NOMA 中的隐蔽通信

NOMA作为未来网络的一种潜在技术，可以让更多的用户利用相同的频谱资源，从而显着提高频谱效率。以功率域NOMA为例，基站（BS）将多个用户的信息通过叠加编码（SC）在同一频段组合在一起发送，然后用户可以通过以下方式接收和相减自己的信号：连续干扰消除（SIC）。在NOMA中，发射机将较高的发射功率分配给较弱的用户，即信道条件较差的用户。由于每个用户都可以访问其他高功率用户的信息，因此信道条件较差的用户存在信息泄露的风险。因此，信息安全对于 NOMA 网络至关重要。与PLS不同，将隐蔽通信应用于NOMA网络可以实现最基本的保护，即隐藏传输信号的存在而不被检测到[34]，[90]。隐蔽的 NOMA 网络如图 7 所示。

陶等人。在[54]中考虑了通过随机化发射功率实现的下行NOMA系统中的隐蔽通信。在这封信中，Alice 在 NOMA 网络中与两个合法用户进行秘密通信，其中弱用户覆盖强用户。出于电池寿命的考虑，他们利用能量收集干扰器来辅助秘密通信。该方案有两个阶段[54]，即能量收集阶段和信息传输阶段。干扰信号和微弱的公共信息在整个信息传输阶段都会被发送，而隐蔽信号则偶尔会被发送。他们优化了隐蔽信号的发射功率，以最大化隐蔽传输速率，同时限制最小检测错误概率和连接中断概率。 NOMA 网络中的隐蔽通信也在 [52] 中进行了研究，其中 Wang 等人。采用信道反转功率控制(CIPC)来实现隐蔽性。在这个系统中，公众用户和Bob共同合作，欺骗典狱长检测到Alice的传输。 Alice按照NOMA以0.5的概率向Bob和公共用户发送消息，而当她保持沉默时只向公共用户发送消息。与此同时，公共用户发送带有截断的 CIPC 的人工噪声来迷惑威利并帮助爱丽丝进行秘密通信。 Jiang等人研究了NOMA系统中的设备到设备（D2D）隐蔽通信。在[51]中。由于电池限制，D2D通信容易受到恶意攻击，通过隐蔽交易可以提高安全性。在本文中，他们利用非隐蔽 D2D 用户以及 BS 作为友好干扰器来协助 D2D 设备进行隐蔽通信。 D2D发送器借助遵循复杂高斯分布的信道衰落秘密地向D2D接收器发送信号。通过优化隐蔽发射功率，可以最大化 D2D 链路上的平均传输数据速率，同时将错误检测概率保持在其约束下。在[171]中，Mallikarachchi 等人。研究了多跳无人机网络中的多个中继，提出了在某些特定约束下实现隐蔽通信的传输方法。张等人。研究了 NOMA 网络中的隐蔽传输，并考虑了 [163] 中的信道估计误差。

URLLC中的隐蔽通信

为了实现更好的传输性能并降低通信延迟，URLLC被提出来实现5G网络的超可靠和低延迟性能，其中短包传输对于实现URLLC要求非常重要。为了保证可靠性并减少延迟，信息应通过短数据包传输。然而，对于无线通信来说，其安全性仍然是一个关键问题，这可以通过利用有限块长度网络的隐蔽通信来解决[42]。与传统的无限块长度通信不同，香农理论在有限块长度网络中不成立，这对于5G网络极其重要。在传输性能和隐蔽性方面，需要同时考虑解码错误概率和信息泄漏概率[56]。

在[109]中，Xu等人。研究了有限块长度网络中典型的 Alice-BobWillie 隐蔽通信模型，其中信道选择是随机的。本文分析了有限块长条件下Willie处的相对熵和Bob处的译码错误概率。在Willie端检错概率的约束下，通过适当调整信道使用概率，使Bob端的误码概率最小化。然后，马等人。研究了[164]中的功率控制方案，以在有限块长度的情况下提供隐蔽通信。这封信研究了短数据包机制下传统和集群 CIPC 方案的隐蔽通信。在CIPC系统中，Alice的发射功率与她和Bob之间的信道系数成反比。截断方案表明，除非信道增益系数超过预设值，否则Alice不会发送任何信号。通过这两种方案，在Willie处的检测错误概率大于阈值的约束下，通过调整功率控制参数，可以最大化有限块长度有效的隐蔽吞吐量。此外，无人机Alice的部署是在[165]的时间不容忍的隐蔽通信网络中设计的。在本文中，周等人。分析了无人机 Alice 的悬停位置，得出最佳位置，从而在 Willie 处获得更高的检测错误概率，并提供足够的有效吞吐量。得到无人机的最优发射位置后，发射功率和悬停高度也在上述约束条件下得到优化。严等人。 [102]中还讨论了具有固定或随机发射功率的有限块长度无线网络中的隐蔽通信。他们讨论了块长度对 Willie 的检测和 Alice 的传输的影响，然后得出最佳值。通过检测阈值和传输信息量相对于块长度的单调性分析，他们得出结论：最优块长度应该达到最大值，以获得最大的传输信息。

IoT网络中的隐蔽通信

物联网作为下一代移动网络的一场革命而出现，无处不在的设备可以在同一网络内连接。这些与每个人相关的设备可以传输大量的私人信息，包括监控视频、用户轨迹信息、个人健康数据等。然而，无线通信始终面临着被窃听和隐私泄露的风险。许多技术被用来处理信息泄露，包括 PLS 和加密。此外，还可以利用隐蔽通信来实现物联网网络中的信息安全，如图1所示。 8、由于其信息隐藏的优点。物联网网络中的设备通常尺寸较小且电池电量低，这导致无法进行复杂的编码[74]。因此，在物联网网络中应用隐蔽通信不需要很高的计算能力[112]，[176]。

王等人。在[166]中利用隐蔽物联网网络中不正确的高斯信令来提高隐蔽传输速率。在本文中，物联网节点希望借助基站及其相关接收器形成的频谱庇护所来秘密向鲍勃传输数据。他们证明，与仅利用适当的高斯信令相比，同时利用不适当的高斯信令和干扰可以提高隐蔽传输速率。在[66]中，胡等人。 Bob 在 CSI 不知情的情况下调查了 IoT 隐蔽通信网络。采用CIPC方案来保证Bob的信号功率恒定，而不需要知道他和Alice之间的CSI。他们导出了最佳功率控制参数，以最大化隐蔽传输容量，同时保持总错误检测概率高于其要求。此外，他们还证明增加 Bob 和 Willie 的噪声不确定性并不能提高隐蔽性能。高等人。 [108]考虑了长距离场景中的物联网隐蔽通信。与传统的仅考虑一个中继的远程无线中继辅助通信不同，该物联网网络中部署和选择了多个中继。他们比较了随机中继选择方案和高级链路选择方案下的隐蔽无线物联网通信。他们证明，与随机中继选择方案相比，优越链路选择方案可以在相同约束下提供更高的隐蔽容量。大多数现有的隐蔽通信方案都是在 AWGN 信道下进行的，而 Sodagari 在 [167] 中研究了 Nakagami 衰落下物联网网络中的隐蔽通信。刘等人。在[107]中考虑了太赫兹（THz）下的隐蔽物联网通信。他们利用镜面反射表面来协助物联网网络中的隐蔽通信。除了理论研究之外，雪莱等人。在[168]中对硬件木马进行了秘密通信，他们在硬件平台上进行了实验。结果表明，由于其他物联网设备的发射功率较低，通过在合法典狱长处明智地观察和检测，可以检测到恶意硬件木马的发射。

无人机辅助网络中的隐蔽通信

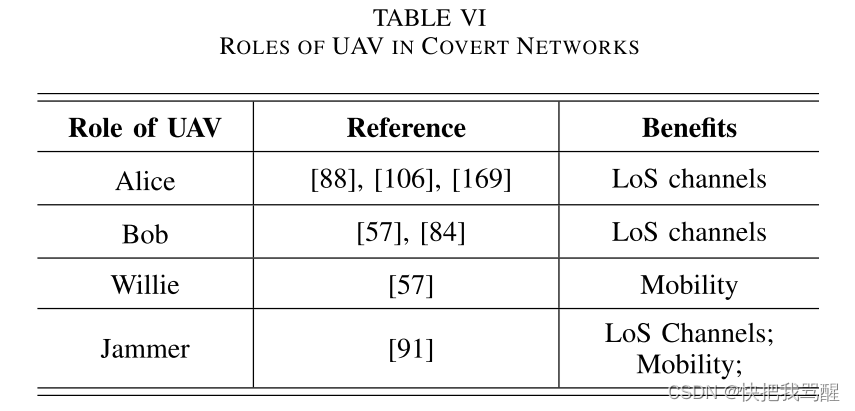
无人机具有高机动性和易于部署的特点，可以实现网络配置的灵活性。此外，在无线通信中使用无人机可以受益于空对地链路中高概率的视距（LoS）信道的传输性能。虽然LoS信道可以提高通信性能，但由于无线信号的开放接入特性，也容易受到恶意窃听者的攻击。与传统的安全解决方案不同，可以采用隐蔽通信来有效保护无人机相关的传输。根据无人机的功能，与无人机相关的通信可以分为四类，即无人机作为Alice、Bob、Willie和干扰机[78]，总结在表六中。

严等人。在[88]中研究了以无人机为爱丽丝的网络中的秘密通信。在本文中，无人机Alice想要向地面Bob传输秘密信号，并试图避免被Willie检测到。他们根据向鲍勃的传输和向威利的隐蔽性在六种情况下分析了爱丽丝飞行位置的影响。他们证明，尽管就近的可能传输位置可以带来较高的传输速率，但对于隐蔽性保护而言，它并不总是最佳位置。在[169]中，Hu等人提出了通过波束扫描检测可疑无人机传输的策略。他们将可疑的空中区域划分为几个扇区，并利用波束形成增益来提高检测精度。他们得出了最佳的检测扇区数量，以最大限度地减少错误检测概率。对于像Alice这样的无人机进行数据采集的隐蔽通信，Jiang等人。 [106]设计了多用户网络中无人机的轨迹和资源分配策略。他们共同设计了每个用户的时间分配、轨迹和发射功率，以最大化平均隐蔽传输速率，同时保证典狱长的错误检测概率大于约束。与上面讨论的作品不同，陈等人。文献[84]研究了无人机作为接收器时的无人机辅助隐蔽通信。通过利用其移动性，无人机Bob可以调整其悬停位置以实现更好的传输性能。他们推导了 Bob 的最佳悬停位置以及其他资源分配策略，以最大化隐蔽传输速率，同时保持错误检测概率高于其约束。梁等人。文献[91]研究了无人机作为干扰机工作的场景，无人机干扰机可以很容易地部署来干扰典狱长的检测。在无人机干扰器的帮助下，他们分析了 AWGN 和 Nakagami-m 衰落下的隐蔽通信性能。无人机的移动性也可以被用来充当恶意威利或中继。陈等人。在[57]中研究了威利和中继都是无人机的场景。隐蔽通信是在最坏的情况下，无人机威利可以改变他的探测位置，而且通信距离很远，需要中继的帮助。在这种最坏的情况下，他们提出了一种满足隐蔽性和传输性能要求的实现隐蔽通信的方案。

远程网络中的隐蔽通信

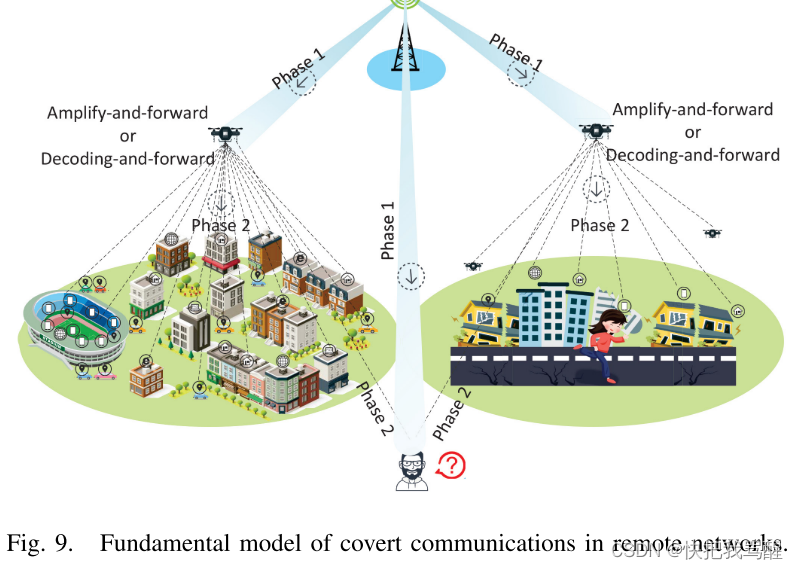
毫无疑问，无线通信可以给每个人的日常生活带来极大的便利。然而，无线通信的质量会受到信道衰落的影响或降低，这在长距离传输中变得更加严重。虽然可以通过提高发射功率来扩展传输范围，但另一方面也会带来严重的安全风险[171]。因此，可以部署中继来提高传输性能[82]、[177]。此外，借助隐蔽通信[178]、[179]可以进一步保证中继辅助网络的安全性，如图9所示。

在[71]中，Wang等人。通过探索信道不确定性，在中继辅助的长距离网络中进行隐蔽通信。他们假设信道系数遵循瑞利衰落，传输信号遵循复高斯分布。 Bob 和 Willie 均考虑了信道不确定性。在中继的帮助下，证明了 Alice 可以使用 n 个通道传输 O(n) 位。孙等人。在[36]中研究了全双工（FD）和半双工（HD）模式下的中继辅助隐蔽通信。他们证明，通过联合切换FD和HD之间的中继模式并优化发射功率，隐蔽通信可以获得更好的隐蔽传输速率性能。为了进一步提高通信性能，Lv 等人。在[92]中利用多天线中继来提高隐蔽传输速率。提出了两种波束赋形相关方案，即最大比传输（MRT）方案和随机波束赋形方案，它们通过Relay和Bob之间的CSI是否可用来区分。他们证明，与随机波束形成方案相比，MRT方案在相同检错概率约束下可以实现更高的隐蔽传输速率。 Hu等人在[28]中研究了恶意中继也可以用于协助远程传输。中继是贪婪的，并尝试使用公共资源将其自己的消息与来自源的中继消息一起传输。他们提出了速率控制和功率控制两种方案来实现非法隐蔽通信检测。事实证明，该速率控制方案能够实现较高的有效隐蔽传输速率。在[27]中，王等人。研究了更长范围内的隐蔽通信，这需要多个中继来多跳消息。本文提出了一种通过多个地面节点实现隐蔽通信以防止无人机管理员检测的方案。由于中继采用解码转发模式，无人机可以联合检测隐蔽传输。这会带来被合法典狱长发现的严重风险。他们设计了发射功率、编码率和跳频数，以最大化保密吞吐量，同时限制 Willie 的联合错误检测概率。当有更多可用中继时，甚至可以通过选择具有最佳CSI的中继来优化隐蔽通信。苏等人。在[55]中，利用最优中继设计了中继选择方案。该方案有效降低了错误检测概率，并且在相同隐蔽性约束下，还可以提高平均隐蔽传输速率。在[170]中，胡等人。联合优化Alice和无人机中继的发射功率以及无人机的悬停高度，以最大化隐蔽吞吐量，同时保持Willie的错误检测概率高于最大允许约束。

卫星网络中的隐蔽通信

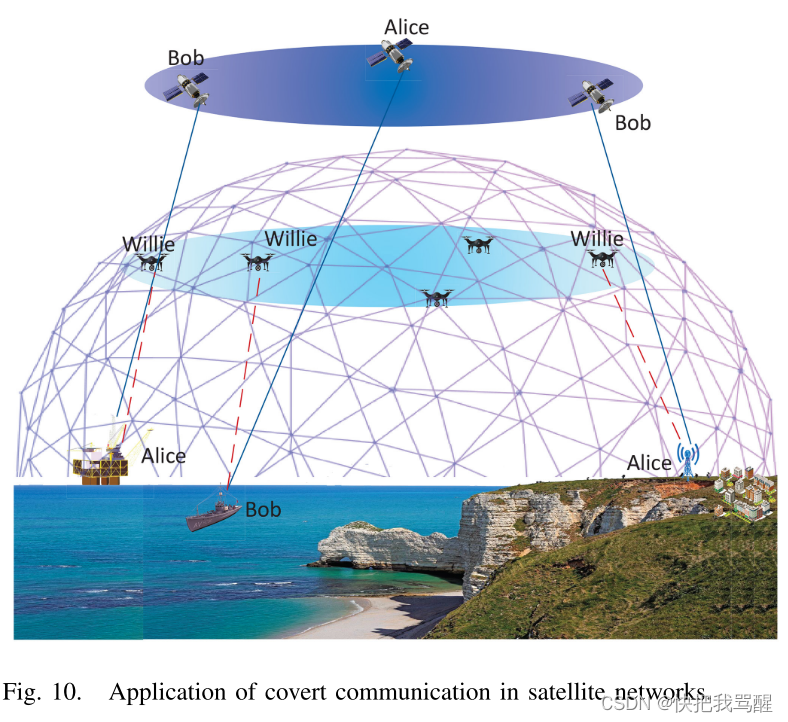
为了实现更广泛的无线通信范围而不受地理区域的限制，卫星因其先进的能力成为首选[180]。卫星通信因其通信距离远、可靠性高、多址接入等先进特点而受到广泛关注。卫星通信可以提供极其广泛的覆盖范围。此外，它还提供高可靠的链路，不会受到地质灾害中BS破坏的影响。此外，卫星通信可以以低成本实现广播和在不同地点的多址接收。尽管卫星通信可以利用多种技术来保护传输信息的安全，但由于无线广播的开放性和覆盖范围广，仍然存在很高的被窃听风险。如图10所示，将隐蔽通信应用于卫星网络可以防止Willie检测到Alice的传输，进一步避免信息泄露。然而，如何在保证传输质量的同时实现隐蔽性仍然具有挑战性。

康等人。在[172]中比较了三种典型NOMA方案的隐蔽性性能。本文中，多个公共用户中的一个地面Alice将上行信息传输给卫星Bob，同时避免检测到无人机Willie。隐蔽消息在公共信息的掩护下传输，两者通过稀疏码多址、多用户共享接入和码分多址等三种与卫星相关的NOMA方案叠加。在[173]中，陈等人。利用Polar码解决多载波智能隐蔽卫星通信中低信噪比场景下的同步问题。此外，吴等人。文献[174]中进一步采用了Polar码辅助频偏估计方案来解决频谱限制。基于所提出的方案，他们分析了隐蔽卫星通信的隐蔽中断概率和可实现的传输性能。

隐蔽通信网络解决方案

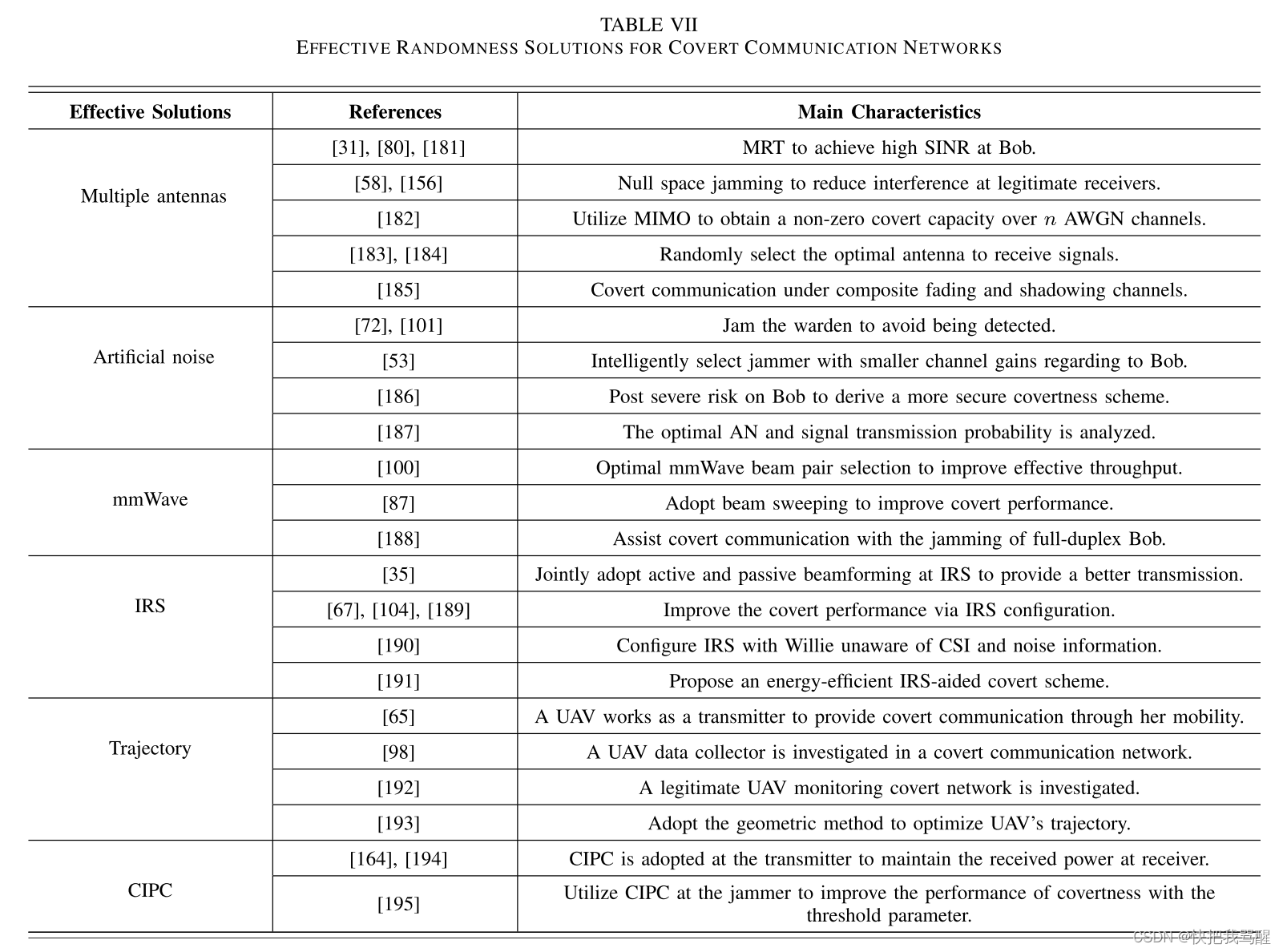
通过引入隐蔽通信可以很好地实现无线安全，特别是对于空对地通信，LoS信道可以使恶意窃听者受益。因此，有必要研究保证隐蔽性的方法。在本节中，我们回顾了几种用于在威利引入不确定性以实现隐蔽性的典型技术，表七总结了这些技术。这些潜在的隐蔽解决方案包括多天线、人工噪声（AN）、毫米波（mmWave）、智能反射面（IRS）、轨迹设计和CIPC，其简要总结如图11所示。

多天线

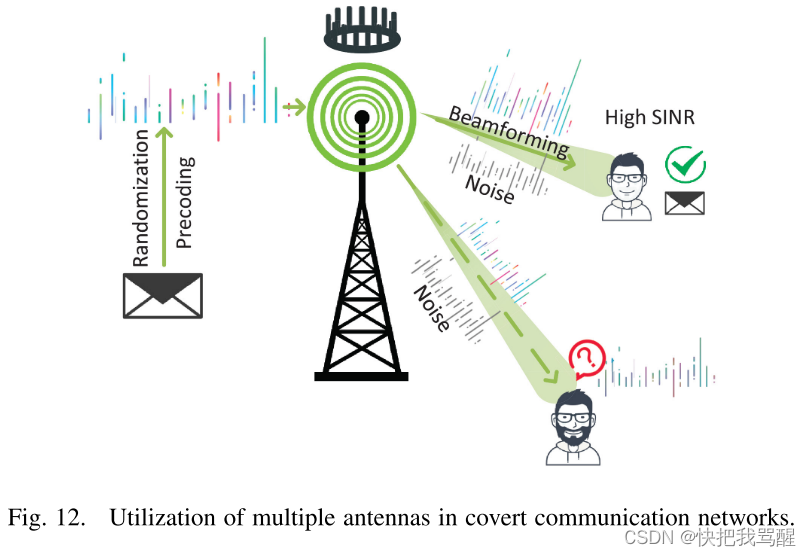
无线通信中多天线的应用可以带来很多好处，包括扩大覆盖范围、增加信道容量、增加用户连接数、提高可靠性等。如图12所示，发射端配备更多天线后，接收到的信噪比可以显着增加[60]，[196]，[197]，[198]。此外，发射机应用 MRT 可以比其他恶意用户更多地提高目标接收机的 SNR。然而，典狱长也可以利用这项技术来降低在 Alice 被发现的风险。

Forouzesh 等人在 Alice 上应用了多个天线。在[80]中，为了帮助提高隐蔽通信网络的性能，其中采用MRT波束成形来提高可实现的速率，同时保持隐蔽性。郑等人也利用了 MRT。在[31]中，比较了CAS和DAS的性能。此外，Forouzesh 等人。在[156]中，Alice采用了多个天线来利用零空间和3D波束成形来提高传输性能。他们在干扰器上使用了多个天线，向典狱长引入干扰，同时将合法接收器置于零空间。在[58]中，Shmuel 等人在干扰机和 Bob 上都配备了多个天线。干扰功率是随机的，它利用波束成形来最大化 Alice 和 Bob 的传输速率。此外，他们还利用Bob处的多个接收天线与干扰器配合，最大化接收SINR。 Bendary 等人利用了多输入多输出 (MIMO)。在[182]中提供了n个AWGN信道上的非零隐蔽容量，它可以满足发射天线快速放大或发射机在Willie上执行零空间的条件。在[181]中，Yu等人。研究了隐蔽通信中多输入单输出（MISO）通道的波束成形。他们证明了复高斯信道下的最优信令是对称复高斯分布。他们还讨论了发射机上不同 CSI 知识的最佳转换。杨等人。在[183]​​和[184]中分别在接收器和中继器处使用了多个天线。在[183]​​中，假设合法的鲍勃选择最好的天线来接收隐藏信息，并利用剩余的天线来干扰威利。结果是在威利知道或不知道他和鲍勃之间的CSI的情况下进行调查的。在[184]中，假设中继站配备了多个天线，并在第一阶段选择其最佳天线来接收来自Alice的信号，同时利用其余天线来干扰Willie。在第二阶段，假设中继利用其多个天线对鲍勃执行迫零以干扰威利。与其他隐蔽通信研究不同，杜等人。研究了[185]中复合衰落和阴影模型下的多天线隐蔽通信。然而，多天线MRT在隐蔽通信中的应用通常需要完善的CSI，这另一方面可能会增加网络的设计复杂度。

人工噪声

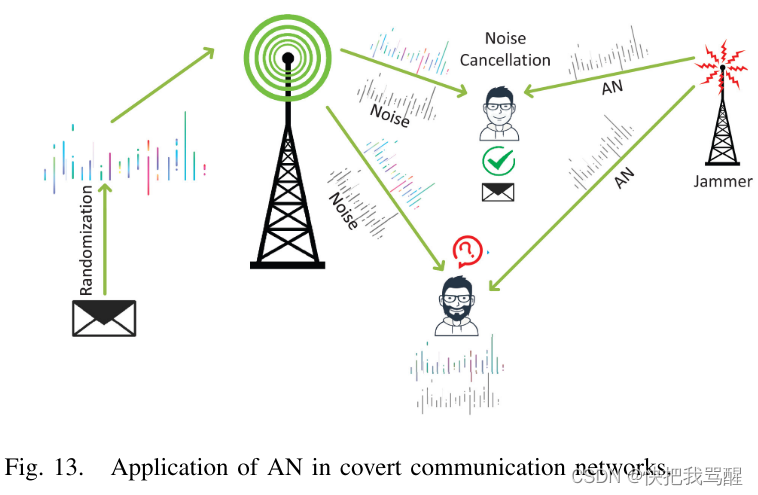
与噪声不确定性、信道不确定性和中继辅助类似，人工噪声可以作为一种有前途的技术来迷惑 Willie 的检测，如图 13 所示。干扰机带来的不确定性可以从随机发射中引入电源，甚至来自具有固定或随机电源的全双工接收器。引入的干扰信号可以与环境噪声和其他不确定因素一起作用，有效地降低典狱长接收到的信号[199]。

黄等人。利用[72]中的友好干扰器通过相互正交的频率接入秘密地向K个用户传输，其中每个用户的干扰序列遵循复杂的高斯分布。在[101]中，Xiong等人。在认知干扰器的帮助下研究了秘密通信。干扰器感知 Alice 在前 m 个时隙中的传输，如果检测到她的传输，就会在其余 m + 1 个时隙中使用复杂的高斯信令进行干扰。结果表明，所提出的认知隐蔽干扰方案可以提高数据传输速率并降低被发现的可能性。与典型的干扰器辅助隐蔽通信不同，Zheng 等人。在[53]中提出了一种方案，可以根据其CSI智能地选择干扰器，以在隐蔽性和吞吐量方面获得更好的性能。为了混淆典狱长的检测并减少鲍勃的干扰，他们选择了与接收器之间信道增益较小的潜在干扰器。由于干扰器的位置和数量带来的不确定性，威利的探测可能会受到严重影响。另一方面，恶意用户也可以利用干扰来破坏合法用户之间的传输。张等人。在[186]中研究了当信道被敌对用户干扰时的隐蔽通信。为了克服这一挑战，他们提出增加共享密钥的大小以保证隐蔽通信的可靠性。在[95]中，赵等人。利用全双工 Bob 来干扰 Willie 的检测。他们研究了通信和窃听链路之间的权衡，其中通过正确选择鲍勃干扰功率的变化范围来优化隐蔽传输。他等人。在[187]中分析并推导了Alice和干扰器的最优传输概率。然而，通过人工干扰引入随机性，干扰信号对合法用户的影响不容忽视，尤其是在无法很好消除的情况下。此外，还应考虑干扰信号的能量效率。

毫米波

毫米波可以利用波束成形来克服严重的路径损耗，并极大地提高隐蔽通信的传输速率。尽管如此，毫米波资源还没有得到很好的利用，这使得毫米波相关通信能够实现更高的传输速率。毫米波具有很强的方向性，可以为隐蔽通信提供固有的安全性，并使威利更难以检测到[50]。

在[100]中，Zhang 等人。首先设计了毫米波隐蔽通信方案，毫米波的方向性有助于保护隐蔽通信的安全。在本文中，Alice 和 Bob 利用波束训练方法在他们之间建立定向链路，并选择最佳波束对进行数据传输。他们还设计了一种方案来联合优化波束训练开销，以最大限度地提高有效吞吐量。此外，张等人。在[87]中通过波束扫描优化了无人机辅助毫米波通信的隐蔽传输速率。利用毫米波的方向性特性，可以更好地保障Alice的传输。他们考虑了在没有鲍勃和威利双方位置信息的情况下进行爱丽丝的传输，并且爱丽丝利用波束扫描来提高隐蔽通信性能。在[188]中，Wang 等人。考虑与全双工 Bob 的隐蔽通信，其中接收器可以发出干扰信号以协助隐蔽通信。他们分析了单数据流和多数据流的场景，性能都可以得到相应的提升。总结一下，高方向性的毫米波一方面可以提供更好的传输性能，另一方面也需要更精准的设计才能达到预期的效果。此外，毫米波容易受到干扰干扰。因此，防止恶意干扰对于基于毫米波的隐蔽通信网络也至关重要。

IRS

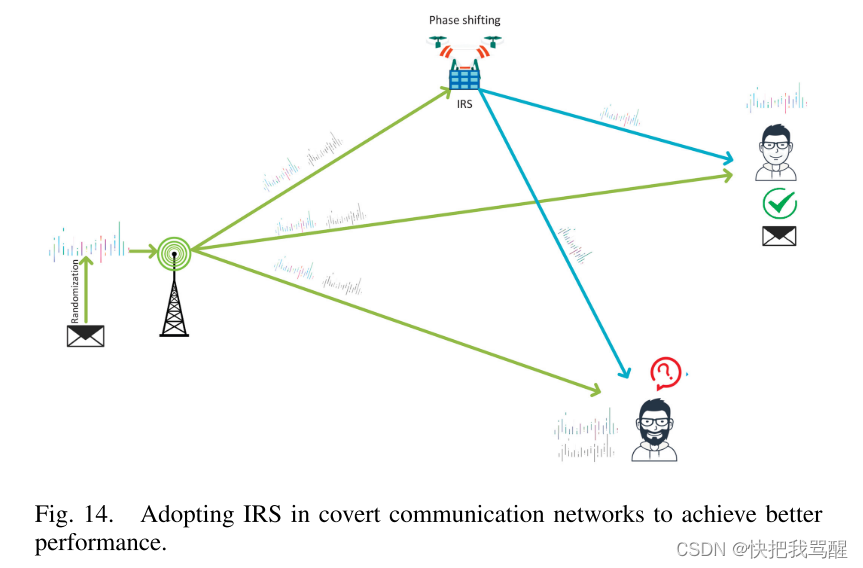
IRS可以通过优化其反射矩阵来设计，以实现目标用户处接收信号的理想方向，如图14所示。与典型的隐蔽通信模型相比，采用IRS可以进一步受益于信道衰落带来的不确定性[77]、[79]、[200]。因此，可以将 IRS 引入隐蔽通信网络，通过重新配置 Alice [83]、[201]、[202]、[203]、[204] 的无线信道来提高合法接收器的隐蔽传输性能。

在[189]中，Lu等人。列出了四种典型的 IRS 增强型隐蔽通信系统，即射频收集、阻塞、干扰和主动攻击。然后，他们进一步分析了如何配置IRS以最大化传输性能同时保持隐蔽性的案例。吴等人。 [67]讨论了当发射器上看守的 CSI 不可用时实用的 IRS 辅助隐蔽场景。他们共同设计了Alice的发射功率和IRS的反射相位以及幅度，以最大限度地减少Bob的中断概率。在[104]中，Zhou等人。研究了 IRS 辅助隐蔽通信的短包方案，其中不确定性是由 Alice 传输的复杂高斯信号引起的。王等人。在[35]中研究了主动和被动波束形成模式下IRS辅助的隐蔽通信。在本文中，Alice 和 Bob 之间的直接链路被阻断，其中采用 IRS 将秘密通信中继到 Bob，它作为全双工干扰器来干扰 Willie 的检测。 Alice 的主动波束成形和 IRS 的被动波束成形联合优化，以提供更好的传输性能，同时在特定约束下保持 Willie 的正确检测概率。在[190]中，Zou等人。在威利研究了关于爱丽丝-IRS 和 IRS-威利之间的 CSI 的不确定性的秘密通信网络，而威利也不知道他的噪声功率。他们分析了实际场景下对威利的检测，实现隐秘通信的隐身性。与大多数现有文献不同，Li 等人。在[191]中研究了一种节能的 IRS 辅助隐蔽通信，其中 IRS 安装在无人机上以提高其覆盖范围。然而，国税局协助的秘密通信存在一些困难。 IRS 的相移矩阵设计高度依赖于估计的 CSI，如果设计不当，可能会导致性能较差。此外，IRS的引入也会导致更高的路径损耗。因此，应仔细考虑通道设计和信号衰减之间的权衡。

轨迹设计

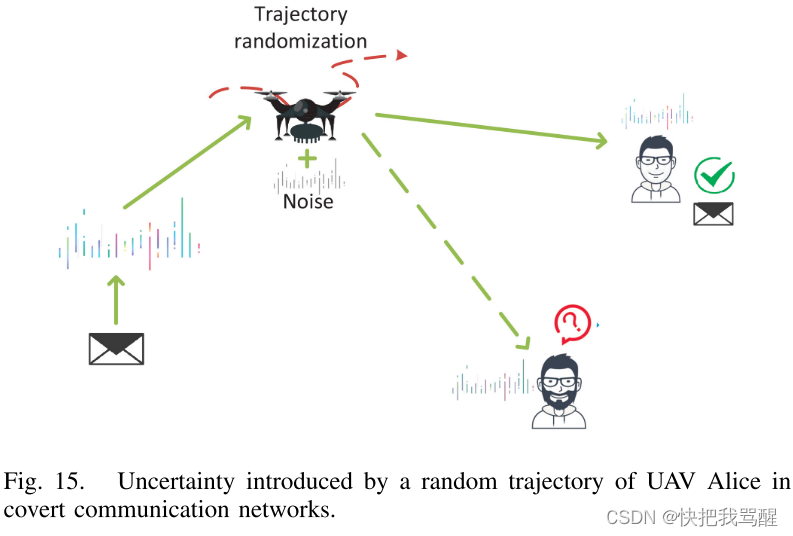
无人机因其机动性高、配置方便、信道条件优越等优点引起了学术界的广泛关注。无人机通信引入不确定性的最典型技术之一是利用随机信道衰落。进一步将无人机的移动性与信道衰落相结合，可以大大改善在warden处引入的不确定性，如图15所示，这有助于大大提高Alice的隐蔽性。

在[65]中，Jiang等人。讨论了无人机在隐蔽通信中的应用，详细讨论了无人机的功能类别。然后，他们提出了一种有效的方案，其中无人机作为发射器，利用其移动性秘密向多个地面用户传输，同时最大化数据容量。周等人。在[98]中考虑了来自地面用户的上行链路隐蔽传输，其中给管理员带来的不确定性是由信道衰落引起的。具体来说，对无人机的轨迹进行了优化，以在保持隐蔽性的同时实现更高的数据速率。在[192]中，胡等人。考虑了隐蔽通信中的合法无人机监控。他们优化了推进力和推力以及轨迹，以实现更好的监控性能。拉奥等人。在[193]中利用几何方法来优化无人机隐蔽网络的轨迹。因此，位置随机性是一个有趣的设计，尤其是在无人机相关的隐蔽通信网络中。然而，设计假设应该是实用的，因为无人机的速度是有限的，这限制了其位置变化范围。

CIPC( channel inversion power control )

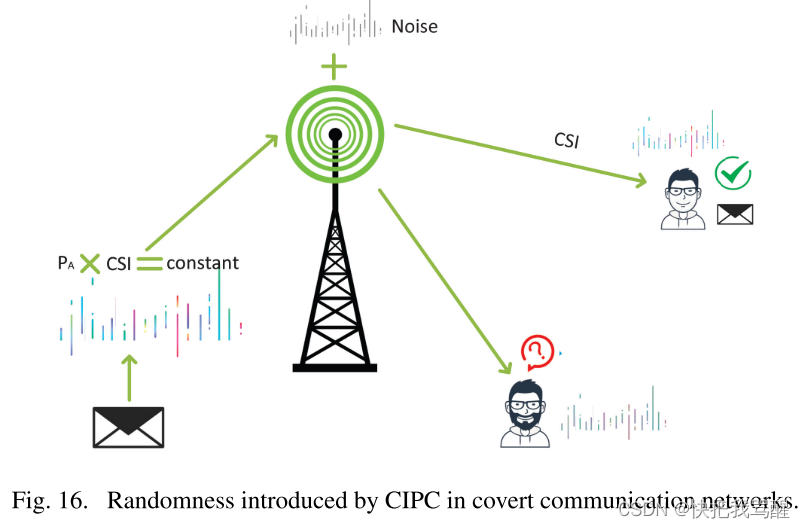
CIPC 指示发射机改变其发射功率，以将信号的接收功率维持在其目标用户处的特定常数。通过利用 CIPC，Bob 处的接收信号功率可以设计为保持恒定，但 Willie 处的接收功率将根据信道衰落而变化。这可以用来给 Willie 引入额外的不确定性，同时保持合法用户的传输性能，如图 16 所示。

在[194]中，胡等人。利用发射机处的瑞利衰落进入 CIPC 来实现有保证的通信性能，同时给管理员带来不确定性。 Alice根据她和Bob之间的信道系数反向随机化她的发射功率，以混淆Willie的检测。另外，接收器发射随机功率的全双工干扰信号，这使得Alice能够以更高的发射功率保证安全。根据时间不容忍系统，Ma 等人。在[164]中研究了CIPC辅助的隐蔽通信。除了CIPC瑞利衰落的影响外，Alice还采用高斯信令在Willie处引入不确定性。推导了 Willie 的最佳检测阈值，并证明了最大有效隐蔽吞吐量。在[195]、[205]中，Wang等人。研究了与 CIPC 干扰器的秘密通信，该干扰器利用 CIPC 来避开信道估计导频，并给 Warden 的检测带来不确定性。他们证明了通过CIPC预设的阈值参数可以提高隐蔽性的性能。哈兹-维尔科夫等人。利用 CIPC 在[206]中提出了一种近乎理想的 NOMA 网络隐蔽方案。然而，CIPC 最关键的要求是信道估计。如果没有可靠的 CSI 估计，发射机的功率控制将难以实现。

新兴应用和场景

随着无线技术的快速发展，隐蔽通信需要进一步改进方法，以引入不确定性并适应新兴应用和场景的安全要求，特别是应对管理员日益增长的计算能力。在本节中，我们讨论和阐述隐蔽通信的潜在应用和可能的场景，其简要摘要如图 17 所示。

6G

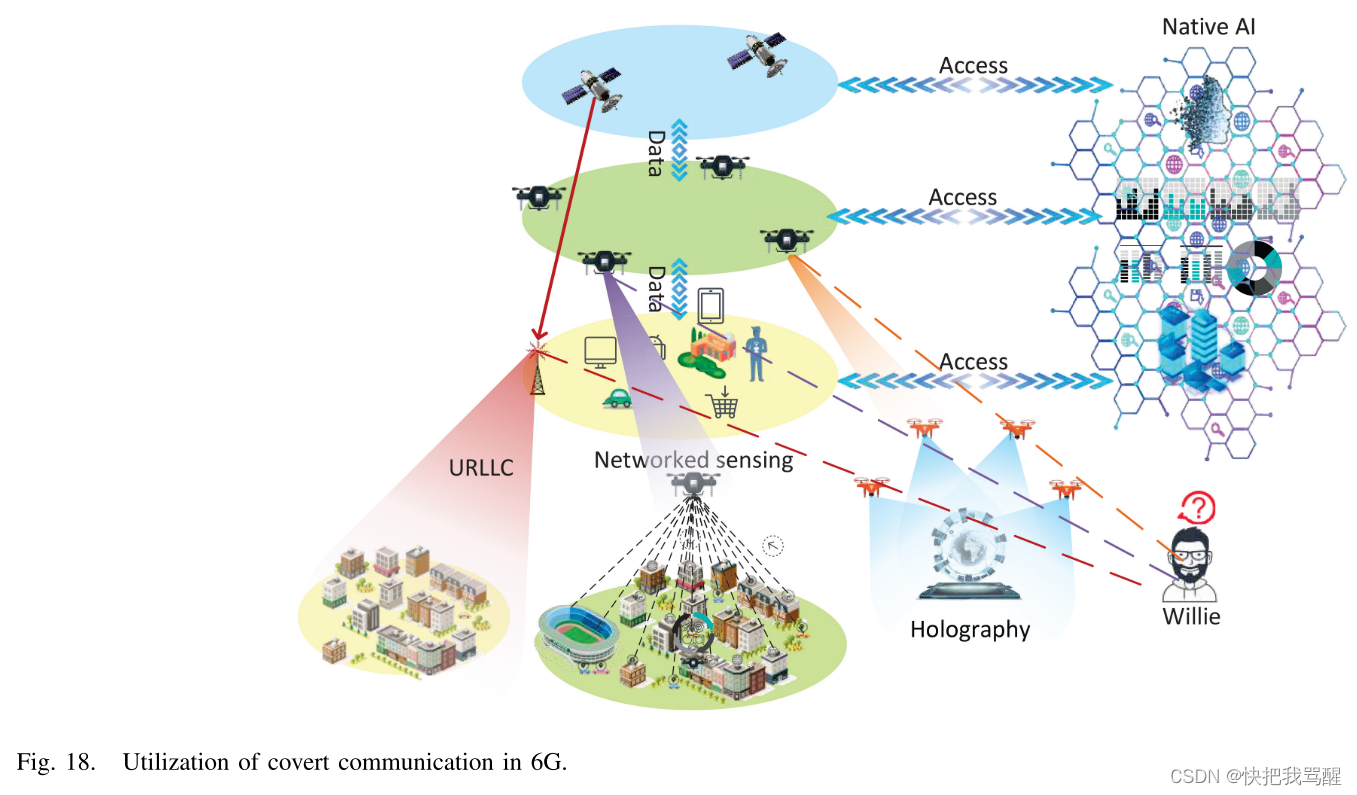
移动设备使每个人都可以随时随地与任何人一起访问互联网。具体来说，无线通信的便利性让人们想象互联网变得更快、更容易访问、甚至更加多样化。 6G的动机是提供更高的传输速率、更少的时延和更全面的无线覆盖[207]、[208]。它提出了天地海无缝覆盖的概念，人类社会的信息将在任何地方都可用，因此安全性变得更加关键[209]。此外，6G无处不在的连接需要更加复杂的通信协议，其复杂度极高，保障传输安全面临巨大挑战。通过利用隐蔽通信，可以进一步保证用户安全，基本场景如图18所示。In[94]，Ma等人。研究了主动和被动模式的 6G 无线通信混合设备的隐蔽通信。他们探索了有源链路固有的不确定性，借助充当干扰源的无源反向散射传感器来实现隐蔽性。然而，6G相关的隐蔽通信仍需要进一步研究。利用无处不在的设备和新技术实现隐蔽通信，是今后的重点。

THz

太赫兹（THz）被定义为频率范围从0.3 THz到3 THz的电磁波，它通过探索更多可用的频率资源极大地拓宽了无线通信的频带[210]。由于其方向特性和较窄的波束，太赫兹被认为比传统的低频通信更安全。尽管太赫兹作为一种高频通信，存在由扩频和散射引起的严重信道衰落的缺点，但它可以避免波束扇区外的检测[211]。与太赫兹相关的研究已经有一些，但太赫兹的信道模型仍未得到充分研究。在[212]中，Gao 等人。提出了一种距离自适应吸收峰值调制隐蔽通信方案，以利用频率相关的分子吸收。他们首先制定了基本的太赫兹隐蔽通信指标，然后分析了所提出方案的隐蔽性能。然而，高度方向性的特性也对Alice和Bob之间的传输造成了很大的威胁，一旦恶意用户阻断了直接的LoS链路，就很容易被阻断。刘等人。在[107]中提出利用非视距（NLoS）将固定传输路径迁移到不可预测的路径，以隐藏信息传输并避免被终止。他们建议利用镜面反射分量来散射隐蔽信号。然而，现有的太赫兹相关隐蔽通信研究仍然有限，许多基本概念尚未明确。例如，太赫兹通信的基本信道模型和传输特性仍然需要开发。此外，仍需要开发在威利引入更多不确定性的技术。

Integrated Sensing and Communication (通感一体)

随着无线设备需求的发展，频率资源变得越来越稀缺。结合传感和通信目前可以共享重叠的频段，这可能会导致对这两个系统的干扰[213]。然而，通过共享无线电资源和硬件平台，可以消除干扰并进一步提高性能，这被称为集成传感与通信系统[214]、[215]。集成传感和通信的一种可能的隐蔽场景是，Alice在向Bob传输过程中尝试通过传感信号来检测Willie的位置，然后，Alice在获得Willie的位置信息后可以对Willie引入更多的定向干扰。因此，隐蔽的联合传感通信系统可以更有效地解决活跃或移动的威利[216]。通过雷达检测​​，Alice 可以检测 Willie 并估计 CSI，这为向典狱长进行零迫波束形成提供了更多信息。然而，隐蔽联合传感通信系统需要解决的关键问题之一仍然是如何发送嵌入安全信息的探测波形而不被管理员检测到。在[217]中，杜等人。将隐蔽通信应用于联合雷达通信系统，以实现更好的频谱利用和信息安全。

空间信息网络（Space Information Networks）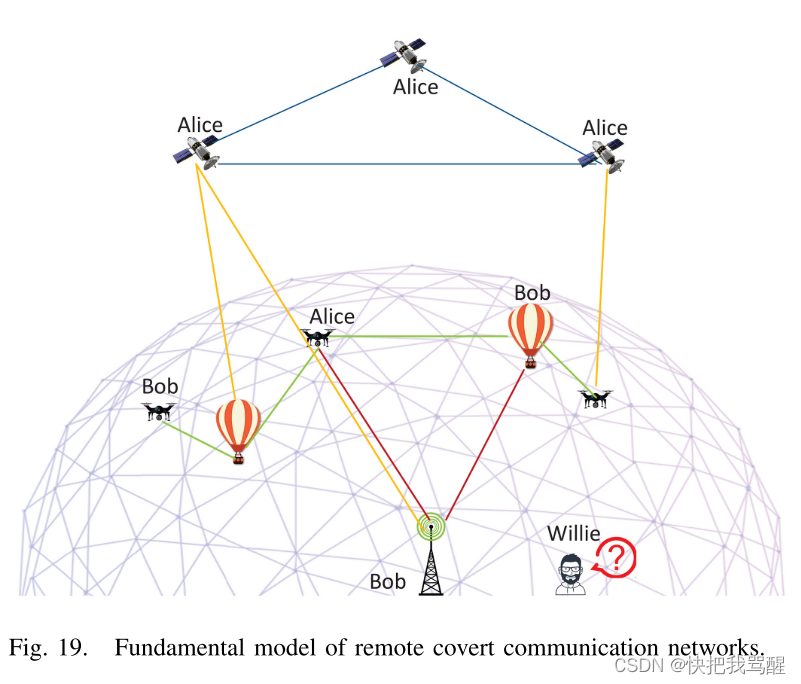

空间信息网络是指航天器与地面基站之间的数据传输，可利用不同类型和功能的卫星、平流层气球、无人机等设备，结合星间链路和星空地链路，提供空间全覆盖。综合天地信息系统[218]。与传统地面无线网络相比，空间信息网络具有全覆盖、快速配置、受环境限制少等优势。但超长距离会造成严重的时延，可以通过短包传输来解决。尽管如此，空间信息网络仍然存在一些安全挑战，可以借助隐蔽通信[219]来解决，如图19所示。将隐蔽通信植入空间信息网络的关键任务是防止在保证高传输速率、无缝覆盖、低时延。安全信号可以通过带有时隙选择的隐蔽通信来传输，这限制了平均传输速率。此外，还降低了发射功率，以降低在隐蔽通信网络中被检测到的风险。因此，需要开发更强大的不确定性引入方法，在提高空间信息网络传输性能的同时保证隐蔽性。

未来的问题和公开的挑战

通过上述方案，可以保证通信的隐蔽性，且被看守者发现的概率较低。然而，为了提高隐蔽性能，仍然存在一些需要克服的挑战。表八总结了秘密通信的主要挑战和潜在解决方案。

1 Active Willie

与Willie处于固定位置或进行被动检测的典型场景不同，主动Willie可以称为移动典狱长或主动攻击典狱长。

对于移动威利来说，这表明威利可以根据接收到的信号动态改变他的检测位置和功率阈值[93]。威利可能距离爱丽丝很远，并且可以测量他接收到的信号来分析爱丽丝是否正在发送信号。如果他发现Alice有一些可疑的行为，他可以靠近并进行进一步的检测和分析。重复几次这个接近和检测的过程后，他可以更精确地判断Alice是否正在传输。

至于主动攻击，则意味着威利不再满足于被动检测，当他发现爱丽丝的传输时，可能会产生干扰。当威利判定爱丽丝正在传输后，他可以发送人工噪声来干扰爱丽丝的传输并影响鲍勃的接收。**当威利距离鲍勃比爱丽丝更近时，这可能会更令人沮丧，因为威利可以用相当低的功率干扰鲍勃，并且具有更好的干扰效果。**然而，目前与隐蔽通信相关的研究很少考虑主动威利，可以进一步探索这一点，为隐蔽传输提供更彻底的保护。

2 Utilization of MIMO

通过采用MIMO，可以利用无线信道的优势显着提高接收信号的总功率。此外，MIMO 还可以利用预编码来最大化目标接收器处的 SINR，同时将非法接收器置于零空间中。然而，大多数有关隐蔽通信的多天线研究仅涉及多输入单输出（MISO）情况。在未来的隐蔽通信方向中，还应该考虑威利或鲍勃的多个天线，这仍然是一个严峻的挑战。对于多天线Willie，接收信号功率分布需要进一步讨论，需要提供更多的概率分布分析。对于多天线Bob，需要研究他的解码向量的设计。尽管MIMO解码向量的设计在5G网络中已经得到了很好的研究，但对于引入不确定性的隐蔽无线网络，仍需要进一步考虑。因此，未来与MIMO隐蔽通信相关的工作应该包括如何为Bob设计解码向量以及对多天线Willie的分析。

3 Powerful Willie

当前的分析通常假设威利将其功率检测阈值设置为最佳值并保持固定。当威利可以利用机器学习，或者调整阈值以进行更精确的检测时，这种情况会变得更糟。机器学习可以帮助威利降低错误检测的概率，这将对爱丽丝构成很大的威胁。目前，机器学习仍面临训练开销高、稳定性差、适应性困难、样本有限等问题。对于合法的监视，合法典狱长Warden可以利用机器学习来更精确地估计 CSI，以帮助检测。通过被动检测，合法典狱长无法获取自己与非法Alice之间的CSI。因此，如果他能够采用机器学习来检测，他的检测将会更加准确。

4 Imperfect CSI

薄弱的 Alice 也会导致隐蔽通信性能不佳。以前的工作通常假设 Alice、干扰者或合法中继者完全了解合法用户中的 CSI。他们假设可以通过发送导频来获得实时CSI，这有些不切实际。福鲁泽什等人。在[81]中研究了发射机无法获得完美CSI的情况，他们讨论了三种情况：1）在特定范围内可以获得信道分布信息（Channel Distribution Information, CDI），2）获得CDI的均值和方差，3 ) **方差对于发射机来说是未知的。**参考[81]，可以进行更多与弱Alice相关的研究，为无线传输提供更彻底的隐蔽性保护。此外，合法的监视管理员也希望在自己和非法发送器之间有一个更完美的CSI估计[85]。

5 毫米波中的泄漏和阻塞(Leakage and Blockage in mmWave)

毫米波因其波长短、方向性强的特点而成为无线通信的关键技术。尽管毫米波吸收性强，在非视距信道下无法提供令人满意的性能，但由于其波长短，它仍然在个人区域无线网络中得到广泛应用。高度定向的波束使得毫米波能够直接准确地传输到所需的接收器，而不会散射到其他用户，从而保证了传输的安全性。尽管如此，信息泄露问题仍然存在，这可能会在威利发现的情况下 post 爱丽丝的传输。此外，Alice 和 Bob 之间的毫米波传输可能会在 NLoS 链路中被阻止。未来的研究可以进一步考虑利用IRS或其他技术来解决毫米波的这一固有问题。

6 Uncertainty Techniques

Alice之所以能够向Bob传输信号而不被Willie检测到，是因为她可以将自己的信号隐藏在环境或人工噪声中以避免Willie检测到。然而，隐藏探测模式是爱丽丝和威利之间的竞争游戏，威利在争取更精确的探测，而爱丽丝则竭尽全力让自己的信号在威利面前消失。除了环境噪声之外，隐蔽通信中使用的典型解决方案包括：1）小规模信道衰落的不确定性，2）发射功率随机化，3）位置变化，以及4）干扰功率随机化。上述不确定性解可以单独使用，也可以组合使用。在[220]中，Wang等人。提出了一种概率累积然后传输方案，其中Alice可以调整能量收集和信息传输的先验来迷惑Willie的检测，从而实现隐蔽性。然而，隐蔽通信网络在未来仍然需要更有效的技术来带来不确定性并提供更坚实的隐蔽性。

CONCLUSION

这项调查对隐蔽通信进行了广泛的审查，这是一种关键的安全技术，可以通过隐藏传输的存在来提供全面的安全保护。首先，我们解释了隐蔽性理论的基本知识，并比较了其与其他安全方法的区别。然后，详细介绍并比较了隐蔽传播研究的不同分支。概述了不同网络中隐蔽通信的各种应用。特别是，总结和解释了在秘密通信中用来隐藏隐形信号以防止监视者发现的技术。此外，还分析和讨论了隐蔽通信的新兴应用和潜在场景。最后，我们讨论了隐蔽通信未来可能出现的问题，并展示了潜在的研究方向。

---

---

---

一、Limits of Reliable Communication with Low Probability of Detection on AWGN Channels

2013年JSAC的论文

摘要

我们针对可以在加性高斯白噪声（AWGN）信道上低概率检测（LPD）并可靠地传输的信息量，提出了一个平方根的限制。具体地说，如果发射机具有AWGN信道到预期的接收机和warden，两者都具有非零噪声功率，我们证明了$O(\sqrt{n})$个比特可以在n个信道使用中从发射机发送到接收机，而对于任何$ϵ>0$，下限$\alpha +\beta \ge 1-ϵ$，其中$\alpha$和$\beta$分别表示warden当发送方不发送时的虚警概率和当发送方发送时的漏检概率。此外，在大多数实际场景中，发射机和管理员之间的信道上的噪声功率的下限是已知的，并且可以在$n$个LPD信道使用中发送$O(\sqrt{n})$位。相反地，尝试传输多于$O(\sqrt{n})$个比特要么导致warden以概率1检测到，要么导致接收器处的解码错误的非零概率为$n\to \inf$。

introduction

在无线链路上传输安全信息是消费者、工业和军事应用的首要关注。通常，使用各种加密和密钥交换协议来保护在无线网络中传输的数据不被窃听者拦截。然而，有许多现实生活中的场景，其中标准的加密安全性是不够的。加密的数据会引起怀疑，即使是理论上最强大的加密也经常会被使用非计算方法（如侧信道分析）的坚定对手击败。这样的场景需要低检测概率（LPD）通信，这首先阻止了对传输的检测。

虽然实际的LPD通信已经在扩频社区中被充分研究[1，Pt.5，第1章]，信息理论的极限还没有被探索。因此，我们开发的LPD通信在加性高斯白噪声（AWGN）无线信道上的基本界限。在我们的场景中，Alice通过AWGN信道与Bob通信，而被动窃听者Warden Willie试图检测她的传输。Alice和Willie之间的信道也是AWGN，并且Willie是被动的，因为他不主动干扰Alice的信道。Alice向Bob发送低功率信号，Willie试图将其分类为来自Alice的信道上的噪声或Alice向Bob发送的信号。如果他检测到通信，威利可能会关闭信道或以其他方式惩罚爱丽丝。如果威利和爱丽丝之间的信道上的噪声具有非零功率，则Alice可以在容忍一定的检测概率的同时与BoB通信，她可以通过以足够低的功率发送来降低检测概率。因此，Alice潜在地在信道的$n$次使用中跨LPD信道向Bob发送非零互信息。

我们的问题与imperfect steganography有关，它考虑通过改变固定大小、有限字母隐藏文本对象（例如图像或软件二进制代码）的属性来隐藏信息，同时容忍管理员检测到隐藏信息的固定概率。被动典狱长环境中隐写术的平方根定律规定，可以安全地修改大小为 n 的隐藏文本中的 O(√n) 个符号，以隐藏 O(√n log n) 位隐写术消息 [2，第 1 章]。 13]，其中 log n 因子直接源于这样一个事实：向 Bob 的传输是无噪声的 [2，Ch. 13]。 8]。在我们的场景中，爱丽丝使用她与威利的频道上的噪音而不是隐藏文本的统计属性来隐藏信息。然而，必须针对她发送给 Bob 的通道上的噪声进行编码，在 LPD 通道的 n 次使用中只能发送 O(√n) 位。1 统计假设检验的数学在这两个问题中都得出了平方根定律，但如下所示：由于沟通渠道的根本差异，对不同问题的回答也不同。这种关系将在第三节末尾进一步讨论。

Our problem is related to imperfect steganography, which considers hiding information by altering the properties of fixed-size, finite-alphabet covertext objects (such as images or software binary code) while tolerating some fixed probability of detection of hidden information by the warden. The square root law of steganography in the passive warden environment states that $\mathcal{O}(\sqrt{n})$ symbols in covertext of size $n$ may safely be modified to hide an $\mathcal{O}(\sqrt{n}\log n)$ -bit steganographic message [2, Ch. 13], where the $\log n$ factor stems directly from the fact that transmission to Bob is noiseless [2, Ch. 8]. In our scenario, Alice uses the noise on her channel to Willie instead of the statistical properties of the covertext to hide information. However, having to code against the noise on her channel to Bob allows only $\mathcal{O}(\sqrt{n})$ bits to be sent in $n$ uses of the LPD channel. ${}^1$ The mathematics of statistical hypothesis testing yields a square root law in both problems, but as answers to different questions due to the fundamental differences in the communication channels. This relationship is discussed further at the end of Section III.

We state our main result that limits the amount of information that can be transmitted on the LPD channel between Alice and Bob using asymptotic notation [3, Ch. 3.1] where $f(n)=\mathcal{O}(g(n))$ denotes an asymptotically tight upper bound on $f(n)$ (i.e. there exist constants $m,n_0>0$ such that $0\le f(n)\le mg(n)$ for all $n\ge n_0)$, $f(n)=o(g(n))$ denotes an upper bound on $f(n)$ that is not asymptotically tight (i.e. for any constant $m>0$ , there exists constant $n_0>0$ such that $0\le f(n)<mg(n)$ for all $n\ge n_0)$ , and $f(n)=\omega (g(n))$ denotes a lower bound on $f(n)$ that is not asymptotically tight (i.e. for any constant $m>0$ , there exists constant $n_0>0$ such that $0\le mg(n)<f(n)$ for all $n\ge n_0)$ :

Theorem (Square root law). Suppose the channels between Alice and each of Bob and Willie experience additive white Gaussian noise (AWGN) with powers ${\sigma }_b^2>0$ and ${\sigma }_w^2>0$ , respectively, where ${\sigma }_b^2$ and ${\sigma }_w^2$ are constants. Denote by $\alpha$ the probability that Willie raises a false alarm when Alice is not transmitting, and by $\beta$ the probability that Willie does not detect a transmission by Alice. Then, provided that Alice and Bob have a shared secret of sufficient length, for any $ϵ>0$ and unknown ${\sigma }_w^2$ , Alice can reliably (i.e. with arbitrary low probability of decoding error) transmit $o(\sqrt{n})$ information bits to Bob in $n$ channel uses while lower-bounding Willie’s sum of the probabilities of detection errors $\alpha +\beta \ge 1-ϵ$ . Moreover, if Alice knows a lower bound ${\hat{\sigma }}_w^2>0$ to the power of the AWGN on Willie’s channel ${\sigma }_w^2$ (i.e. ${\sigma }_w^2\ge {\hat{\sigma }}_w^2$ ), she can transmit $\mathcal{O}(\sqrt{n})$ bits in $n$ channel uses while maintaining the lower bound $\alpha +\beta \ge 1-ϵ$ . Conversely, if Alice attempts to transmit $\omega (\sqrt{n})$ bits in n channel uses, then, as $n\to \infty$ , either Willie detects her with arbitrarily low probability of error or Bob cannot decode her message reliably, regardless of the length of the shared secret.

On Covert Communication With Noise Uncertainty

CL 2017年的论文。

摘要

先前关于噪声不确定性的covert 通信的研究从warden的角度采用了最坏情况的方法。即用warden最坏情况下的检测性能来评估隐蔽性，这过于乐观了。我们不是简单地考虑最差限制，而是考虑噪声不确定性的分布，以从统计意义上评估整体隐蔽性。具体来说，我们定义了用于测量隐蔽性的新度量，然后采用这些度量来分析有界和无界噪声不确定性模型下给定隐蔽性要求的最大可实现速率。

metrics: Covert Rate 隐蔽速率

现在，我们研究在平均隐蔽概率（即隐蔽率）的约束下，Alice 能够与 Bob 可靠通信的最大速率。将隐蔽速率表示为 $R$，问题可表述为:

$$\begin{array}{l}{\max }_{P_t}R=\frac{1}{2}{\log }_2\left(1+\frac{P_t}{r_b^{\alpha }{\sigma }_b^2}\right)\\ \text{ s.t. }\bar{\xi }\ge 1-ϵ.\end{array}\text{\hspace{1em}(9)}$$

正如备注 1 中所解释的，在本工作中， (错误概率)$\bar{\xi }\ge 1-a$ 的要求相当于 $p_{out}\le a$ 的要求。因此，本节我们不考虑 $p_{out}\le a$ 的要求。

然后这篇文章就分成了约束的不确定性模型，无约束的不确定性模型，然后文章就推出了模型下的隐蔽速率的具体表达式，而隐蔽速率中其中关键的一项是推导Willie处的接收功率判定阈值：
the received power threshold at Willie below which $\bar{\xi }\ge 1-ϵ$ is given by。
$$P_{\mathrm{LU}}=\left({\rho }^{2ϵ-1}-\frac{1}{\rho }\right){\sigma }_n^2\text{\hspace{1em}(10)}$$
类似这种

---

---

---

Intelligent Reflecting Surface Assisted Covert Communication With Transmission Probability Optimization

大部分是需要这样算概率密度函数:

$${\mathbb{P}}_{\mathrm{MD}}(\gamma ,\eta )={\int }_0^{\gamma -P_{\mathrm{A}}\eta }{f}_{{\sigma }_{\mathrm{W}}^2}(x)\mathrm{d}x$$
算期望，具体要怎么推呢。

---

---

---

Fundamental Limits of Covert Communication over MIMO AWGN Channel

已经针对不同的标量通道模型研究了隐蔽通信的基本限制。结果表明，通过 $n$ 个独立的信道使用，$O(\sqrt{n})$ bits可以通过公共信道可靠地传输，同时实现其他站的任意低检测概率 (LPD)。这个结果被称为平方根定律，甚至为了实现这种递减的秘密通信率，所有现有的研究都利用了发送器和接收器之间共享的某种形式的秘密。在本文中，我们确定了 MIMO AWGN 信道上 LPD 通信的限制。特别是，使用相对熵作为我们的 LPD 度量，我们研究了发射机可以保证可靠性和满足 LPD 条件的最大码本大小。我们首先证明，在 δ-PD 约束下生成输入分布的最优码本是零均值高斯分布。然后，假设仅在发射机的主信道上存在信道状态信息（CSI），我们推导最佳输入协方差矩阵，从而建立码块大小的缩放法则。我们评估了信道使用数量（渐近块长度）和天线数量（大规模 MIMO）限制条件下的码本缩放率。我们证明，在渐近块长度机制中，平方根定律对于 MIMO AWGN 仍然成立。同时，在大规模 MIMO 限制下，码本大小虽然与 $\sqrt{n}$ 线性缩放，但随着发射天线的数量呈指数缩放。我们的结果的实际意义是，MIMO 有可能大幅增加(可以在相当低的延迟下秘密地进行通信的)文件大小。

Key words：LPD communication, Covert MIMO Communication, MIMO physical layer security, LPD Capacity.

Intro

我们的一些发现可以总结如下。对于一个各向同性的Willie信道，我们表明，爱丽丝可以发送$O(N\sqrt{n/M})$bits可靠地在$n$个独立的信道使用，其中$N$和$M$是鲍勃和威利信道的活动本征模的数量，分别。此外，我们评估δ-PD速率在信道使用的数量（渐近块长度）和天线数量（大规模MIMO）的限制制度。我们表明，虽然平方根定律仍然适用于MIMO AWGN，可以秘密发送的比特数与发射天线的数量成指数比例。我们的研究结果的实际意义是，MIMO有可能提供一个可以隐蔽地进行通信的文件大小的大幅增加，在合理的低延迟下。

模型