dfs与bfs的简单总结及应用 | 详解_bfs dfs

本来想昨晚总结一下的，但是不小心玩起了游戏 ，当作放松一下了，现在我们进入正题：

一、$dfs$的简要说明

(1)：深度优先搜索（Depth-First-Search）是搜索算法的一种。是沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节$v$的所有边都己被探寻过，搜索将回溯到发现节点$v$的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。属于盲目搜索。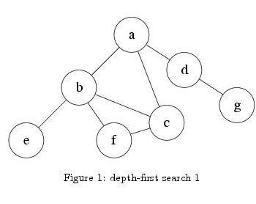

(2)：$DFS$是图论里面的一种搜索算法，他可以由一个根节点出发，遍历所有的子节点，进而把图中所有的可以构成树的集合都搜索一遍，达到全局搜索的目的。所以很多问题都可以用dfs来遍历每一种情况，从而得出最优解，但由于时间复杂度太高，我们也叫做暴力搜索。

(3)：$DFS$如同数据结构中的栈结构，是属于一种后进先出的结构，比如说一个羽毛球筒，把它装满之后，我们开始使用时，拿的总是最后放进去的那一个。所以这就导致了所有的点进入栈时有一个顺序，我们称之为 ：DFS序。

(4)：根据dfs的英文全写，我们可以知道这是一种深度优先搜索的搜索算法，什么叫做深度优先？意思就是它搜索一颗子树时，它要遍历到底才会 “回头” ，比如说：上有向图中的 搜索模式 为(以DFS序来描述)：$a->b->e->b->f->c->f->b->c->b->a->c->a->d->g->d->a$，有人就会问为什么搜索到$c$的时候不搜索$a$呢？因为我们假设的这是一个有向图。而且我们可以看到如果 你面对的图是一个 无向图，这个时候这个树将会持续搜索因为可能会形成环路，使得栈的结构一直进进出出，导致程序崩溃，所以我们也因该注意，在写DFS时，如果面对的是一个无向图的话我们需要进行标记。
一般的标记方法有:

1. ①这个点的父节点被标记，使得子节点不能回到父节点造成循环
2. ②访问过的节点被标记。

这两种方法视情况而定。

(5)：对于暴搜来说，因其复杂度太高，就会想去优化它的复杂度，这一过程称为剪枝，剪纸分为可行性剪枝和最优化剪枝，关于剪枝引申出一种名为记忆化搜索的方法，该方法与动态规划类似。

二、$BFS$的简要说明

(1)：与$DFS$相对的那就是$BFS$了，$BFS$称为宽度优先搜索也叫做广度优先搜索，他是按层遍历每一种状态的下一种状态。
搞不懂？没关系我们来看一下一个例题：
给你一个整数$X$，问是否存在一个这样一个数字$A$：

1. ①这个数字是X的倍数
2. ②这个数字仅由0与1这两种数字组成 例如 X=2，A=10。

这个题当然可以用 $DFS$来做，我们以$1$为起点 这样就成了一个$01$ 二叉树，意思就是说每一种 情况 我们都可以 有两种选择 要么 添0，要么在后面 添1。所以我们可以写出代码：

void dfs(int start)
{
    if(A%X==0)//这是我们搜索结束的条件
    {
        ans=A;//让ans记录答案开始return
        return;
    }
    dfs(start*10);
    dfs(start*10+1);
}
1
2
3
4
5
6
7
8
9
10

这样我们就完成了搜索，起始量为1 搜先 1会变成10，11，然后10会变成100和101，11变成110与111。我们这就完成了所有的情况遍历，当A%X==0时我们记录最后的答案。

所以我们开始试例子：输入 $2$按照$dfs$序，首先不符合条件，然后进入下一步搜索，$X\ast 10=10$，发现$10\%2==0$，然后开始返回ans记录A，这就是最后答案，但是你会发现程序崩溃了。

我们分析一下原因：

$DFS$为深度优先搜索，所以我们的左子树可以看作是在末尾加$0$，然后右子树可以看作在末尾加$1$，所以这样就形成了一棵树。按照$DFS$我们的意图是让他搜索左子树，所以在左子树中找到了 满足条件的 数 ：$10$。但是为什么程序会崩溃呢？
因为搜索到树之后，按照我们刚刚的$DFS$序，这个树遍开始回溯(你可以想象成这棵树开始回缩)，每回溯到一个节点，因为这个节点的 右子树还没有搜索，所以会再去搜索这个节点的右子树，但是这个节点的右子树是在末尾进行加1，而末尾是$1$绝对不可能是$2$ 的倍数 所以这个树会一直按照 往右子树 搜索的趋势 进行下去，导致程序崩溃。

(2)：那是不是这个问题只能枚举了呢？其实$DFS$是可以的，当搜索的深度为$19$时，因为此时的数字位数已经到达了1<<19，此时的答案一定会出现，这时候回溯就好了。所以说我们加一个step记录深度就可以了：

void dfs(int start,int step)
{
    if(A%X==0&&step==19)//这是我们搜索结束的条件
    {
        ans=A;//让ans记录答案开始return
        return;
    }
    dfs(start*10,step+1);
    dfs(start*10+1,step+1);
}
1
2
3
4
5
6
7
8
9
10

(3)：还有没有更好的方法呢？在考虑这个问题的时候我们回顾一下刚刚为什么程序崩溃，原因就是因为DFS是一个深度优先搜索，他每次必须要 深搜到底 ，所以对于末尾是1来说永远没有结束条件所以它一直会搜索下去！这个时候我们可不可以想有没有这样一种搜索模式，出现A=10这个情况之后我们立刻停止就可以了呢？当然是有的，那就是BFS。

(4)：弄完上面这个例题，也就真正的引出了$BFS$也发现了$DFS$的一些小缺点。下面说一下上面留下的定义：按层遍历每一种的状态的下一种状态。首先$BFS$是与数据结构中的 队列 相似，队列是一种 先进先出的结构，这又比如说 你把一些水果按时间一天一个放进一个箱子里，但这些水果时间长了会变质，我们假设变质日期是一样的，那么你每次拿都是拿的最早放进去的那个。
我们来看一下它的搜索模式：
BFS的访问过程与图中序号一致

如果我们按照$BFS$顺序搜索，就会时上图的样子，首先把 根节点 1放进去，然后把他的$3$个子节点放入队列之中，然后第一个再把第一个进入队列的子节点的三个子节点放入对列中，然后再去访问第二个放入队列的也就是上图中的3号点，所以我们看到这个过程 是一层层的搜索，把这一层所有的情况搜索一遍，又把这一层所有状态对应的下一种状态入队列，这样一步步 搜索完成。
(4)：所以说对于刚刚那个题目而言，我们如果按层遍历就不会出现程序崩溃的现象，比如说 第二层有$10$ $11$，那我们就不必搜索下一层了。因为这一层里面已经有我们想要的答案了。具体伪代码：

 1入队列
 	取出当前队列的首元素，用一个值记录，然后扔掉。
 	符合要求？跳出循环：继续状态搜索
 	把该元素对应的 两种状态入队列 （+0，+1）
1
2
3
4

在这里打个广告吧，介绍一下我的公众号， 刚开始做，对于对算法感兴趣的同学或者正在找工作学习的同学非常有帮助喔，会不定期更新大厂笔试内容、计算机基础知识，同时也会介绍基础算法，马上就发表dfs、bfs 最新最详细的讲解了，赶紧关注吧！

三、$DFS$的应用

(1).$DFS$由于有回溯的步骤，所以我们可以对其进行更新，比如并查集合并时的状态压缩都是使用$DFS$，还有图论中的 $tarjan$算法，$lca$等等。

(2)：搜索 有状态约束的 问题，比如说：
在一个给定形状的棋盘（形状可能是不规则的）上面摆放棋子，棋子没有区别。要求摆放时任意的两个棋子不能放在棋盘中的同一行或者同一列，请编程求解对于给定形状和大小的棋盘，摆放k个棋子的所有可行的摆放方案C。
Sample Input
4 4
…#
…#.
.#…
#…
Sample Output
1

题目要求：棋子只能放在#上并且 $k$个棋子必须在不同行不同列，所以说这里 进行了状态的限制，我们如果用$BFS$做肯定不太好做，但是我们刚好可以运用$DFS$的回溯特点做这个题目;
因为这个题目是二维的题目我们无法判断 该行该列到底有没有放棋子，我们只可以判断我们当前到的这一行放棋子了没有，于是我们在外面加一个数组$VIS$，它标记着第i列有没有放棋子，如果第$i$列放了棋子，那么我们就令 $vis[i]==true$。然后我们$dfs$他的每一行，在其间遍历他的每一列具体可能说不太清楚，我把代码和注释附上：

bool vis[50];
int n,k;
char mp[50][50];//标记每一列
/*AshGuang的版权*/
ll cnt=0;
void dfs(int x,int way)//用way记录我们放了多少棋子
{
    if(way==k)
    {
        cnt++;//cnt记录方案数
        return;//一定记得要return
    }
    if(x>=n) return;//这是判界 因为我们按行遍历，一共有n行不能多出去
    for(int i=0;i<n;i++)//判断这一行的每一列
    {
        if(mp[x][i]=='#'&&!vis[i])//如果说这mp[x][i]刚好是#而且 第i列没有放棋子 
        {
            vis[i]=1;//我们就放上
            dfs(x+1,way+1);//在下一行放，这一行已经无法放了，不同行不同列
            vis[i]=0;//这个地方比较关键，回溯的重点//注释1
        }
    }
    dfs(x+1,way);//这一行找不到的话就直接进行下一行//注释2
}
int main()
{
    while(~scanf("%d%d",&n,&k))
    {
        if(n==-1&&k==-1) break;
        cnt=0;
        memset(mp,0,sizeof(mp));
        for(int i=0;i<n;i++)
            scanf("%s",mp[i]);
        dfs(0,0);
        printf("%d\n",cnt);
    }
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

对于注释1的解释：因为我们根据题目要求 每一行每一列只能放一个棋子，那么如果这个棋子放在了当前这一行，我们就可以进入下一行搜索，那么这个搜索完成之后vis[i]=0，这个意义是什么呢？意思是这样的，当我们在这个根节点下 面所有的情况搜索完了之后，我们会回溯到这个结点，也就是说我们遍历完了 如果把 这个棋子放在 这一行这一列的 这个位置的时候，下面所有的状况，那么我们要进行 下一个状态搜索：也就是把棋子放在这一行的下一列的时候，那么这个时候 我们放的棋子绝对不是在这一列了，我们令这一列没有被标记过。
对于注释2的解释：这个有两个作用：

1. ① 如果这一行没有棋子可放我们可以跳到下一行继续搜索。
2. ②这一行有棋子可放我们可以遍历完这一行有棋子可放的情况，但是还有一种情况就是，这一行不放棋子，这也是可以的，因为只要到最后放够k个就足够了。

我们可以发现，要写这种$dfs$的话注意的细节还是很多的。

(3) 搜索联通块问题

比如说题目要求 一个矩阵中 只有1与0两种数字 ，问有几块儿1，对于块儿的定义：如果1的 九宫格范围内 也有1，那么这个1与 九宫格范围内的 1是一块儿，比如说：

1 0 1
0 1 0
1 0 1
输出：1

1 0 1 0 0
0 1 0 0 0
1 0 1 0 1
输出：2

这个问题是可以用 $BFS$来写的，但是容易超时，所以用$DFS$写最好不过了，根据$DFS$的特点，深度优先搜索嘛。我们对一个起点开始遍历他就会把他所有能按照要求到达的点 都遍历一遍。

伪代码：
从一个起点开始：
		该起点标记为1
		遍历该起点的每一个方向，如果是1，继续进行扩展延申
		结束之后，与该起点通过一定规则可以相连的都变成了1
		遍历下一个起点，遍历之前看看这个节点是否被标记过，没有cnt++；
具体代码：
void dfs(int x,int y,int id)
{
    if(x<1||x>m||y<1||y>n) return;
    if(num[x][y]||str[x][y]=='*') return;
    num[x][y]=id;
    for(int i=0;i<8;i++)
    {
        int mx=x+dx[i],my=y+dy[i];
        dfs(mx,my,id);
    }
}
  for(int i=1;i<=m;i++)
         for(int k=1;k<=n;k++)
               if(str[i][k]==1&&num[i][k]==0) dfs(i,k,++cnt);
  printf("%lld\n",cnt);
  最后cnt的值就是联通快个数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

四、$BFS$的简要应用

(1)：求最短路：

这个是图论里面的一种应用被称为SPFA算法，在我之前的博客中有总结过，所以在这里不再提。

(2)：求迷宫最短路：

这种题目用DFS也是可以解的，用 DFS的思路:有许多条路可以到达终点我们求一下 到达终点的最小值。这样是非常耗时间的 而BFS不一样因为BFS是按层遍历，所以 每一层对于根节点来说距离一定是最小的，不需要再次更新，我们到达终点时这个距离一定一定是最小的，比如说：

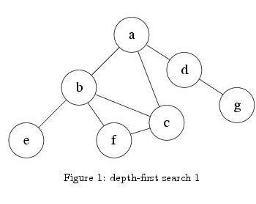
还是拿这张图来说 让我们求到达的C的最小距离，按照BFS的思路，第二层就可以到C我们直接break就可以了，为什么？因为如果a->b-f->c一定不会比直接到c近，这就是BFS最特殊的性质，在搜索过程中保留了最短路。所以我们用一个辅助数组来标记记录 到当前节点的 最小距离，如果 f还要访问c时，判断一下 如果 c这个地方的距离已经被更新，说明它已经确定了最小值，后来的无法更新，我们就不让c进入队列。这样一来最小值也就确定了。
拿一个例题来说，1代表墙壁，0代表可通路每次可以向四个方向出发，起点在左上方，终点在右下方，问最短距离：

伪代码：(用num[i][j]表示第i行第j个位置走过没有)
因为初始起点需要走0步，我们把num数组 初始-1，mem(num,-1)；
左上角为起点：
	num[1][1]=0;
	1 1进入队列
			取出当前队列第一个元素(因为二维通常需要使用结构体)
			判断它是否为终点位置？break：continue；
			遍历该点四个方向可行方向
				if(num[mx][my]==-1)
					num[mx][my]=num[i][k]+1
				把这个点进入队列。
	结束
具体代码：
int bfs()
{
	queue<node>q;
	q.push({1,1});
	num[1][1]=0;
	while(!q.empty)
	{
		node u=q.front();q.pop();//扔掉首元素
		for(int i=0;i<4;i++)
		{
			int mx=u.x+dx[i],my=u.y+dy[i];
			if(u.x==ex&&u.y==ey) return num[u.x][u.y];//放队列之前我们已经把距离更新了，只要找到这个点绝对是最小距离了。
			if(num[mx][my]==-1&&str[mx][my]==0)//这里还需要加一个判界，我就不手写了有点累了。
			{
				num[mx][my]=num[u.x][u.y]+1;
				q.push({mx,my});
			}
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

(3)：同时移动性题目问题：

火山在喷发，你在跑问是否可以跑出去。
详情之前解释过这个问题：Fire！

(4)：倒水问题：

每次倒水状态之间的转移，之前也有过例题：非常可乐！ 、$POJ341$pots

(5)：路径还原：

问从一个点到另一个点 的最短路径是多少，而题目不要求你输入最短距离，而是要求你还原路径这种时候通常需要加一个结构体数组来记录，其实上面的例题pots也是一个路径还原的问题，用一个简单的例题总结一下路径还原：
定义一个二维数组：

int maze[5][5] = {

0, 1, 0, 0, 0,

0, 1, 0, 1, 0,

0, 0, 0, 0, 0,

0, 1, 1, 1, 0,

0, 0, 0, 1, 0,
1
2
3
4
5
6
7
8
9

};

它表示一个迷宫，其中的1表示墙壁，0表示可以走的路，只能横着走或竖着走，不能斜着走，要求编程序找出从左上角到右下角的最短路线。
输出;
(0, 0)
(1, 0)
(2, 0)
(2, 1)
(2, 2)
(2, 3)
(2, 4)
(3, 4)
(4, 4)
我们定义结构体要加一个pre，记录它是由哪个点转移过来的：

#include <stdio.h>
#include <queue>
#include <algorithm>
#include <string.h>
using namespace std;
struct node{
    int x,y,pre;
}q[5000];
node save[5000];
int mp[50][50];
bool vis[50][50];
int my[6]={0,0,-1,1};
int mx[6]={-1,1,0,0};
int dis[50][50];
int head,cur;
int P;
int BFS()
{
    vis[1][1]=1;dis[1][1]=0;
    q[1].x=1;q[1].y=1;q[1].pre=-1;
    head=1;cur=1;
    while(head<=cur)//这是自己用数组写的队列，其实性质是一样的
    {
        int u=head;head++;
        if(q[u].x==5&&q[u].y==5)
        {
            P=u;
            return dis[q[u].x][q[u].y];
        }
        for(int i=0;i<4;i++)
        {
            int dx=q[u].x+mx[i];
            int dy=q[u].y+my[i];
            if(mp[dx][dy]||vis[dx][dy]||dx<1||dx>5||dy<1||dy>5)//判界
                continue;
            dis[dx][dy]=dis[q[u].x][q[u].y]+1;
            vis[dx][dy]=1;
            int nextN=++cur;
            q[nextN].x=dx;
            q[nextN].y=dy;
            q[nextN].pre=u;//记录这个状态转移而来的之前数组的下标。
        }
    }
}
输出时：只需要判断 对应下标的数组里面 存的是 x==1&&y==1就好了。
用回溯写：
void print(int a)
{
    if(q[a].x==1&&q[a].y==1)
    {
       printf("(%d, %d)\n",q[a].x-1,q[a].y-1);
       return;
    }
    else
    {
        print(q[a].pre);
        printf("(%d, %d)\n",q[a].x-1,q[a].y-1);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

五、总结

1. 到这里$dfs$与$bfs$的简要介绍与总结也就写完了，如果具体还不懂可以在下方留言，欢迎及时交流。

2. 任何有关侵犯版权问题，我都会及时道歉，谢谢宽容。

3. BFS与dfs各自都有优点，具体问题具体分析。

4. DFS的树的深度如果过长的话考虑用$BFS$而不去用$DFS$。
   2020.12.25update

   	                 人一我百，人十我万！加油！码农！
   1