基于深度学习的聚类算法综述_深度学习图像聚类

近年来，随着深度学习的发展，基于深度学习的聚类算法也得到了广泛的研究和应用。本文将介绍几种常见的基于深度学习的聚类算法，包括自编码器聚类、变分自编码器聚类、深度聚类网络、生成对抗网络聚类等，并给出相应的算法原理。

一、自编码器聚类

自编码器是一种无监督学习方法，可以将高维数据压缩成低维编码，并实现重构。自编码器聚类即将自编码器用于聚类问题，将编码作为簇的中心，将数据点分配到最近的簇中。自编码器聚类的优点是对于非线性数据具有较好的表达能力，缺点是需要手动设置簇的数量。

自编码器聚类的原理是通过自编码器将原始数据映射到低维空间，然后使用聚类算法将映射后的数据进行聚类。自编码器是一种由编码器和解码器组成的神经网络，编码器将原始数据映射到低维空间，解码器将映射后的数据重构成原始数据。自编码器聚类的过程是先训练自编码器，得到编码，然后使用聚类算法对编码进行聚类。

Matlab代码示例：

data = csvread('data.csv'); % 读取数据
input_size = size(data, 2); % 输入向量维度
hidden_size = 2; % 隐藏层维度
num_epochs = 100; % 训练轮数
batch_size = 32; % 批量大小

% 构建自编码器模型
autoencoder = trainAutoencoder(data', hidden_size, ...
    'MaxEpochs', num_epochs, 'BatchSize', batch_size);

% 得到编码
code = predict(autoencoder.Encoder, data');

% 进行K均值聚类
idx = kmeans(code, K);

% 绘制散点图
scatter(code(:,1), code(:,2), [], idx);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

二、变分自编码器聚类

变分自编码器是一种能够生成具有随机性的编码的自编码器，常用于图像生成和数据压缩等领域。变分自编码器聚类即将变分自编码器用于聚类问题，将生成的编码作为簇的中心，将数据点分配到最近的簇中。

变分自编码器聚类的原理是通过变分自编码器将原始数据映射到低维空间，然后使用聚类算法将映射后的数据进行聚类。变分自编码器是一种由编码器、解码器和隐变量网络组成的神经网络，隐变量网络生成随机噪声，编码器将原始数据和随机噪声映射到低维空间，解码器将映射后的数据和随机噪声重构成原始数据。变分自编码器聚类的过程是先训练变分自编码器，得到生成的编码，然后使用聚类算法对编码进行聚类。

Matlab代码示例：

data = csvread('data.csv'); % 读取数据
input_size = size(data, 2); % 输入向量维度
hidden_size = 2; % 隐藏层维度
num_epochs = 100; % 训练轮数
batch_size = 32; % 批量大小

% 构建变分自编码器模型
vae = trainVAE(data', hidden_size, ...
    'MaxEpochs', num_epochs, 'BatchSize', batch_size);

% 得到编码
code = vae.encode(data');

% 进行K均值聚类
idx = kmeans(code, K);

% 绘制散点图
scatter(code(:,1), code(:,2), [], idx);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

三、深度聚类网络

深度聚类网络是一种将深度学习和聚类相结合的无监督学习方法，可以自动学习特征表示和聚类结果。深度聚类网络的优点是可以处理非线性数据和高维数据，缺点是需要较长的训练时间和大量的计算资源。

深度聚类网络的原理是通过深度学习网络将原始数据映射到低维空间，然后使用聚类算法将映射后的数据进行聚类。深度聚类网络通常由编码器和聚类层组成，编码器将原始数据映射到低维空间，聚类层将编码作为簇的中心，将数据点分配到最近的簇中。深度聚类网络的过程是先训练深度学习网络，得到编码，然后使用聚类算法对编码进行聚类。

Matlab代码示例：

data = csvread('data.csv'); % 读取数据
input_size = size(data, 2); % 输入向量维度
hidden_size = 10; % 隐藏层维度
num_epochs = 100; % 训练轮数
batch_size = 32; % 批量大小

% 构建深度聚类网络模型
dlnet = dlnetwork([ ...
    fullyConnectedLayer(hidden_size, 'Name', 'fc1'), ...
    reluLayer('Name', 'relu1'), ...
    fullyConnectedLayer(hidden_size, 'Name', 'fc2'), ...
    reluLayer('Name', 'relu2'), ...
    fullyConnectedLayer(hidden_size, 'Name', 'fc3'), ...
    reluLayer('Name', 'relu3'), ...
    fullyConnectedLayer(hidden_size, 'Name', 'fc4'), ...
    reluLayer('Name', 'relu4'), ...
    fullyConnectedLayer(K, 'Name', 'fc5')]);

% 定义损失函数和优化器
lossFunc = @myLossFunction;
params = dlnet.Learnables;
lr = 0.001;
avgGradients = [];
avgVelocity = [];

% 训练模型
for epoch = 1:num_epochs
    idx = randperm(size(data, 1));
    for i = 1:batch_size:size(data, 1)
        inds = idx(i:min(i+batch_size-1, size(data, 1)));
        X = dlarray(data(inds, :)', 'SSCB');
        [grad, loss] = dlfeval(@myGradients, dlnet, X);
        [params, avgGradients, avgVelocity] = adamupdate(params, grad, avgGradients, avgVelocity, epoch, lr);
        dlnet = dlnetwork(params);
    end
    fprintf("Epoch %d loss: %f\n", epoch, double(gather(extractdata(loss))));
end

% 得到编码
code = predict(dlnet, dlarray(data', 'SSCB'));
code = extractdata(code)';

% 进行K均值聚类
idx = kmeans(code, K);

% 绘制散点图
scatter(code(:,1), code(:,2), [], idx);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

其中，myLossFunction和myGradients分别是自定义的损失函数和梯度函数。adamupdate是使用Adam优化器更新参数的函数。dlnetwork是Deep Learning Toolbox提供的深度学习网络类。

四、生成对抗网络聚类

生成对抗网络是一种能够生成具有随机性的样本的深度学习模型，常用于图像生成和数据压缩等领域。生成对抗网络聚类即将生成的样本作为簇的中心，将数据点分配到最近的簇中。生成对抗网络聚类的优点是对于非线性数据具有较好的表达能力，缺点是需要手动设置簇的数量。

生成对抗网络聚类的原理是通过生成对抗网络生成样本，然后使用聚类算法将生成的样本进行聚类。生成对抗网络由生成器和判别器组成，生成器生成具有随机性的样本，判别器判断样本是否为真实数据。生成对抗网络聚类的过程是先训练生成对抗网络，得到生成的样本，然后使用聚类算法对样本进行聚类。

以上是几种常见的基于深度学习的聚类算法及其原理。需要注意的是，聚类算法的效果很大程度上依赖于数据集的特点和参数的设置，需要根据实际情况进行调整。

Matlab代码示例：

data = csvread('data.csv'); % 读取数据
latent_size = 2; % 隐变量维度
num_epochs = 100; % 训练轮数
batch_size = 32; % 批量大小

% 构建生成对抗网络模型
gan = fitgmdist(data, K, ...
    'RegularizationValue', 0.1, 'CovarianceType', 'diagonal', 'SharedCovariance', true);

% 生成样本
samples = random(gan, size(data, 1));

% 进行K均值聚类
idx = kmeans(samples, K);

% 绘制散点图
scatter(samples(:,1), samples(:,2), [], idx);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

以上是几种常见的基于深度学习的聚类算法及其对应的Matlab代码示例。需要注意的是，聚类算法的效果很大程度上依赖于数据集的特点和参数的设置，需要根据实际情况进行调整。

五、 总结

深度聚类算法是一种利用深度学习的非线性表达和特征提取的能力进行聚类的算法模型，相比传统聚类算法更适合应用于拥有海量、高维的数据场景下。通过对这种方法的基本原理和优缺点的分析，可以加深对其作用机理的认识。

聚类算法的核心在于分辨数据之间的差异与共性。高维数据由于信息过多，导致传统聚类算法难以辨别数据之间的差异。例如经典的 K-means、谱聚类等算法在图像数据上往往得不到理想的结果。而深度聚类算法通过深度学习技术，使得提取的低维特征可以很好地保留原数据的信息与结构，减少了计算量的同时让数据的差异表现得更加明显，实现了更好的聚类效果。

基于不同自编码器的深度聚类算法侧重点各有不同，依据上文分析结果，表 1 从自编码器类型、创新、优势和局限性对这几类自编码器深度聚类算法做了对比分析：

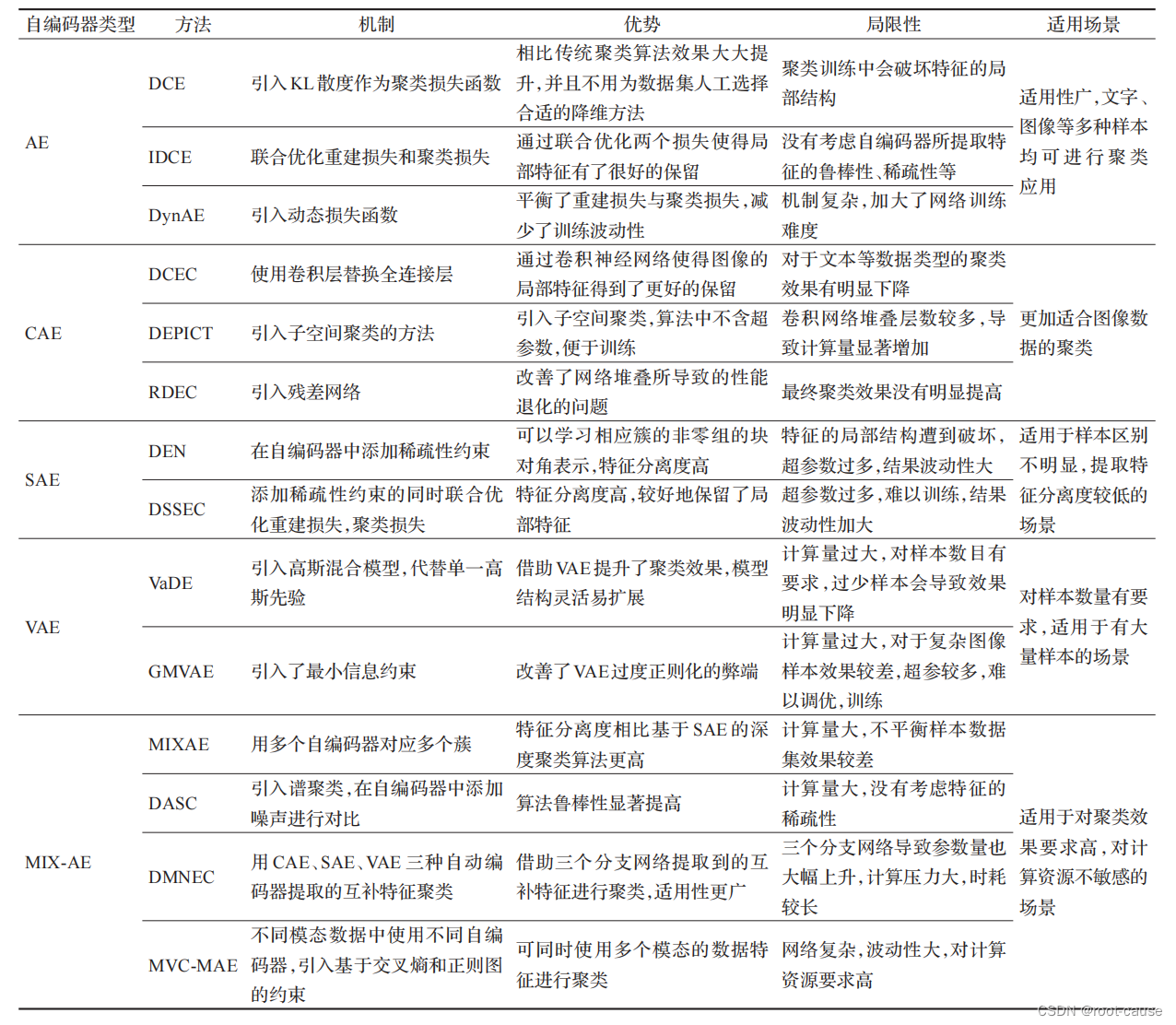
下面是对几种基于深度学习的聚类算法的优缺点总结：

自编码器聚类

• 优点：
  • 对于非线性数据具有较好的表达能力。
  • 可以通过自动编码器实现特征提取和聚类两个任务的联合训练。
  • 可以通过调整自编码器的参数来控制编码的维度。
• 缺点：
  • 需要手动设置簇的数量。
  • 对于复杂的数据集，聚类效果可能不佳。
  • 训练过程需要较长的时间和大量的计算资源。

变分自编码器聚类

• 优点：
  • 可以生成具有随机性的编码。
  • 可以通过变分自编码器实现特征提取和聚类两个任务的联合训练。
  • 可以通过调整变分自编码器的参数来控制编码的维度和随机性。
• 缺点：
  • 需要手动设置簇的数量。
  • 对于复杂的数据集，聚类效果可能不佳。
  • 训练过程需要较长的时间和大量的计算资源。

深度聚类网络

• 优点：
  • 可以自动学习特征表示和聚类结果。
  • 可以处理非线性数据和高维数据。
  • 可以通过调整网络结构和参数来控制聚类效果。
• 缺点：
  • 训练过程需要较长的时间和大量的计算资源。
  • 对于数据集的大小和质量要求较高。
  • 可能会出现过分聚类或欠分聚类的情况。

生成对抗网络聚类

• 优点：
  • 可以生成具有随机性的样本。
  • 对于非线性数据具有较好的表达能力。
  • 可以通过调整生成器的参数来控制样本的随机性和数量。
• 缺点：
  • 需要手动设置簇的数量。
  • 训练过程需要较长的时间和大量的计算资源。
  • 可能会出现样本分布不均匀的情况。

总的来说，选择哪种基于深度学习的聚类算法需要根据具体的数据集和需求来决定。在实际应用中，可以根据聚类效果、时间复杂度、可解释性等因素进行综合考虑。