【DL】《【Chatgpt】+【simplelatex】再也不用愁数学公式！！！》

《【Chatgpt】+【simplelatex】再也不用愁数学公式！！！》

1. 使用OCR工具解析公式：SimpleTex

示例：

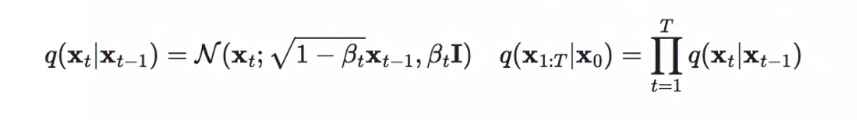
q(\mathbf x_t|\mathbf x_{t-1})=\mathcal N(\mathbf x_t;\sqrt{1-\beta_t}\mathbf x_{t-1},\beta_t\mathbf I)\quad q(\mathbf x_{1:T}|\mathbf x_0)=\prod\limits_{t=1}^T q(\mathbf x_t|{\mathbf x}_{t-1})\quad
1

2. 询问ChatGPT公式的含义

示例提示：

请解释如下公式：q(\mathbf x_t|\mathbf x_{t-1})=\mathcal N(\mathbf x_t;\sqrt{1-\beta_t}\mathbf x_{t-1},\beta_t\mathbf I)\quad q(\mathbf x_{1:T}|\mathbf x_0)=\prod\limits_{t=1}^T q(\mathbf x_t|{\mathbf x}_{t-1})\quad
1

示例输出：

这些公式是针对状态空间模型中的一个重要概率分布，即高斯分布（也称为正态分布）的一般形式。在状态空间模型中，高斯分布用于描述系统状态的不确定性，并且通常假定其满足马尔科夫性质，即当前状态只依赖于前一个状态。

公式中的 $\mathcal{N}({\mathbf{x}}_t;\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1},{\beta }_t\mathbf{I})$ 表示高斯分布的一般形式，其中 ${\mathbf{x}}_t$ 是当前状态的值，${\mathbf{x}}_{t-1}$ 是前一个状态的值，${\beta }_t$ 是一个常数（通常小于1），$\mathbf{I}$ 是单位矩阵。这个高斯分布的均值是 $\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1}$，表示当前状态的值以前一个状态的值为中心，而方差是 ${\beta }_t\mathbf{I}$，表示当前状态的值的不确定性。

公式中的 $q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)=\prod _{t=1}^{T}q({\mathbf{x}}_t|\mathbf{x}t-1)$ 表示根据前一个状态的值，生成当前状态的概率密度函数，这个概率密度函数是一个由 $T$ 个条件概率密度函数的连乘积组成的形式。在这个连乘积中，每个条件概率密度函数 $q({\mathbf{x}}_t|\mathbf{x}t-1)$ 都表示在给定前一个状态 ${\mathbf{x}}_{t-1}$ 的情况下，生成当前状态 ${\mathbf{x}}_t$ 的概率密度函数。在这个公式中，假定状态满足马尔科夫性质，即当前状态只依赖于前一个状态，因此 $q({\mathbf{x}}_t|\mathbf{x}t-1)$ 只依赖于前一个状态 $\mathbf{x}t-1$。