[双指针]统计子矩阵 2022年蓝桥杯_mxn的矩阵有多少个子矩阵

题目描述

给定一个 N × M 的矩阵 A，请你统计有多少个子矩阵 (最小 1 × 1，最大 N × M) 满足子矩阵中所有数的和不超过给定的整数 K?

输入

第一行包含三个整数 N, M 和 K.

之后 N 行每行包含 M 个整数，代表矩阵 A.

输出

一个整数代表答案。

样例输入

3 4 10
1 2 3 4
5 6 7 8
9 10 11 12

样例输出

19

提示

满足条件的子矩阵一共有 19，包含：

大小为 1 × 1 的有 10 个。

大小为 1 × 2 的有 3 个。

大小为 1 × 3 的有 2 个。

大小为 1 × 4 的有 1 个。

大小为 2 × 1 的有 3 个。

对于 30% 的数据，N, M ≤ 20.

对于 70% 的数据，N, M ≤ 100.

对于 100% 的数据，1 ≤ N, M ≤ 500; 0 ≤ Ai j ≤ 1000; 1 ≤ K ≤ 250000000.

题意： 题意很明确，就是从n*m的矩阵中找到有多少个和小于等于k的子矩阵。

分析： 直接暴力是O(n^4)，只能过70%数据，而要想满分就需要一些技巧上的优化。如果还是按照二维前缀和的思路走下去其实并不好优化，这里需要换一种枚举矩阵的思路，一个矩阵由两维确定，可以先枚举出一维的区间，然后在其中枚举另一维区间，第一次枚举是O(n^2)的，而第二次枚举就可以用双指针优化成O(n)了，思路类似于求区间和不大于k的子段个数。

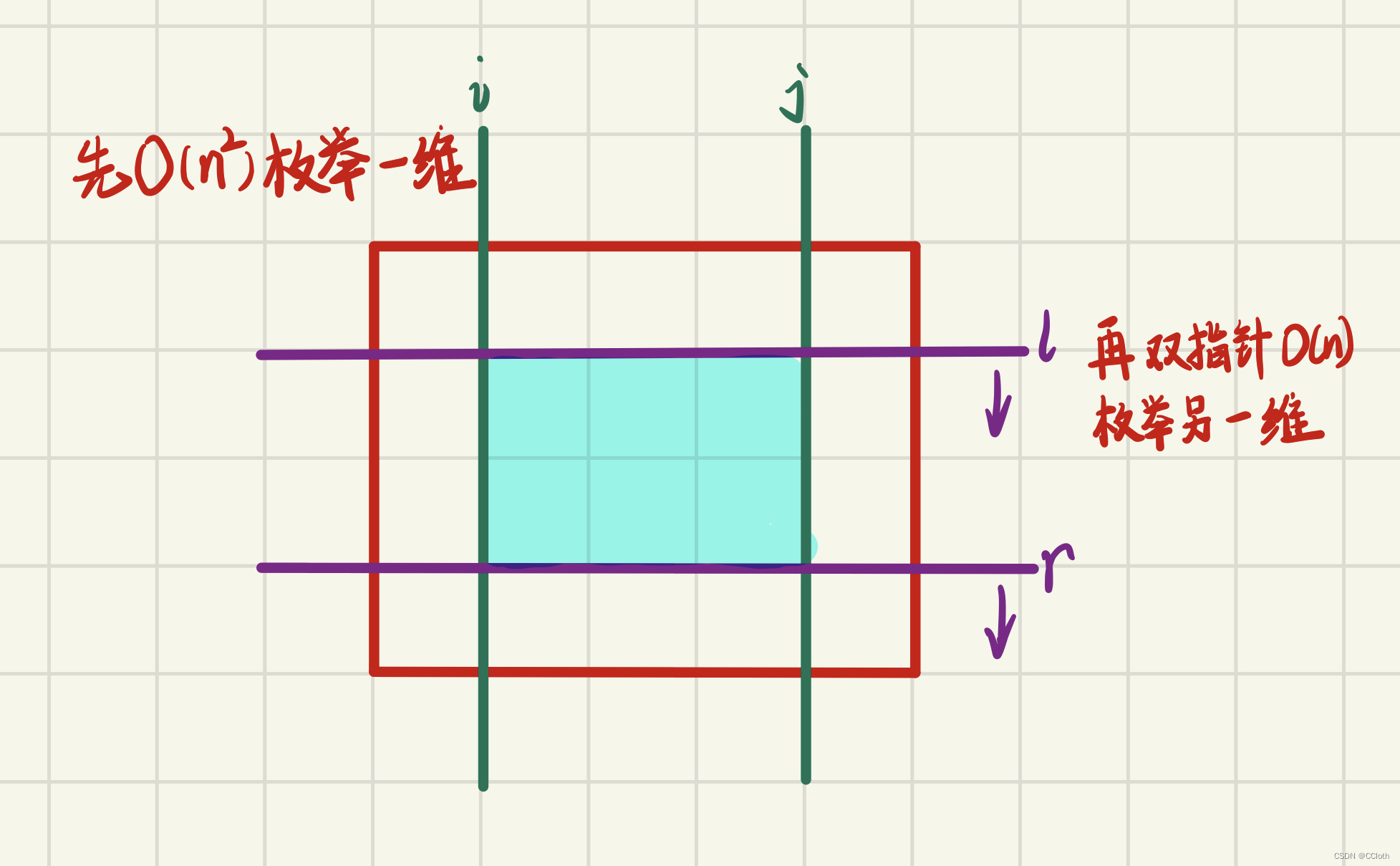
具体代码如下：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <string>
#define int long long
using namespace std;
//子矩阵个数最多为500*500*500*500/2，所以要开long long 
int a[505][505], s[505][505];//s[i][j]表示第i行各数的前缀和 
int n, m, k;
 
signed main()
{
	cin >> n >> m >> k;
	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= m; j++){
			scanf("%lld", &a[i][j]);
			s[i][j] = s[i][j-1]+a[i][j];
		}
	int num = 0;
	for(int i = 1; i <= m; i++)
		for(int j = i; j <= m; j++){
			int sum = 0;
			for(int l = 1, r = 1; r <= n; r++){
				sum += s[r][j]-s[r][i-1];
				while(sum > k){
					sum -= s[l][j]-s[l][i-1];
					l++;
				}
				num += r-l+1;
			}
		}
	cout << num;
    return 0;
}