- 1Baidu Comate中文名——文心快码——送礼物来了(活动最后3天)_如何登入 文心快码
- 2从“专家”视角看:2024年软件测试行业的八大发展趋势!_列举在ai自动化测试工具链领域,国外软件的龙头以及国产化软件的龙头
- 3Stable Diffusion【二次元模型】:质量高细节丰富的动漫风格大模型anima_pencil-XL_animapencilxl
- 4vue 视频添加水印_vue3视频点播嵌入水印
- 5Python 中的后台进程_python后台运行
- 6AIGC各个应用场景下的模型选择
- 7win10家庭版安装Docker_windows10家庭版安装docker
- 8三天吃透Redis面试八股文
- 9php如何判断0和空_php判断0和空值
- 10python-learning20--高阶教程--基础阶段--python字符串--拼接操作
《RWKV》论文笔记
赞
踩
原文出处
[2305.13048] RWKV: Reinventing RNNs for the Transformer Era (arxiv.org)
原文笔记
What
RWKV(RawKuv):Reinventing RNNs for the Transformer Era
本文贡献如下:
提出了 RWKV 网络架构,结合了RNNS 和Transformer 的优点,同时缓解了它们已知的限制
我们提出了一种新的线性注意力机制
展示了 RWKV 在处理涉及大规模模型和长距离依赖关系的任务时的性能、效率和扩展能力
RWKV的突出卖点:
O(1)推理复杂度真的非常香
- 单 token 推理时间恒定,总推理时间随序列长度线性增加
- 内存占用恒定,不随序列长度增加
- 推理时间和内存占用随模型尺寸线性增长
优势是数量级级别的,这意味着:
- 大模型的硬件限制和部署成本将大幅降低,CPU及非 NV 加速卡均可部署
- 服务器上部署大模型的成本将大幅降低,普通台式机和笔记本将能在本地部署大模型手机端部署也成为可能
RWKV 将推动大模型进行一次架构迁移!
Why
Transformer具有出色的序列建模能力,一次处理一整句话,或一整段话,可以并行训练,但是同样面临着计算复杂度高,内存占用大,计算成本高的难题
传统的Transformer的总推理时间随序列长度二次增加(在序列特别长的情况下有可能三次增加)
自注意力机制的二次复杂度使其成为涉及长序列和受限资源的任务的计算和内存密集型。这刺激了增强 Transformer 可扩展性的研究,有时牺牲了一些其有效性
循环神经网络 (RNN) 在内存和计算需求方面表现出线性缩放,内存占用小,计算量小,(因为他每次只处理一部的数据)但由于并行化和可扩展性的限制,难以与 Transformer 匹配相同的性能。
RNN在训练长序列时容易出现梯度消失问题
RNN 在训练过程中对前一步结果依赖,无法在时间维度上进行并行化,限制了其可扩展性(无法获得很大的rnn模型)
RWKV 背后的动机是平衡计算效率和神经网络的表达能力。它提供了一种处理具有数十亿个参数的大规模模型的解决方案,以降低计算成本表现出具有竞争力的性能。实验表明,RWKV 解决了 AI 中的缩放和部署挑战,特别是对于顺序数据处理,指向更可持续和高效 AI 模型。
Challenge
Idea
model
容我再整理整理
原文翻译
Abstract
Transformers 彻底改变了几乎所有自然语言处理 (NLP) 任务,但受到内存和计算复杂性的影响,这些复杂性随序列长度呈二次方扩展。相比之下,循环神经网络 (RNN) 在内存和计算需求方面表现出线性缩放,但由于并行化和可扩展性的限制,难以与 Transformer 匹配相同的性能。我们提出了一种新颖的模型架构,即感知加权键值 (RWKV),它将变压器的高效并行训练与 RNN 的有效推理相结合。
我们的方法利用了线性注意力机制,并允许我们将模型制定为 Transformer 或 RNN,从而在训练期间并行化计算并在推理过程中保持恒定的计算和内存复杂性。到目前为止,我们将我们的模型扩展到多达 14 亿个参数,是迄今为止训练的最大密集 RNN,发现 RWKV 的性能与类似大小的 Transformer 相当,这表明未来的工作可以利用这种架构来创建更有效的模型。这项工作为协调序列处理任务中计算效率和模型性能之间的权衡迈出了重要的一步。
Introduction
深度学习极大地推动了人工智能,影响了一系列科学和工业用途。这些通常涉及复杂的顺序数据处理任务比如自然语言理解任务,会话AI,时间序列分析,和间接顺序格式,如图像和图表(Brown等人,2020;Ismail Fawaz等人,2019;Wu等人,2020;Albalak等人,2022)。这些技术中占主导地位包括 RNN 和 Transformers (Vaswani et al., 2017),每种都有特定的优点和缺点。RNN 需要更少的内存,特别是对于处理长序列。然而,它们在训练过程中在时间维度上存在梯度消失问题和非并行性,限制了它们的可扩展性(Hochreiter,1998;Le 和 Zuidema,2016)。
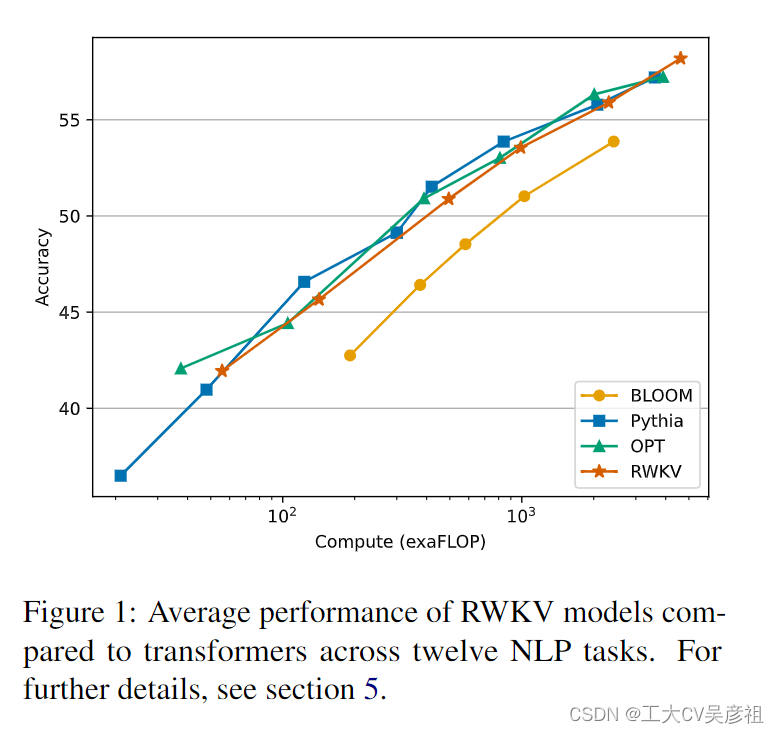
Transformers 已经成为一种强大的替代方案,擅长管理局部和远程依赖项并支持并行训练(Tay 等人,2022 年)。诸如GPT-3 (Brown et al., 2020)、ChatGPT (OpenAI, 2022;Kocón et al., 2023),LLAMA (Touvron et al., 2023) 和 Chinchilla (Hoffmann et al., 2022) 展示了 Transformer 在 NLP 中的潜力。然而,自注意力机制的二次复杂度使其成为涉及长序列和受限资源的任务的计算和内存密集型。这刺激了增强 Transformer 可扩展性的研究,有时牺牲了一些其有效性(Wang 等人,2020;Zaheer 等人,2020;Dao 等人,2022a)。
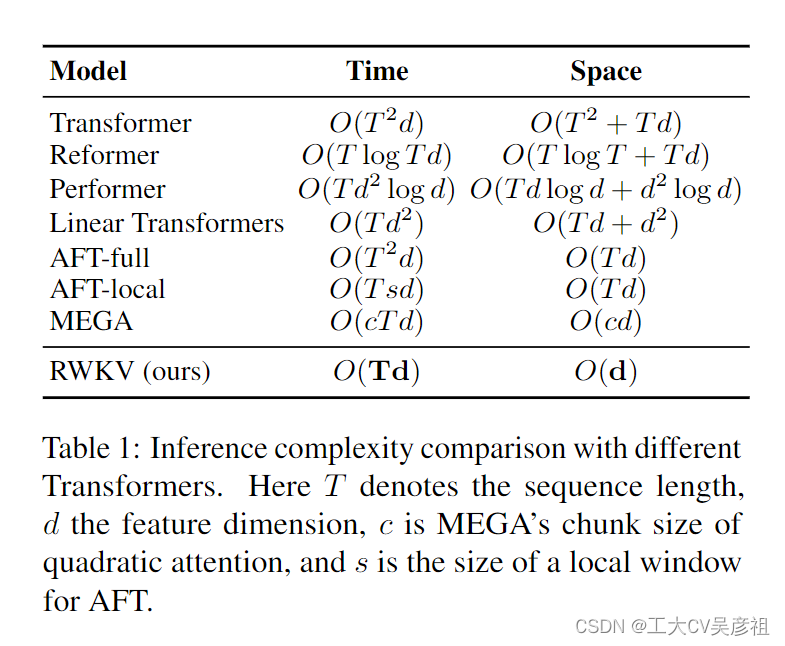
为了应对这些挑战,我们引入了感知加权键值 (RWKV) 模型,结合了 RNN 和 Transformer 的优势,同时规避了关键缺陷。RWKV 通过高效的线性缩放缓解了与 Transformer (Katharopoulos et al., 2020) 相关的内存瓶颈和二次缩放,同时保持 Transformer 的表达能力,例如并行训练和鲁棒可扩展性。RWKV 用线性注意力的变体重新制定注意力机制,用更有效的通道定向注意力替换传统的点积令牌交互。这种实现,没有近似,提供了最低的计算和内存复杂性;见表 1。
RWKV 背后的动机是平衡计算效率和神经网络的表达能力。它提供了一种处理具有数十亿个参数的大规模模型的解决方案,以降低计算成本表现出具有竞争力的性能。实验表明,RWKV 解决了 AI 中的缩放和部署挑战,特别是对于顺序数据处理,指向更可持续和高效 AI 模型。我们在本文中的贡献如下:
- RWKV 的引入,一种新颖的架构,结合了 RNN 和 Transformer 优势,同时减轻了它们的局限性。
- 详细的实验,展示了 RWKV 在大规模模型的基准数据集上的性能和效率。
- 预训练模型的释放,从 1690 万个参数到 14 亿个参数,在 Pile 上训练(Gao 等人,2020;Biderman 等人,2022)。
2 Background
在这里,我们简要回顾了 RNN 和 Transformer 的基本原理。
2.1 Recurrent Neural Networks (RNNs)
LSTM (Hochreiter and Schmidhuber, 1997) 和 GRU (Chung et al., 2014) 等流行的 RNN 架构的原理可以概括为以下公式(如 LSTM 所示,其他架构可以类似地推理):
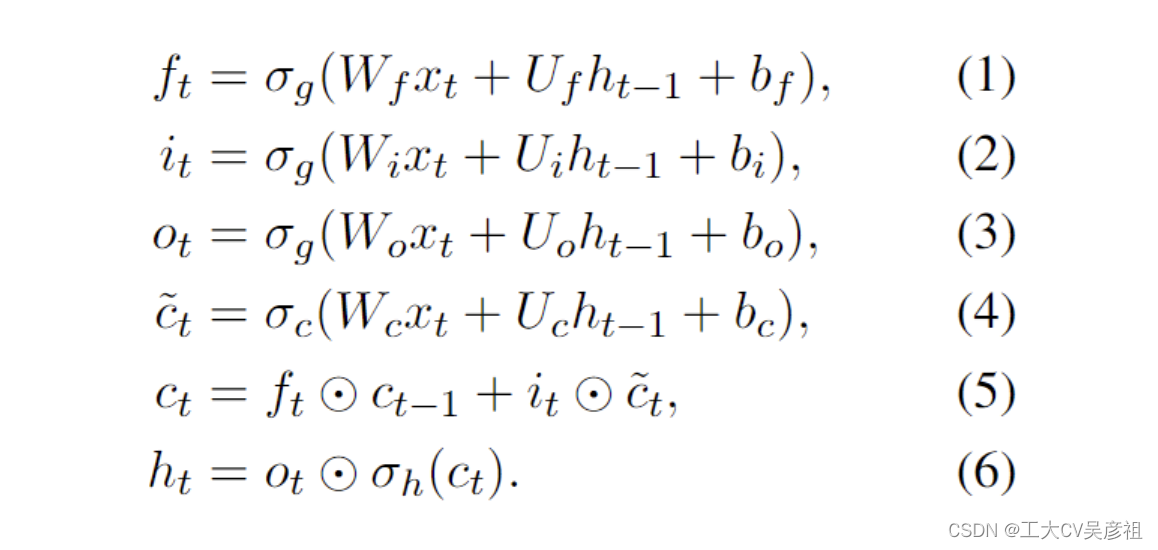
尽管RNN可以分解为两个线性块(W和U)和一个特定于RNN的块(1)-(6),如Bradbury等人所述。(2017),依赖于先前时间步长的数据依赖禁止并行化这些典型的RNN。
2.2 Transformers and AFT
由Vaswani等人(2017)介绍,Transformers是一类神经网络,已经成为几个NLP任务的主要架构。Transformer 不是像 RNN 那样逐步操作序列,而是依靠注意力机制来捕获所有输入和输出tokens之间的关系:
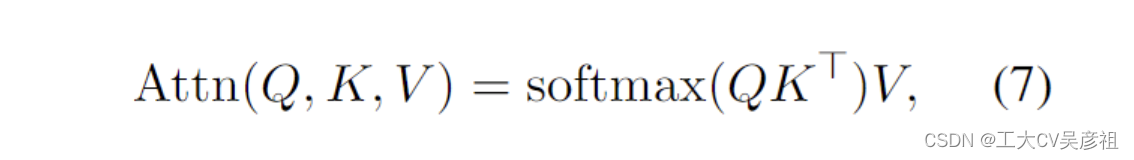
其中为方便起见,省略了多头和比例因子 1√dkis。核心 QK⊤ 乘法是一个在序列中的每个令牌之间成对注意力分数的集合,可以分解为向量操作:
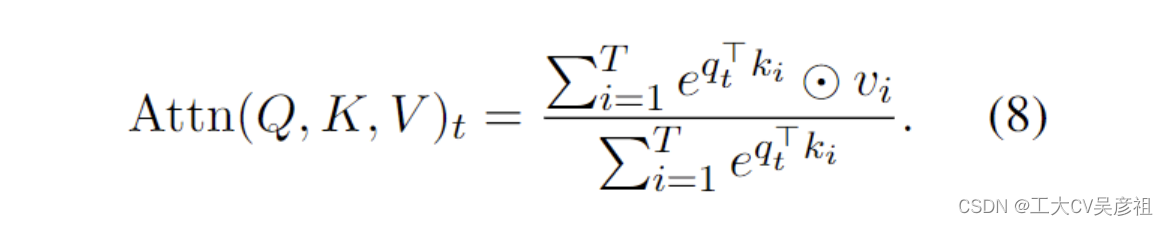
AFT (Zhai et al., 2021),表述为
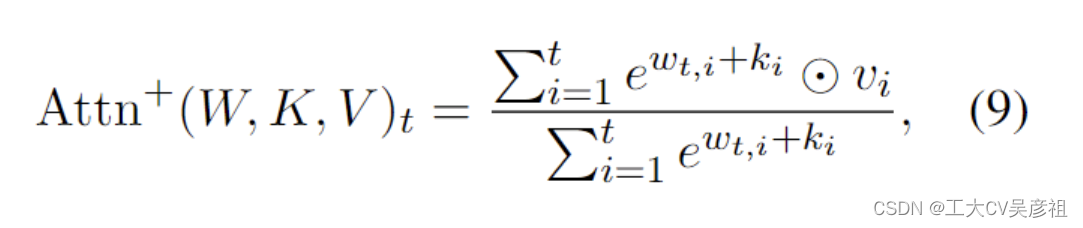
其中 {wt,i} ∈ RT ×T 是学习的成对位置偏差,每个 wt,i 是一个标量。
受 AFT 的启发,RWKV 采用类似的方法。但是,为简单起见,它修改了交互权重,使其可以转化为 RNN。RWKV 中的每个 wt,i 是一个通道时间衰减向量乘以相对位置并从当前时间向后跟踪,因为它衰减:
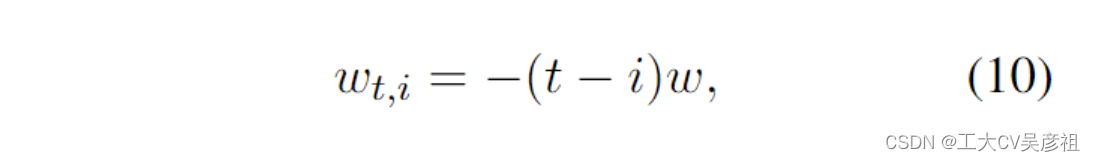
其中 w ∈ (R≥0)^d,d 是通道数。我们要求 w 是非负的,以确保 e^wt,i ≤ 1 并且每通道权重在时间上向后衰减。
距离当前token越远的token它就会衰减的越多,越近的token它就会衰减的越少,但实际情况比这个还要复杂一点,后边有个图来可视化这一部分(channel的信息衰减))
3 RWKV
RWKV模型架构由四个基本元素构成,这四个基本元素本质上都是时间混合的和通道混合的:
R:Receptance向量充当过去信息的接收器(作为过去信息的接受程度的接受向量)
W:Weight表示位置权重衰减向量,即模型中的可训练参数(可训练的模型参数)
K:键向量,类似于传统注意力机制中的K。(用每一个token自身的一个值来对位置向量进行调制)
V:值向量,类似于传统注意力机制中的V。
这些核心元素在每个时间步乘法交互,如图 2 所示。

3.1 Architecture
RWKV 模型由堆叠的残差块组成。每个块由一个时间混合和一个通道混合子块组成,实现循环结构以利用过去的信息。
该模型使用了独特的类似注意力的分数更新过程,其中包括一个随时间变化的 softmax 操作,以提高数值稳定性和减轻消失梯度(对于严格的证明,请参见附录 H)。它确保梯度沿着最相关的路径传播。此外,架构中包含的层归一化 (Ba et al., 2016) 有助于稳定梯度,有效地解决梯度消失和爆炸的问题。这些设计元素不仅增强了深度神经网络的训练动态,而且促进了多层的堆叠,通过捕获不同抽象级别的复杂模式,从而比传统的 RNN 模型具有更好的性能(另见附录 I)。
3.1.1 Token Shift
在该架构中,计算中涉及的所有线性投影向量(R, K, V,通道混合中的R ', K ')都是通过当前时间步输入和前一个时间步输入之间的线性插值产生的,促进令牌移位。
时间混合计算的向量是块当前输入和先前输入的线性组合的线性投影:

通道混合输入也是如此:

使用 PyTorch (Paszke et al., 2019) 库 asnn 在每个块的时间维度上实现令牌移位作为一个简单的偏移量。ZeroPad2d((0,0,1,-1))。
(在模型参数较小的时候与Transofrmer的效果还是有一定差距的)
3.1.2 WKV Operator
我们模型中的 W KV 算子的计算与 Attention Free Transformer (AFT) 中使用的方法并行(Zhai 等人,2021 年)。然而,与 W 是一个成对矩阵的 AFT 不同,我们的模型将 W 视为由相对位置修改的通道向量。在我们的模型中,这种循环行为由 W KV 向量的时间相关更新定义,形式化如下等式:

为了规避 W 的任何潜在退化,我们引入了一个单独关注当前标记的向量 U。有关这方面的更多信息可以在附录 I 中找到。
3.1.3 Output Gating
使用 sigmoid 在时间混合和通道混合块中实现输出门控,接受度,σ(r)。W KV 算子后输出向量 ot 由下式给出:

3.2 Transformer-like Training
RWKV 可以使用一种称为时间并行模式的技术有效地并行化,让人想起 Transformer。在单个层中处理一批序列的时间复杂度为 O(BT d2),主要由矩阵乘法 Wλ 组成,其中 λ ∈ {r, k, v, o}(假设 B 序列、Tmaximum 标记和 d 个通道)。相比之下,更新注意力分数wkvt涉及串行扫描(更多细节见附录D),复杂度为O(BT d)。矩阵乘法可以类似于 Wλ 并行化,其中传统 Transformer 中的 λ ∈ {Q, K, V, O}。逐元素 W KV 计算依赖于时间,但可以很容易地沿其他两个维度并行化 (Lei et al., 2018)3。
3.3 RNN-like Inference
循环网络通常利用状态 t 的输出作为状态 t + 1 的输入。在语言模型的自回归解码推理中也可以观察到这种用法,其中每个令牌必须在传递到下一步之前计算。RWKV 利用了这种类似 RNN 的结构,称为时间顺序模式。在这种情况下,RWKV 可以方便地在推理过程中递归制定用于解码,如附录 D 所示。
下略


