- 1Sqlite创建database的两种方法,以及源码分析,以及抽象类如何在SqliteHelper中应用_sqlite create database
- 2前端高级进阶13本经典书籍_c# 2023进阶图书
- 3【Spark】Spark SQL 数据类型转换_spark 字段类型,高级大数据开发开发面试解答之线程篇_spark sql类型转换
- 4vue+openLayers闪烁图形/线段/点 都可以使用类似的方法_openlayers 闪烁点
- 5vue3+vite 代码混淆插件_rollup-plugin-obfuscator
- 6【Python设计模式07】工厂方法模式
- 7Android jetpack viewModel 屏幕旋转数据如何保存。_jetpack+旋转后保持数据
- 8postman做接口测试12-请求前置脚本_postman 前置操作执行完成后调用
- 9基于FFmpeg进行rtsp推流及拉流(详细教程)_ffmpeg推流
- 10史上最“脑残”的“抢火车票”程序(node.js版)_node抢票脚本
三维重建(1)--摄像机几何_齐次坐标系相机坐标投影矩阵
赞
踩
目录
一、摄像机设计
摄像机的设计是为了记录我们的世界,如果在实物场景面前放一个胶片的话,实物不同位置的光线会交错到同一点,导致模糊,这也就是在一般的散射光或者平行光照下不会自然成像的原因。
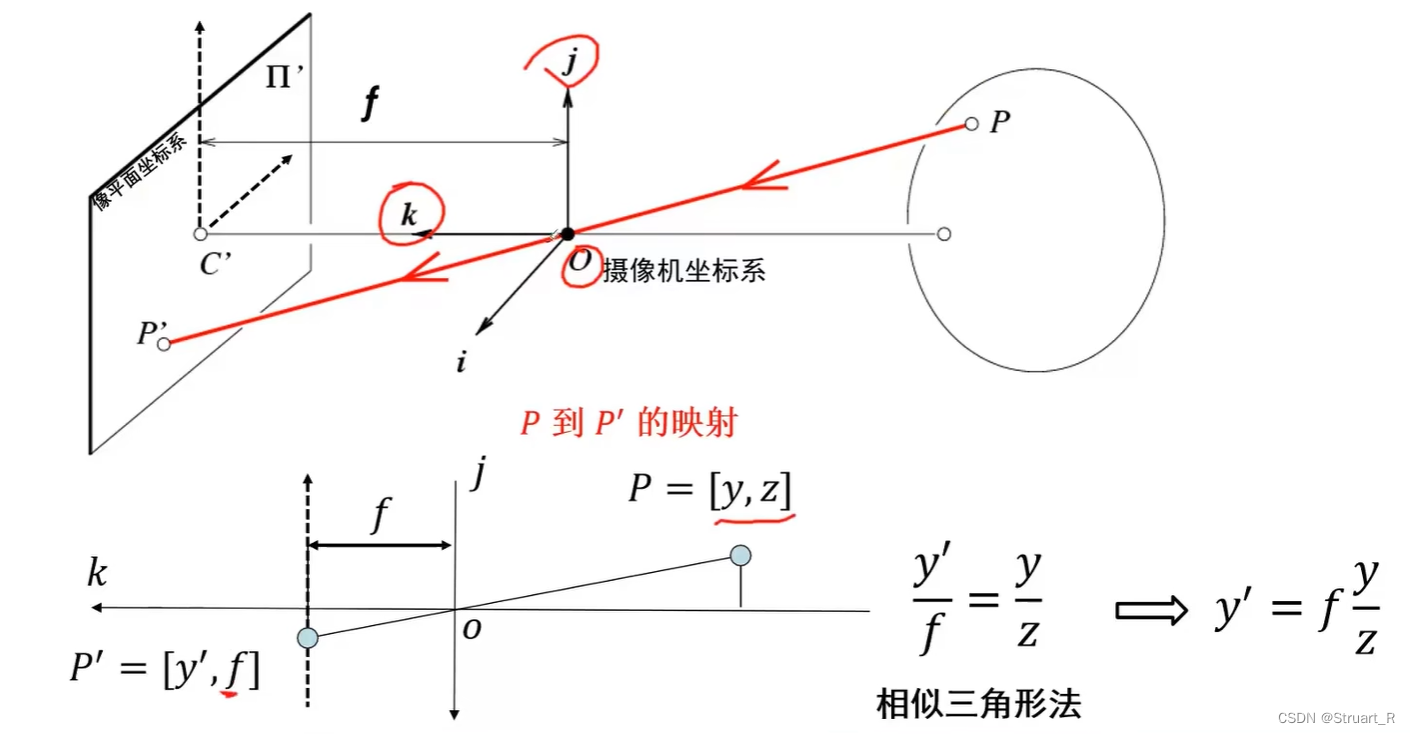
1、针孔摄像机
针孔摄像机就是小孔成像原理,通过孔的缝隙筛掉一部分多余的光线,使成像清晰。
小孔成像中根据孔所在平面将空间分为两个半平面,在实物一侧可以看到虚像,实物的对侧可以看到实像(像平面)。
在针孔摄像机中,定义实像和小孔之间的距离叫做焦距。

针孔摄像机坐标系, 实物侧为三维坐标P,像平面侧为二维坐标P',相当于实物通过摄像机作了一个二维投影到像平面坐标上,满足相似三角形关系,此时还没有考虑摄像机坐标,摄像机旋转等问题。
此时假设实物为,像为
,满足映射关系
。
光圈对摄像机的影响:光圈减小,成像越清晰,成像越暗。
2、透镜摄像机
透镜摄像机可以将多条光线汇聚到胶片上,增加照片亮度。
在透镜摄像机中定义透镜与汇聚点之间的距离为焦距。
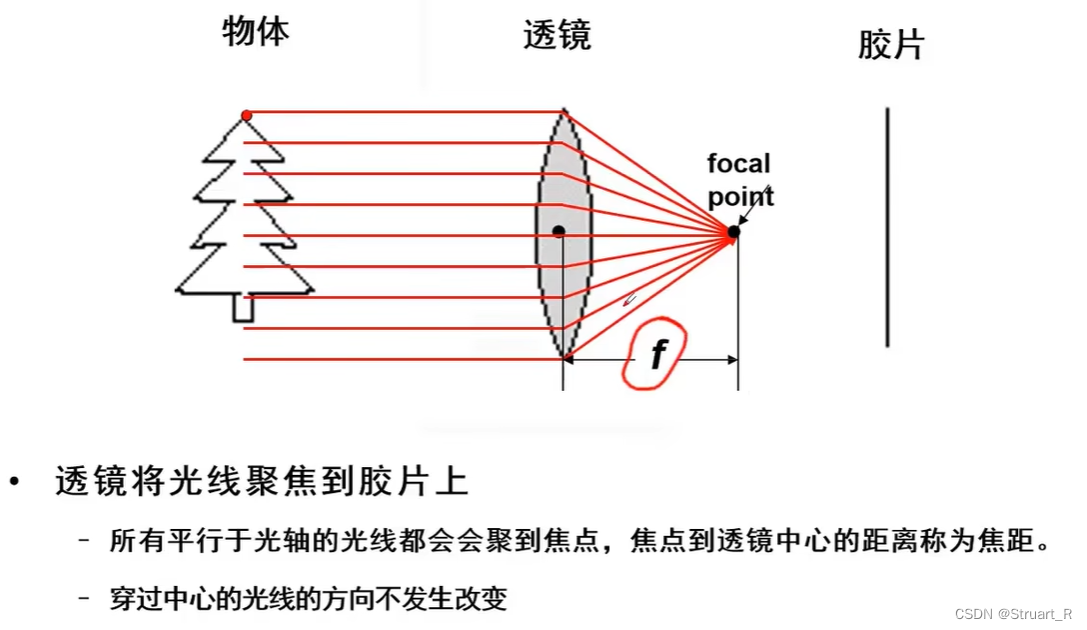
近轴折射模型:用于描述光线在透镜上折射的物理现象的现象,可以通过物体的在现实世界的坐标推导胶片上的坐标。
此时的物体与像之间的映射关系有所变化,原来的比例系数是焦距f,而透镜摄像机重新定义焦距,此时比例系数为透镜到胶片的距离,不是透镜到物体的距离。

3、失焦
失焦是透镜摄像机经常出现的一个问题,由于大物体的不同区域相距摄像机的距离不同,在有限景深范围内,会导致部分物体失焦的现象,例如将焦距调至刚好对于近距离区域清晰,而此时远距离的区域会出现模糊的情况。
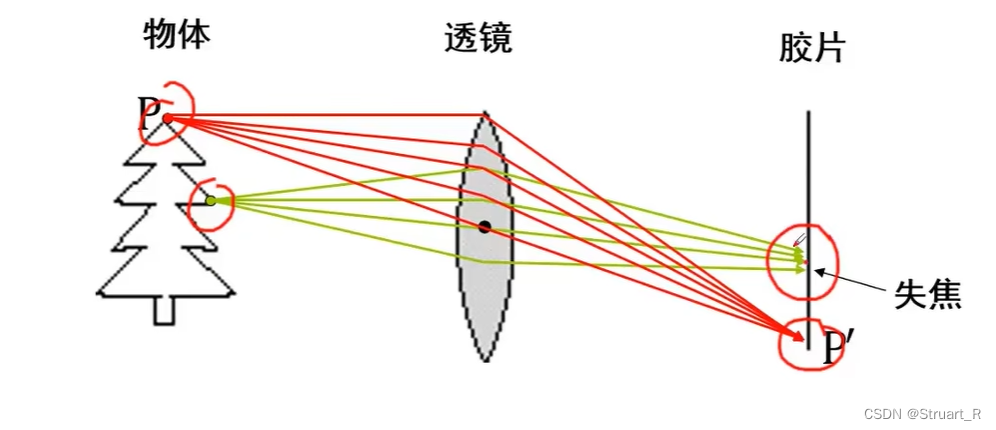
失焦也在摄影中有广泛的应用,比如微距摄影。
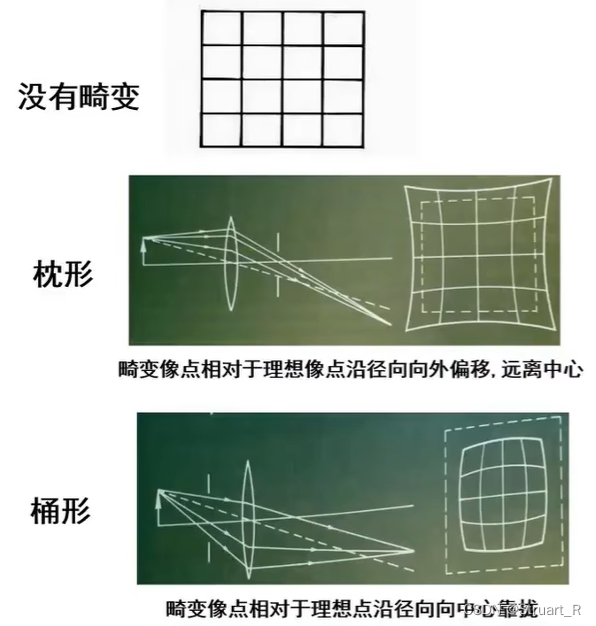
4、畸变
畸变:由于透镜的光学性质,透镜的安装不规范,透镜缺陷,导致透镜对物体所成的像出现失真,扭曲的现象。畸变一共分为三种,径向畸变、切向畸变、薄透镜畸变。
径向畸变:由于透镜边缘区域和中心区域放大倍率不同而导致,这种畸变的影响最大,一般分为枕形畸变和桶形畸变。
切向畸变:由于透镜安装与成像平面不平行而导致,会出现远大近小,圆变椭圆的情况。这种畸变通过正确安装是可以避免的。
薄透镜畸变:透镜设计缺陷和加工误差而导致,一般忽略不计。
二、摄像机几何
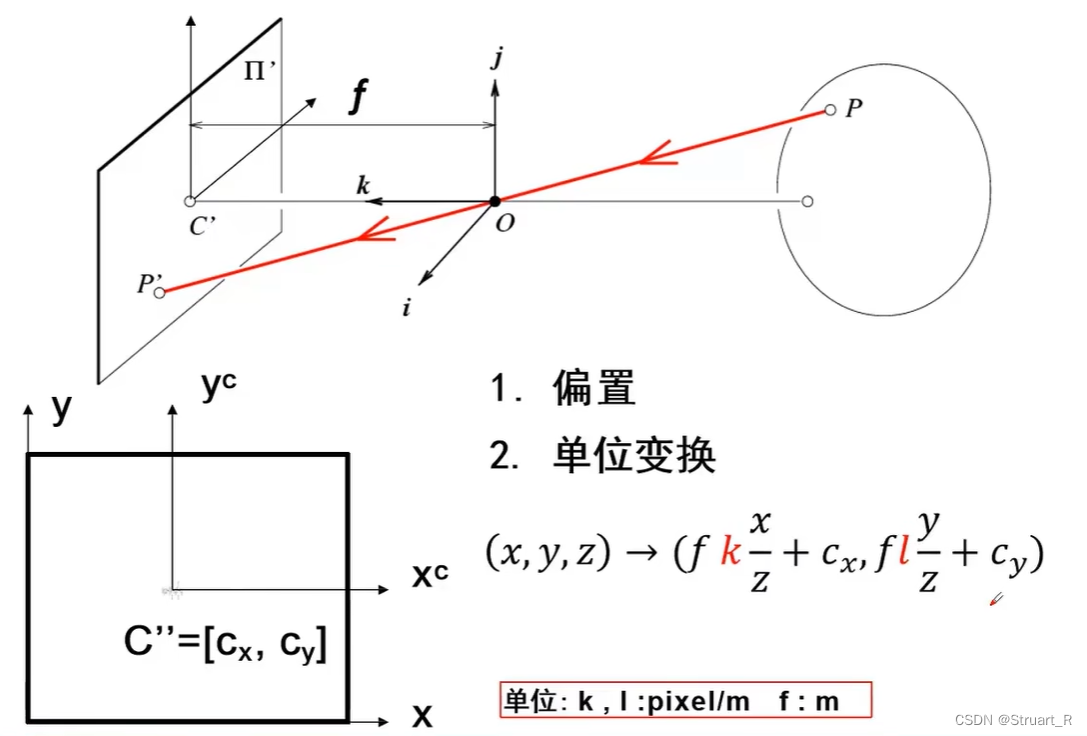
1、像素坐标系
像素坐标系相较于透镜摄像机的映射关系添加了偏置和单位变换两项。
(1)偏置
由于像平面的坐标变换,一般来说左下角为原点,那么投影到像平面上应该加上平移变换的。
(2)单位变换
由于像素坐标系是以一个像素点为单位,而不是像坐标系是一个二维坐标系以m或mm为单位,所以要引入坐标变换参数k和l,单位是pixel/m,其中分母m也可以换成其他长度单位mm、cm等,另外k和l两个参数的单位也不一定相同,有可能存在伸缩变换。
最终的映射关系为:。
一般来说,fk和fl会简化为α和β,就有下面映射关系成立:
P到P'的变换是线性的吗?
答案:不是线性的,由于x、y变化时z也有可能变化,z并不是一个恒定的常数,所以并不是线性的。
2、齐次坐标
齐次坐标可以简化摄像机几何中的计算和表示,在原有的二维坐标和三维坐标上增广一个单位1,就转换为齐次坐标。二维坐标增广为三行列向量,三维坐标增广为四行列向量。
将齐次坐标转换为一般坐标的方法,就是将除了列向量的最后一行,其余行都分别除以最后一行,保留其余行作为一般坐标,达到减少一行的目的,转换为了一般坐标。

如何利用齐次坐标系进行投影变换?
下面表达式中代表物体的齐次坐标形式,
代表像的齐次坐标形式,
与
之间通过一个三行四列的矩阵M进行变换。
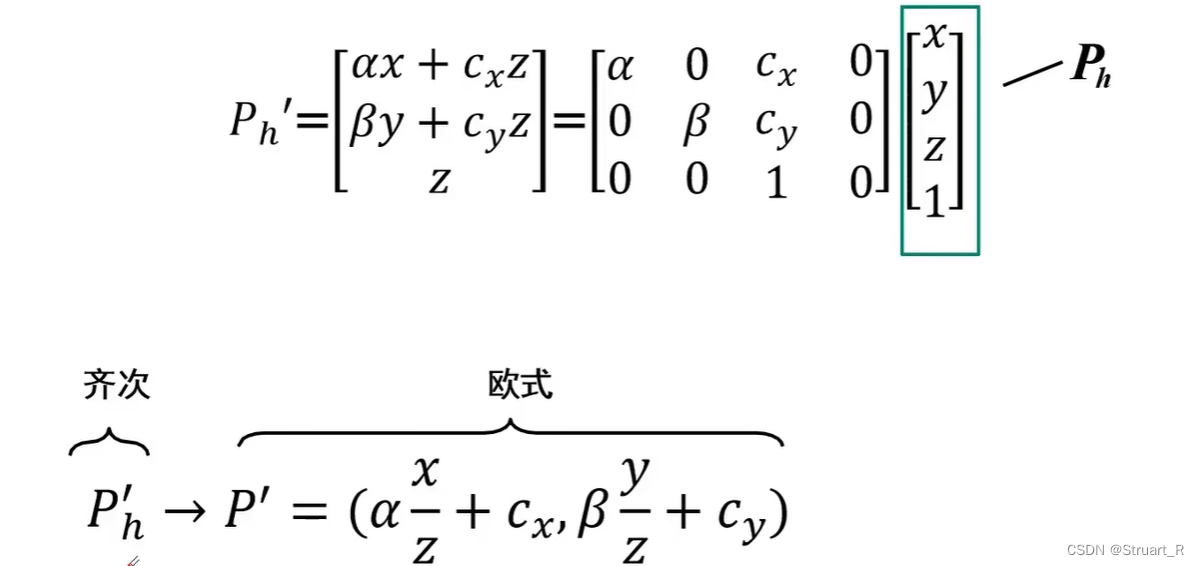
对于后面的介绍,如果没有特殊说明,所有坐标一律按照齐次坐标表示,也不再使用下标h进行标识。
3、摄像机偏斜
由于存在摄像机偏斜,像素块不是一般的方形而是平行四边形,此时像素平面存在了夹角θ,如下图所示,此时变换矩阵M也要做出相应的改进。

4、摄像机坐标系下的摄像机模型
在此模型下没有引入摄像机与世界坐标之间的转换关系,即物体可能存在平移旋转的外参数。
在摄像机坐标系下,投影矩阵即矩阵M为三行四列矩阵,定义摄像机内参数矩阵K(α、β、θ、、
五个参数)为三行三列矩阵,去除右侧的一列0,那么P'和P之间的关系就为
,
指的是三维单位矩阵加一列0的三行四列矩阵形式。

5、规范化摄像机
规范化摄像机指的是投影矩阵M为的形式,此时,物体坐标只比像素坐标多了最后一行的1。
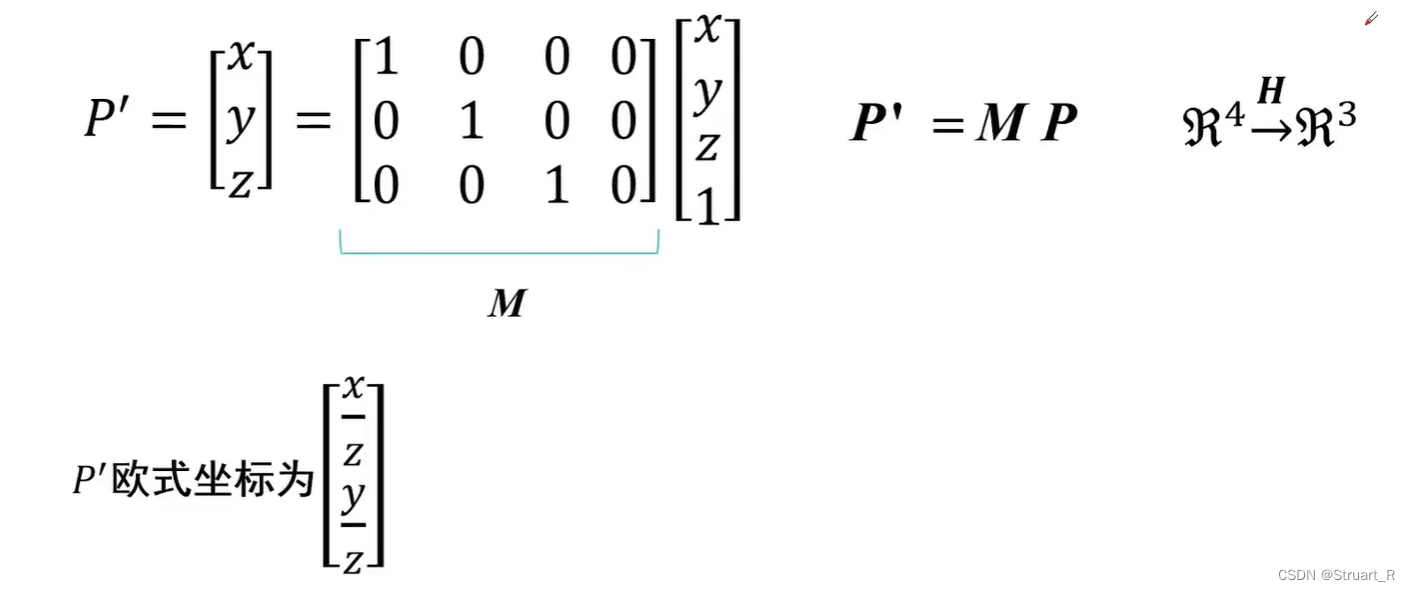
6、世界坐标系下的摄像机模型
假设世界坐标系做一个旋转与平移后转换到摄像机坐标系
,那么存在旋转矩阵R(三行三列),平移矩阵T(三行一列),对于旋转矩阵有三个自由度,平移矩阵有三个自由度,那么外参数总共有六个自由度。
那么此时像素坐标系相对于世界坐标系
的映射如下:
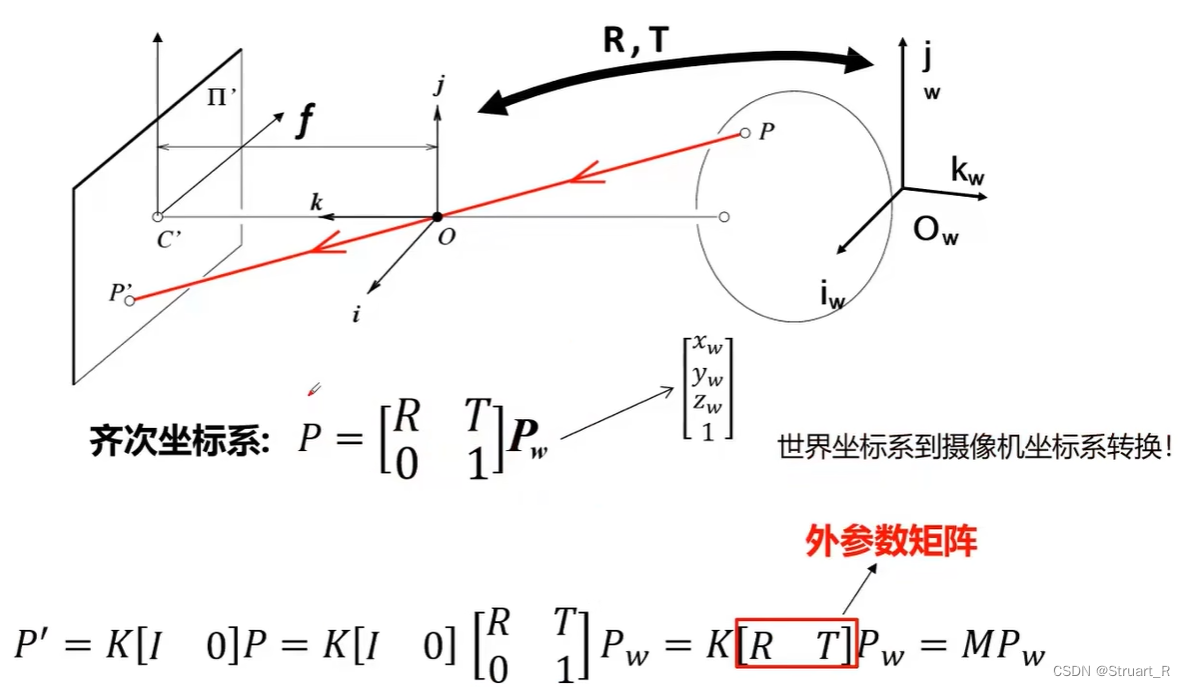
同时考虑外参数和内参数情况下,投影矩阵M有11个自由度。
7、Faugeras定理
Faugeras定理作为三维重建领域的一个重要定理,从多个视角观察二维图像到三维场景的几何关系。
对于Faugeras定理的介绍如下:

8、投影变换的性质
投影变换中存在下面的性质:
(1)点投影为点,线投影为线
(2)近大远小
(3)角度不再保持,平行线相交,3D世界终的平行线相交于“影消点”。

三、其他摄像机模型
1、弱透视投影摄像机
弱透视投影摄像机:假设摄像机到物体的不同区域的距离相同。
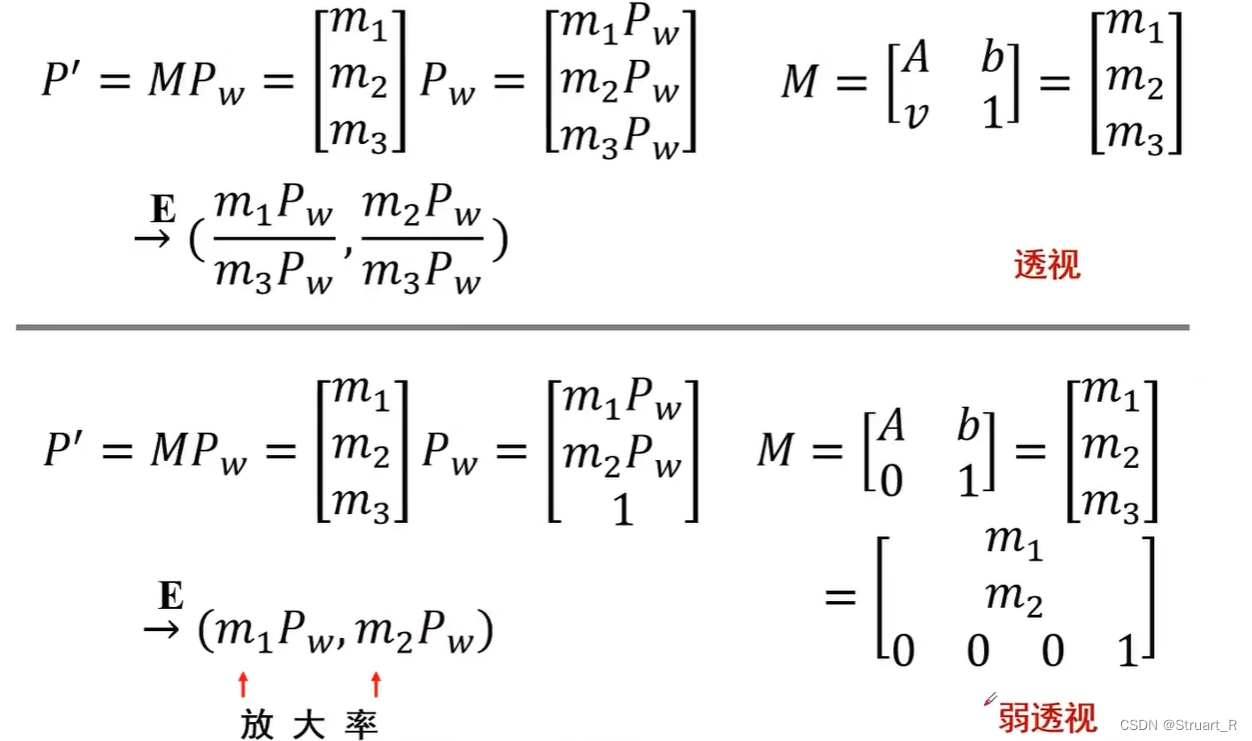
2、正交投影摄像机
正交投影摄像机:摄像机中心到像平面距离无限远,此时z等于∞,变换式如下:



