NeRF的实现过程_nerf全连接网络设计

注：此文章为本人学习NeRF原论文的总结，过程中学习了其他博客的思想，如有可能存在抄袭的情况请联系本人修改，如有错误欢迎指出交流。

NeRF

新视角合成（Novel View Synthesis）：在已知视角下对场景进行一系列的捕获 (包括拍摄到的图像，以及每张图像对应的内外参)，合成新视角下的图像，NeRF 不需要中间三维重建的过程（隐式重建），仅根据相机参数和图像，直接合成新视角下的图像。

NeRF [1]用一个 MLP 表示一个静态场景（隐式重建），输入是空间坐标和观察视角，输出是颜色和体密度，经过体渲染后可以得到新视角的合成图像。

输入：空间中的坐标 $x(x,y,z)$, 相机视角方向 $d(\theta ,\varphi )$

映射：$F_{\Theta }:(x,d)\to (c,\sigma )$，$\Theta$ 是网络的参数

中间输出：颜色 $c(r,g,b)$，体密度 $\sigma$

最终输出：体渲染后得到RGB图像

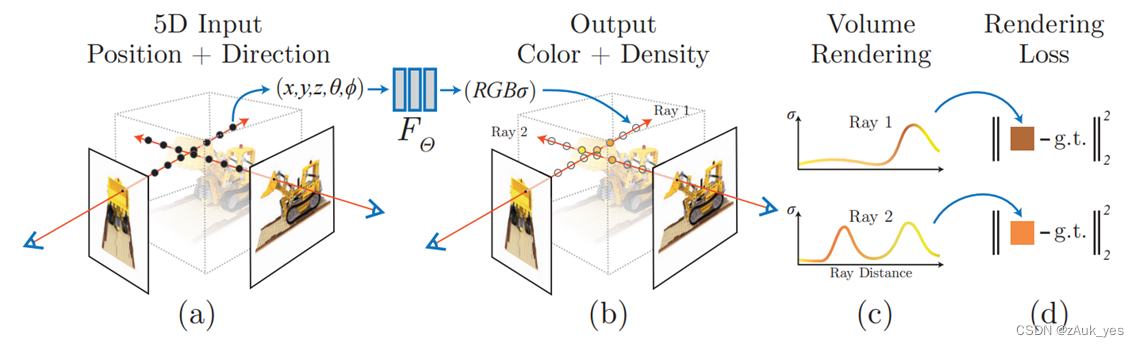
NeRF 的实现过程：（请注意每一步的输入输出，有助于更好地了解整个过程）

第一步：光线的生成

输入：一张RGB图像 输出：图像每个像素的 $o(x,y,z),d(x,y,z)$以及由 $o,d$ 得到的 $x(x,y,z)$

​ 在初看 NeRF 这篇文章时个人觉得有不少地方容易产生误解，因为 NeRF 中强调光线和渲染这些概念，有点难以和空间中的坐标和视角方向这些联系起来，首先要明确的是输入是什么，起到什么作用，输入和光线有什么关系。

​ MLP的输入是一系列空间坐标的点 $x(x,y,z)$，这些点同时具有相机视角（或者说方向）这个属性，这一系列的点可以模拟出一条从相机发射出的光线。光线的生成过程如下：

1.1 坐标系的转换：在进行光线的生成之前，首先需要了解在 NeRF 中一些相关坐标概念：

在NeRF中文件的处理涉及到三种坐标系：

​ 世界坐标系：表示物理上的三维世界坐标

​ 相机坐标系：表示虚拟的三维相机坐标

​ 图像坐标系：表示输入图片的二维坐标

其中不同坐标系下的坐标有以下的转换关系：相机中的坐标${\left[X_c,Y_c,Z_c\right]}^T$和三维世界的坐标$ [X, Y, Z]^T$
[ X c Y c Z c 1 ] = [ r 11 r 12 p 13 t x r 21 r 22 r 23 t y r 31 r 32 r 33 t z 0 0 0 1 ] [ X Y Z 1 ] \left[

$$\begin{array}{l} X_c \\ Y_c \\ Z_c \\ 1 \end{array}$$ \right]=\left[ $$\begin{array}{llll} r_{11} & r_{12} & p_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \\ 0 & 0 & 0 & 1 \end{array}$$ \right]\left[ $$\begin{array}{l} X \\ Y \\ Z \\ 1 \end{array}$$ \right] ⎣⎢⎢⎡​Xc​Yc​Zc​1​⎦⎥⎥⎤​=⎣⎢⎢⎡​r11​r21​r31​0​r12​r22​r32​0​p13​r23​r33​0​tx​ty​tz​1​⎦⎥⎥⎤​⎣⎢⎢⎡​XYZ1​⎦⎥⎥⎤​
等式右边的矩阵是一个仿射变换矩阵，用于从世界坐标转换到相机坐标，而在 NeRF 中会提供其逆矩阵用于从相机坐标转换到统一的世界坐标。而二维图片的坐标 $[x,y{]}^T$ 和相机坐标系的坐标转换关系为：
$$\left[\begin{array}{l}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{l}{X}_c\\ Y_c\\ Z_c\end{array}\right]$$
等式右边的矩阵指相机的内参，包含焦距以及图像中心点的坐标，对于相同的数据集内参矩阵一般是固定的。

有了以上的参数，我们可以对一张图像进行下面的处理：

1. 对一张图片进行二维的像素坐标构建

2. 进行像素坐标到相机坐标的变换（根据相机内参）

3. 进行相机坐标到世界坐标的变换（根据相机外参）

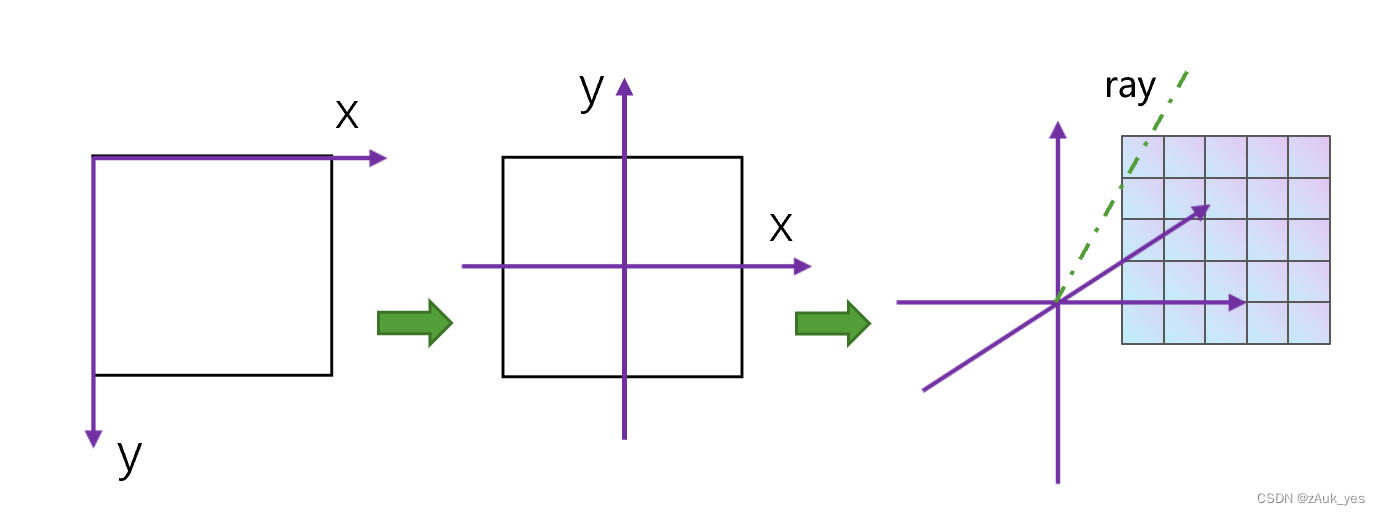
1.2 光线的生成：

通过相机的内外参数，可以将一张图片的像素坐标转换为统一的世界坐标系下的坐标，我们可以确定一个坐标系的原点，而一张图片的每个像素都可以根据原点以及图片像素的位置计算出该像素相对于原点的单位方向向量 $d$（用三维坐标表示，原点也是使用三维坐标表示），根据原点 $o$ 和方向 $d$，改变不同的深度 $t$，就可以通过构建一系列离散的点模拟出一条经过该像素的光线 $r(t)=o+td$。这些点的坐标和方向就是 NeRF 的 MLP 输入，输出经过体渲染得到的值与这条光线经过的像素的值得到 loss。

第二步：位置编码

输入：一条光线上的 $x(x,y,z),d(x,y,z)$ 输出: $\gamma (x),\gamma (d)$

位置编码公式：
$$\gamma (p)=(sin(2^0\pi p),cos(2^0\pi p),...,sin(2^{L-1}\pi p),cos(2^{L-1}\pi p))$$
这里应该关注维度的变化：$R->R^{2L}$，需要注意在上一步提到模拟一条光线时用的是一系列离散的点，那么对应这些点的坐标都是不同的（64个），但单位方向 $d(x,y,z)$ 对于这条光线上的点来说都是相同的，对每一个点进行位置编码，原来是 3 维，L 取 10，那么最终的维度就是 3×2×10=60 维，同理单位方向向量维度也是 3，L 取 4，最终是 24 维，这就是论文中 MLP 网络上提到的 $\gamma (x)60$ 和 $\gamma (d)24$

第三步：MLP 预测

输入：$\gamma (x),\gamma (d)$ 输出： $c(r,g,b),\sigma$

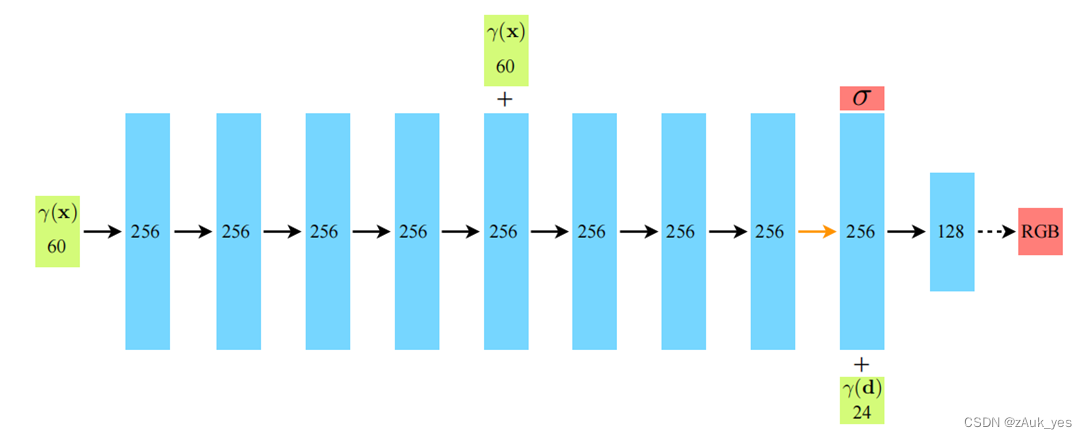
MLP 结构较为简单，这里不多做叙述，但需要注意的是，我们提到用一系列的点模拟一条光线，一条光线穿过一个像素，也就是说对一条光线上的每个点，都需要经过一次MLP，在文中提到一条光线粗采样64 个点那么这 64 个点都会经过MLP，也就是会输出 64 个 $\sigma$ ，然后再加入 $\gamma (d)$ ，注意对这 64 个点来说它们都是处在同一条光线上，所以每个点的 $\gamma (d)$ 都是一样的，然后得到 64 个点对应预测的 rgb 值。

第四步：体渲染

输入：一条光线上的 $c(r,g,b),\sigma$ 输出：渲染后的 RGB 值

在传统的体渲染方法[2]中，通过吸收发射模型进行光强的计算：
$$I(D)=I_{0}T(D)+{\int }_0^{D}g(s)T^{{}^{\prime }}(s)ds$$
其中 $T^{{}^{\prime }}(s)=exp(-{\int }_s^D\tau (x)dx)$，这一项被称为透明度，吸收发射模型等式第一项表示来自背景的光，乘以空间的透明度，这一部分表示光照经过介质后被吸收剩下的光强，第二项是源项 g（s)（表示介质通过外部照明的发射或反射增加的光）乘以位置 s 到眼睛位置 D 的透明度（即 $T^{{}^{\prime }}(s)$）在每个位置 s 贡献的积分（注意这个思想，我们使用一系列的点模拟一条光线，那么每个点都有它的属性）。在 NeRF 中吸收发射模型等式第一项视作背景光，忽略不计，通过坐标换算之后得到：

​ $$I(0)={\int }_0^{\infty }g(s)T^{\prime }(0,s)ds={\int }_0^{\infty }{T}^{\prime }(0,t)\tau (t)c(t)dt$$，

​ 其中 $T^{\prime }(0,t)=exp(-{\int }_0^t\tau (x)dx)$

那么 $\sigma (r(t))$ 可以表示在这条射线上，$t$ 位置的体积密度（也就是体密度，预测出来的 $\sigma$），$c(r(t),d)$ 就可以表示在这条射线上，$t$ 位置 $d$ 方向的光强。再考虑到不是每个位置上都有介质，取了介质的边界平面 $t_n,t_f$，最终得到论文中的公式：
$$\begin{gathered} C(r)={\int }_{t_n}^{t_f}T(t)\sigma (r(t))c(r(t),d)dt \\ \int T(t)=exp(-{\int }_{t^n}^t\sigma (r(s))ds),r(t)=o+td \end{gathered}$$
由于没有办法对连续对每个点进行采样得到积分值，因此引入了它的离散形式，把区间进行划分再进行采样：
$$C(r)=\sum _{i=1}^N{T}_i(1-exp(-{\sigma }_i{\delta }_i))c_i,where{T}_i=exp(-\sum _{j=1}^{i-1}{\sigma }_i{\delta }_i)$$
其中 $$t_i\sim U[t_n+\frac{i-1}{N}(t_f-t_n),t_n+\frac{i}{N}(t_f-t_n)],{\delta }_i=t_{i+1}-t_i$$，在这里对离散化的公式作一个解释，$T_i，c_i$ 都是和连续积分公式中采用一致的形式，即透明度和光强，而 $1-exp(-{\sigma }_i{\delta }_i)$ 则来源于Max 的体渲染论文[2]，$\sigma$ 的含义为体密度，也被称为不透明度或消光系数，实际上不透明度的定义为$\alpha =1-T(s)=1-exp(-{\int }_0^s\tau (t)dt$)（即1 - 透明度）当划分的区间足够小时，可以得到$\alpha =1-exp(-\tau s)$，其中 $s=\delta ,\tau =\sigma$。

除此以外，对于离散化的体渲染公式还有另一种理解，注意到在这个吸收发射模型中我们一直用的是光强C 这个概念，实际上我们人眼看到的是颜色 C，在此处个人也有一些疑惑关于两者的联系，但在这个模型中我们可以认为光强 C 进入人眼所看到的是颜色（作一个这样的理解，从人眼或者说相机出发一条光线经过一段具有某种透明度的物体后击中了某个不透明的物体，这个物体的不透明度 $\alpha$，也就是光线终止在这点的概率，那么眼睛“看到”的就是该物体的颜色 C，也因此可以认为透明度是光线穿过这点的概率，不透明度是在这点击中粒子终止的概率）如果将 C 表示为颜色，那么论文中离散化的体渲染公式我们可以得到以下的理解：
$$\begin{gathered} C(r)=\sum _{i=1}^N{T}_i\alpha c_i, \\ {T}_i=exp(-\sum _{j=1}^{i-1}{\sigma }_i{\delta }_i), \\ \alpha =(1-exp(-{\sigma }_i{\delta }_i)) \end{gathered}$$
alpha blending 在计算机图形学中用于不同透明度的图像合成，对于具有颜色 $c_f$ 不透明度为 $\alpha$ 的前景， 与颜色为 $c_b$ 的背景合成后的颜色为：
$$c=\alpha c_f+(1-\alpha )c_b$$
这反映了前景和后景对成像点颜色的贡献，取两个极端值，假设 $\alpha$ 的值为1，即不透明度为1，完全不透明，那么最终成像点的颜色就完全取决于前景的颜色，后景的颜色对成像无贡献，$\alpha$ 为0，不透明度为0，即完全透明，那么前景的颜色对最终成像的颜色没有贡献。在体渲染公式中，同样可以这样理解，在公式 $\alpha =(1-exp(-\sigma_i\delta_i)) $ 中，体密度 $\delta =0$，则 $\alpha =0$，即当体密度为0时，不透明度为0，完全透明，也就是这一段不存在物体，对最终成像的颜色也就没有贡献 。体渲染的离散求积公式可以表述为以下形式：
C ^ = c 1 α 1 + c 2 α 2 ( 1 − α 1 ) + c 3 α 3 ( 1 − α 1 ) ( 1 − α 2 ) + . . + c n α n ( 1 − α 1 ) ( 1 − α 2 ) … ( 1 − α n − 1 )

$$\begin{aligned} \hat{\mathbf{C}}=& \mathbf{c}_1 \alpha_1 \\ &+\mathbf{c}_2 \alpha_2\left(1-\alpha_1\right) \\ &+\mathbf{c}_3 \alpha_3\left(1-\alpha_1\right)\left(1-\alpha_2\right) \\ &+. . \\ &+\mathbf{c}_n \alpha_n\left(1-\alpha_1\right)\left(1-\alpha_2\right) \ldots\left(1-\alpha_{n-1}\right) \end{aligned}$$ C^=​c1​α1​+c2​α2​(1−α1​)+c3​α3​(1−α1​)(1−α2​)+..+cn​αn​(1−α1​)(1−α2​)…(1−αn−1​)​
$T_i=exp(-{\sum }_{j=1}^{i-1}{\sigma }_i{\delta }_i)$ 表示前 i-1 个位置累积的透明度，${\alpha }_i$ 表示第 i 个位置的不透明度，$c_i$ 是第 i 个采样点预测出来的颜色，最终成像点的颜色就是根据每个点的颜色贡献（不透明度）的叠加（这里个人觉得和体渲染的思想是一致的，每个点贡献对应的积分），MLP 实现的功能就是预测每个点的 $c$ 和 $\sigma$。这其实也解释了为什么颜色的预测值输出与视角方向有关（view-dependent），在不同的视角观察物体，对于同一个物体其在空间中的位置是固定的，也就是体密度只与位置有关系（采样点的坐标已经统一到世界坐标系下），而不同的视角代表着不同的光线，当（光线）方向改变时，成像的颜色值取决于经过这条光线上的物体，而不同光线经过的物体显然是不一致的。

至此就是 NeRF 的前向过程。

优化方式

1.使用位置编码后为何网络能学习到高频信息，这篇论文[3]进行了分析，

2.分层次采样：根据上面对体渲染公式的分析，我们可以得知为了更好地进行隐式重建表示物体，应该在体密度高的地方进行更多的采样，因此在 coarse 网络中预测 $N_c$ 个点的体密度值时构建概率密度函数，其中权值$w_i=T_i(1-exp(-{\sigma }_i{\delta }_i)),\widehat{w_i}=w_i/{\sum }_{j=1}^{N_c}{w}_j$ 就表示了在这些地方不透明度高，即更有可能存在物体，根据 PDF 进行逆变换采样得到新的 $N_f=128$ 个点，再使用 $N_c+N_f$ 输入到 fine 网络中。（注：这里计算 loss 时有两类，即$N_c$ 作为输入得到的预测值经过渲染的输出，以及$N_c+N_f$ 输入时得到的预测值经过渲染的输出。）

[1] Mildenhall B, Srinivasan P P, Tancik M, et al. Nerf: Representing scenes as neural radiance fields for view synthesis[J]. Communications of the ACM, 2021, 65(1): 99-106.

[2] Max N. Optical models for direct volume rendering[J]. IEEE Transactions on Visualization and Computer Graphics, 1995, 1(2): 99-108.

ACM, 2021, 65(1): 99-106.

[2] Max N. Optical models for direct volume rendering[J]. IEEE Transactions on Visualization and Computer Graphics, 1995, 1(2): 99-108.

[3] Tancik M, Srinivasan P, Mildenhall B, et al. Fourier features let networks learn high frequency functions in low dimensional domains[J]. Advances in Neural Information Processing Systems, 2020, 33: 7537-7547.