LSTM长短期记忆网

 笔记来源——

【重温经典】大白话讲解LSTM长短期记忆网络 如何缓解梯度消失，手把手公式推导反向传播

 

LSTM网络结构

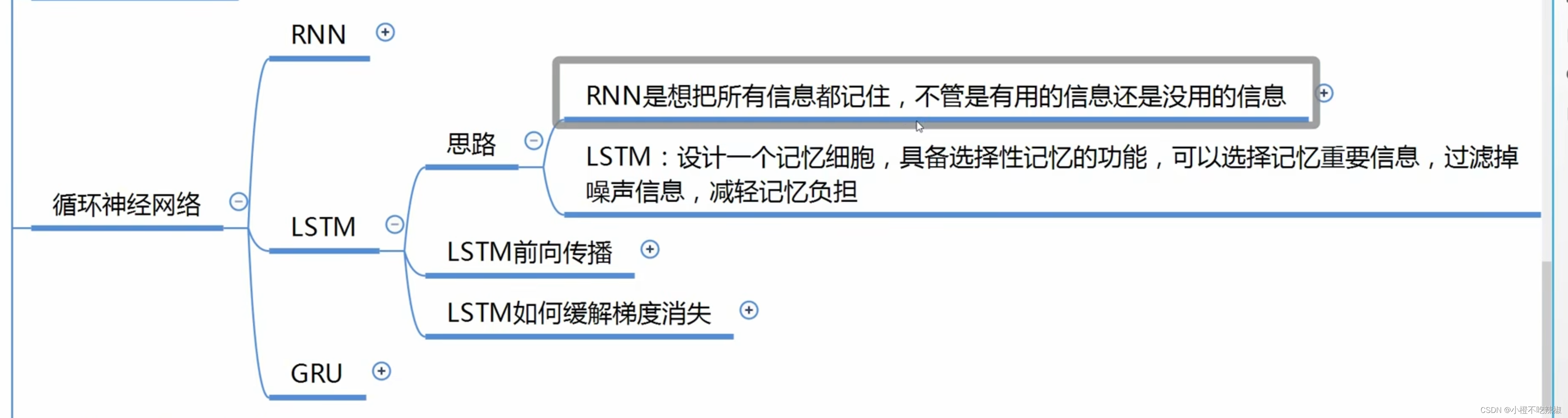
RNN结构

下面拉出一个单元结构进行讲解

：记忆细胞，t-1时刻的记忆细胞

:表示状态,t-1时刻的状态

正是这样经过了一个单元，我们输出了新的的状态跟记忆细胞

：门单元  

:forget,遗忘门

:更新门

:输出门

公式推导

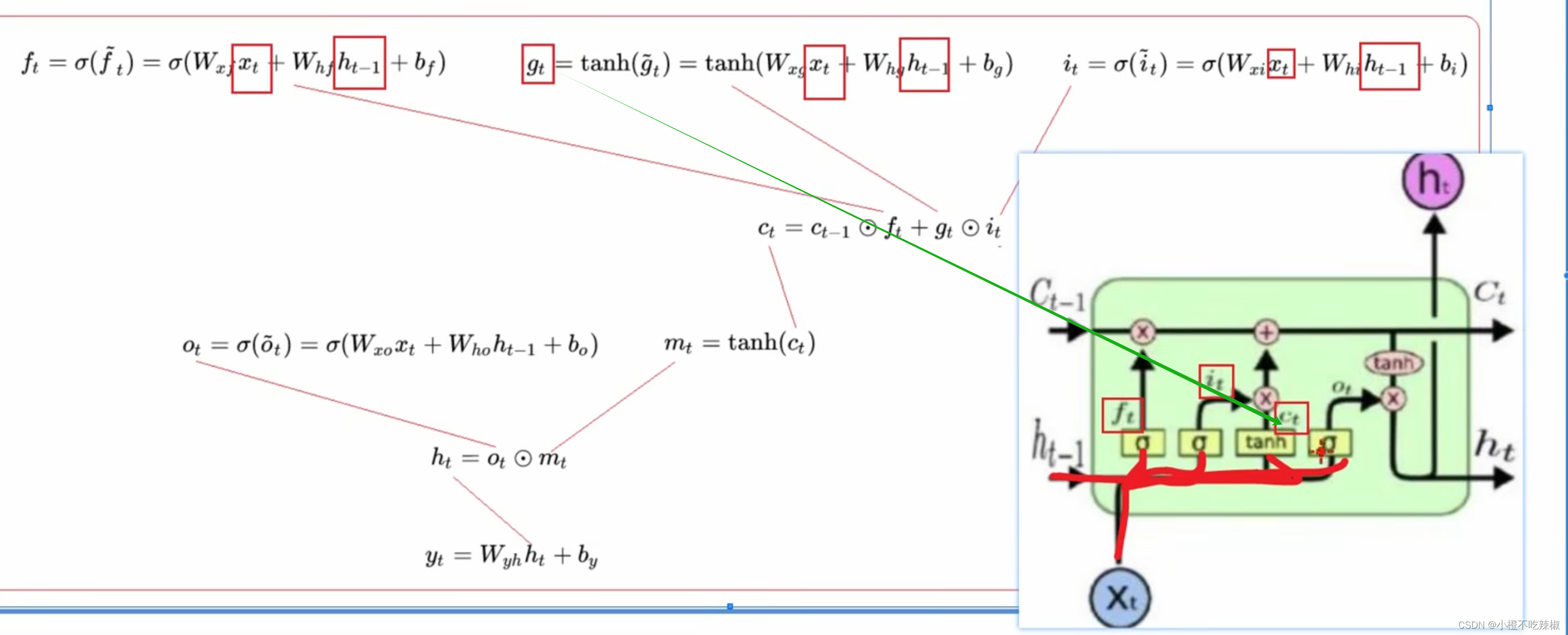
这里的小就认为是我们的

结构讲解

通过例子我们来理解一下

假设我们要考试，左边的时间部A是我们的高等数学，中间的时间部是我们的线性代数

假设我们要去考线性代数，就相当于我们要去复习我们的线性代数，打个比方就是我们已经翻开了线性代数的课本以及习题开始复习。中间那些条条就相当于我们复习形成的记忆。最后上面的就是我们要去考试，就是我们考试的一个分数。复习当中会形成我们新的记忆，会带着我们复习好的记忆拿去考试。最后下面的就是我们考完试的这样的一个状态。

之后就好理解了，前一科，我们要去考高等数学，那么就是我们考完高等数学的这样一个记忆。就是我们复习完之后所形成的跟高数有关的一些记忆。左下脚的就是考完高数的这样一个状态。

然后我们就有一个目标，我们希望考完的每一个得分都有好的一个目标/成绩（上面的），因为我们这里是一个有监督学习，我们需要有一个好的成绩来监督我们每一个参数的迭代更新。

遗忘门

假设我们的脑容量是有限的，我们在考完高等数学之后需要遗忘其相关内容给我们的线性代数留空间。

刚刚我们了解到我们需要去复习我们的线性代数，第二步就是我们需要把线性代数没有关的内容遗忘掉，所以就是遗忘掉我们过去积累下来的一些记忆。

如何操作？

我们知道里面有所有的数都是介于0-1，例如[0，1，1，0，1],就是一个向量，通过跟这样的一个向量相乘，他就会把向量里面对应的位置的一些记忆的内容给调整，是0就遗忘，是1就调整。

更新门

注：这里的小就是之前说的

这里作用的对象就是，这里的就相当于我们形成的新的记忆，但是这个新的记忆并不是全都有用，所以我们这里要有一个门要去选择性的提取。所以这里的就是可以过滤掉没有用的记忆。

然后到这里就形成了我们新的记忆

这里的就很容易理解了，这里的就跟我们过去的记忆和当下生成的记忆有关系，将他们相加结合起来。

tanh是激活函数

输出门

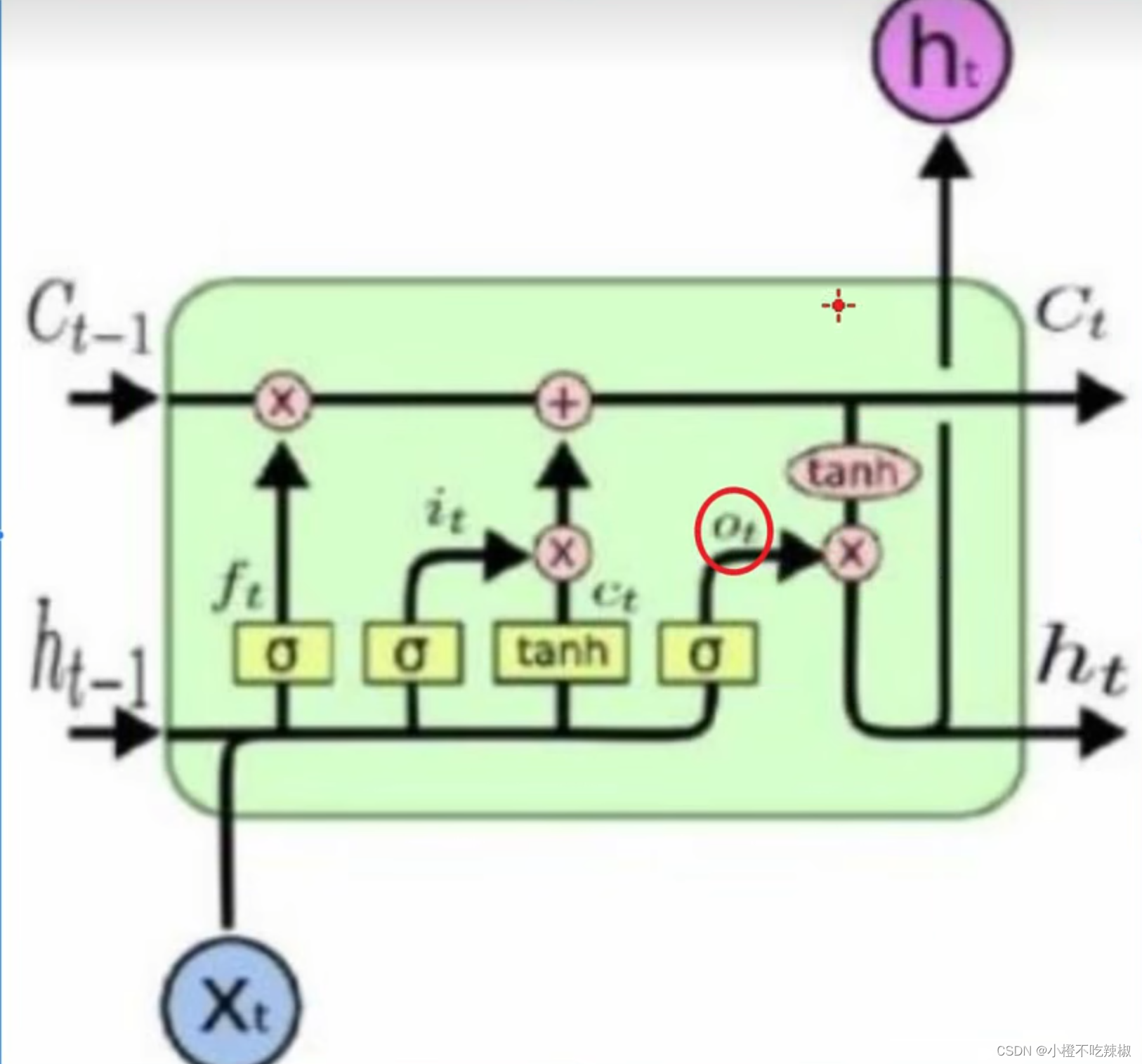
这里分红色的tanh如何理解？

可以理解为：它可以将我们记忆的内容转化为答题的能力

因为我们复习到的东西很多很全面，最后我们考试的时候不可能将所有复习到的东西都考一遍，有可能只考到其中的一部分，所以我们这里的的作用就是我们只需要用到其中的一部分的知识来进行答题。

RNN梯度消失回顾

什么是RNN？

RNN是递归神经网络（Recurrent Neural Network）的缩写。它是一种神经网络结构，专门用于处理序列数据，具有记忆和顺序处理的能力。

在传统的前馈神经网络中，每个输入与输出之间都是独立的，而RNN通过引入循环连接，允许信息在网络中传递并保持状态。

RNN的基本结构包括：

1. 循环连接（Recurrent Connections）：RNN中的每个时间步都有一个循环连接，使得网络可以在处理当前输入时考虑之前的信息。这种连接使得RNN能够处理任意长度的序列输入。

2. 隐藏状态（Hidden State）：在RNN的每个时间步，网络都会产生一个隐藏状态，用于存储之前时间步的信息。隐藏状态是RNN的记忆，使得网络能够在处理序列时保持上下文信息。

3. 时间步（Time Steps）：RNN处理序列数据时，会将输入序列分割成多个时间步。在每个时间步，网络接收一个输入，并生成一个输出和一个隐藏状态，然后将隐藏状态传递到下一个时间步。

4. 递归单元（Recurrent Units）：RNN中的递归单元通常采用LSTM（Long Short-Term Memory）单元或GRU（Gated Recurrent Unit）单元等结构，以解决传统RNN中的梯度消失和梯度爆炸等问题。

RNN在自然语言处理（如语言建模、机器翻译、情感分析）、时间序列分析（如股票预测、天气预测）和序列生成（如文本生成、音乐生成）等领域都有广泛的应用。

对于RNN梯度消失的这个问题，可以参考我这篇笔记

RNN循环神经网络及其梯度消失笔记

LSTM如何缓解梯度消失

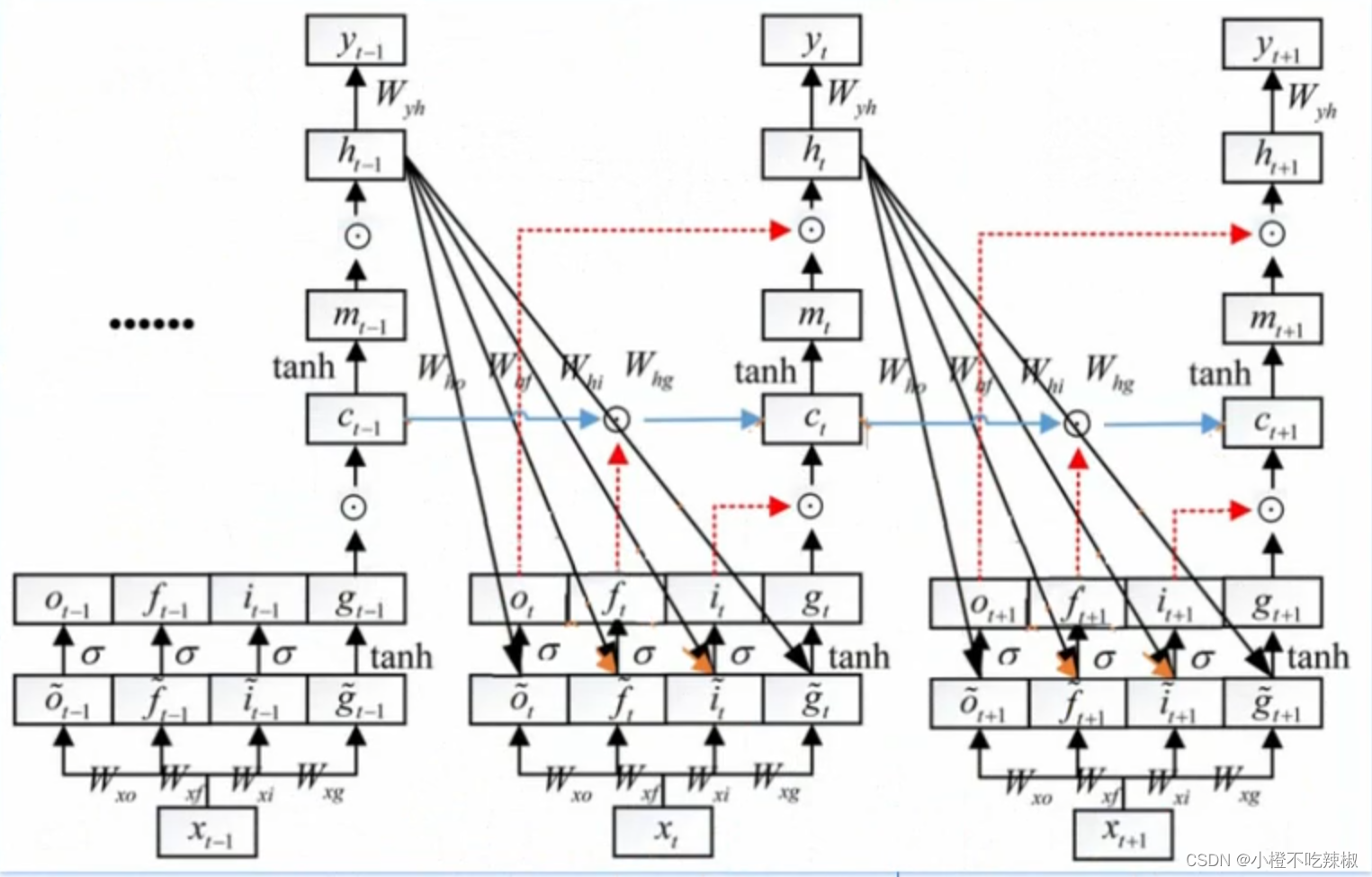
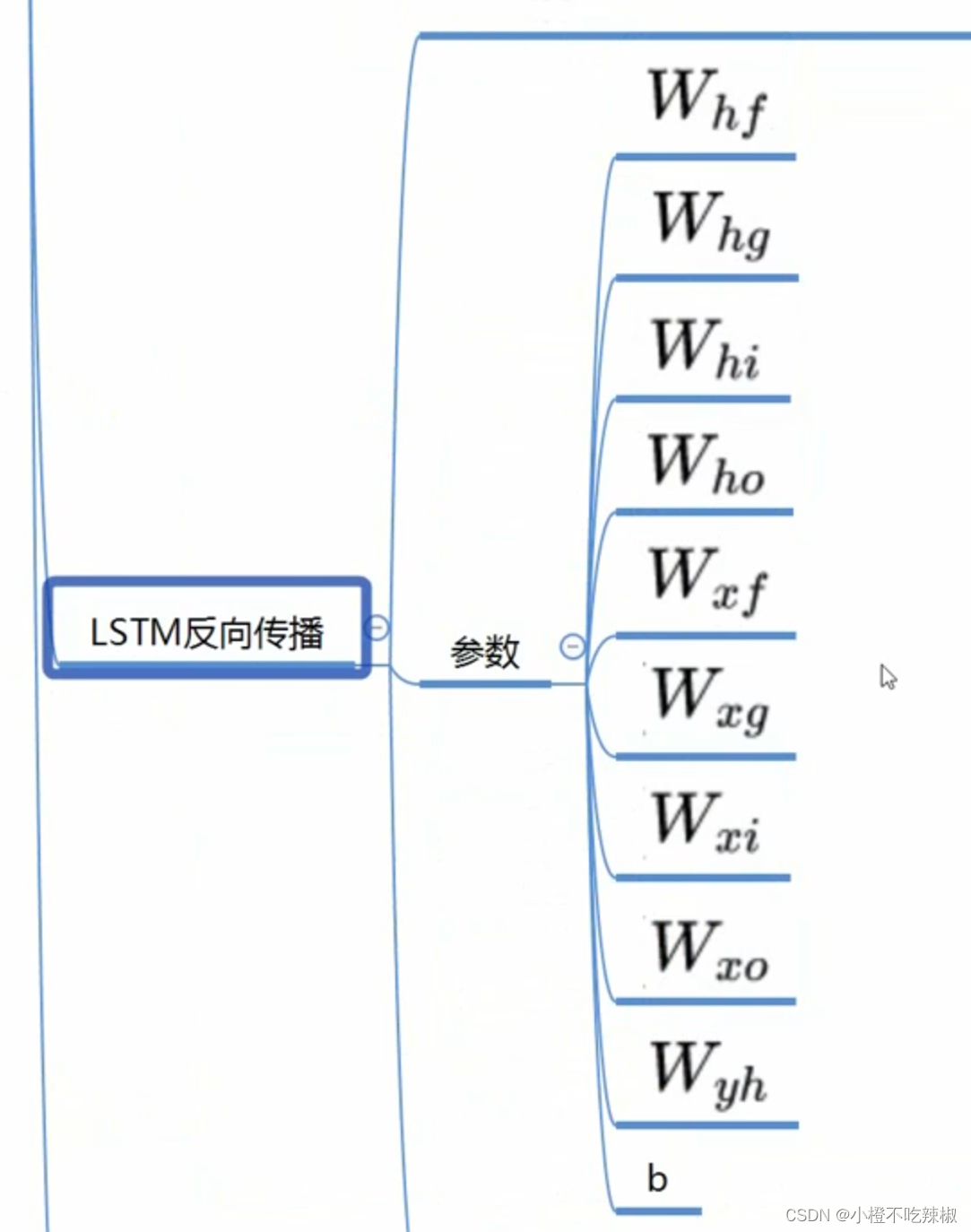
可以看到我们的参数是非常多的

我们以参数为例，推导一下我们反向传播的过程

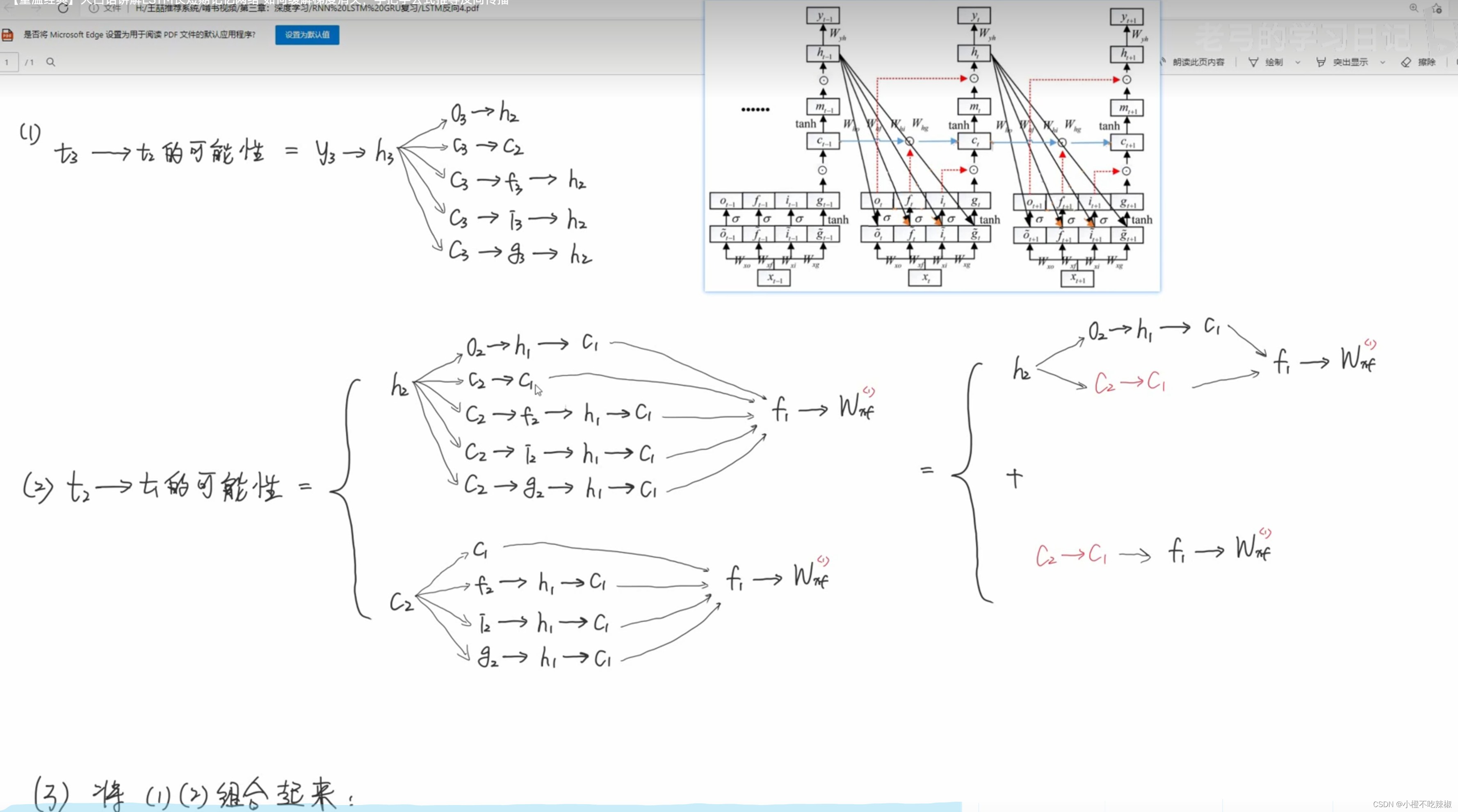
假设我们最右边就是t=3,中间t=2,最前面t=1

对三个位置的分别求导

这是我们求导的路径

不同路线的求偏导

简化方程

下面就是我们简化后的方程

由于要求第三个，但路径是非常多的，就没有写推导的方程了，就写了一下路径

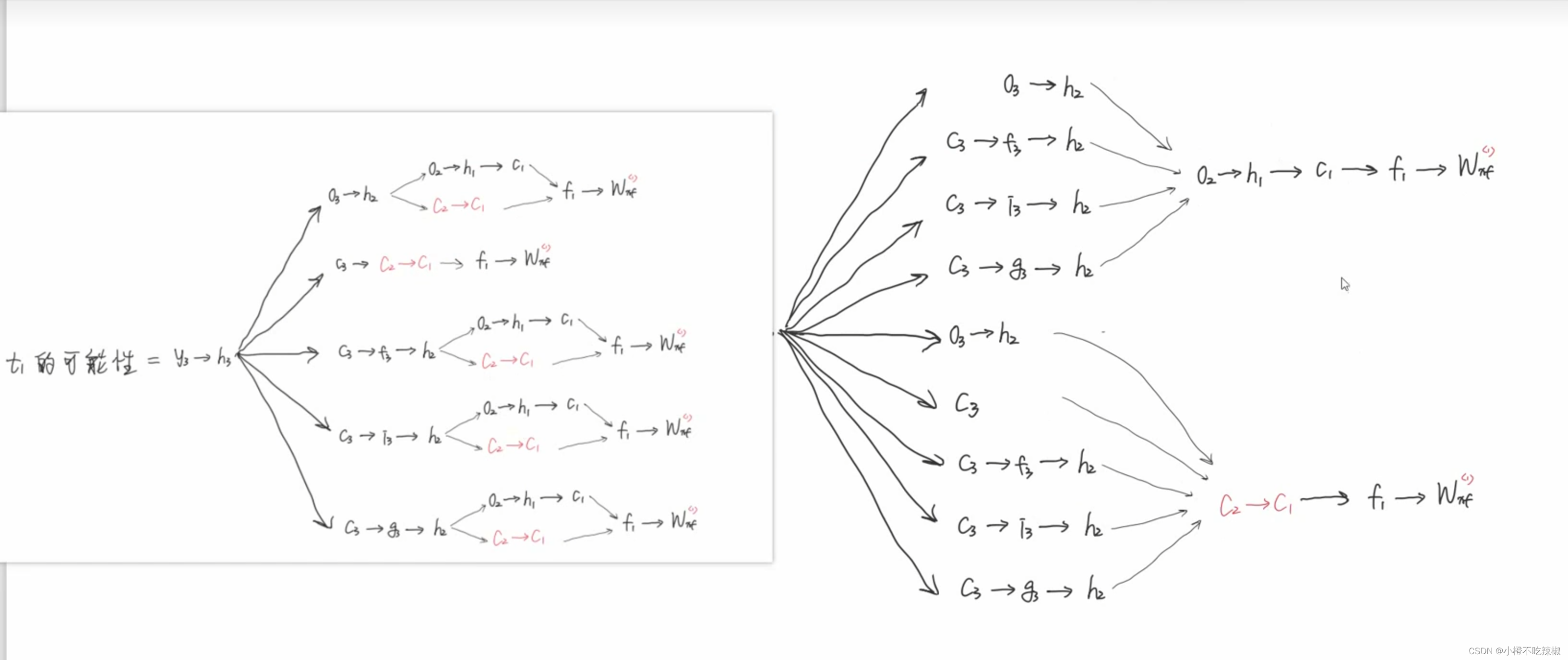
合并一下同类项，并将这两个路径组合

把上面的这个路径简化为下面那样

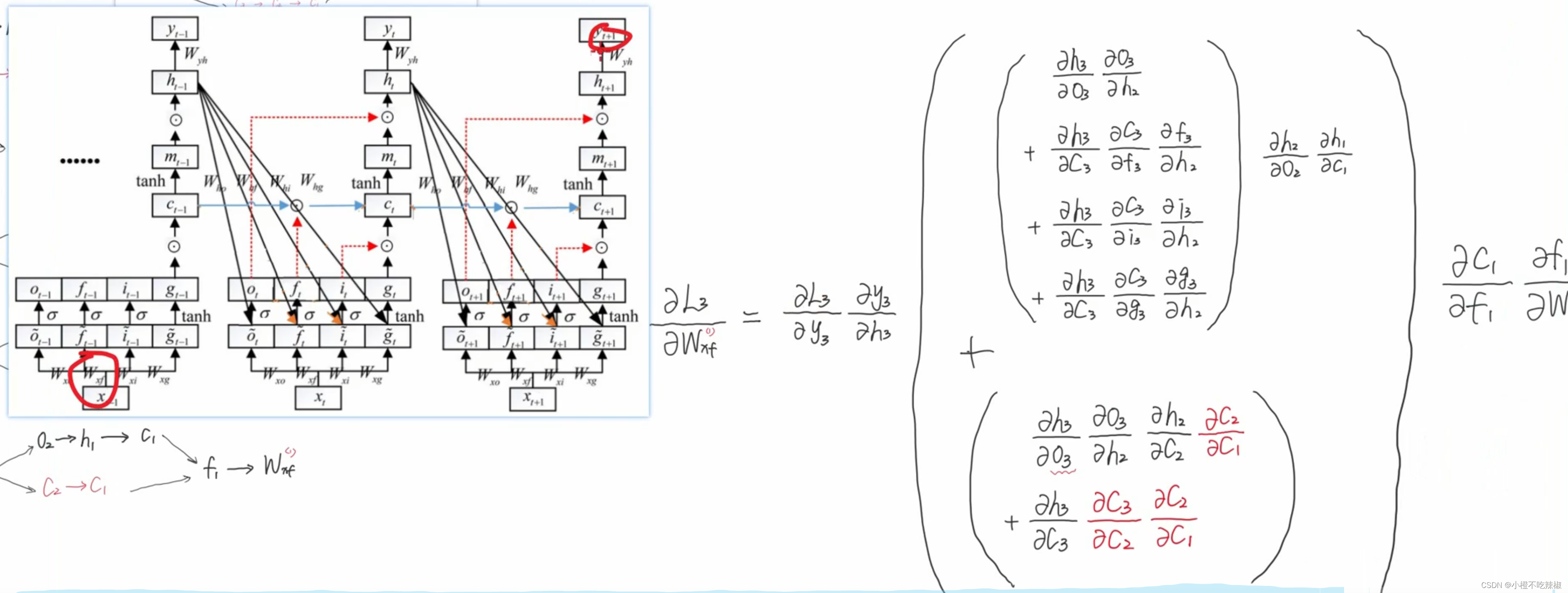
我们继续把从到的路继续简化

再表达为右边的公式

最后得到的就是右边的这些，而且我们发现了连乘项的出现，然后我们针对这个部分对其求一下

这个式子有一个特点，就是他是由4个部分进行相加的

这些参数是可以去调控他值的一个大小的，也就是说我们的模型可以通过学习去控制它值的一个大小的。从而去控制的值的大小的。也就是说我可以去控制这些参数而去使得处于比较接近于一个1的数。

我们可以知道，当我们的时间跨度越长的时候 ，我们的路径越长，中间的累乘项也会更多，这个部分就容易带来我们的梯度消失的可能，所以这个部分我们没有办法去把控。

但是这里我们的连乘项，可以灵活的去调控它的参数，去实现很多1*1*1的效果，就导致连乘的效果大大的削弱了，梯度消失的可能性就大大的降低了，所以就极大的缓解了梯度消失的可能性。