- 1Android源码编译失败,没有具体错误信息_out/soong/.bootstrap/bin/soong_build out/soong/bui
- 2Android Studio导入项目 下载gradle很慢或连接超时_download gradle
- 3uniapp 安卓 plus调用原生文件选择
- 4爬取拉钩Java招聘数据
- 5在阿里云平台部署ChatGLM2-6B模型、langchain-ChatGLM2知识库_langchain-chatchat 阿里云人工只能平台
- 6Gradle多渠道打包(动态设定App名称,应用图标,替换常量,更改包名,变更渠道)方法一_java动态打包app名称
- 7「软技能|真・复盘」学习类复盘:迭代出自己的高效学习法_学什么可以让自己的技术不断迭代
- 8低代码与数字化工具:重塑软件开发的新范式
- 9leetcode题解:矩阵置零_输入一个n*n的矩阵,然后将其右上半部分的元素置零。 输入 第一行输入n,然后输入n*
- 10stable diffusion插件controlnet的详细讲解以及用法说明_stable diffusion controlnet
【Matlab群体智能算法第四期】基于Tent混沌映射、自适应t分布和动态选择策略的TDPSO算法(含完整matlab代码)_t分布raodong
赞
踩
0.前言
上一篇文章主要对基于Tent混沌映射的改进粒子群算法原理及matlab代码进行讲解,并将改进后粒子群算法的寻优能力进行测试。
该篇文章基于上述改进方向的基础上,针对群体智能算法中的种群更新迭代部分进行改进讲解,本次主要介绍基于Tent混沌映射、自适应t分布和动态选择策略的改进粒子群优化算法。Tent混沌映射原理及matlab代码见上期,链接如下:https://blog.csdn.net/hbdlhy/article/details/134151702?spm=1001.2014.3001.5502
1.自适应t分布策略原理及matlab代码
采用自适应t分布算法能够对种群粒子的位置进行扰动,提高算法的收敛速度。同时,将算法迭代次数iter作为自适应t分布的自由度参数,这使得算法在迭代前期具有较好的全局开发能力,在迭代后期具有良好的局部探索能力,极大的提高了算法的收敛速度及求解效率。自适应t分布策略粒子位置更新方式如下:
式中:为自适应t分布扰动后种群位置,
为种群i在第t次迭代式的位置,t(iter)为以种群迭代次数为自由度参数的自适应t分布函数。
采用上述公式进行自适应t分布对种群位置扰动更新后,既充分利用了当前位置信息,又增加了随机干扰信息,有利于算法跳出局部最优.而随着迭代次数的增加,t分布逐渐向高斯分布靠拢,有利于增强算法的收敛速度。
基于上述理论,自适应t分布策略的matlab代码如下所示:
- function best_x=mult_t_random(x,df,Lb,Ub,p)
- %x为扰动前种群粒子的位置
- %df为t分布的自由度参数
- %Lb为种群位置下限
- %Ub为种群位置上限
- %P为动态选择概率
- %自适应t分布变异
- if rand > p
- x_tb = x + x.*trnd(df); %基于迭代次数的t分布变异
- %边界处理
- x_tb(x_tb>Ub) = Ub(x_tb>Ub);
- x_tb(x_tb<Lb) = Lb(x_tb<Lb);
- %粒子位置选择
- fitvalue_old = fitness_obl(x);
- fitvalue_tb = fitness_obl(x_tb);
- if fitvalue_tb <fitvalue_old
- best_x = x_tb;
- else
- best_x = x;
- end
- else
- best_x=x;
- end
-
- % %粒子边界约束检查
- I=best_x<Lb;
- best_x(I)=Lb(I);
- U=best_x>Ub;
- best_x(U)=Ub(U);
- end
2.动态选择概率原理及matlab代码
采用上述自适应t分布变异算子,能够很大程度上提升算法的寻优性能,但是若无差别的对每次迭代中的所有个体使用,一方面会增加算法的计算时间,另一方面不利于发挥原算法本身的特点。针对这一现象,动态选择概率p能够调节自适应t分布变异算子的使用,减缓该现象对算法寻优能力的影响,动态选择概率策略具体公式如下:
式中:maxiter为最大 迭代次数,iter为当前迭代次数,决定了动态选择概率的上限,
决定了动态选择概率的变化幅度,通过查阅相关文献,当
、
时,调节作用最优。
动态选择概率p使得算法在迭代前期有较大概率利用自适应t分布变异算子对种群的位置进行扰动,改善原算法在迭代初期就存在收敛于最优解得倾向;同时在迭代后期,充分发挥原算法良好的局部开发能力,并以较小概率的t分布变异作为补充,提升算法的收敛速度。
基于上述原理及公式,matlab代码如下:
- %% 动态选择策略
- %w1=0.5;%动态选择概率的上限
- %w2=0.1;%动态选择概率的变化幅度
- %MaxDT为最大迭代次数
- %iter为算法当前迭代次数
- p=w1-w2*(MaxDT-iter)/MaxDT;%自适应t分布变异算子
3.基于Tent混沌映射、自适应t分布和动态选择策略的改进粒子群优化算法
结合上述种群初始化及更新位置改进策略,基于Tent混沌映射、自适应t分布和动态选择策略的改进粒子群优化算法matlab代码如下:
- %% 基于Tent混沌映射、自适应t分布和动态选择策略的改进粒子群优化算法主程序
- clc;
- clear all;
- close all
- %% 算法基本参数设置
- c1=2; %学习因子1
- c2=2;%学习因子2
- w=0.7;%惯性权重
- MaxDT=500;%最大迭代次数
- D=3;%搜索空间维数(未知数个数)
- N=30;%初始化群体个体数目
- Lb=[-100,-100,-100];%种群解的下限
- Ub=[100,100,100];%种群解的上限
- Vmax=[1,1,1];%速度上限
- Vmin=[-1,-1,-1];%速度下限
- w1=0.5;%动态选择概率的上限
- w2=0.1;%动态选择概率的变化幅度
- a=0.5;%Tent混沌系数,0~1之间
- Best_f=[];pop=[];
- %% 基于Tent混沌映射的种群初始化
- for L=1:N
- pop(L,:) = Tent_int(D,a,Lb,Ub);
- Best_f(1,L)=fitness_obl(pop(L,:));
- end
- V=rand(N,D);
- %计算各个粒子的适应度值并初始化Pi和Pg
- [fitnessgbest bestindex]=min(Best_f);
- gbest=pop(bestindex,:);
- pbest=pop;
- fitnesspbest=Best_f;
-
- %% 粒子群算法更新迭代部分
- for iter=1:MaxDT
- %动态选择策略
- p=w1-w2*(MaxDT-iter)/MaxDT;%自适应t分布变异算子
- %进入种群更新
- for j=1:N
- %种群更新
- V(j,:)=w*V(j,:)+c1*rand*(pbest(j,:)-pop(j,:))+c2*rand*(gbest-pop(j,:));
- %更新速度边界检查
- I=V(j,:)<Vmin;
- V(j,I)=Vmin(I);
- U=V(j,:)>Vmax;
- V(j,U)=Vmax(U);
- pop(j,:)=pop(j,:)+V(j,:);
- %基于自适应t分布变异策略位置更新
- pop(j,:)=mult_t_random(pop(j,:),iter,Lb,Ub,p);
- %粒子边界检查
- PI=pop(j,:)<Lb;
- pop(j,PI)=Lb(PI);
- PU=pop(j,:)>Ub;
- pop(j,PU)=Ub(PU);
- %计算更新后种群的适应度函数值
- Best_f(j)=fitness_obl(pop(j,:));
-
- %个体极值更新
- if Best_f(j)<fitnesspbest(j)
- pbest(j,:)=pop(j,:);
- fitnesspbest(j)=Best_f(j);
- end
-
- %全局极值更新
- if Best_f(j)<fitnessgbest
- gbest=pop(j,:);
- fitnessgbest=Best_f(j);
- end
-
- end
- %记录粒子全局最优解
- Fgbest(iter)=fitnessgbest;
-
- end
- %% 结果可视化
- figure
- plot(Fgbest)
- title(['适应度曲线 ' '终止次数=' num2str(MaxDT)]);
- xlabel('进化代数');
- ylabel('适应度')
- end
基于上述matlab代码,利用测试函数fitness_obl,进行算法性能对比,测试函数代码如下:
- function f=fitness_obl(x)
-
- f=sum((x+0.5).^2);
4.改进PSO算法性能对比
通过第3节中目标函数,结合前三期PSO算法求解效率进行对比,通过对上述目标函数进行多次对比,记录各算法目标函数的最大值、最小值及均值。改进后的TDPSO算法适应度曲线如下所示:
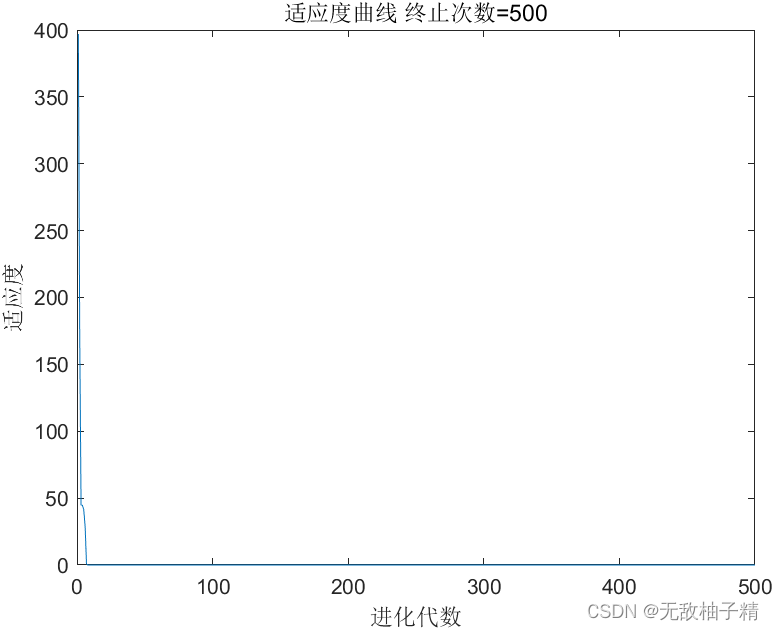
图1 基于Tent混沌映射、自适应t分布和动态选择策略的改进粒子群算法适应度曲线
根据上述结果可以看出,该算法能够在极短的时间内实现最优目标函数值求解,极大的提升了算法的求解速度及求解效率。
为了进一步对比改进后该算法的求解性能,不同改进方向下,算法测试函数的适应度函数值如下:
| 运行次数 | 基于混沌映射与自适应t分布变异的改进PSO | 基于反向学习改进后 | 标准粒子群算法 | 基于Tent映射改进后 |
| 1 | 0 | 3.36E-31 | 0.0831 | 3.71E-29 |
| 2 | 3.08E-33 | 1.82E-29 | 0.0547 | 5.55E-31 |
| 3 | 0 | 1.85E-32 | 0.0294 | 3.24E-28 |
| 4 | 2.47E-32 | 2.74E-29 | 0.0119 | 2.26E-28 |
| 5 | 1.85E-32 | 3.08E-33 | 0.0477 | 1.02E-28 |
| 6 | 0 | 2.28E-29 | 0.0399 | 3.00E-28 |
| 7 | 0 | 7.67E-31 | 0.0459 | 3.73E-29 |
| 8 | 0 | 2.90E-31 | 0.0235 | 8.03E-28 |
| 9 | 2.77E-32 | 1.26E-31 | 0.0043 | 4.35E-29 |
| 10 | 0 | 1.39E-31 | 0.0532 | 8.26E-30 |
| 均值 | 7.39557E-33 | 7.01E-30 | 0.03936 | 1.88215E-28 |
| 最小值 | 0 | 3.08E-33 | 0.0043 | 5.54668E-31 |
| 最大值 | 2.77334E-32 | 2.74E-29 | 0.0831 | 8.03128E-28 |
根据上述结果能够发现,采用自适应t分布和动态选择策略后极大的提升了算法的求解能力及鲁棒性,在同条件运行10次的情况下,基于Tent混沌映射、自适应t分布和动态选择策略的改进粒子群优化算法具有更高的精度及求解效率。
5.结束语
本博客在编写过程中主要参考文献为:
[1]张伟康,刘升.自适应t分布与黄金正弦改进的麻雀搜索算法及其应用[J].微电子学与计算机,2022,39(03):17-24.
感谢大家耐心阅读,本文代码改进部分均为作者自身复现,谢绝转载,严禁以此进行二次售卖,后续更新方向为其余种群初始化改进策略及种群更新策略,及白鲸优化算法原理及相应变体等。
作者主要更新方向为:
(1)智能算法复现及改进;
(2)微电网/综合能源系统容量配置、优化调度等方向
(3)时间序列预测(机器学习、深度学习方向)
欢迎大家相互交流,另作者水平有限,难免存在疏忽之处,若有错误请大家指正,谢谢。
该专题往期博文传送门:
1.【Matlab群体智能算法第一期】粒子群算法及其变体(一)_matlab群运算-CSDN博客


