深度学习理论基础（二）深度神经网络DNN

  神经网络通过学习大量样本的输入与输出特征之间的关系，以拟合出输入与输出之间的方程，学习完成后，只给它输入特征，它便会可以给出输出特征。神经网络可以分为这么几步：准备数据集、划分数据集、搭建网络模型、训练网络、测试网络、使用网络。
  神经网络的训练过程，就是经过很多次前向传播与反向传播的轮回，最终不断调整其内部参数（权重 ω 与偏置 b），以拟合任意复杂函数的过程。内部参数一开始是随机的（如 Xavier 初始值、He 初始值），最终会不断优化到最佳。
  对于整个流程如下：我们先准备好样本数据以及样本对应的标签（一般给模型的输入都是tensor格式的，如果初始数据集不是tensor格式则需要转为tensor格式），将整个样本分为训练集和测试集，一般为8/2或7/3，训练集必须大于测试集，因为我们是训练模型，所以要使用更多的数据去训练优化模型，具体的划分比例按实际情况分析。 训练过程：先定义损失函数、学习率和优化器（具体选择哪个函数和优化器根据情况而定）。将训练集的样本放入网络中去获得预测标签，然后将预测的标签和真实样本的标签放入损失函数中进行计算损失，再将计算的损失进行反向传播，并使用优化器进行优化模型参数。训练优化模型的参数。 测试过程：测试过程和训练过程唯一的区别就是测试网络中不需要回传梯度，即不需要进行反向传播。所以也不需要定义损失函数和优化器，直接将测试集的样本放入模型进行一次前向传播，得出预测标签，然后将预测标签和真实标签进行比较，最终得出准确率。
  神经网络：深度神经网络（DNN）、卷积神经网络（CNN）。

一、基础知识点

Ⅰ 参数部分

1. 损失函数：计算真实值和预测值差异的一类函数。预测值越接近真实值时，损失越低。我们训练的最终目的就是使得损失函数降到最低。一般用在训练网络中，将样本放入模型中得出预测标签，然后将预测标签和真实标签放入损失函数中计算损失，再将损失进行回传（反向传播），通过优化器进行优化模型的参数。损失函数有很多种，可用于不同的神经网络模型。

2. 激活函数：引入非线性性，使得神经网络能够学习复杂的模式和函数。激活函数通常被应用在神经网络的每一层的输出上。选择合适的激活函数通常取决于具体的任务和数据集。如果每层网络输出后不加上激活函数进行非线性调整的话，那么就算搭建一百层的网络，其实一层就可以搞定。所以激活函数是很必要的！神经网络各层功能函数详情查看地址。
   
   

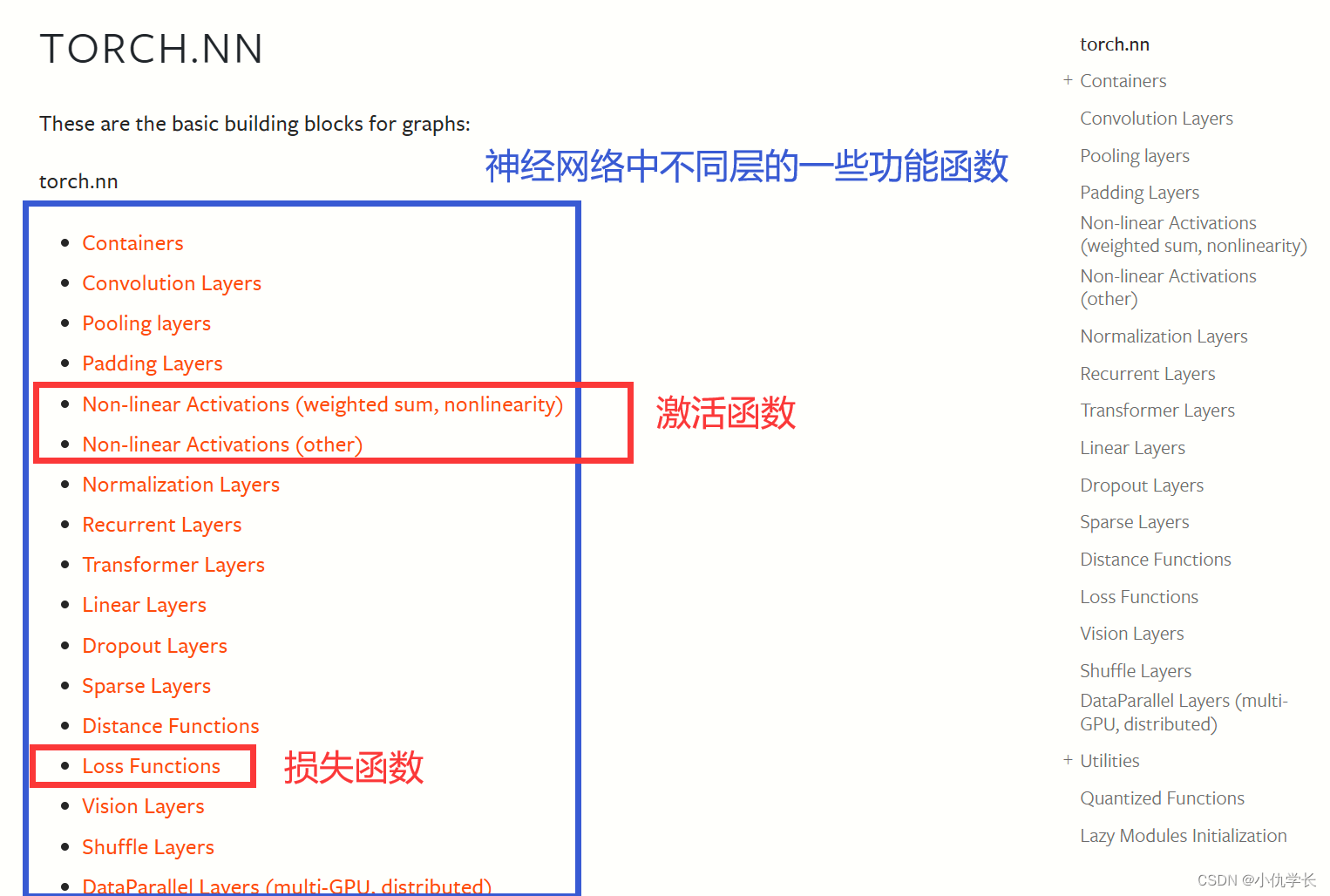
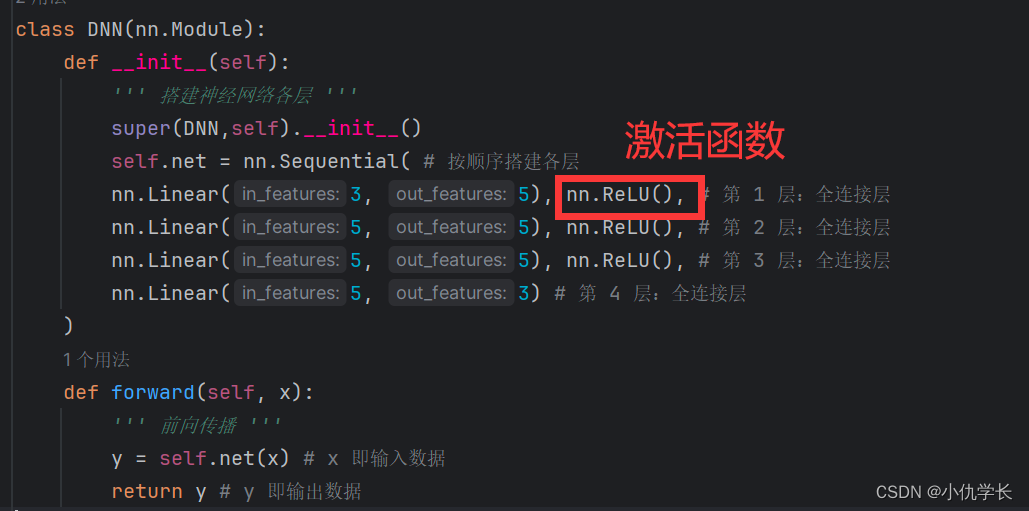
3. 学习率：训练神经网络时的一个关键超参数，它控制模型参数在每次迭代中更新的幅度。一个合适的学习率可以使模型在训练过程中快速收敛到局部最优解或全局最优解，而一个不合适的学习率可能会导致训练过程出现问题，例如收敛速度过慢、陷入局部最优解等。

Ⅱ 模型部分

1. 模型的输入：模型的输入通常需要是张量（tensor）的形式。这是因为深度学习模型是基于张量运算构建的，张量提供了一种有效的方式来表示和处理数据。在深度学习模型中使用输入数据，你通常需要将原始数据转换为张量的形式。
2. 训练集和测试集：训练集是用来训练模型的数据集，它包含了模型需要学习的样本和对应的标签。在训练过程中，模型通过训练集中的样本进行学习，调整参数以最小化损失函数。在模型训练完成后，使用测试集来评估模型在未知数据上的泛化能力。测试集的目的是检查模型是否能够正确地推广到新的、未见过的数据上，以验证模型的性能和有效性。
3. 训练网络和测试网络：训练网络和测试网络的区别就在于，训练网络需要回传梯度，即反向传播。而测试网络不需要回传梯度。
4. 前向传播：在前向传播过程中，输入数据通过神经网络的各个层，经过权重和偏置的线性组合，然后通过激活函数得到输出。前向传播的目的是计算模型的预测值（或者说输出值），然后将预测值与实际标签进行比较以计算损失函数。这一过程沿着网络的正向进行，从输入层到输出层。
5. 反向传播 ：反向传播是训练神经网络的关键步骤，它通过计算损失函数关于网络参数（权重和偏置）的梯度，来调整参数使得损失函数减小。反向传播利用链式法则从输出层向输入层计算梯度，将损失沿着网络反向传播。反向传播过程可以分为两个阶段：首先计算损失函数对网络输出的梯度，然后逐层反向传播这些梯度以计算损失函数对各层参数的梯度。计算得到的梯度可以用于更新模型参数，通常使用梯度下降等优化算法进行参数更新。这个过程很复杂，原理不必掌握。我们直接使用函数即可。
6. 梯度下降优化器：
   （1）optim.SGD: 随机梯度下降（Stochastic Gradient Descent），是最基础的优化器之一，通过梯度的方向进行参数的更新。
   （2）optim.Adam: Adam 优化器结合了动量梯度下降和 RMSProp 算法，对学习率进行自适应调整，适用于大多数深度学习任务。
   （3）optim.Adagrad: 自适应梯度算法（Adaptive Gradient Algorithm），根据参数的历史梯度调整学习率。
   （4）optim.RMSprop: RMSProp 优化器使用指数加权移动平均来调整学习率，有效地解决了 AdaGrad 学习率下降过快的问题。
   （5）optim.Adadelta: AdaDelta 优化器也是自适应学习率算法，类似于 RMSProp，但没有学习率超参数。
   （6）optim.AdamW: 在 Adam 优化器的基础上添加了权重衰减（Weight Decay）的选项，用于对权重进行正则化。
   （7）optim.LBFGS: 拟牛顿法的一种，适用于较小的数据集和参数较少的情况。
     这些优化器类提供了不同的优化算法和超参数选项，可以根据具体任务的需求选择合适的优化器来进行模型训练。
7. batch_size: 每次训练投入模型的样本个数。
8. epochs：全部样本训练的轮次。1 个 epoch 就是指全部样本进行 1 次前向传播与反向传播。

二、深度神经网络模型搭建

以该神经网络框架为例：

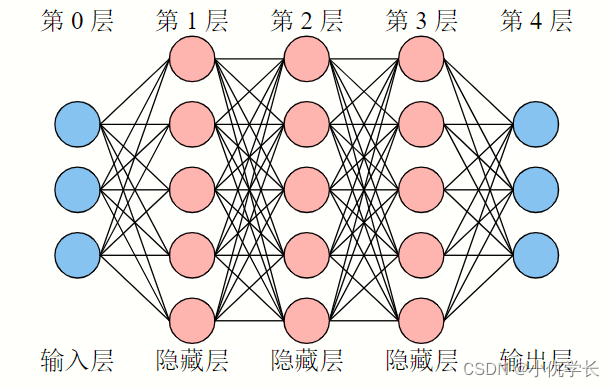
1. 准备数据集

  无论是任何模型，第一步都是先要准备好进行训练的数据集。为了演示，我们这里自己通过代码生成数据集。如上述模块框架，输入特征x个数为3，输出特征y个数也为3。

"""随机生成10000行1列的输入数据。使用torch.rand生成的数据已经是tensor格式了"""
	X1 = torch.rand(10000, 1)  # 输入特征 1
    X2 = torch.rand(10000, 1)  # 输入特征 2
    X3 = torch.rand(10000, 1)  # 输入特征 3
    
"""将输入特征的各行逐行相加，并与1比较。<1为1，否则为0."""    
    Y1 = ((X1 + X2 + X3) < 1).float()  # 输出特征1。
    Y2 = ((1 < (X1 + X2 + X3)) & ((X1 + X2 + X3) < 2)).float()  # 输出特征2。
    Y3 = ((X1 + X2 + X3) > 2).float()  # 输出特征3。
    
"""整合数据集，合并为10000行6列的数据列表"""    
"""axis=1,在第二个维度上合并数据，也就是列的维度上。axis=0，则在行的维度上合并，合并后为60000行1列"""
    Data = torch.cat([X1, X2, X3, Y1, Y2, Y3], axis=1) 
    
1
2
3
4
5
6
7
8
9
10
11
12
13
14

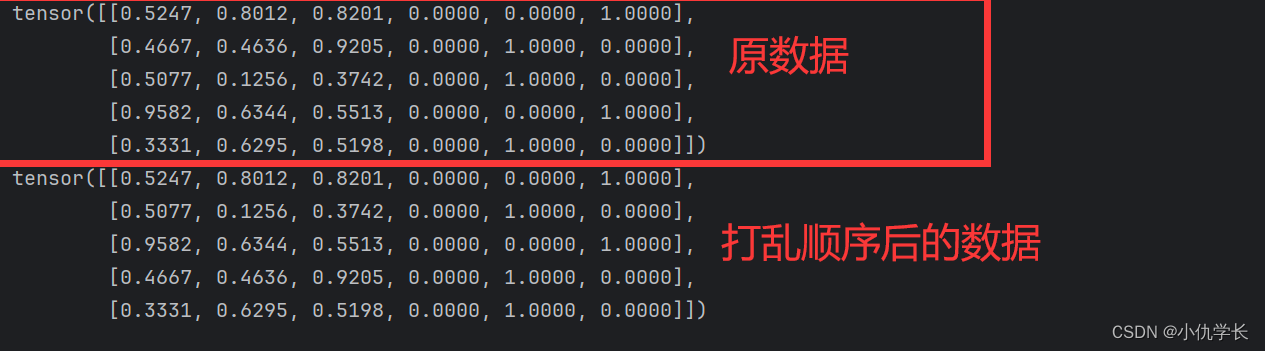
2. 划分数据集

将数据集进行划分，划分为训练集和测试集。下面代码中包含列表的切片操作，详情查看这里。

"""传入参数为：总数据集"""
def train_test_split(Data):
    train_size = int(len(Data) * 0.7)  # 训练集的样本数量
    test_size = len(Data) - train_size  # 测试集的样本数量
    
    """ Data.size(0) 为数据的行数，Data.size(1)的列数 """
    """ Data[第一个维度，第二个维度] ，' : '表示该维度全要 """
    Data = Data[ torch.randperm(Data.size(0)),  :]  # 按行进行打乱样本的顺序，第二个维度不变
    train_Data = Data[: train_size, :]  # 训练集样本
    test_Data = Data[train_size: , :]  # 测试集样本
    return train_Data,test_Data
    
train_Data,test_Data=train_test_split(Data)
1
2
3
4
5
6
7
8
9
10
11
12
13

3. 搭建模型

  搭建神经网络时，以 nn.Module 作为父类，我们自己的神经网络可直接继承父类的方法与属性，nn.Module 中包含网络各个层的定义。每个模型都必须包含forward（前向传播）方法。
  不同模型可以查看模型的框图进行搭建。

class DNN(nn.Module):
    def __init__(self):
        ''' 搭建神经网络各层 '''
        super(DNN,self).__init__()
        self.net = nn.Sequential( 			# 按顺序搭建各层,每一个隐藏层后都使用了 RuLU 激活函数
	        nn.Linear(3, 5), nn.ReLU(), 	# 第 1 层：全连接层
	        nn.Linear(5, 5), nn.ReLU(), 	# 第 2 层：全连接层
	        nn.Linear(5, 5), nn.ReLU(), 	# 第 3 层：全连接层
	        nn.Linear(5, 3)				    # 第 4 层：全连接层
    	)
    def forward(self, x):
        ''' 前向传播 '''
        y = self.net(x) # x 即输入数据
        return y # y 即输出数据
        
model = DNN().to('cuda:0')  #创建子类的实例，并搬到 GPU 上
"""model = DNN()    #在cpu上"""
print(model)                #查看该实例的各层
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

查看模型层数情况：

print(model)                #查看该实例的各层
1

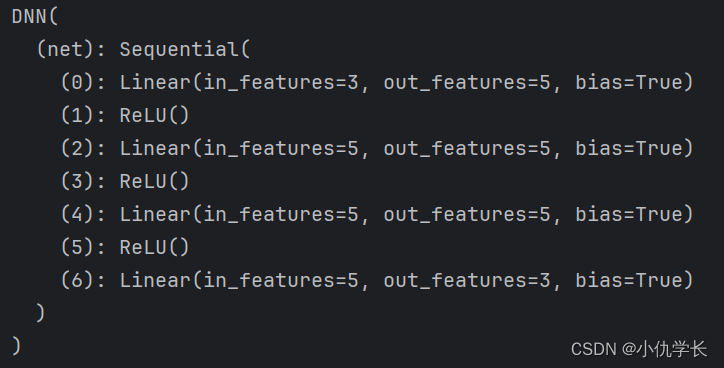
4. 训练网络

def train_net():
    loss_fn = nn.MSELoss() """选择损失函数"""
    learning_rate = 0.01   """设置学习率"""
    
     """定义优化器"""
    """ torch.optim.SGD 是 PyTorch 提供的 SGD 优化器类，用于实现随机梯度下降算法。"""
	"""	model.parameters() 是一个迭代器，它会返回模型中所有需要训练的参数。"""
	"""	lr=learning_rate 设置了学习率（learning rate），即 SGD 算法中用于控制参数更新步长的超参数。""" 
    optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate) 
    
    """ 训练网络"""
    epochs = 1000   
    losses = []           #记录损失函数变化的列表
    
    """给训练集划分输入与输出"""
    X = train_Data[:, :3]     #前3列为输入特征
    Y = train_Data[:, -3:]    #后3列为输出特征
    
    for epoch in range(epochs):
    """前向传播写法一："""
        Pred = model.forward(X)  # 一次前向传播（批量）,获得预测值
    """前向传播写法二：这是因为torch中对模型输入时，自动调用forward方法，不需要显示调用forward方法"""
    """ Pred = model(X)  """
        
        loss = loss_fn(Pred, Y)  # 将预测值和真实值传入损失函数，计算损失。
        losses.append(loss.item())  # 记录损失函数的变化
        optimizer.zero_grad()  # 清理上一轮滞留的梯度
        loss.backward()  # 将损失进行一次反向传播
        optimizer.step()  # 优化内部参数
        print('Epoch [{}/{}], Loss: {:.4f}'.format(epoch + 1, epochs, loss.item()))
        
    """对loss损失进行画图"""    
    Fig = plt.figure()
    plt.plot(range(epochs), losses)
    plt.ylabel('loss'), plt.xlabel('epoch')
    plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

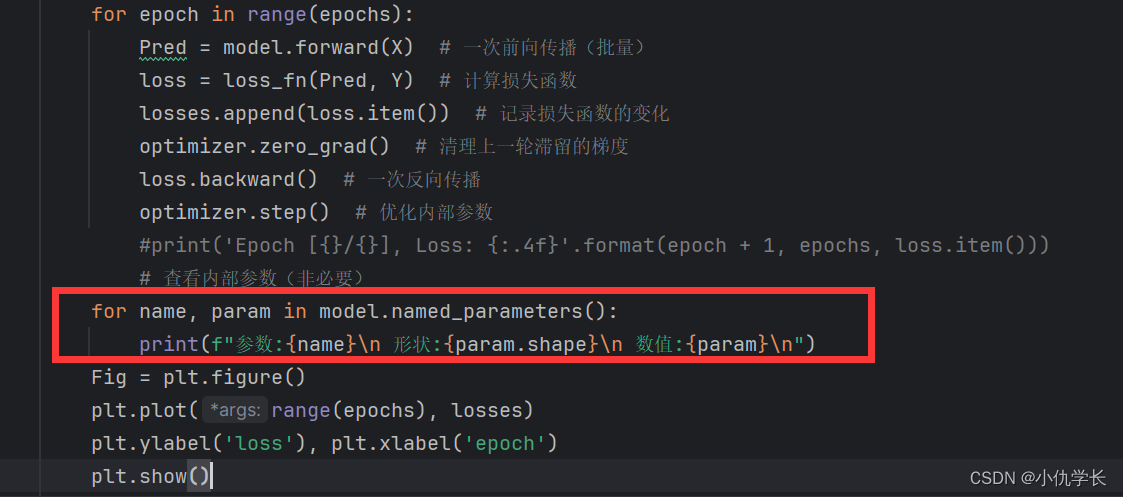
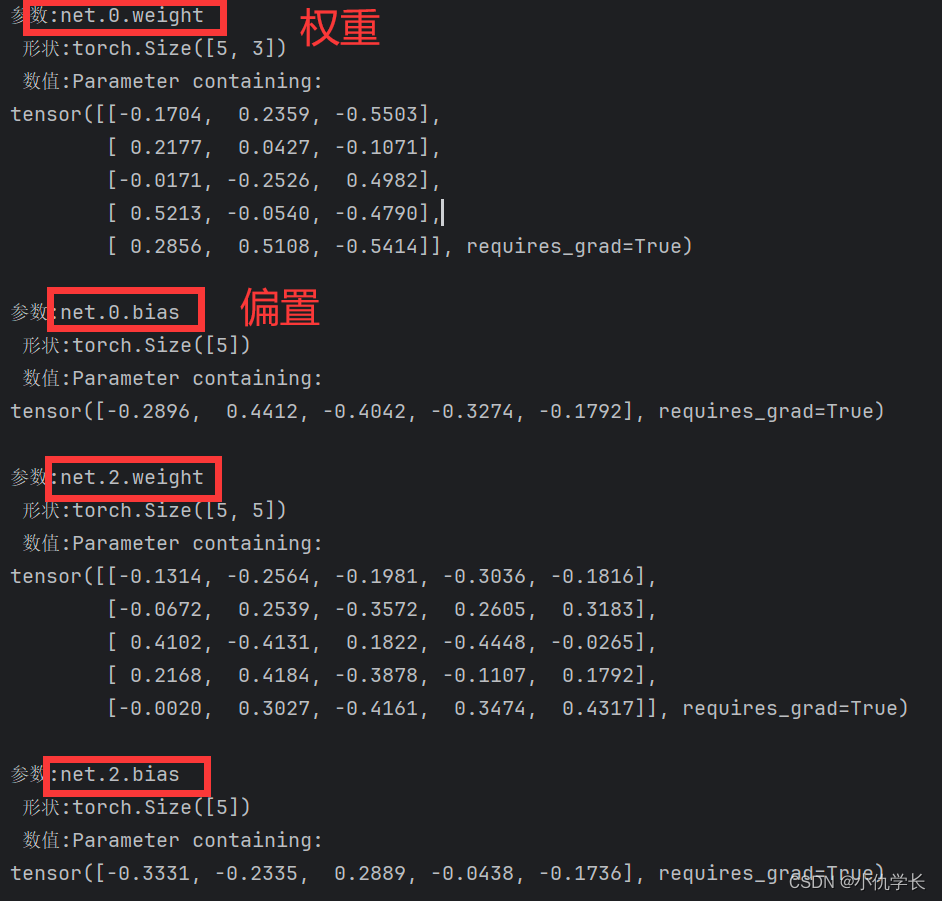
查看模型内部参数

 for name, param in model.named_parameters():
        print(f"参数:{name}\n 形状:{param.shape}\n 数值:{param}\n")
1
2

5. 测试网络

  在测试网络时，通常不需要定义损失函数和优化器。在测试阶段，我们主要关注模型在新的、未见过的数据上的性能表现，而不是在训练集上的表现。因此，不需要对模型进行参数更新，也就不需要定义优化器。

def test_net():
    """给测试集划分输入与输出"""
    X = test_Data[:, :3]     #前3列为输入特征
    Y = test_Data[:, -3:]    #后3列为输出特征
    
    with torch.no_grad():     """该局部关闭梯度计算功能"""
        Pred = model(X)     #一次前向传播（批量）,获得预测值
        
        """torch.argmax(Pred, axis=1) 返回每行中最大值的索引，然后使用这些索引来将对应位置的值设置为1，其他位置的值保持不变。"""
	    Pred[:, torch.argmax(Pred, axis=1)] = 1
	    Pred[Pred != 1] = 0
	    correct = torch.sum((Pred == Y).all(1))  # 预测正确的样本
	    total = Y.size(0)        #全部的样本数量
	    print(f'测试集精准度: {100 * correct / total} %')

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

6. 保存与导入模型

（1）保存和导入整个模型
  通常用于在 PyTorch 中保存训练好的模型。当你在训练神经网络模型时，可能会花费很多时间和计算资源。为了避免每次使用模型时都重新训练，你可以使用 torch.save() 将模型保存到磁盘上，以便稍后加载和使用。比如将模型部署到生产环境或与其他人共享模型。
  模型文件通常以.pth或.pt为后缀。

"""保存已经训练好的模型文件"""    
old_model=DNN()
train_net()  """在保存模型文件前要先训练模型"""
torch.save(old_model, 'old_model.pth')


"""新模型加载已经训练好的模型文件,不需要进行实例化模型""" 
new_model = torch.load('old_model.pth')
test_net()   #测试网络中前向传播的模型要改为new_model。
1
2
3
4
5
6
7
8
9

（2）只保存模型参数文件 (推荐使用，更加轻量化)
  可将保存的模型数据导入新的网络中使用。

"""只保存模型参数"""
old_model=DNN()
train_net()  """在保存模型文件前要先训练模型"""
torch.save(old_model.state_dict(), 'old_model_params.pth')


"""将加载的参数状态字典加载到模型实例new_model中"""
new_model=DNN()
model_state_dict = torch.load('old_model_params.pth')
new_model.load_state_dict(model_state_dict)
test_net()   #测试网络中前向传播的模型要改为new_model。
1
2
3
4
5
6
7
8
9
10
11

（3）导入模型到测试网络
  模型导入后可以直接去跑测试集。因为保存的模型里面各类参数已经训练好，所以不需要再训练。
new_model使用了原有模型文件，我们就需要在测试网络的前向传播中的模型修改为new_model去进行测试。如下：
<1> 导入整个模型

""" 假设原模型已经被保存为： 'old_model.pth' """

def test_net():
    """给测试集划分输入与输出"""
    X = test_Data[:, :3]     #前3列为输入特征
    Y = test_Data[:, -3:]    #后3列为输出特征
    
    with torch.no_grad():  # 该局部关闭梯度计算功能
        Pred = new_model(X)  # 一次前向传播（批量），获得预测值
        
        """使用 torch.argmax() 获取每行最大值的索引，并根据索引设置对应位置的值为 1"""
        Pred_onehot = torch.zeros_like(Pred)
        Pred_onehot.scatter_(1, torch.argmax(Pred, dim=1).unsqueeze(1), 1)
        
        # 将非最大值位置的值设置为 0
        Pred = Pred_onehot
        
        # 计算预测正确的样本数量
        correct = torch.sum(torch.all(Pred == Y, dim=1))
        total = Y.size(0)  # 全部的样本数量
        print(f'测试集精准度: {100 * correct / total} %')

	    
if __name__ == '__main__':
    new_model = torch.load('old_model.pth')
    test_net()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

<2> 导入模型参数

""" 假设原模型已经被保存为： 'old_model_params.pth' """

def test_net():
    """给测试集划分输入与输出"""
    X = test_Data[:, :3]     #前3列为输入特征
    Y = test_Data[:, -3:]    #后3列为输出特征
    
    with torch.no_grad():  # 该局部关闭梯度计算功能
        Pred = new_model(X)  # 一次前向传播（批量），获得预测值
        
        """使用 torch.argmax() 获取每行最大值的索引，并根据索引设置对应位置的值为 1"""
        Pred_onehot = torch.zeros_like(Pred)
        Pred_onehot.scatter_(1, torch.argmax(Pred, dim=1).unsqueeze(1), 1)
        
        # 将非最大值位置的值设置为 0
        Pred = Pred_onehot
        
        # 计算预测正确的样本数量
        correct = torch.sum(torch.all(Pred == Y, dim=1))
        total = Y.size(0)  # 全部的样本数量
        print(f'测试集精准度: {100 * correct / total} %')

	    
if __name__ == '__main__':
    new_model=DNN()
    model_state_dict = torch.load('old_model_params.pth')
    new_model.load_state_dict(model_state_dict)  #新模型加载保存好的模型参数
    
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28