反向传播算法 ( BackPropagation,BP)
PS:需要掌握高等数学中的链式求导法则、偏导数、梯度概念。有一定的神经网络基础知识。
- 反向传播简介
- 反向传播原理及实现
- 总结
一、反向传播简介
BP算法是神经网络用于更新权值的算法,可以说是能让神经网络开始“学习”的核心,所以理解这个算法是非常重要的。本着实践是检验是否理解的唯一标准的原则,我借用了另一位博主的博客代码,稍微修改了一些地方,最后分析算法的结果。原贴在这里http://www.cnblogs.com/charlotte77/p/5629865.html
我们先来理解前向传播是什么。简单说就是:设定一个包含输入层,隐含层,输出层的神经网络,其中权重w和偏置b随意设置一个值,输入一组数据,经过若干神经元计算后产生一个输出,至于输出结果对不对不重要,整个过程本身称之为前向传播。就如同你对一函数f(x)=sin(x)输入了x=1得到f=0.01745一样,不过是f(x)换成了神经网络(一个不知道具体函数表达式的函数)而已。很好理解。
那么反向传播是什么?当你完成一个前向传播后,得到的输出值可能并不是你想要的,你期望得到0.01745但你只得到了0.2,这有0.18255的误差!首先可以确定的是,我们可以通过调整神经网络中的权重w和偏置b来使得误差降低,那么如何调整呢?BP算法把最后的总误差分解,按照一定的权重分配给每一个参数(w和b),而分配原则由总误差对参数求导得到的偏导数来确定,通过高等数学里面的链式求导,我们可以求出每个参数的偏导数,我们来看看具体是怎么实现的。
一、反向传播原理及实现
假如你有这样一个网络,其中i1、i2是输入层,h1、h2、b1为中间层,o1、o2、b2为输出层,其中w1-w8、b1-b2是参数,输出结果为f(o1)和f(o2),f(x)为sigmoid激活函数,f(x)=1/(1+e-x)。
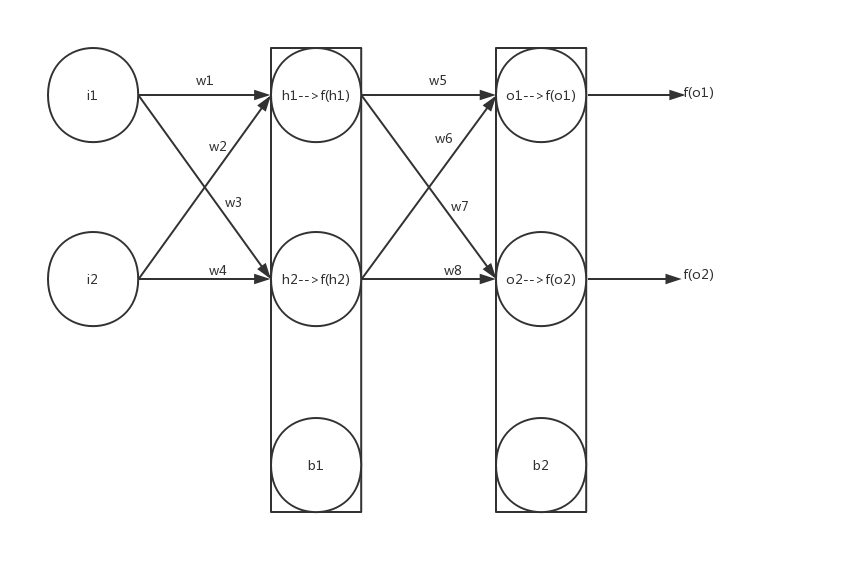
现在我们假设输入了i1和i2,并为所有参数赋予初始值,经过仔细的计算,最终会得到结果f(o1)和f(o2),而我们期望得到t1和t2作为初始结果,那么输出结果与预期值会有一个误差E,我们定义误差(损失)函数为
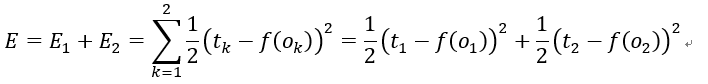
这是最常见的损失函数形式,其中1/2是为了使得之后对E求导的结果更加简洁,不用也是可以的。我们为什么要定义误差(损失)函数?因为定义一个损失函数就把我们的目标“使得预测结果和期望值的误差为0”转化为数学上的最小值问题 ,这种转化思想在研究中是无处不在且十分重要。为什么误差(损失)函数是这种形式?我们当然可以定义tk-f(ok)的绝对值或者是它的n次方作为损失函数,但是绝对值函数不具有求导的很好的性质,而更高(偶数)次方也不会比二次方的效果好很多,而且二次方易于求导,比高次方更利于节省计算,至于奇数次方的损失函数会落入损失抵消的窘境:两个误差为+1和-1,但误差函数为0。实际上还有其他形式的损失函数,但有一点是共同的:误差函数的合适与否往往决定了你的神经网络最终能不能达到你想要的效果。
有了误差函数和网络结构,我们以w1为例,看其对整体误差E产生了多少影响,也就是要看整体误差E对w1求偏导的值有多大。首先E对w1求导,根据链式求导法则,我们可以将其展开为以下形式:
其中![]() 和sigmoid函数及其导数
和sigmoid函数及其导数![]() ,
,
我们可以得到![]() 和
和![]()
,这样后两部分都能被表示出来,然后我们求第一部分,下面我把链式求导的每个分支都用不同颜色标注出来,便于理解:

其中使用到的条件如下,这些条件都可以从神经网络结构中得到,写在这里供大家验证。
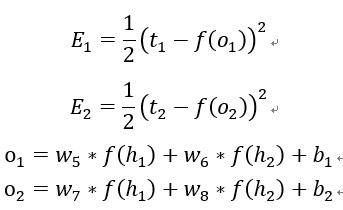
这样就求出∂E/∂w1的表达式,带入初始值就能得到具体的值,更新w1用的是梯度下降法,其中α是学习率,学习率不能设的太大,防止神经网络“过于轻信”,也不能设置的太小,那样神经网络可能会收敛很慢,也就是“过于谨慎”,在一般神经网络中,这个值往往设置的极小,比如0.001或者0.0001。
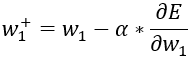
同理,w2-w4的权重也如此更新,但w5-w8的推导步骤要更少,以w5为例:

至此,反向传播的算法原理就讲完了,如果你去知乎上问“如何用最简洁的语言解释反向传播算法?”,答案肯定是四个字:链式求导。它的本质也确实是链式求导,而梯度更新部分是照搬了梯度下降法的公式和方法。从我的认识来看,它最大的贡献是点明了一个问题:神经网络是可以求导的。因为在反向传播算法之前,无数大神纠结于神经网络的复杂,或者是相当程度上被其“非线性”的性质迷惑,非线性性质显示了神经网络处理非线性任务(复杂任务)的潜力,但同时也使得它“似乎”属于非线性系统的范畴,导致很多线性范畴的的数学算法无法使用。直到反向传播算法指出了神经网络的“非线性”之下隐藏的“线性”,并用数学上的链式求导法则漂亮的解决了求导的问题,再用梯度下降法来更新权值,最终为神经网络构建了一条有效的学习路径。可以说,没有反向传播算法,神经网络就无法开始学习的过程。
借鉴另一位博主的代码,我稍微修改了一些地方放到下面供大家分析:


1 import random 2 import math 3 import copy 4 import matplotlib.pyplot as plt 5 # 画图 plt不支持中文,但是可以通过以下方法设置修复 6 plt.rcParams['font.sans-serif']=['SimHei'] 7 plt.rcParams['axes.unicode_minus'] = False 8 9 # 参数解释: 10 # "pd_" :偏导的前缀 11 # "w_ho" :隐含层到输出层的权重系数索引 12 # "w_ih" :输入层到隐含层的权重系数的索引 13 14 # # 神经网络参数 15 # alpha = 0.5 16 # num_inputs=2 17 # num_hidden=2 18 # num_outputs=2 19 # hidden_layer_weights=[0.15, 0.2, 0.25, 0.3] 20 # hidden_layer_bias=0.35 21 # output_layer_weights=[0.4, 0.45, 0.5, 0.55] 22 # output_layer_bias=0.64 23 # inputs=[0.05, 0.1] # 输入值 24 # outputs=[0.01, 0.09] # 真实值 25 26 class NeuralNetwork: 27 alpha = 0.5 28 29 def __init__(self, num_inputs, num_hidden, num_outputs, hidden_layer_weights=None, hidden_layer_bias=None, 30 output_layer_weights=None, output_layer_bias=None): 31 self.num_inputs = num_inputs # 输入层神经元的个数 32 # 生成结构 33 self.hidden_layer = NeuronLayer(num_hidden, hidden_layer_bias) # 生成隐藏层 34 self.output_layer = NeuronLayer(num_outputs, output_layer_bias) # 生成输出层 35 # 生成权重 36 self.init_weights_from_inputs_to_hidden_layer_neurons(hidden_layer_weights) # 输入层到隐藏层 37 self.init_weights_from_hidden_layer_neurons_to_output_layer_neurons(output_layer_weights) # 隐藏层到输出层 38 39 # 初始化输入层到隐藏层的weight 40 def init_weights_from_inputs_to_hidden_layer_neurons(self, hidden_layer_weights): # 输入隐藏层weight 41 weight_num = 0 42 for h in range(len(self.hidden_layer.neurons)): # 遍历隐藏层神经元 43 for i in range(self.num_inputs): # 遍历隐藏层的输入,也就是输入层 44 if not hidden_layer_weights: # 如果隐藏层权重是0,则赋予随机数 45 self.hidden_layer.neurons[h].weights.append(random.random()) 46 else: # 否则设定相应权重。 47 self.hidden_layer.neurons[h].weights.append(hidden_layer_weights[weight_num]) 48 weight_num += 1 49 # 记录初始weight 50 self.hidden_layer.neurons[h].record_parameters() 51 52 # 初始化隐藏层到输出层的weight 53 def init_weights_from_hidden_layer_neurons_to_output_layer_neurons(self, output_layer_weights): 54 weight_num = 0 55 for o in range(len(self.output_layer.neurons)): 56 for h in range(len(self.hidden_layer.neurons)): 57 if not output_layer_weights: 58 self.output_layer.neurons[o].weights.append(random.random()) 59 else: 60 self.output_layer.neurons[o].weights.append(output_layer_weights[weight_num]) 61 weight_num += 1 62 # 记录初始weight 63 self.output_layer.neurons[o].record_parameters() 64 65 # 打印神经结构信息 66 def inspect(self): 67 print('------') 68 print('* Inputs: {}'.format(self.num_inputs)) 69 print('------') 70 print('Hidden Layer') 71 self.hidden_layer.inspect() 72 print('------') 73 print('* Output Layer') 74 self.output_layer.inspect() 75 print('------') 76 # 结果可视化 77 def visualize(self,x): 78 print('------') 79 print('* Inputs: {}'.format(self.num_inputs)) 80 print('------') 81 print('Hidden Layer') 82 Hidden_weights=self.hidden_layer.visualize() 83 84 weights_num=1 85 for i in range(len(Hidden_weights)): 86 for j in range(len(Hidden_weights[i])): 87 # plt.plot(range(x + 1), Hidden_weights[i][j],label='Hidden Layer'+'第'+str(i)+'个神经元'+'第'+str(j)+'个权重') 88 plt.plot(range(x + 1), Hidden_weights[i][j],label='w'+str(weights_num)) 89 weights_num+=1 90 #[m,n]=Hidden_weights 91 print('------') 92 print('* Output Layer') 93 Output_weights = self.output_layer.visualize() 94 for i in range(len(Output_weights)): 95 for j in range(len(Output_weights[i])): 96 # plt.plot(range(x + 1), Output_weights[i][j],label='Output Layer'+'第'+str(i)+'个神经元'+'第'+str(j)+'个权重') 97 plt.plot(range(x + 1), Output_weights[i][j], label='w'+str(weights_num)) 98 weights_num += 1 99 print('------') 100 101 plt.legend(loc='best') # 自动选择图例显示位置 102 plt.show() 103 return 104 105 # 前向计算,调用隐藏层利用输入值计算,调用输出层利用隐藏层输出值计算 106 def feed_forward(self, inputs): 107 hidden_layer_outputs = self.hidden_layer.feed_forward(inputs) 108 return self.output_layer.feed_forward(hidden_layer_outputs) 109 110 # 训练 111 def train(self, i, t): 112 self.feed_forward(i) # 先前向运算一次 113 114 # 1. 计算输出层神经元的偏导数∂E/∂o1、∂E/∂o2 115 pd_E_pd_input_OutputLayer = [0] * len(self.output_layer.neurons) # 准备输出值的格式[0,0] 116 for o in range(len(self.output_layer.neurons)): # 遍历输出层神经元 117 # ∂E/∂o1=∂E/∂f(o1)*∂f(o1)/∂o1=-(t-o1) * f(o1)*(1-f(o1)) 118 # ∂E/∂o2=∂E/∂f(o2)*∂f(o2)/∂o1=-(t-o2) * f(o2)*(1-f(o2)) 119 pd_E_pd_input_OutputLayer[o] = self.output_layer.neurons[o].calculate_pd_E_pd_input(t[o]) 120 121 122 # 2. 计算隐含层神经元的偏导数∂E/∂h1、∂E/∂h2 123 pd_E_pd_input_HiddenLayer = [0] * len(self.hidden_layer.neurons) # 准备隐含层的格式[0,0] 124 for h in range(len(self.hidden_layer.neurons)): # 遍历隐含层神经元 125 # ∂E/∂f(h1) = ∂E1/∂f(h1)+∂E2/∂f(h1) 126 pd_E_pd_output_HiddenLayer = 0 127 for o in range(len(self.output_layer.neurons)): 128 # ∂E/∂f(h1)=∂E/∂o1 * ∂o1/∂f(h1) ∂E/∂o1对应公式中红、黄乘积, ∂o1/∂f(h1)对应蓝色偏导乘积 129 pd_E_pd_output_HiddenLayer += pd_E_pd_input_OutputLayer[o] * self.output_layer.neurons[o].weights[h] 130 131 # ∂E/∂h1=∂E/∂f(h1) * ∂f(h1)/∂h1 在上面的结果上乘以∂f(h1)/∂h1,此时距离计算出偏导只差∂h1/∂w1=i1 132 pd_E_pd_input_HiddenLayer[h] = pd_E_pd_output_HiddenLayer * self.hidden_layer.neurons[h].calculate_pd_output_pd_input() 133 134 # 3. 更新输出层权重系数 更新w5-w8 135 for o in range(len(self.output_layer.neurons)): # 遍历输出层神经元 136 for w_ho in range(len(self.output_layer.neurons[o].weights)): # 遍历输出层每个神经元的权重 137 # 例如 ∂E/∂w5=∂E/∂o1*∂o1/∂w5 138 pd_E_pd_w = pd_E_pd_input_OutputLayer[o] * self.output_layer.neurons[o].calculate_pd_input_pd_w(w_ho) 139 # w^+ =w - α * ∂E/∂w 梯度以α的学习率更新 140 self.output_layer.neurons[o].weights[w_ho] -= self.alpha * pd_E_pd_w 141 # 记录参数变化 142 self.output_layer.neurons[o].record_parameters() 143 # 4. 更新隐含层的权重系数 更新w1-w4 144 for h in range(len(self.hidden_layer.neurons)): 145 for w_ih in range(len(self.hidden_layer.neurons[h].weights)): 146 # 例如 ∂E/∂w1=∂E/∂o1*∂o1/∂w1 147 pd_E_pd_w = pd_E_pd_input_HiddenLayer[h] * self.hidden_layer.neurons[h].calculate_pd_input_pd_w(w_ih) 148 # w^+ =w - α * ∂E/∂w 149 self.hidden_layer.neurons[h].weights[w_ih] -= self.alpha * pd_E_pd_w 150 151 # 记录参数变化 152 self.hidden_layer.neurons[h].record_parameters() 153 154 # 计算总的误差 155 def calculate_E(self, training_sets): 156 E = 0 157 for t in range(len(training_sets)): 158 training_inputs, training_outputs = training_sets[t] 159 self.feed_forward(training_inputs) 160 for o in range(len(training_outputs)): 161 E += self.output_layer.neurons[o].calculate_E(training_outputs[o]) 162 return E 163 164 165 # 生成神经层的类 166 class NeuronLayer: 167 def __init__(self, num_neurons, bias): 168 169 # 同一层的神经元共享一个截距项b 170 self.bias = bias if bias else random.random() # 如果截距为0则设为随机数 171 172 self.neurons = [] 173 for i in range(num_neurons): # 生成num_neurons个神经元 174 self.neurons.append(Neuron(self.bias)) # 赋予该层神经元同一个权重 175 176 # 打印该层神经元详细信息 177 def inspect(self): 178 print('Neurons:', len(self.neurons)) 179 for n in range(len(self.neurons)): 180 print(' Neuron', n) 181 for w in range(len(self.neurons[n].weights)): 182 print(' Weight:', self.neurons[n].weights[w]) 183 print(' Weight_change:') 184 for i in range(len(self.neurons[n].weights_change)): 185 print(' ',self.neurons[n].weights_change[i][w]) 186 print(' Bias:', self.bias) 187 188 def visualize(self): 189 output=[] 190 for n in range(len(self.neurons)): # 本层第几个神经元 191 print(' Neuron', n) 192 for w in range(len(self.neurons[n].weights)): # 本神经元第几个权重 193 print(' Weight:', self.neurons[n].weights[w]) 194 print(' Bias:', self.bias) 195 output.append(list(zip(*self.neurons[n].weights_change))) 196 return output 197 # 前向计算,让每个神经元计算并返回输出结果 198 def feed_forward(self, inputs): 199 outputs = [] 200 for neuron in self.neurons: 201 outputs.append(neuron.calculate_output(inputs)) 202 return outputs 203 204 # 获得神经元输出 205 def get_outputs(self): 206 outputs = [] 207 for neuron in self.neurons: 208 outputs.append(neuron.output) 209 return outputs 210 211 # 生成神经元的类 212 class Neuron: 213 def __init__(self, bias): # 两个成员 偏置(传入)和权重设定为空 214 self.bias = bias 215 self.weights = [] 216 self.bias_change = [] 217 self.weights_change = [] 218 219 def record_parameters(self): 220 self.weights_change.append(copy.copy(self.weights)) 221 # 由于append存的指针,所以必须拷贝一下再append,避免数据自动变动 222 return True 223 224 def calculate_output(self, inputs): # 计算输出 使用sigmoid激活函数 225 self.inputs = inputs 226 self.output = self.squash(self.calculate_input()) 227 return self.output 228 229 def calculate_input(self): # 计算输入 使用循环计算若干个输入的加权和 230 total = 0 231 for i in range(len(self.inputs)): 232 total += self.inputs[i] * self.weights[i] 233 return total + self.bias 234 235 # 激活函数sigmoid 236 def squash(self, total_net_input): 237 return 1 / (1 + math.exp(-total_net_input)) 238 239 # 计算偏导数结果 240 def calculate_pd_E_pd_input(self, t): 241 return self.calculate_pd_E_pd_output(t) * self.calculate_pd_output_pd_input() 242 243 # 每一个神经元的误差是由平方差公式计算的 244 def calculate_E(self, t): 245 return 0.5 * (t - self.output) ** 2 # python乘方写法 246 247 # 返回-(t1-o1) 第一部分 248 def calculate_pd_E_pd_output(self, t): 249 return -(t - self.output) 250 251 # 返回f(x)(1-f(x)) 第二部分 252 def calculate_pd_output_pd_input(self): 253 return self.output * (1 - self.output) 254 255 # 返回w 第三部分 256 def calculate_pd_input_pd_w(self, index): 257 return self.inputs[index] 258 259 # 例子: 260 261 nn = NeuralNetwork(2, 2, 2, hidden_layer_weights=[0.15, 0.2, 0.25, 0.3], hidden_layer_bias=0.35, 262 output_layer_weights=[0.4, 0.45, 0.5, 0.55], output_layer_bias=0.6) 263 T=1000 # 迭代次数 264 for i in range(T): 265 nn.train([0.05, 0.1], [0.01, 0.99]) 266 print(i, round(nn.calculate_E([[[0.05, 0.1], [0.01, 0.99]]]), 9)) 267 nn.visualize(T)
训练迭代了1000次并显示w1-w8的参数变化图,可见,一开始参数变化很快,之后就变化的很缓慢,表示参数训练开始收敛了,1000次迭代可以把误差减小到0.001114349,检查参数的变动情况是判断模型是否能收敛的方法之一。代码的解释基本都写在注释了,有需要的可以跑起来看看。

一、总结
这篇博客也花了很长的时间,主要是在改代码的时候遇到了几个不熟悉的python语法点导致坑了很久,比如list的append()实际上只存储了数据的引用,zip的用法,迭代器的用法,参考博客的代码结构整洁精致让我学到了很多,若有什么疏忽的地方,欢迎大家指正!
参考文献
http://www.cnblogs.com/charlotte77/p/5629865.html
http://galaxy.agh.edu.pl/~vlsi/AI/backp_t_en/backprop.html
https://www.cnblogs.com/wlzy/p/7751297.html


