《FPGA数字信号处理》基于FPGA的32点并行FFT/IFFT设计_并行fft设计

本人FPGA小白，只关注FPGA具体功能实现。如以下描述有误，望评论区指正！以下内容，纯手打，严禁未经过同意擅自转载，谢谢！

1、基2按时间抽取的FFT流程

相比于基2算法，基4算法对本设计（32点FFT）运算的复杂度并没有显著的降低。
基2按时间抽取的FFT蝶形运算如下图所示：

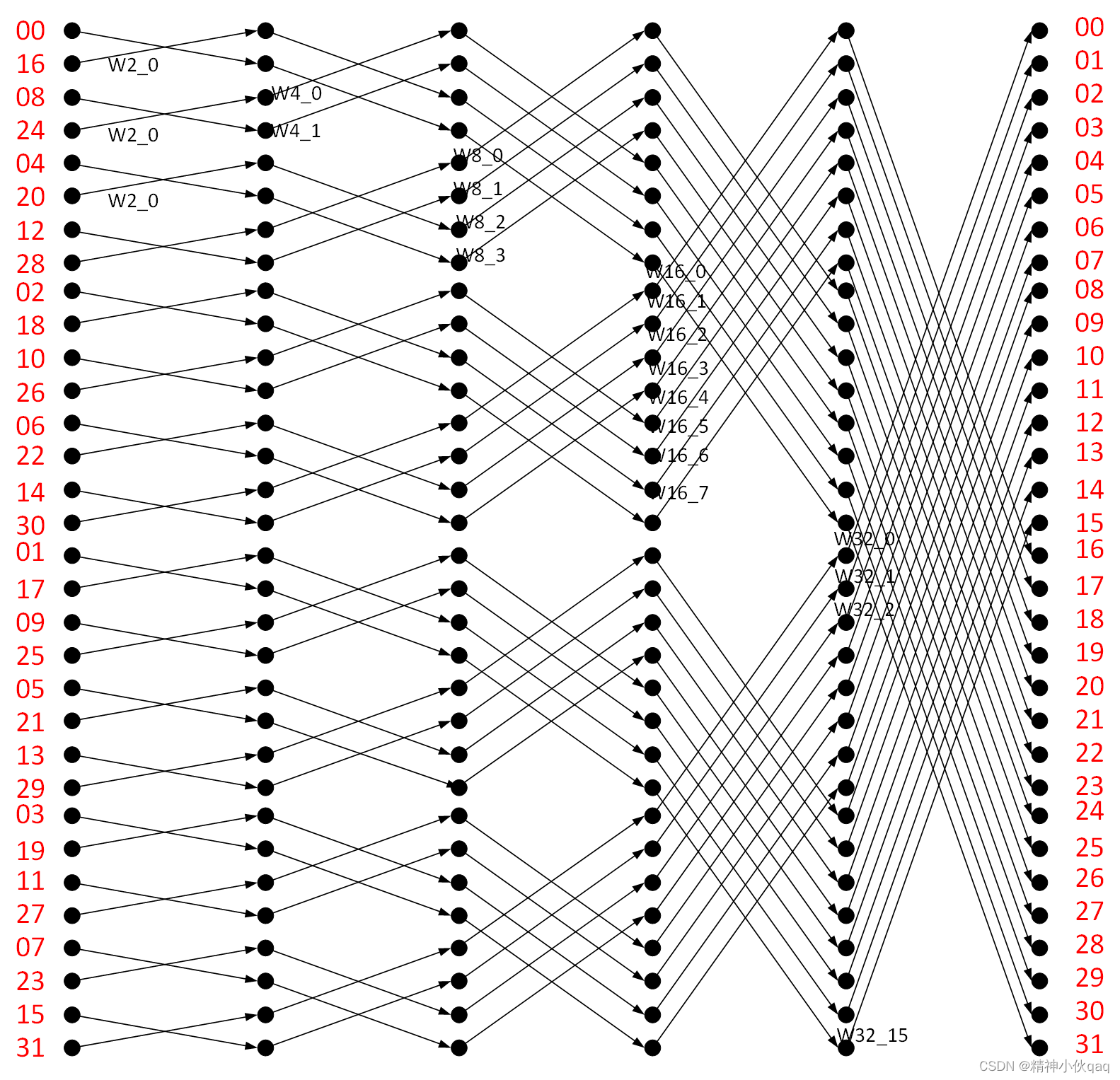
可以发现输入端与输出端的序列顺序是不一样的，若想得到输出端为自然顺序（0-31）的序列，则需要将输入端的序列按一定的规则重新排列。
复杂的公式推导这里就不列了，需要的可以随便在一本数字信号处理的书中找到，这里只说明怎么重新排列输入端的序列顺序。
这里的关键字是“基2”和“按时间抽取”。

按时间抽取的大流程是：将序列按时间顺序抽取成奇偶项，并对得到的序列继续抽取，直到抽取后得到的序列长度为2（基2）。此时重新排列即为FFT蝶形运算的输入端序列顺序。

2、matlab FFT算法实现

算法比较简单，只有一个核心运算：蝶形运算。

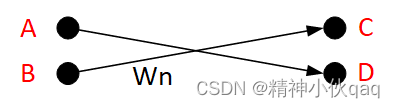
如上图所示：C = A + B * Wn D = A - B * Wn，其中Wn为蝶形因子

matlab 蝶形运算

function [outputArg0,outputArg1] = butterfly(arg0,arg1,butterfly_factor)
%BUTTERFLY 蝶形运算
%   此处显示详细说明
    outputArg0 = arg0 + arg1 * butterfly_factor;
    outputArg1 = arg0 - arg1 * butterfly_factor;

end
1
2
3
4
5
6
7

matlab 蝶形因子计算

N = 32;

BF_factor_L0 = linspace(0,N/32-1,N/32);
BF_factor_L0 = exp(-1j*2*pi/2.*BF_factor_L0) ; % 蝶形因子 * 32767 

BF_factor_L1 = linspace(0,N/16-1,N/16);
BF_factor_L1 = exp(-1j*2*pi/4.*BF_factor_L1); % 蝶形因子 * 32767

BF_factor_L2 = linspace(0,N/8-1,N/8);
BF_factor_L2 = exp(-1j*2*pi/8.*BF_factor_L2); % 蝶形因子 * 32767

BF_factor_L3 = linspace(0,N/4-1,N/4);
BF_factor_L3 = exp(-1j*2*pi/16.*BF_factor_L3); % 蝶形因子 * 32767

BF_factor_L4 = linspace(0,N/2-1,N/2);
BF_factor_L4 = exp(-1j*2*pi/32.*BF_factor_L4); % 蝶形因子 * 32767

end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

matlab 第0级蝶形运算

% Level_0
[result_L0(1) ,result_L0(2)] = butterfly(data(1) ,data(17),BF_factor_L0(1));
[result_L0(3) ,result_L0(4)] = butterfly(data(9) ,data(25),BF_factor_L0(1));
[result_L0(5) ,result_L0(6)] = butterfly(data(5) ,data(21),BF_factor_L0(1));
[result_L0(7) ,result_L0(8)] = butterfly(data(13),data(29),BF_factor_L0(1));
[result_L0(9) ,result_L0(10)]= butterfly(data(3) ,data(19),BF_factor_L0(1));
[result_L0(11),result_L0(12)]= butterfly(data(11),data(27),BF_factor_L0(1));
[result_L0(13),result_L0(14)]= butterfly(data(7) ,data(23),BF_factor_L0(1));
[result_L0(15),result_L0(16)]= butterfly(data(15),data(31),BF_factor_L0(1));
[result_L0(17),result_L0(18)]= butterfly(data(2) ,data(18),BF_factor_L0(1));
[result_L0(19),result_L0(20)]= butterfly(data(10),data(26),BF_factor_L0(1));
[result_L0(21),result_L0(22)]= butterfly(data(6) ,data(22),BF_factor_L0(1));
[result_L0(23),result_L0(24)]= butterfly(data(14),data(30),BF_factor_L0(1));
[result_L0(25),result_L0(26)]= butterfly(data(4) ,data(20),BF_factor_L0(1));
[result_L0(27),result_L0(28)]= butterfly(data(12),data(28),BF_factor_L0(1));
[result_L0(29),result_L0(30)]= butterfly(data(8) ,data(24),BF_factor_L0(1));
[result_L0(31),result_L0(32)]= butterfly(data(16),data(32),BF_factor_L0(1));
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

matlab 第1级蝶形运算

% Level_1
[result_L1(1) ,result_L1(3)] = butterfly(result_L0(1) ,result_L0(3) ,BF_factor_L1(1));
[result_L1(2) ,result_L1(4)] = butterfly(result_L0(2) ,result_L0(4) ,BF_factor_L1(2));
[result_L1(5) ,result_L1(7)] = butterfly(result_L0(5) ,result_L0(7) ,BF_factor_L1(1));
[result_L1(6) ,result_L1(8)] = butterfly(result_L0(6) ,result_L0(8) ,BF_factor_L1(2));
[result_L1(9) ,result_L1(11)]= butterfly(result_L0(9) ,result_L0(11),BF_factor_L1(1));
[result_L1(10),result_L1(12)]= butterfly(result_L0(10),result_L0(12),BF_factor_L1(2));
[result_L1(13),result_L1(15)]= butterfly(result_L0(13),result_L0(15),BF_factor_L1(1));
[result_L1(14),result_L1(16)]= butterfly(result_L0(14),result_L0(16),BF_factor_L1(2));
[result_L1(17),result_L1(19)]= butterfly(result_L0(17),result_L0(19),BF_factor_L1(1));
[result_L1(18),result_L1(20)]= butterfly(result_L0(18),result_L0(20),BF_factor_L1(2));
[result_L1(21),result_L1(23)]= butterfly(result_L0(21),result_L0(23),BF_factor_L1(1));
[result_L1(22),result_L1(24)]= butterfly(result_L0(22),result_L0(24),BF_factor_L1(2));
[result_L1(25),result_L1(27)]= butterfly(result_L0(25),result_L0(27),BF_factor_L1(1));
[result_L1(26),result_L1(28)]= butterfly(result_L0(26),result_L0(28),BF_factor_L1(2));
[result_L1(29),result_L1(31)]= butterfly(result_L0(29),result_L0(31),BF_factor_L1(1));
[result_L1(30),result_L1(32)]= butterfly(result_L0(30),result_L0(32),BF_factor_L1(2));
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

matlab 第2级蝶形运算

% Level_2
[result_L2(1) ,result_L2(5)] = butterfly(result_L1(1) ,result_L1(5) ,BF_factor_L2(1));
[result_L2(2) ,result_L2(6)] = butterfly(result_L1(2) ,result_L1(6) ,BF_factor_L2(2));
[result_L2(3) ,result_L2(7)] = butterfly(result_L1(3) ,result_L1(7) ,BF_factor_L2(3));
[result_L2(4) ,result_L2(8)] = butterfly(result_L1(4) ,result_L1(8) ,BF_factor_L2(4));
[result_L2(9) ,result_L2(13)]= butterfly(result_L1(9) ,result_L1(13),BF_factor_L2(1));
[result_L2(10),result_L2(14)]= butterfly(result_L1(10),result_L1(14),BF_factor_L2(2));
[result_L2(11),result_L2(15)]= butterfly(result_L1(11),result_L1(15),BF_factor_L2(3));
[result_L2(12),result_L2(16)]= butterfly(result_L1(12),result_L1(16),BF_factor_L2(4));
[result_L2(17),result_L2(21)]= butterfly(result_L1(17),result_L1(21),BF_factor_L2(1));
[result_L2(18),result_L2(22)]= butterfly(result_L1(18),result_L1(22),BF_factor_L2(2));
[result_L2(19),result_L2(23)]= butterfly(result_L1(19),result_L1(23),BF_factor_L2(3));
[result_L2(20),result_L2(24)]= butterfly(result_L1(20),result_L1(24),BF_factor_L2(4));
[result_L2(25),result_L2(29)]= butterfly(result_L1(25),result_L1(29),BF_factor_L2(1));
[result_L2(26),result_L2(30)]= butterfly(result_L1(26),result_L1(30),BF_factor_L2(2));
[result_L2(27),result_L2(31)]= butterfly(result_L1(27),result_L1(31),BF_factor_L2(3));
[result_L2(28),result_L2(32)]= butterfly(result_L1(28),result_L1(32),BF_factor_L2(4));
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

matlab 第3级蝶形运算

% Level_3
[result_L3(1) ,result_L3(9)] = butterfly(result_L2(1) ,result_L2(9) ,BF_factor_L3(1));
[result_L3(2) ,result_L3(10)]= butterfly(result_L2(2) ,result_L2(10),BF_factor_L3(2));
[result_L3(3) ,result_L3(11)]= butterfly(result_L2(3) ,result_L2(11),BF_factor_L3(3));
[result_L3(4) ,result_L3(12)]= butterfly(result_L2(4) ,result_L2(12),BF_factor_L3(4));
[result_L3(5) ,result_L3(13)]= butterfly(result_L2(5) ,result_L2(13),BF_factor_L3(5));
[result_L3(6) ,result_L3(14)]= butterfly(result_L2(6) ,result_L2(14),BF_factor_L3(6));
[result_L3(7) ,result_L3(15)]= butterfly(result_L2(7) ,result_L2(15),BF_factor_L3(7));
[result_L3(8) ,result_L3(16)]= butterfly(result_L2(8) ,result_L2(16),BF_factor_L3(8));
[result_L3(17),result_L3(25)]= butterfly(result_L2(17),result_L2(25),BF_factor_L3(1));
[result_L3(18),result_L3(26)]= butterfly(result_L2(18),result_L2(26),BF_factor_L3(2));
[result_L3(19),result_L3(27)]= butterfly(result_L2(19),result_L2(27),BF_factor_L3(3));
[result_L3(20),result_L3(28)]= butterfly(result_L2(20),result_L2(28),BF_factor_L3(4));
[result_L3(21),result_L3(29)]= butterfly(result_L2(21),result_L2(29),BF_factor_L3(5));
[result_L3(22),result_L3(30)]= butterfly(result_L2(22),result_L2(30),BF_factor_L3(6));
[result_L3(23),result_L3(31)]= butterfly(result_L2(23),result_L2(31),BF_factor_L3(7));
[result_L3(24),result_L3(32)]= butterfly(result_L2(24),result_L2(32),BF_factor_L3(8));
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

matlab 第4级蝶形运算

% Level_4

[result_L4(1) ,result_L4(17)]= butterfly(result_L3(1) ,result_L3(17),BF_factor_L4(1));
[result_L4(2) ,result_L4(18)]= butterfly(result_L3(2) ,result_L3(18),BF_factor_L4(2));
[result_L4(3) ,result_L4(19)]= butterfly(result_L3(3) ,result_L3(19),BF_factor_L4(3));
[result_L4(4) ,result_L4(20)]= butterfly(result_L3(4) ,result_L3(20),BF_factor_L4(4));
[result_L4(5) ,result_L4(21)]= butterfly(result_L3(5) ,result_L3(21),BF_factor_L4(5));
[result_L4(6) ,result_L4(22)]= butterfly(result_L3(6) ,result_L3(22),BF_factor_L4(6));
[result_L4(7) ,result_L4(23)]= butterfly(result_L3(7) ,result_L3(23),BF_factor_L4(7));
[result_L4(8) ,result_L4(24)]= butterfly(result_L3(8) ,result_L3(24),BF_factor_L4(8));
[result_L4(9) ,result_L4(25)]= butterfly(result_L3(9) ,result_L3(25),BF_factor_L4(9));
[result_L4(10),result_L4(26)]= butterfly(result_L3(10),result_L3(26),BF_factor_L4(10));
[result_L4(11),result_L4(27)]= butterfly(result_L3(11),result_L3(27),BF_factor_L4(11));
[result_L4(12),result_L4(28)]= butterfly(result_L3(12),result_L3(28),BF_factor_L4(12));
[result_L4(13),result_L4(29)]= butterfly(result_L3(13),result_L3(29),BF_factor_L4(13));
[result_L4(14),result_L4(30)]= butterfly(result_L3(14),result_L3(30),BF_factor_L4(14));
[result_L4(15),result_L4(31)]= butterfly(result_L3(15),result_L3(31),BF_factor_L4(15));
[result_L4(16),result_L4(32)]= butterfly(result_L3(16),result_L3(32),BF_factor_L4(16));
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

与matlab 库函数FFT运算比较

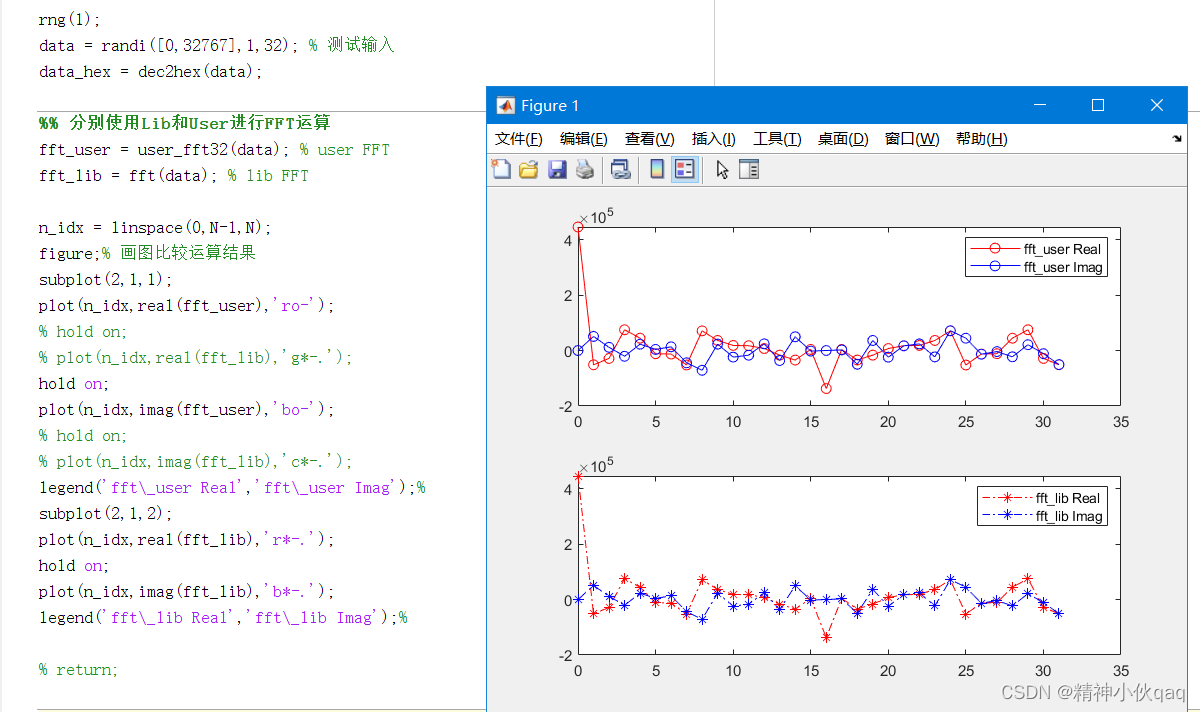
通过对比可知，编写的FFT输出结果与调用库函数FFT结果基本一致。

FPGA FFT算法实现

FPGA中32点并行FFT算法的实现流程与matlab中是完全一致的。工程结构如下：

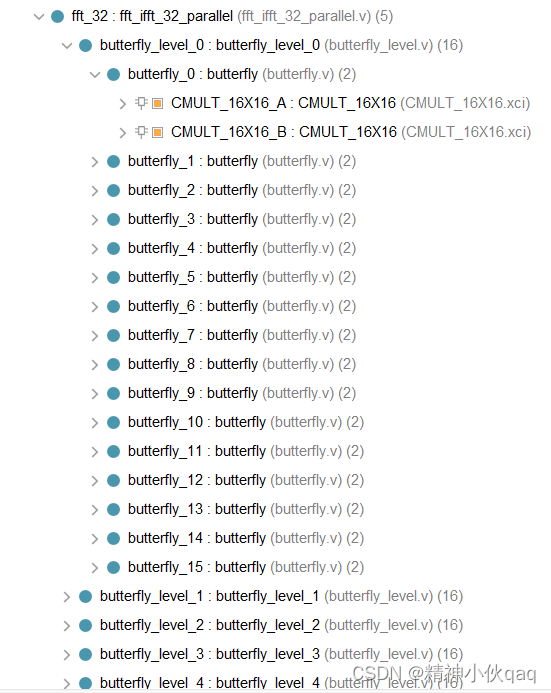
3、matlab与FPGA实现的结果对比

matlab输出结果

FPGA输出结果

FPGA输出结果实部

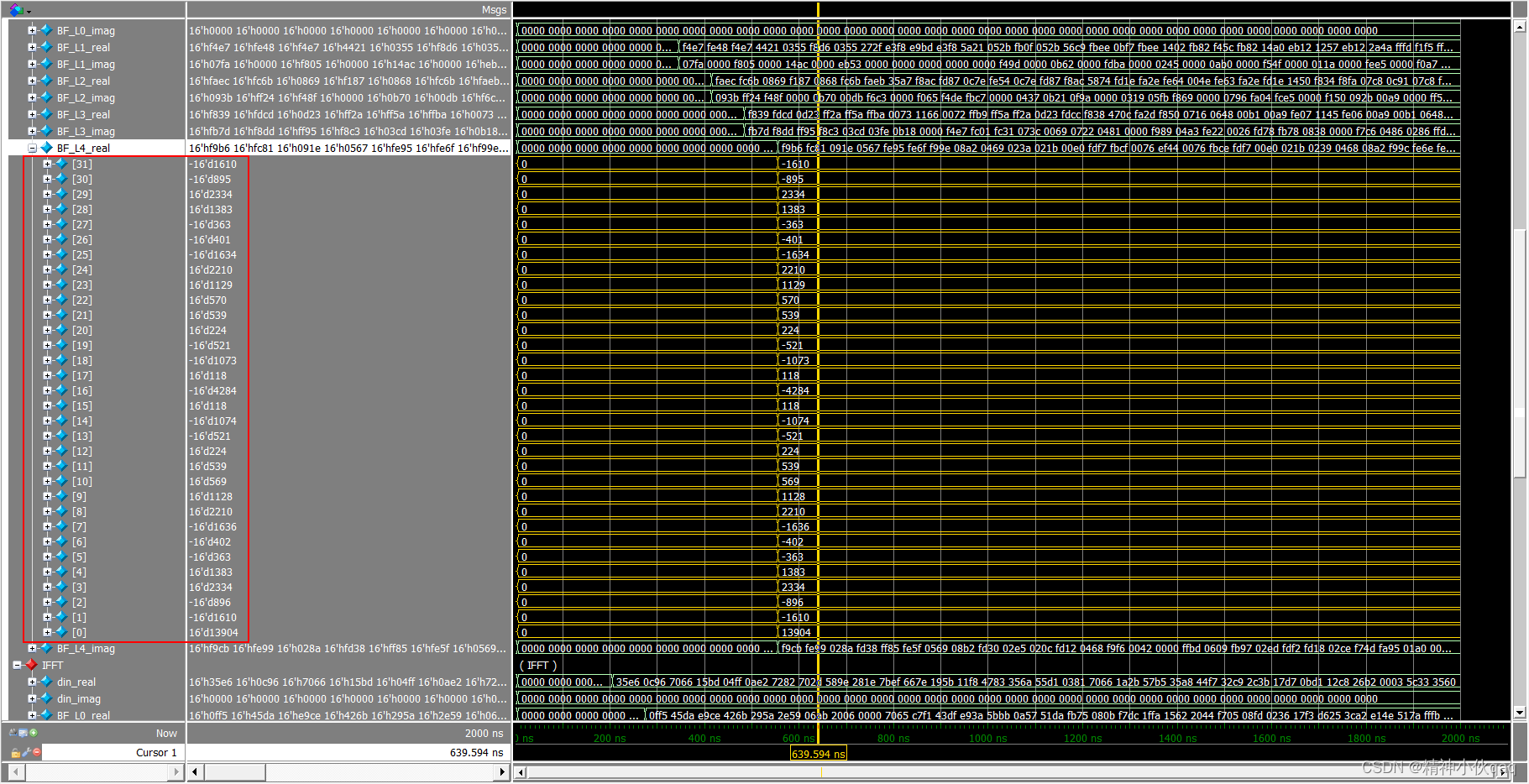
FPGA输出结果虚部

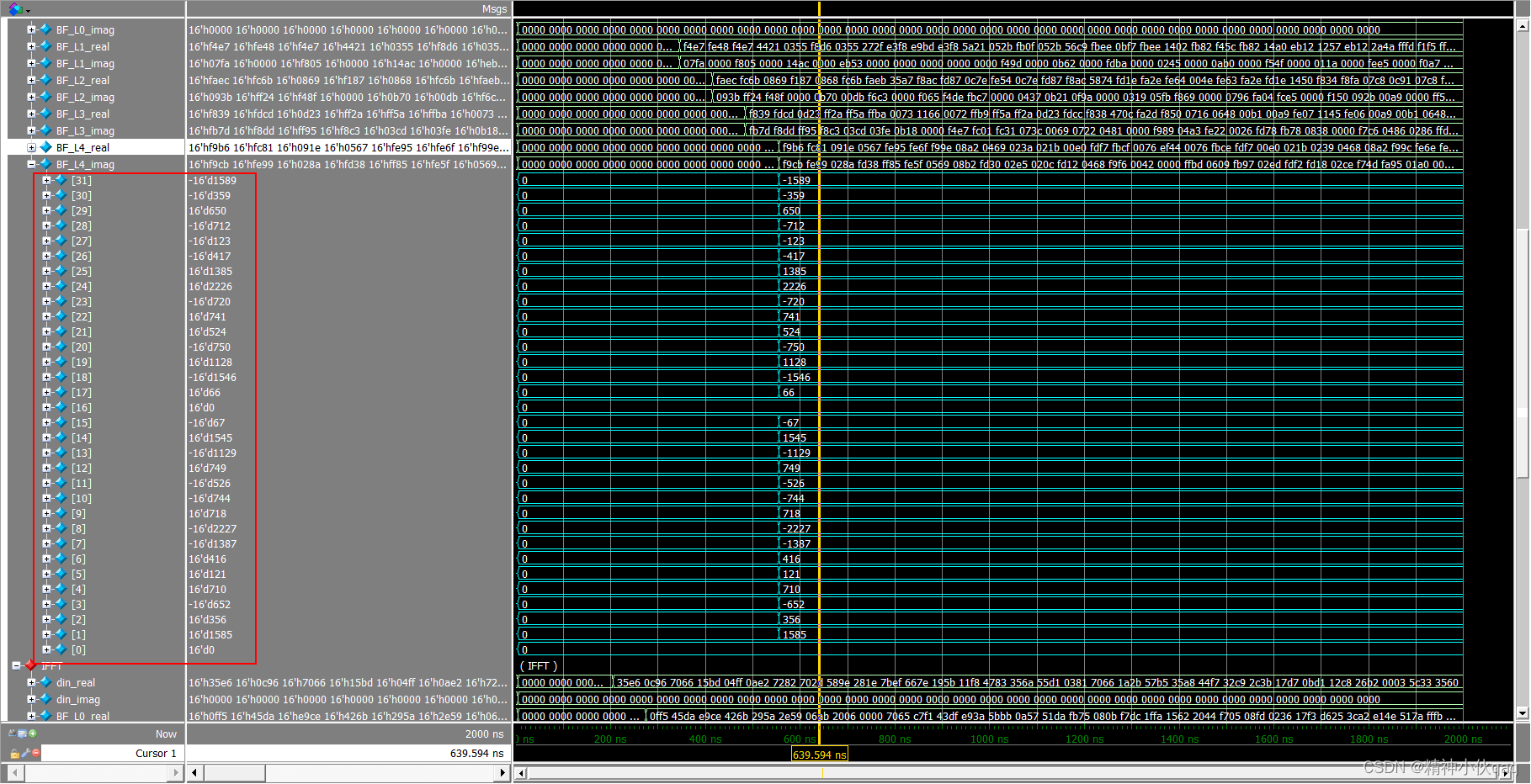
4、IFFT实现

IFFT实现与FFT实现基本一致，可以通过FFT算法得到IFFT的结果。
1、将IFFT的输入序列取共轭；
2、进行FFT运算；
3、将FFT运算结果取共轭，得到的结果就是原序列IFFT的结果。