【MATLAB】PRM+A star（A*）寻路算法改进_a星算法改进matlab代码

目录

1 原算法链接

2 改进部分

3 改进代码运行效果

1 原算法链接

【MATLAB】PRM+A star（A*）寻路算法实现_一只小白白的博客-CSDN博客

2 改进部分

原算法是在PRM建立好图G后再确定起始点和终止点，这样就存在一个问题，就是原算法没有将设定的起始点和终止点信息纳入图G中，导致A*搜索出来的路径虽然是最优的，但其实那段起始路径（连接起始点和G中起始点的路径）和终止的路径（连接终止点和G中终止点的路径）不是全局最优的，原算法寻路效果如下：

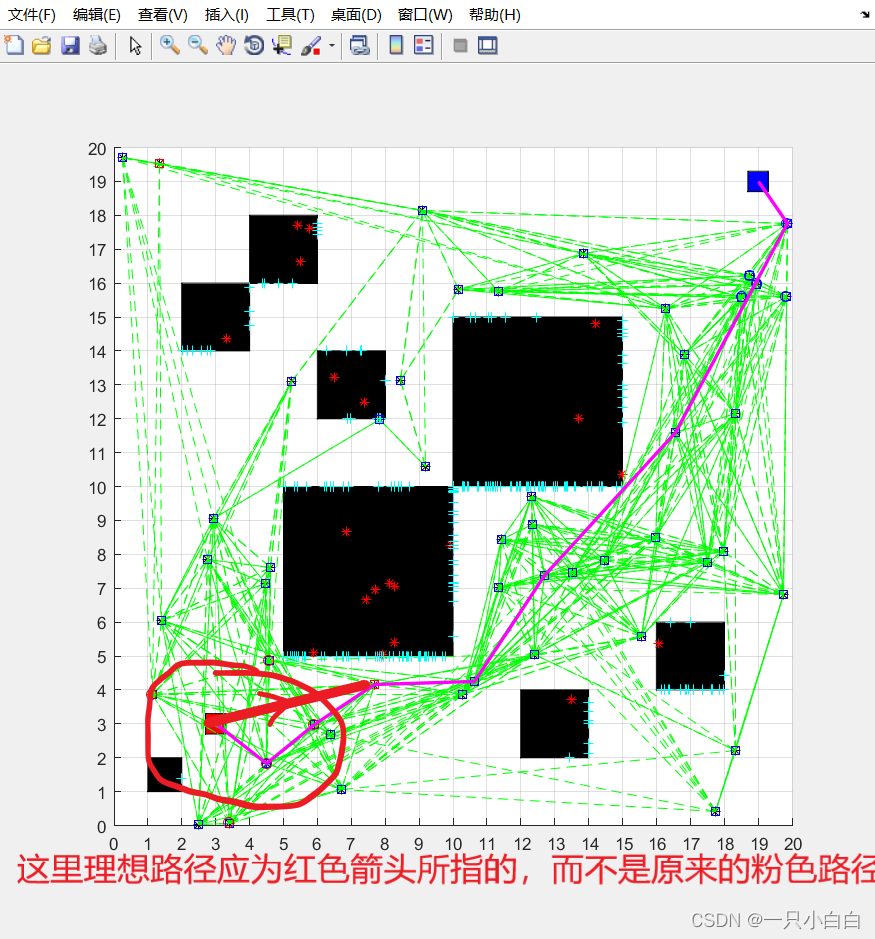
 改进方法也很简单，将设定的起始点和终止点纳入图G中，原本nxn的图变为了（n+2）x（n+2）的图，改进后的PRM算法代码如下：

function [allV,graph,Index_startInPRM,Index_endInPRM]= build_PRM(n,k,QLIST,MAX_X,MAX_Y,qset)
% 随机生成节点数组
V=[]; 
% 初始化图的二维数组（n+2 * n+2）----包含起始点和终止点qset
G=zeros(n+2); 
% 障碍物个数
Obstacle_Num = size(QLIST,1);
%% 绘制障碍物模型
for i=1:Obstacle_Num
    Q = [QLIST(i,1:4);QLIST(i,5:8)];
    fill(Q(1,:),Q(2,:),'k');
    hold on
end
%% 初始化图G的相邻节点间边的权值
for i=1:n+2
    for j=1:n+2
        if ~isequal(i,j)
         G(i,j)=inf;
        end
    end
end
%% 随机生成n个节点，判断是否落在障碍物上，如果不在障碍物中，将其加入节点数组V中
% 将初始点和终止点先加入V中
V = [V,qset(:,1)];
V = [V,qset(:,2)];
% 返回搜索初始点和终止点的索引
Index_startInPRM = 1;
Index_endInPRM = 2;
% 随机生成节点加入V中
if Obstacle_Num==0
    while size(V,2)<n+2
        qrand=[MAX_X*rand;MAX_Y*rand];
        V=[V,qrand]; % 由于没有障碍物，直接填充即可
    end
else
    while size(V,2)<n+2
        qrand=[MAX_X*rand;MAX_Y*rand];
        % 存在障碍物时，需要剔除随机生成在障碍物上的点，保留符合条件的点
        for m=1:Obstacle_Num
            Q = [QLIST(m,1:4);QLIST(m,5:8)];
            Q = [Q,Q(:,1)];
            [in,on] = inpolygon(qrand(1),qrand(2),Q(1,:),Q(2,:));
            if (in==1 || on==1)
                plot(qrand(1),qrand(2),'r*'); hold on;
                break;
            elseif m==Obstacle_Num
                V=[V,qrand];
                plot(qrand(1),qrand(2),'k*'); hold on;
            end
        end
    end
end
%% 根据上面生成的n个节点，填充图G的数据
if Obstacle_Num==0
    for j=1:size(V,2)
        % 找出当前节点j邻近的k个节点，找出的邻近点包括自己，且为第一个索引值，即ind(1)
        ind= knnsearch( V', V(:,j)', 'k',k+1);
        ind_temp = [];
        for i=2:size(ind,2)
            % 保证邻近节点Nq不包括自己
            ind_temp = [ind_temp,ind(i)];
            Nq(:,i-1)= V(:,ind(i));
        end
        ind = ind_temp;
        % 遍历这k个节点，因为没有障碍物，所以直接把当前节点与其邻近节点相连即可
        for i=1:size(Nq,2)
            G(j,ind(i))=1; % 如果一直到最后一个障碍物都没有交叉，则此邻近节点与j节点可通行，权值设为1
            G(ind(i),j)=1;
            plot([V(1,j),Nq(1,i)],[V(2,j),Nq(2,i)],'g--');
            pause(0.01);
            hold on
        end        
    end % 结束 for 循环
else
    for j=1:size(V,2)
        plot(V(1,j),V(2,j),'rs'); hold on;
        % 找出当前节点j邻近的k个节点，找出的邻近点包括自己，且为第一个索引值，即ind(1)
        ind= knnsearch( V', V(:,j)', 'k',k+1);
        ind_temp = [];
        % 保证邻近节点Nq不包括自己
        for i=2:size(ind,2)
            ind_temp = [ind_temp,ind(i)];
            Nq(:,i-1)= V(:,ind(i));
            plot(Nq(1,i-1),Nq(2,i-1),'bs'); hold on;
        end
        ind = ind_temp;
        % 遍历这k个节点，如果与父节点连线不与障碍物碰撞，则G中相应权值为1，代表两节点之间可通行
        for i=1:size(Nq,2)
            % 遍历所有障碍物，判断第i个邻近节点与j节点的连线与障碍物是否有交叉
            for m=1:Obstacle_Num
                Q = [QLIST(m,1:4);QLIST(m,5:8)];
                if  isIntersection( V(:,j),Nq(:,i),Q )==1
%                     plot([V(1,j),Nq(1,i)],[V(2,j),Nq(2,i)],'r--');
                    break; % 如果有交叉，直接break，进入下一个邻近节点的判断
                elseif m==Obstacle_Num
                    G(j,ind(i))=1; % 如果一直到最后一个障碍物都没有交叉，则此邻近节点与j节点可通行，权值设为1
                    G(ind(i),j)=1;
                    plot([V(1,j),Nq(1,i)],[V(2,j),Nq(2,i)],'g--');
%                     pause(0.01);
                    hold on
                end
            end
        end            
    end % 结束 for 循环
end % 结束 if和else 判断
 
% 输出图G和节点信息V
allV=V;
graph=G;
 
end

A*算法部分代码不用改动，主函数改动如下：

%%----------------------------------------------
% Author: Yinsong Qu
% Date:   8,14,2023
% Email: quyinsong@hrbeu.edu.cn
%%----------------------------------------------
clc
clear all
close all
%% 1. Run PRM
%get the graph by running PRM and map lot
%V is all the qs'
qset=[3 19;3 19];  % 1st column: q_initial, 2nd: q_goal
n=50; % 随机生成的节点数
k=20; % 每个节点最大允许的邻近子节点数量
% 多边形表示的障碍物
Q1=[1 2 2 1;1 1 2 2];   % 障碍物
Q2=[10 15 15 10;
    10 10 15 15];   % 障碍物
Q3=[5 10 10 5;
    5 5 10 10];   % 障碍物
Q4=[2 4 4 2;14 14 16 16];   % 障碍物
Q5=[4 6 6 4;16 16 18 18];   % 障碍物
Q6=[16 18 18 16;4 4 6 6];   % 障碍物
Q7=[12 14 14 12;2 2 4 4];   % 障碍物
Q8=[6 8 8 6;12 12 14 14];   % 障碍物
% 障碍物列表
QLIST = [Q1(1,1:4),Q1(2,1:4);
         Q2(1,1:4),Q2(2,1:4);
         Q3(1,1:4),Q3(2,1:4);
         Q4(1,1:4),Q4(2,1:4);
         Q5(1,1:4),Q5(2,1:4);
         Q6(1,1:4),Q6(2,1:4);
         Q7(1,1:4),Q7(2,1:4);
         Q8(1,1:4),Q8(2,1:4);];
% QLIST = [];
% QLIST = [Q2(1,1:4),Q2(2,1:4);Q3(1,1:4),Q3(2,1:4)];
% 设置地图范围
MAX_X = 20;
MAX_Y = 20;
% 绘制地图，起始点和终止点
figure(1)
set(gcf, 'Renderer', 'painters');
set(gcf, 'Position', [500, 50, 700, 700]);
set(gca, 'XTick', 0:1:MAX_X);
set(gca, 'YTick', 0:1:MAX_Y);
grid on;
axis equal;        
axis ([0 MAX_X 0 MAX_Y ]);
hold on;
LL = 0.3;
fill([qset(1,1)-LL,qset(1,1)+LL,qset(1,1)+LL,qset(1,1)-LL],[qset(2,1)-LL,qset(2,1)-LL,qset(2,1)+LL,qset(2,1)+LL],'r'); % 起始点
fill([qset(1,2)-LL,qset(1,2)+LL,qset(1,2)+LL,qset(1,2)-LL],[qset(2,2)-LL,qset(2,2)-LL,qset(2,2)+LL,qset(2,2)+LL],'b'); % 终点
% 创建随机路图
[V,G,Index_startInPRM,Index_endInPRM]=build_PRM(n,k,QLIST,MAX_X,MAX_Y,qset);
 
%% 1. 利用A star算法寻路
path = A_star_search( G, V, Index_startInPRM,Index_endInPRM );
repath = [];
repath = [repath;qset(:,1)'];
kk = size(path,1);
for i=1:size(path,1)
    repath = [repath;path(kk,:)];
    kk = kk-1;
end
repath = [repath;qset(:,2)'];
plot(repath(:,1)',repath(:,2)','m-','LineWidth',2)

可以看出相比源代码，不需要找起始点和终止点的函数[Index_startInPRM, Index_endInPRM] = findStartAndEndInPRM( V, qset, QLIST)了

3 改进代码运行效果

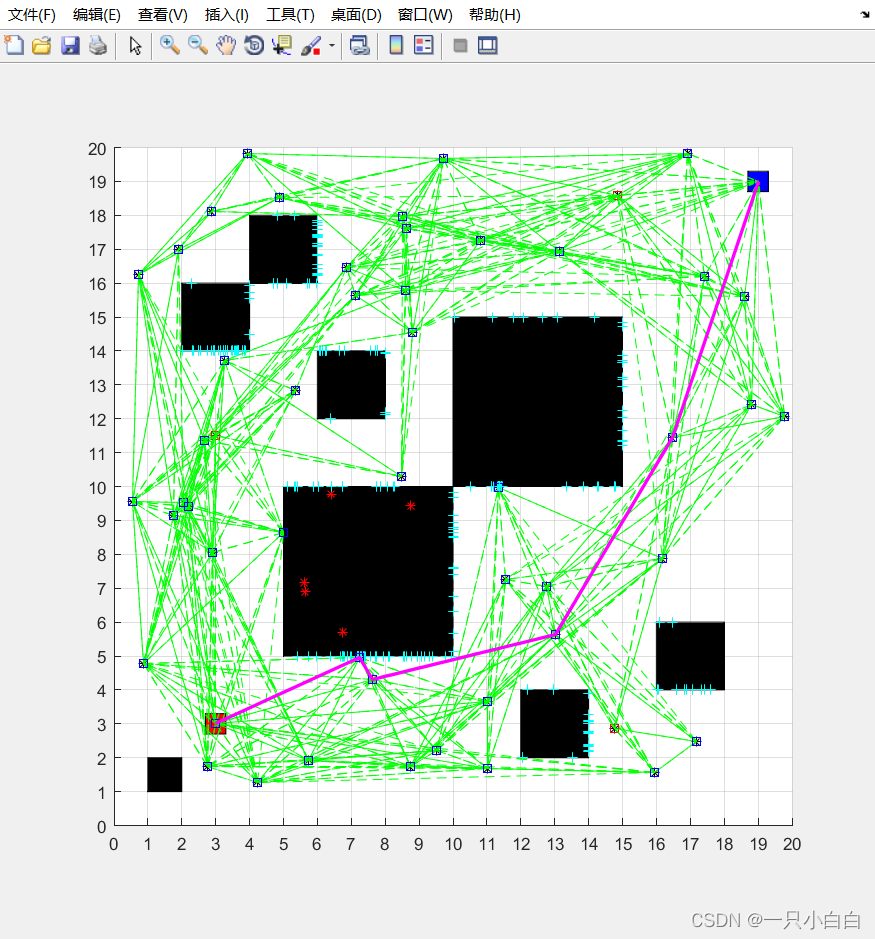
4 github链接

【github】移动机器人运动规划