斯坦福大学NLP课程CS224N课第一次作业第三部分（中）_stanford nlp课后作业答案

斯坦福大学NLP课程CS224N课第一次作业第三部分（中）

上一篇博客我们大体了解了word embedding原理和word2vec原理，这一节我们就开始实现word2vec，作业见q3_word2vec.py。

1. word2vec的softmax版本

我们在上篇博客其实实现了两种softmax方法，其中一种是基于softmax，一种是基于负采样。我们先实现softmax方法。
给的代码很长，但是下面大部分都是构建训练集，所以我们暂时不看那些，直接看需要补充的函数了。
首先是一个开胃小菜，让我们补充一个归一化函数，我们看一下函数：

def normalizeRows(x):
    """ Row normalization function

    Implement a function that normalizes each row of a matrix to have
    unit length.
    """

    ### YOUR CODE HERE
    raise NotImplementedError
    ### END YOUR CODE

    return x
1
2
3
4
5
6
7
8
9
10
11
12

然后我们看下面的测试函数：

def test_normalize_rows():
    print "Testing normalizeRows..."
    x = normalizeRows(np.array([[3.0,4.0],[1, 2]]))
    print x
    ans = np.array([[0.6,0.8],[0.4472136,0.89442719]])
    assert np.allclose(x, ans, rtol=1e-05, atol=1e-06)
    print ""
1
2
3
4
5
6
7
8

很显然是对行进行平方归一化，所以写起来很简单，一行搞定：

x = x/np.sqrt(np.sum(x*x,axis=1,keepdims=True))
1

然后我们可以可以看看我们需要实现的函数：

def softmaxCostAndGradient(predicted, target, outputVectors, dataset):
1

其中predicted是预测向量，target是待预测向量的序号（id），其中outputVectors是待预测向量矩阵，dataset暂时没用。
然后我们可以下面公式来实现正向传播和计算损失函数：


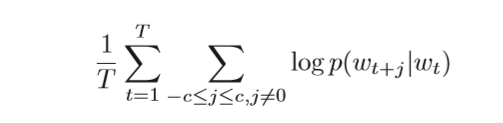
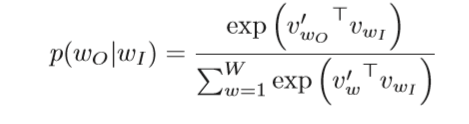
这个损失函数前面我们已经说了，是最大化相邻词的内积，因为我们后面会使用随机梯度下降，所以我们在前面加个负号，将最大化问题变成最小化问题。

predicted = predicted.reshape([1,predicted.shape[0]])
p = softmax(np.dot(predicted,outputVectors.T))
cost = -p[0][target]
1
2
3

这样损失函数和前向传播就已经求完了，因为这里的损失函数实质上就是待预测矩阵的所有向量乘以预测向量，然后求softmax，其中第target个softmax值就是我们需要优化的值。
而后向算法实质就是softmax求导问题，在之前的博客中涉及到这个，这里我再次推导一次：

写的比上一张博客的清晰多了，知道是为什么吗？因为我推完了又抄了一遍，上一张博客不想再抄了。
怎么检验我们写的对不对呢，答案很简单，梯度校验即可，我们实现以下，实现的方法有很多种，我代码能力不行，写的不好大家见谅：

def softmaxCostAndGradient(predicted, target, outputVectors, dataset):
'''
shape:
predicted: [n]
target:it is a num
outputVectors: [V,n]
dataset: not use
'''
	predicted = predicted.reshape([1,predicted.shape[0]])  #to [1,n]
    p = softmax(np.dot(predicted,outputVectors.T)) #[1,n][n,V]=[1,V]

    cost = -np.log(p[0][target])
    a = np.sum(np.exp(np.dot(predicted,outputVectors.T))) #a num
    gradPred = -outputVectors[target].reshape(predicted.shape)+\
               np.sum(np.exp(np.dot(predicted,outputVectors.T)).T*outputVectors,axis=0)/a
    grad = p.T*predicted #[V,1][1,n]=[V,n]
    grad[target] = -predicted+p[0][target]*predicted
    ### YOUR CODE HERE
    #raise NotImplementedError
    ### END YOUR CODE
    return cost, gradPred, grad
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

我这就是按照上面的推导写的，运行结果梯度校验没问题那就结果就没问题，如果有看不懂的欢迎留言。
然后负采样的方法我就不写了，大家如果需要我写的话那么就留言，我看到就会补充上。
我们看一下skip-gram这个函数：

def skipgram(currentWord, C, contextWords, tokens, inputVectors, outputVectors,
             dataset, word2vecCostAndGradient=softmaxCostAndGradient):
1
2

看这个函数的输入就有点烦，太多了。我再反复看输入输出之下终于弄懂了（就是不懂的输出各个参数）：currentWord就是当前的中心词，是一个string类型的数据，C在这个函数没什么用，就是窗口的意思，contextWord是相邻的词组成的list，里面的元素都是string，tokens是一个字典可以将string转化成id，id可以在矩阵中查找这个词是第几行的向量，inputVectors是中心词矩阵，outputVectors是周围词矩阵，word2vecCostAndGradient是选择softmax方法还是负采样方法，所以我们继承这个函数也比较简单：

def skipgram(currentWord, C, contextWords, tokens, inputVectors, outputVectors,
             dataset, word2vecCostAndGradient=softmaxCostAndGradient):
	cost = 0.0
    gradIn = np.zeros(inputVectors.shape)
    gradOut = np.zeros(outputVectors.shape)

    for word in contextWords:
        c,gradPred,grad = word2vecCostAndGradient(inputVectors[tokens[currentWord]],
                                                    tokens[word],
                                                    outputVectors,dataset)
        cost += c
        gradIn[tokens[currentWord], :] += np.squeeze([gradPred])
        gradOut += grad
        return cost, gradIn, gradOut
1
2
3
4
5
6
7
8
9
10
11
12
13
14

又不懂评论可以问，有问必答。
OK，我们相当于把q3_word2vec.py需要实现的部分的一半讲完了，另外一半需要自己推导一下，别忘了推导完用梯度校验检验它们对不对。
有问题可以评论交流，有问必答。
欢迎评论交流，也欢迎关注，会将CS224N的所有作业写成博客的。